We included HMH Into Math Grade 4 Answer Key PDF Module 15 Lesson 2 Rename Fractions and Mixed Numbers to make students experts in learning maths.
HMH Into Math Grade 4 Module 15 Lesson 2 Answer Key Rename Fractions and Mixed Numbers
I Can rename mixed numbers as a sum of fractions with like denominators.
Spark Your Learning
Monique runs around a \(\frac{1}{4}\)-mile track 9 times. How many whole miles and how many quarter miles does Monique run?

Use a visual representation and write an equation modeling the problem.
Answer:
2\(\frac{1}{4}\)
2 whole numbers and 1 quarter mile
Explanation:
Monique runs around a \(\frac{1}{4}\)-mile track 9 times
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
Total miles Monique run = \(\frac{9}{4}\)
= 2 \(\frac{1}{4}\)
Turn and Talk How would your fraction model and answer change if she ran 9 laps on a track that was a \(\frac{1}{8}\)-mile track?
Answer:
9 \(\frac{1}{8}\)
Explanation:
\(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) = \(\frac{72}{8}\) = 9 \(\frac{1}{8}\)
Build Understanding
Question 1.
Chad runs around the quarter-mile track for 1\(\frac{1}{4}\) miles. How many laps does Chad run?

How can you use the mixed number 1\(\frac{1}{4}\) to help you solve this problem?
Connect to Vocabulary
A mixed number is a number represented by a whole number and a fraction. A mixed number can be renamed as a fraction greater than 1.
Use a visual representation to help you solve the problem and then write an equation to model the problem.
Answer:
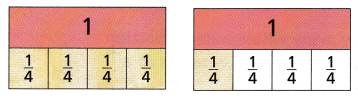
Explanation:
1 whole = 4 quarters
So, there is one whole numbers and one fourth of whole number.
= 1\(\frac{1}{4}\)
A. How did you decide how many sections to divide the whole into?
Answer:
4 section
![]()
Explanation:
1 whole = 4 quarters
So, one whole is divided into 4 sections.
B. How did you know how many parts to shade?
Answer:
5 parts
Explanation:
The quarter-mile track for 1\(\frac{1}{4}\) miles
So, total 5 laps and 5 parts
4 x \(\frac{1}{4}\) + \(\frac{1}{4}\) =1 \(\frac{1}{4}\)
C. How is your answer represented in your visual model?
Chad runs around the track _________ times.
Answer:
![]()
Chad runs around the track 5 times.
Explanation:
The quarter-mile track for 1\(\frac{1}{4}\) miles
So, total 5 laps and 5 parts
Step It Out
Question 2.
Puja ran around the \(\frac{1}{4}\)-mile track 15 times. Written as a mixed number, how many miles did Puja run?

A. Write a fraction greater than 1 to represent the number of miles Puja ran.
Answer:
\(\frac{15}{4}\)
Explanation:
Puja ran around the \(\frac{1}{4}\)-mile track 15 times.
As a mixed number we write = 15\(\frac{1}{4}\)
As a fraction = \(\frac{15}{4}\)
So, fraction is greater than 1 to represent the number of miles Puja ran.
B. What fraction with a denominator of 4 is equal to 1 whole?
Answer: 4
\(\frac{4}{4}\) = 1
Explanation:
1 whole = 4 quarters
So, 4 quarters with a denominator of 4 is equal to 1 whole.
C. Find the number of groups of \(\frac{4}{4}\) in \(\frac{15}{4}\). Determine how many fourths will be left over.
Answer:
\(\frac{3}{4}\)
Explanation:
\(\frac{4}{4}\) in \(\frac{15}{4}\) = 3 \(\frac{3}{4}\)
D. Write an equation modeling your answer to C.
Answer:
\(\frac{3}{4}\)
Explanation:
\(\frac{4}{4}\) in \(\frac{15}{4}\) = 3 \(\frac{3}{4}\)
E. Find how many whole miles Puja ran and what fraction of a mile is left. Then, write the number of miles as a mixed number.
Answer: 3
3\(\frac{3}{4}\)
Explanation:
\(\frac{4}{4}\) in \(\frac{15}{4}\) = 3 \(\frac{3}{4}\)
Turn and Talk What rule could you use to describe the relationship between the numerator and denominator to determine the number of wholes there are in a fraction greater than 1?
Answer:
A fraction has a numerator that is greater than or equal to the denominator,
then the fraction is an improper fraction.
An improper fraction is always 1 or greater than 1.
And, finally, a mixed number is a combination of a whole number and a proper fraction.
Check Understanding
Question 1.
Susan has 11 pieces of pizza. If each piece is \(\frac{1}{8}\) of a pizza, what mixed number describes how much pizza Susan has?
Answer:
11\(\frac{1}{8}\)
Explanation:
Susan has 11 pieces of pizza.
If each piece is \(\frac{1}{8}\) of a pizza,
In mixed number how much pizza Susan has = 11 x \(\frac{1}{8}\)
= \(\frac{89}{8}\)
Question 2.
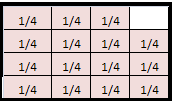
Nick needs 3\(\frac{3}{4}\) cups of flour. He only has a \(\frac{1}{4}\)-cup measuring cup. How many times will he fill the measuring cup?
Answer:
15 times
Explanation:
Nick needs 3\(\frac{3}{4}\) cups of flour.
He only has a \(\frac{1}{4}\)-cup measuring cup.
Number of times he fill the measuring cup
3\(\frac{3}{4}\) = \(\frac{15}{4}\)
On Your Own
Question 3.
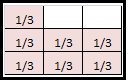
Nora needs 2\(\frac{1}{3}\) cups of milk for a recipe. She can only find a \(\frac{1}{3}\)-cup measuring cup. How many times will she fill the measuring cup?

Answer:
7 times
Explanation:
Nora needs 2\(\frac{1}{3}\) cups of milk for a recipe.
She can only find a \(\frac{1}{3}\)-cup measuring cup.
Number of times she fill the measuring cup
2\(\frac{1}{3}\) = \(\frac{7}{3}\)
Question 4.
Model with Mathematics Rename \(\frac{13}{6}\) as a mixed number. Draw a visual representation and write an equation to justify your answer.
Answer:
2 \(\frac{1}{6}\)
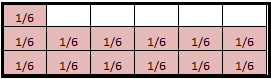
Explanation:
1 whole = 4quarters
\(\frac{13}{6}\) = 2 \(\frac{1}{6}\)
Question 5.
Write the quantity represented by the fraction model as a fraction, as a mixed number, and as a sum of fractions that are equal to 1 or less.

Answer:
2 \(\frac{1}{4}\) = \(\frac{9}{4}\)
Explanation:
1 whole = 4 quarters
There are 2 sets of wholes and 1 quarter.
So, the quantity represented by the fraction model as a fraction = \(\frac{9}{4}\)
As a mixed number = 2\(\frac{1}{4}\)
Write the mixed number as a fraction.
Question 6.
4\(\frac{3}{6}\) = __________
Answer:
\(\frac{27}{6}\)
Explanation:
First multiply the whole number with the denominator of the proper fraction.
Add the numerator of the proper fraction to this product.
= 4\(\frac{3}{6}\)
= \(\frac{3+24}{6}\)
= \(\frac{27}{6}\)
Question 7.
2\(\frac{5}{8}\) = ___________
Answer:
\(\frac{21}{8}\)
Explanation:
First multiply the whole number with the denominator of the proper fraction.
Add the numerator of the proper fraction to this product.
= 2\(\frac{5}{8}\)
= \(\frac{16+5}{8}\)
= \(\frac{21}{8}\)
Write the fraction as a mixed number.
Question 8.
\(\frac{36}{10}\) = ___________
Answer:
3\(\frac{6}{10}\)
Explanation:
Divide the numerator by the denominator.
Write down the whole number part of the quotient.
Write the remainder as numerator.
\(\frac{36}{10}\) = 3\(\frac{6}{10}\)
Question 9.
\(\frac{19}{6}\) = _________
Answer:
3\(\frac{1}{6}\)
Explanation:
Divide the numerator by the denominator.
Write down the whole number part of the quotient.
Write the remainder as numerator.
\(\frac{19}{6}\) = 3\(\frac{1}{6}\)
I’m in a Learning Mindset!
How did sharing strategies help me rename fractions as mixed numbers?
Answer:
Mixed number is a number which are represented by a whole number and a fraction.
Factions greater than 1 have numerators that are greater than their denominators are known as improper fractions.
Explanation:
By using the strategies number lines or fraction strips.
Renaming a mixed number as an improper fraction means to convert into equivalent fractions.