We included HMH Into Math Grade 4 Answer Key PDF Module 15 Lesson 1 Add and Subtract Fractions to Solve Problems to make students experts in learning maths.
HMH Into Math Grade 4 Module 15 Lesson 1 Answer Key Add and Subtract Fractions to Solve Problems
I Can add and subtract fractions greater than one with like denominators to solve real-world problems.
Spark Your Learning
Mrs. Hanson needs 9 servings of almonds. Each serving weighs \(\frac{1}{4}\) pound. She already has \(\frac{3}{4}\) pound of almonds. How many more pounds of almonds does she need?

Draw a fraction model to help you solve the problem.
Answer:
![]()
Almonds already has = \(\frac{3}{4}\)
Almonds needed = \(\frac{6}{4}\)
Explanation:
Mrs. Hanson needs 9 servings of almonds.
Each serving weighs \(\frac{1}{4}\) pounds.
Already he has \(\frac{3}{4}\) pounds of almonds.
Total Almonds he needed = \(\frac{9}{4}\) – \(\frac{3}{4}\)
= \(\frac{6}{4}\) pounds.
Turn and Talk One classmate represents this problem with an addition equation and another uses a subtraction equation. Who is correct and how do you know?
Answer:
Both are correct.
Explanation:
Addition and subtractions are inverse to each other,
that means we can undo an addition through subtraction,
and we can undo a subtraction through addition.
Addition equation \(\frac{3}{4}\) + \(\frac{6}{4}\) = \(\frac{9}{4}\)
Subtraction equation \(\frac{9}{4}\) – \(\frac{3}{4}\) = \(\frac{6}{4}\)
Build Understanding
Question 1.
Brooke and Bailey each bring \(\frac{1}{4}\)-pound bowls of grapes to serve at a class party. This shows the number of bowls each person brings. How many pounds of grapes do they bring?

Show how you could find the total amount.
Answer:
\(\frac{7}{4}\)
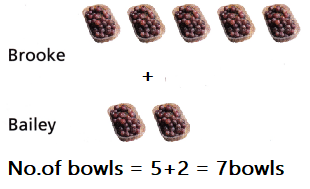
A. What does a unit fraction represent in the problem?
Answer:
Unit fraction is \(\frac{1}{4}\)
B. What addition equation models the problem?
Answer:
\(\frac{5}{4}\) + \(\frac{2}{4}\)
C. How many bowls of grapes do Brooke and Bailey bring?
Answer:
7 bowls
D. What is the weight of the grapes the two students bring?
Answer:
\(\frac{7}{4}\)
Explanation:
Brooke brings 5 bowls of \(\frac{1}{4}\) pounds of grapes = \(\frac{5}{4}\)
Bailey brings 2 bowls of \(\frac{1}{4}\) pounds of grapes = \(\frac{2}{4}\)
Total pounds of grapes = \(\frac{5}{4}\) + \(\frac{2}{4}\)
= \(\frac{7}{4}\) pounds of grapes.
Step It Out
Question 2.
Mrs. Hanson makes a snack mix with this bag of raisins and this box of cereal. The students eat \(\frac{14}{12}\) pounds of snack mix at the party. How much snack mix is left?

A. How can you find the weight of the snack mix Mrs. Hanson makes?
Answer:
By adding both the weights of Cereal and Raisins mix.
B. Model this part of the problem with an equation and find how much snack mix Mrs. Hanson makes.
Answer:
\(\frac{8}{12}\) + \(\frac{9}{12}\)
C. How can you find how much is left after the students eat some?
Answer:
By subtracting the eaten portion from the total snack mix.
D. Model this part of the problem with an equation and find how much snack mix is left.
Answer:
\(\frac{17}{12}\) – \(\frac{14}{12}\) = \(\frac{3}{12}\)
Explanation:
Weight of Raisins is \(\frac{8}{12}\)
Weight of Cereals is \(\frac{9}{12}\)
total weight of snack mix = \(\frac{8}{12}\) + \(\frac{9}{12}\)
= \(\frac{17}{12}\)
The students eat \(\frac{14}{12}\) pounds of snack mix at the party.
Snack mix is left = \(\frac{17}{12}\) – \(\frac{14}{12}\)pounds
= \(\frac{3}{12}\) pounds
Turn and Talk In terms of the snack mix, what does it mean for the amount of snack mix Mrs. Hanson makes to be described as a fraction greater than 1?
Answer:
\(\frac{17}{12}\)
Explanation:
When the numerator is greater than denominator than we express the fraction as greater than 1.
Check Understanding
Question 1.
Delia has \(\frac{4}{10}\) yard of white ribbon and \(\frac{8}{10}\) yard of red ribbon. How many yards of ribbon does she have?
Answer:
\(\frac{12}{10}\) yards of ribbon.
Explanation:
Delia has \(\frac{4}{10}\) yard of white ribbon,
\(\frac{8}{10}\) yard of red ribbon.
Total yards of ribbon she have = \(\frac{4}{10}\) + \(\frac{8}{10}\)
= \(\frac{12}{10}\) yards ribbon.
Question 2.
Frankie has \(\frac{3}{8}\) pound of sunflower seeds and \(\frac{7}{8}\) pound of cracked corn that he mixes together for bird feed. He puts \(\frac{9}{8}\) pounds in a bird feeder. How many pounds does he have now?
Answer:
\(\frac{1}{8}\) pounds
Explanation:
Frankie has \(\frac{3}{8}\) pound of sunflower seeds,
\(\frac{7}{8}\) pound of cracked corn that he mixes together for bird feed.
= \(\frac{3}{8}\) + \(\frac{7}{8}\) = \(\frac{10}{8}\)
He puts \(\frac{9}{8}\) pounds in a bird feeder.
Total pounds he have now = \(\frac{10}{8}\) – \(\frac{9}{8}\)
= \(\frac{1}{8}\) pounds
On Your Own
Question 3.
Reason Brad has some water in a bucket. He pours \(\frac{3}{10}\) liter of water on some house plants. Now there is \(\frac{4}{10}\) liter of water in the bucket. How many liters of water did Brad have in the bucket before watering the plants? Show your work.
Answer:
\(\frac{7}{10}\) liters
Explanation:
Brad pours \(\frac{3}{10}\) liter of water on some house plants.
Now there is \(\frac{4}{10}\) liter of water in the bucket.
Total liters of water Brad have in the bucket before watering the plants
= \(\frac{3}{10}\) + \(\frac{4}{10}\)
= \(\frac{3+4}{10}\) = \(\frac{7}{10}\)
Question 4.
Use Tools Lily spends \(\frac{3}{5}\) hour reading, \(\frac{2}{5}\) hour helping her mother, and \(\frac{1}{5}\) hour playing with her little brother. How many hours does Lily spend on these tasks? Make a visual fraction model to represent the problem.
Answer:
Lily spends \(\frac{6}{5}\) hours.

Explanation:
Lily spends \(\frac{3}{5}\) hour reading,
\(\frac{2}{5}\) hour helping her mother,
and \(\frac{1}{5}\) hour playing with her little brother.
Total hours Lily spend on these tasks
= \(\frac{3}{5}\) + \(\frac{2}{5}\) + \(\frac{1}{5}\)
= \(\frac{3+2+1}{5}\) = \(\frac{6}{5}\)
Question 5.
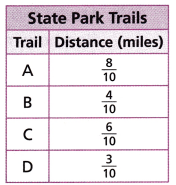
A state park has 4 trails that are less than 1 mile in length. Spencer wants to walk more than \(\frac{15}{10}\) miles, but less than \(\frac{19}{10}\) miles. Which trails could he walk? Justify your response.
Answer:
Trail C \(\frac{4}{10}\) miles.
Explanation:
A state park has 4 trails that are less than 1 mile in length.
Spencer wants to walk more than \(\frac{15}{10}\) miles,
but less than \(\frac{19}{10}\) miles.
Preferable trails he could walk = \(\frac{19}{10}\) – \(\frac{15}{10}\)
= \(\frac{4}{10}\) miles on trail C.
Find the sum or difference.
Question 6.
\(\frac{3}{6}\) + \(\frac{7}{6}\) = ___________
Answer:
\(\frac{10}{6}\) = \(\frac{5}{3}\)
Explanation:
\(\frac{3}{6}\) + \(\frac{7}{6}\) = \(\frac{3+7}{6}\)
= \(\frac{10}{6}\) = \(\frac{5}{3}\)
Question 7.
\(\frac{11}{10}\) – \(\frac{3}{10}\) = __________
Answer:
\(\frac{8}{10}\) = \(\frac{4}{5}\)
Explanation:
\(\frac{11}{10}\) – \(\frac{3}{10}\) = \(\frac{11- 3}{10}\)
= \(\frac{8}{10}\) = \(\frac{4}{5}\)
Question 8.
\(\frac{2}{4}\) + \(\frac{3}{4}\) – \(\frac{1}{4}\) = __________
Answer:
\(\frac{4}{4}\) = 1
Explanation:
\(\frac{2}{4}\) + \(\frac{3}{4}\) – \(\frac{1}{4}\)
= \(\frac{2+3-1}{4}\) = \(\frac{5 – 1}{4}\)
= \(\frac{4}{4}\) = 1
Question 9.
\(\frac{8}{12}\) + \(\frac{6}{12}\) + \(\frac{5}{12}\) = ___________
Answer:
\(\frac{19}{12}\)
Explanation:
\(\frac{8}{12}\) + \(\frac{6}{12}\) + \(\frac{5}{12}\)
= \(\frac{8+6+5}{12}\) = \(\frac{19}{12}\)
I’m in a Learning Mindset!
What strategy worked best for me when solving these problems?
Answer:
Combined operations of addition and subtractions.
Explanation:
Combined operations refers to problems where you need to do more than one operation,
like addition and subtraction.