We included HMH Into Math Grade 4 Answer Key PDF Module 14 Lesson 6 Add Fractional Parts of 10 and 100 to make students experts in learning maths.
HMH Into Math Grade 4 Module 14 Lesson 6 Answer Key Add Fractional Parts of 10 and 100
I Can rename fractions with denominators of 10 and 100 so both have denominators of 100. I can add the fractions.
Step It Out
Question 1.
A cook measures the mass of salt and puts it in a bowl. Then she measures the mass of pepper and puts it in the same bowl. What is the mass of the salt and pepper mixture?

You can add two fractions if they have the same denominator. When fractions have the same denominator, they have a common denominator. The fractions \(\frac{4}{10}\) and \(\frac{25}{100}\) do not have a common denominator.
Connect to Vocabulary
A common denominator is a denominator that two or more fractions share.
Example: \(\frac{5}{8}\), \(\frac{2}{8}\)
A. You can always rename a fraction with a denominator of 10 as an equivalent fraction with a denominator of 100.
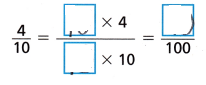
Answer:
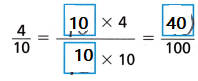
B. Now you can add the fractions.
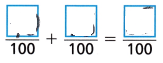
Answer:
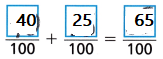
C. What is the mass of the salt and pepper mixture?
Answer:
\(\frac{65}{100}\)
Explanation:
Mass of salt \(\frac{4}{10}\) and mass of pepper \(\frac{25}{100}\)
Make the fraction of mass as equivalent fractions by multiplying the numerator and denominator with 10.
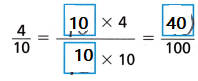
Then add the both the masses to find the sum.
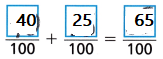
Step It Out
Question 2.
A wallaby jumps \(\frac{7}{10}\) meter. Then it jumps \(\frac{18}{100}\) meter. How far does the wallaby jump after jumping twice?

A. Write an equation to model the problem. Use j for the distance the wallaby jumps after jumping twice.
Answer:
j = \(\frac{7}{10}\) + \(\frac{18}{100}\)
B. Rename \(\frac{7}{10}\) as a fraction with a denominator of 100.
\(\frac{7}{10}\) = ____________
Answer:
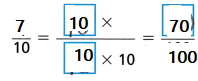
C. Find the value of j.
Answer:
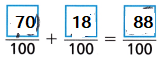
D. How far does the wallaby jump after jumping twice?
Answer:
\(\frac{88}{100}\)
Explanation:
A wallaby jumps \(\frac{7}{10}\) meter.
Then it jumps \(\frac{18}{100}\) meter.
Total jump after jumping twice = \(\frac{88}{100}\) meter.
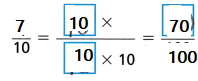
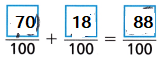
Turn and Talk Why can you always rename a tenth as a hundredth?
Answer:
When the fractions have the denominators as tenth and hundredth than multiply the number of tenths by 10 to convert to hundredths,
to equalize the denominators of both the fractions.
Check Understanding
Question 1.
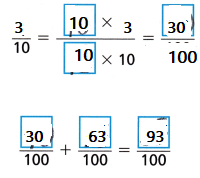
Molly has \(\frac{3}{10}\) pound of red clay and \(\frac{63}{100}\) pound of gray clay. How many pounds of clay does she have?
Answer:
\(\frac{93}{100}\) pounds
Explanation:
Molly has \(\frac{3}{10}\) pound of red clay and
\(\frac{63}{100}\) pound of gray clay.
Total pounds of clay she have,
Find the sum.
Question 2.
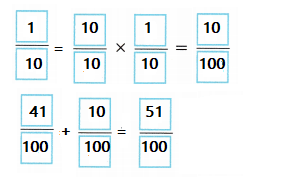
\(\frac{41}{100}\) + \(\frac{1}{10}\) = ___________
Answer:
\(\frac{51}{100}\)
Explanation:
Equalize the denominators on both sides, and then add.
Question 3.
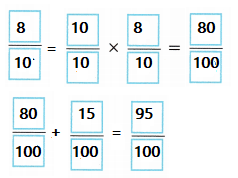
\(\frac{8}{10}\) + \(\frac{15}{100}\) = ___________
Answer:
\(\frac{95}{100}\)
Explanation:
Equalize the denominators on both sides, and then add.
Question 4.
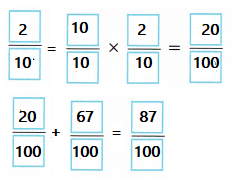
\(\frac{2}{10}\) + \(\frac{67}{100}\) = ___________
Answer:
\(\frac{87}{100}\)
Explanation:
Equalize the denominators on both sides, and then add.
Question 5.
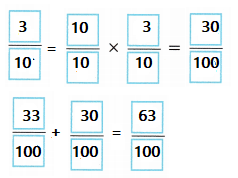
\(\frac{33}{100}\) + \(\frac{3}{10}\) = ___________
Answer:
\(\frac{63}{100}\)
Explanation:
Equalize the denominators on both sides, and then add.
On Your Own
Question 6.
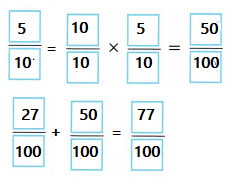
Attend to Precision Daniel collects rocks. What is the total mass of the piece of quartz and the piece of obsidian?

You can use the hundredths model to help you rename \(\frac{5}{10}\) as a fraction with a denominator of 100.
Model the problem with an equation. Let m = the total mass of the two rocks. Then find the value of m.
Answer:
m = \(\frac{77}{100}\)
Explanation:
mass of quartz = \(\frac{27}{100}\)
mass of obsidian = \(\frac{5}{10}\)
m = total mass of the two rocks
Question 7.
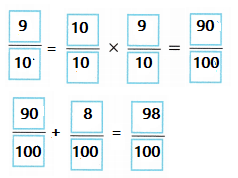
Model with Mathematics Keisha pours \(\frac{9}{10}\) liter of orange juice into a jug. Then she pours \(\frac{8}{100}\) liter of lemon juice into the jug. How much juice is in the jug?
Use multiplication to rename \(\frac{9}{10}\) as a fraction with a denominator of 100. Model the problem with an equation. Let j = the amount of juice in the jug. Then find the value of j.
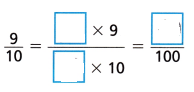
Answer:
j = \(\frac{98}{100}\)
Explanation:
Keisha pours \(\frac{9}{10}\) liter of orange juice into a jug.
Then she pours \(\frac{8}{100}\) liter of lemon juice into the jug.
Total juice is in the jug
Question 8.
Construct Arguments A balloon is \(\frac{13}{100}\) kilometer above ground. Some wind takes the balloon \(\frac{4}{10}\) kilometer higher. How far above the ground is the balloon now? How do you know your answer is reasonable?
Answer:
\(\frac{53}{100}\)
Explanation:
A balloon is \(\frac{13}{100}\) kilometer above ground.
Some wind takes the balloon \(\frac{4}{10}\) kilometer higher.
Distance above the ground in the balloon is
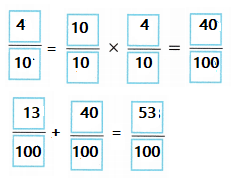
Find the sum.
Question 9.
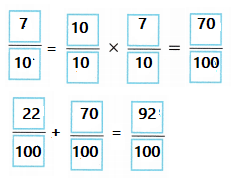
\(\frac{22}{100}\) + \(\frac{7}{10}\) = __________
Answer:
\(\frac{92}{100}\)
Explanation:
Question 10.
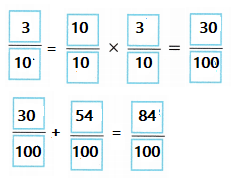
\(\frac{3}{10}\) + \(\frac{54}{100}\) = ___________
Answer:
\(\frac{84}{100}\)
Explanation:
Question 11.
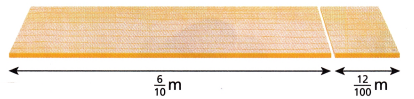
Theo lays two boards on the ground. What is the total length of the boards?
Answer:
\(\frac{72}{100}\)
Explanation:
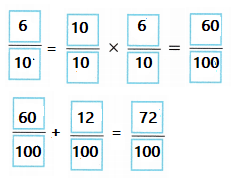
Length of the two boards on the ground are \(\frac{6}{10}\) and \(\frac{12}{100}\)
Total length of the boards are \(\frac{72}{100}\)
Question 12.
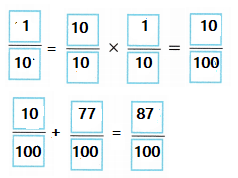
STEM Water accounts for \(\frac{77}{100}\) of the average brain’s weight, protein accounts for \(\frac{8}{100}\) of the weight, and fat accounts for \(\frac{1}{10}\) of the weight. What part of the weight of an average is made up of water and fat combined?
Answer:
\(\frac{87}{100}\)
Explanation:
Water accounts for \(\frac{77}{100}\) of the average brain’s weight,
fat accounts for \(\frac{1}{10}\) of the weight.
combined part of the weight of an average is made up of water and fat
Question 13.
Reason Olivia needs to empty three of the beakers below into a jar that holds \(\frac{3}{4}\) liter. Circle the three beakers that Olivia should empty into the jar.
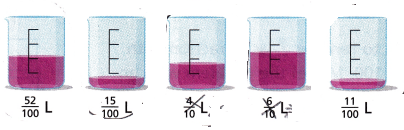
Explain how you chose the right beakers.
Answer:
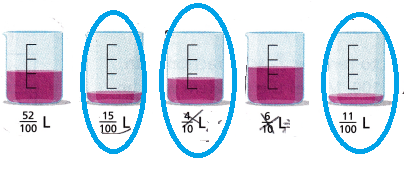
Explanation:
Olivia needs to empty three of the beakers, if he empty the jars of \(\frac{15}{100}\) liter, \(\frac{4}{10}\) liter and \(\frac{11}{100}\) liter it equal to \(\frac{3}{4}\) liter.
\(\frac{3}{4}\) liter x \(\frac{25}{25}\) liter = \(\frac{75}{100}\) liter
Find the sum.
Question 14.
\(\frac{8}{10}\) + \(\frac{4}{100}\) = __________
Answer:
\(\frac{84}{100}\)
Explanation:
Equalize the denominators on both sides.
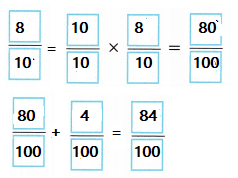
Question 15.
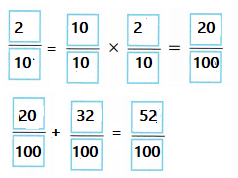
\(\frac{32}{100}\) + \(\frac{2}{10}\) = ___________
Answer:
\(\frac{52}{100}\)
Explanation:
Equalize the denominators on both sides.