We included HMH Into Math Grade 4 Answer Key PDF Module 14 Lesson 5 Represent Subtraction of Fractions to make students experts in learning maths.
HMH Into Math Grade 4 Module 14 Lesson 5 Answer Key Represent Subtraction of Fractions
I Can write equations and find the difference of fractions with like denominators.
Spark Your Learning
Marcy and Lindsey are playing games at a local carnival. They play the game “Measure Your Strength,” and their results are shown. Find how much farther Marcy hits the puck up the board than Lindsey.
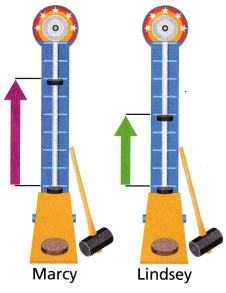
Show your thinking.
Answer:
\(\frac{2}{8}\) farther Marcy hits the puck up the board than Lindsey.
Explanation:
Equation model can be written to find the difference of fractions with like denominators as shown below,
for the above game to measure the strengths between the Marcy and Lindsey.
out of 8 points Marcy strength is measured as 6 points = \(\frac{6}{8}\)
out of 8 points Marcy strength is measured as 4 points = \(\frac{4}{8}\)
Difference = \(\frac{6}{8}\) – \(\frac{4}{8}\)
= \(\frac{2}{8}\) farther Marcy hits the puck up the board than Lindsey.
Turn and Talk Compare your work with a classmate. Did you get the same answer? Did you use the same method to solve the problem?
Answer:
Yes, I got the same answer as my friend.
Explanation:
out of 8 points Marcy strength is measured as 6 points = \(\frac{6}{8}\)
out of 8 points Marcy strength is measured as 4 points = \(\frac{4}{8}\)
Difference = \(\frac{6}{8}\) – \(\frac{4}{8}\)
\(\frac{2}{8}\) farther Marcy hits the puck up the board than Lindsey.
Build Understanding
Question 1.
Leo checked the levels of grape drink in this cooler before and after lunch. How much grape drink was used during lunch? The cooler holds 1 gallon.
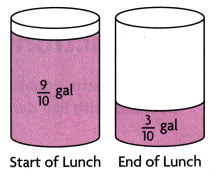
Use a visual fraction model to represent the problem and find the solution.
A. How did you represent the starting amount of grape drink on your fraction model?
Answer:
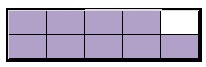
starting amount of grape drink on fraction model is \(\frac{9}{10}\)
B. How did you represent the amount of drink that was consumed on your fraction model?
Answer:
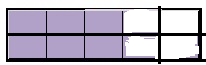
The amount of drink that was consumed on fraction model \(\frac{6}{10}\)
C. What represents the solution on your fraction model?
Answer:
Difference = \(\frac{9}{10}\) – \(\frac{6}{10}\)
= \(\frac{3}{10}\)
D. Write an equation to model the problem.
Answer:
An equation to model the problem is as follows,
= \(\frac{9}{10}\) – \(\frac{6}{10}\)
= \(\frac{3}{10}\)
E. How much of the grape drink was used during lunch?
Answer:
\(\frac{6}{10}\) the amount of drink that was consumed during lunch.
Explanation:
Before lunch Leo has \(\frac{9}{10}\) gallon of grape juice.
After lunch Leo has \(\frac{3}{10}\) gallon of grape juice.
The amount of drink that was consumed during lunch
= \(\frac{9}{10}\) – \(\frac{6}{10}\)
= \(\frac{3}{10}\)
Step It Out
Question 2.
Ross makes popcorn at a carnival. At the start of his shift, the container of kernels weighs \(\frac{11}{12}\) pound. During his shift, he uses \(\frac{3}{12}\) pound of the kernels. How many pounds of kernels are left after Ross’s shift?

You can write an equation without first making a visual fraction model.
A. Write an equation to model the situation. Use p for the weight of kernels left after Ross’s shift.
Answer:
\(\frac{8}{12}\)
Explanation:
p = \(\frac{11}{12}\) – \(\frac{3}{12}\)
p = \(\frac{8}{12}\)
B. Draw a visual fraction model to solve the problem.
Answer:
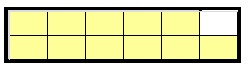
At the start of his shift, the container of kernels weighs
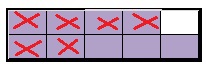
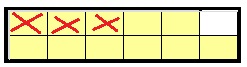
During his shift, he uses, red cross marked
C. How many pounds of kernels are left after Ross’s shift?
Answer:
p = \(\frac{8}{12}\) pounds left
Explanation:
At the start of his shift, the container of kernels weighs \(\frac{11}{12}\) pound.
During his shift, he uses \(\frac{3}{12}\) pound of the kernels.
Total pounds of kernels left after Ross’s shift
p = \(\frac{11}{12}\) – \(\frac{3}{12}\)
p = \(\frac{8}{12}\)
Check Understanding
Question 1.
Dee went fishing for \(\frac{3}{6}\) hour on Monday and \(\frac{2}{6}\) hour on Tuesday. How much longer did she fish on Monday than on Tuesday? Use the number lines to write an equation and solve the problem.
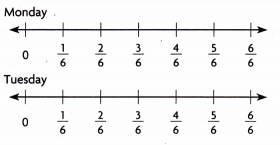
Answer:
\(\frac{1}{6}\) hour longer on Monday than Tuesday.
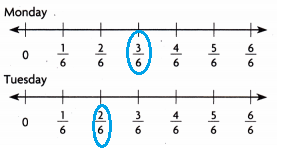
Explanation:
Dee went fishing for \(\frac{3}{6}\) hour on Monday and
\(\frac{2}{6}\) hour on Tuesday.
How much longer did she fish on Monday than on Tuesday
\(\frac{3}{6}\) – \(\frac{3}{6}\) = \(\frac{1}{6}\)
Find the difference.
Question 2.
\(\frac{7}{8}\) – \(\frac{1}{8}\) = __________
Answer:
\(\frac{6}{8}\)
Explanation:
Whole is divided into 8 equal parts.
Difference between fractions of whole
\(\frac{7}{8}\) – \(\frac{1}{8}\) = \(\frac{6}{8}\)
Question 3.
\(\frac{4}{6}\) – \(\frac{2}{6}\) = ___________
Answer:
\(\frac{2}{6}\)
Explanation:
Whole is divided into 6 equal parts.
Difference between fractions of whole
\(\frac{4}{6}\) – \(\frac{2}{6}\) = \(\frac{2}{6}\)
On Your Own
Question 4.
Use Reasoning Casey played \(\frac{6}{10}\) hour in one basketball game and \(\frac{2}{10}\) hour in the next game. How much longer did he play in the first game than the second game? Model the problem with an equation.
Answer:
\(\frac{4}{10}\) hours
Explanation:
Whole is divided into 10 equal parts.
Casey played \(\frac{6}{10}\) hour in one basketball game and
\(\frac{2}{10}\) hour in the next game.
Number of hours he played more in the first game than the second game
\(\frac{6}{10}\) – \(\frac{2}{10}\) = \(\frac{4}{8}\)
Question 5.
Model with Mathematics The water in a rain barrel was \(\frac{3}{8}\) inch deep. After a rain shower, the depth increased \(\frac{1}{8}\) inch. The level of water went down \(\frac{2}{8}\) inch after Jerry used water from the rain barrel to water plants. What is the depth of the water in the rain barrel now? Model the problem with equations.

Answer:
\(\frac{2}{8}\)
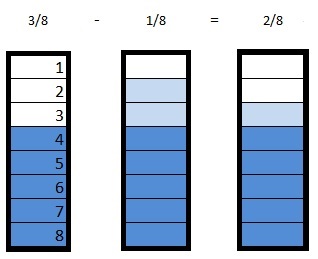
before rain, after rain shower, after water to plants
Explanation:
The water in a rain barrel was \(\frac{3}{8}\) inch deep.
After a rain shower, the depth increased \(\frac{1}{8}\) inch.
Level of water went down \(\frac{2}{8}\) inch after Jerry used water from the rain barrel to water plants. The depth of the water in the rain barrel now
\(\frac{3}{8}\) – \(\frac{1}{8}\) = \(\frac{2}{8}\)
Question 6.
Model with Mathematics Oliver has a board that is \(\frac{10}{12}\) foot long. After he cuts some off, he has \(\frac{7}{12}\) foot left. How much did Oliver cut off? Model the problem with an equation. Use b for the length of board Oliver cut off.
Answer:
\(\frac{3}{12}\)
Explanation:
Oliver has a board that is \(\frac{10}{12}\) foot long.
After he cuts some off, he has \(\frac{7}{12}\) foot left.
Total length Oliver cut off from board = \(\frac{10}{12}\) – \(\frac{7}{12}\)
= \(\frac{3}{12}\)
Find the difference.
Question 7.
\(\frac{9}{12}\) – \(\frac{3}{12}\) = __________
Answer:
\(\frac{6}{12}\)
Explanation:
Whole is divided into 12 equal parts.
Difference between fractions of whole
\(\frac{9}{12}\) – \(\frac{3}{12}\) = \(\frac{6}{12}\)
Question 8.
\(\frac{7}{10}\) – \(\frac{4}{10}\) = __________
Answer:
\(\frac{3}{10}\)
Explanation:
Whole is divided into 10 equal parts.
Difference between fractions of whole
\(\frac{7}{10}\) – \(\frac{4}{10}\) = \(\frac{3}{10}\)
Question 9.
\(\frac{4}{6}\) – \(\frac{1}{6}\) = __________
Answer:
\(\frac{3}{6}\)
Explanation:
Whole is divided into 6 equal parts.
Difference between fractions of whole
\(\frac{4}{6}\) – \(\frac{1}{6}\) = \(\frac{3}{6}\)
Question 10.
\(\frac{7}{8}\) – \(\frac{6}{8}\) = __________
Answer:
\(\frac{1}{8}\)
Explanation:
Whole is divided into 8 equal parts.
Difference between fractions of whole
\(\frac{7}{8}\) – \(\frac{6}{8}\) = \(\frac{1}{8}\)
I’m in a Learning Mindset!
What tools can I use to help me solve problems involving the subtraction of fractions?
Answer:
Fraction strips, Fraction models and number lines.
Explanation:
Make sure that the denominators of fractions should be same, than add or subtract the numerators.
Simplify the fraction if possible.