We included HMH Into Math Grade 4 Answer Key PDF Module 14 Lesson 4 Separate Parts of the Same Whole to make students experts in learning maths.
HMH Into Math Grade 4 Module 14 Lesson 4 Answer Key Separate Parts of the Same Whole
I Can show subtraction of fractions with visual models and use words to describe the difference.
Spark Your Learning
Ruby cuts off part of this piece of wood for a craft. How much of the original piece of wood does she now have for another project?
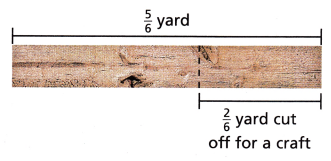
How can you represent this scenario using a visual model?
Show your thinking.
Answer:
\(\frac{3}{6}\)
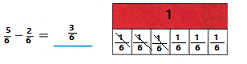
Explanation:
Ruby has \(\frac{5}{6}\) yards of a wood piece.
she cuts \(\frac{2}{6}\) yard of the wood piece.
Therefore, it will be \(\frac{5}{6}\) – \(\frac{2}{6}\)
That is \(\frac{5-2}{6}\)
That is \(\frac{3}{6}\)
Turn and Talk What operation did you represent with your visual model? What other operations could you have used?
Answer:
Subtraction operation:
Explanation:
Subtraction is the operation of taking the difference of two numbers.
Build Understanding
Question 1.
Ruby has \(\frac{9}{12}\) yard of red ribbon. She needs a piece that is \(\frac{2}{12}\) yard long to twist across a board. If Ruby cuts off what she needs, how much ribbon will she have for another project?

Use a fraction model to represent and solve the problem.
Answer:
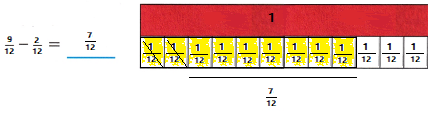
A. How does your fraction model represent the change in length?
Answer:
change in length = \(\frac{2}{12}\)
Explanation :

\(\frac{9}{12}\) – \(\frac{2}{12}\) = \(\frac{7}{12}\)
B. How does your fraction model represent the remaining length?
Answer:
remaining length = \(\frac{7}{12}\)
Explanation :

\(\frac{9}{12}\) – \(\frac{2}{12}\) = \(\frac{7}{12}\)
C. How long will the leftover ribbon be?
Answer:
\(\frac{7}{12}\) yard of ribbon
Explanation:
Ruby has \(\frac{9}{12}\) yard of ribbon
She cuts \(\frac{2}{12}\) yard of ribbon
therefore, it is \(\frac{9-2}{12}\)
so she now has \(\frac{7}{12}\) yard of ribbon
Turn and Talk How does the way you use a fraction model for adding fractions compare to the way you use a fraction model for subtracting fractions?
Answer:
Addition operation is opposite to subtraction operation;
Explanation:
In addition tow or more addends are added together to find the sum.
In subtraction we take the difference of two numbers.
Step It Out
Question 2.
Ruby has \(\frac{2}{3}\) yard of string. She only needs \(\frac{1}{3}\) yard to tie a knot. How much string will Ruby have after she cuts off \(\frac{1}{3}\) yard?

A. Write an equation to model the situation. Use “S” for the amount of string left.
Answer:
S = \(\frac{1}{3}\) yard
B. Use a fraction model to represent the amount of string Ruby has. Change your fraction model to represent the amount of string she uses to tie a knot. Draw a visual representation of how you found your solution.
Answer:
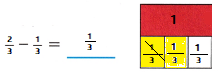
Explanation
the yellow part represents the string ruby has
thus when we remove on third of string we have one third of string remaining
C. How much string does Ruby have left?
Answer:
\(\frac{1}{3}\)
Explanation:
Ruby has \(\frac{2}{3}\) yard of string with her
She needs \(\frac{1}{3}\) yard to tie a knot
Therefore she cuts \(\frac{1}{3}\) yard of string from the string
Therefore, she has \(\frac{2-1}{3}\)
Simplifying this, we get, \(\frac{1}{3}\)
Therefore, S= \(\frac{1}{3}\)
Check Understanding
Question 1.
Michael had \(\frac{3}{4}\) cup of flour. He used \(\frac{2}{4}\) cup in a recipe. How much flour does Michael have now? Draw a fraction model to solve.
Answer:
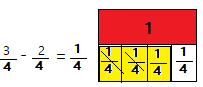
Explanation:
Michael had \(\frac{3}{4}\) cup of flour.
He used \(\frac{2}{4}\) cup in a recipe.
Total flour left with Michael now
\(\frac{3}{4}\) – \(\frac{2}{4}\) = \(\frac{1}{4}\)
Question 2.
Brynn has \(\frac{5}{10}\) of a book left to read. She reads \(\frac{2}{10}\) more of the book. How much does Brynn have left to read now?
Answer:
\(\frac{3}{10}\)
Explanation:
Brynn has \(\frac{5}{10}\) of a book left to read.
She reads \(\frac{2}{10}\) more of the book.
Total book left to read now = \(\frac{5}{10}\) – \(\frac{2}{10}\) = \(\frac{3}{10}\)
On Your Own
Question 3.
Use Tools Pedro has \(\frac{5}{8}\) gallon of water in a gallon jug. He pours \(\frac{2}{8}\) gallon of water from the jug into a water bottle. How much water does Pedro have in the jug now? Use a visual fraction model as a tool to support your answer to the problem.

Answer:

Explanation:
Pedro has \(\frac{5}{8}\) gallon of water in a gallon jug.
He pours \(\frac{2}{8}\) gallon of water from the jug into a water bottle.
Total water left in the jug now = \(\frac{5}{8}\) – \(\frac{2}{8}\) = \(\frac{3}{8}\)
Question 4.
Open Ended Write a word problem for the equation \(\frac{7}{12}\) – _______ = \(\frac{3}{12}\). Then solve the problem.
Answer:
Ben has \(\frac{7}{12}\) of a book left to read. Now after some she has to read \(\frac{3}{12}\) more of the book. How much does Ben read earlier?
Explanation:
Ben has \(\frac{7}{12}\) of a book left to read.
Now after some she has to read \(\frac{3}{12}\) more of the book.
Total book Ben read earlier = \(\frac{7}{12}\) – \(\frac{3}{12}\) = \(\frac{4}{12}\)
Question 5.
Financial Literacy Financial planners suggest that \(\frac{8}{10}\) of your income should be used for spending. The rest should go into savings. If you spend \(\frac{5}{10}\) of your income to pay bills, how much of your income could you spend on other purchases?
Answer:
\(\frac{3}{10}\)
Explanation:
Financial planners suggest that \(\frac{8}{10}\) of your income should be used for spending.
If you spend \(\frac{5}{10}\) of your income to pay bills,
Total income you spend on other purchases = \(\frac{8}{10}\) – \(\frac{5}{10}\)
= \(\frac{3}{10}\)
Question 6.
Use the visual fraction model to find the difference.

Answer:
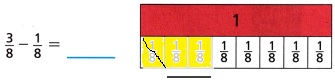
Explanation:
Subtraction operation is used to find the difference.
I’m in a Learning Mindset!
How can I share strategies and accept them from others?
Answer:
Answer may vary.
By presenting with number of model examples to understand better.