We included HMH Into Math Grade 4 Answer Key PDF Module 14 Understand Addition and Subtraction of Fractions with Like Denominators to make students experts in learning maths.
HMH Into Math Grade 4 Module 14 Answer Key Understand Addition and Subtraction of Fractions with Like Denominators

Game Designer
Game designers may design board games, puzzles, or video games. A video game designer works as part of a team and comes up with the game concept, the characters, setting, story, and game play. Designers work with artists to develop the art and animation. They also work with programmers who write the code—the directions to the computer. The designer may also be responsible for testing early versions of the game.
Other games are played with a standard deck of 52 cards. When you shuffle the cards, you change the order of the cards. Did you know that there are more possible orders of cards in a deck than stars in the Milky Way, which has between 100 and 400 billion stars?
STEM Task:
Game designers use coding to make computer games. Coding is a list of directions to the computer. You can do a simple coding activity. Use half-inch grid paper to draw a game board with multiple paths. Mark START and END. Write directions for getting from the START to the END. For example: “Make a right turn at the first intersection, then go straight, and then take the next left.” Have a classmate use a counter and follow your directions. Modify your directions, if necessary.
Learning Mindset
Perseverance Getting Unstuck

Everyone gets stuck sometimes. You try to solve a maze the way you think it should be done, but it doesn’t work. So what do you do? Do you try the same way again? Do you know if you haven’t followed the directions accurately or if the directions haven’t been written clearly? Since getting stuck happens to everyone, it’s important to develop ways to get yourself unstuck. Here are a few strategies to help you get unstuck in the STEM Task.
When writing the directions, move your counter along as you write each step.
When following directions, work your way backward to see where you made a mistake. You may even decide to start over.
Reflect
Question 1.
Describe a time you got stuck drawing your map or writing the directions to get from START to END.
Answer:
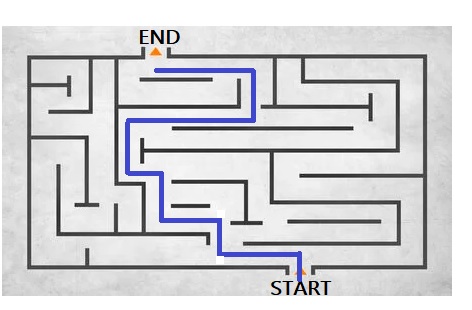
Explanation:
Make a right turn at the first intersection from starting, then go straight, and then take the next left.
After few moves than take left and keep going on and take left turn and move till you reach the end.
Question 2.
What strategies did you use to make sure the directions were clear?
Answer:
Yes, directions are clear.
Explanation:
There is a START point and END point, just we have to follow the directions to reach the goal.
Which squares show equal parts?
- Your teacher gives you four square pieces of paper and asks you to cut each piece of paper into 4 equal-sized pieces.
- You try these four patterns for your cuts.
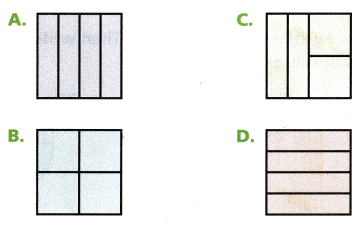
- Which squares show equal-sized pieces?
- What fraction does one of these equal-sized pieces represent?
Answer:
A, B and D are in equal size
\(\frac{1}{4}\) fraction represent the equal-sized pieces.
Explanation:
Above 4 square pieces are in equal size, each whole is divided into 4 equal parts.
\(\frac{1}{4}\) fraction represent the equal-sized pieces.
Turn and Talk
How can you prove that the four pieces in C have the same area?
Answer:
By calculating the unit area of a square.
Explanation:
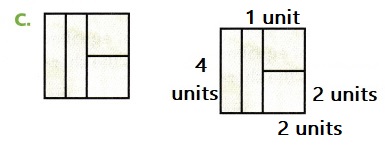
total area is 4 x 4 = 16 units
4 + 4 + 4 + 4 = 16 units
Do the fourths have to be the same shape? Explain.
Answer:
No, the fourths are not same.
Explanation:
Pieces A and D are of same size and shape and area in units
Piece B and C have different shapes of 2 different areas.
Are You Ready?
Complete these problems to review prior concepts and skills you will need for this module.
Equal Shares
Write the number of equal shares. Then write halves, thirds, or fourths to name the shares.
Question 1.

_________ equal shares
Answer:
3 equal shares
Explanation:
Whole is divided into 3 equal parts, there are 3 thirds.
So, fraction of whole is \(\frac{3}{3}\) = 1
Question 2.
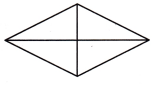
_________ equal shares
Answer:
4 equal shares
Explanation:
Whole is divided into 4 equal parts, there are 4 fourths.
So, fraction of whole is \(\frac{4}{4}\) = 1
Fractions of a Whole
Write the number of equal parts in the whole. Then write the fraction that names the shaded part.
Question 3.

equal parts: __________
fraction shaded: __________
Answer:
equal parts: 6
fraction shaded: 4
Explanation:
Whole is divided into 6 equal parts,
out of which 4 parts are shaded.
So, fraction of whole is \(\frac{4}{6}\)
Question 4.
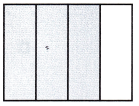
equal parts: __________
fraction shaded: __________
Answer:
equal parts: 4
fraction shaded: 3
Explanation:
Whole is divided into 4 equal parts,
out of which 3 parts are shaded.
So, fraction of whole is \(\frac{3}{4}\)
Question 5.
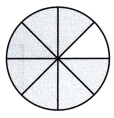
equal parts: __________
fraction shaded: __________
Answer:
equal parts: 8
fraction shaded: 7
Explanation:
Whole is divided into 8 equal parts,
out of which 7 parts are shaded.
So, fraction of whole is \(\frac{7}{8}\)
Equivalent Fractions
Shade to show the fraction. Draw a line to make an equivalent fraction. Then write the equivalent fraction.
Question 6.
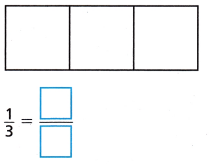
Answer:
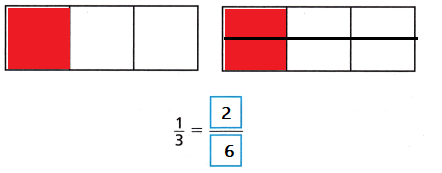
Explanation:
An equivalent fraction is a fraction that is the same as another fraction with a different denominator and numerator, by multiply with the same number to make equivalent fraction.
\(\frac{1}{3}\) = \(\frac{2}{6}\)
Question 7.
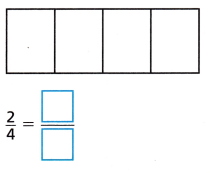
Answer:
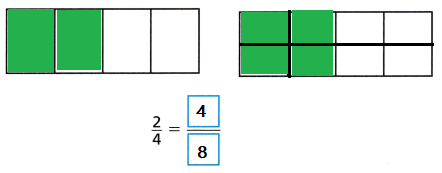
Explanation:
An equivalent fraction is a fraction that is the same as another fraction with a different denominator and numerator, by multiply with the same number to equivalent fraction.
\(\frac{2}{4}\) = \(\frac{4}{8}\)