We included HMH Into Math Grade 4 Answer Key PDF Module 13 Lesson 2 Explore Angles to make students experts in learning maths.
HMH Into Math Grade 4 Module 13 Lesson 2 Answer Key Explore Angles
I Can compare angles and use unit angles to find how many of the unit angles complete a circle.
Spark Your Learning
The Jayhawks design a flag with no angles that are the same size. The Ospreys design a flag in which two angles are the same size. Draw and describe the flag for the Ospreys.

Answer:
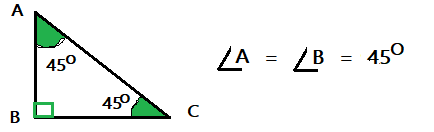
Explanation:
The Ospreys design a flag in which two angles are the same size.
The sum of total angle in the triangle is 180 degrees,
if Ospreys flag has one angle 90 degrees and rest two angles must be of 45 degrees,
as shown in the above picture.
Turn and Talk How do you know that two angles in your figure are the same size?
Answer:
According to the internal angle property the sum of triangle is 180 degrees.
Explanation:
The sum of total angle in the triangle is 180 degrees.
For example if Ospreys flag has one angle 90 degrees and rest two angle must be of 45 degrees,
as shown in the above picture.
Build Understanding
Question 1.
Competitors in an obstacle race must overcome three ramps. An angle is formed when two rays are connected at a common endpoint or vertex. The black outlines show the angles that make up each ramp.
Connect to Vocabulary
A vertex is the point where two rays of an angle meet.

A. How can you compare the angles?
Answer:
Vertex of one angle should be compared with the vertex of other angle.
Side of one angle should be compared with the other angle.
Explanation:
If the distance between the two rays is more than the angle is more than vertex.
if the distance is less than the angle is less than vertex.
B. How can you order the angles from greatest to least?
Answer:
The side opposite to the greatest angle will be the largest,
and the side opposite to the smallest angle will be the smallest.
Explanation:
An angle is formed when two rays are connected at a common endpoint or vertex.
By comparing the opposite sides of an angle, the order of angles from greatest to least be written.
Question 2.
The posts for the swing obstacle make an angle, outlined in blue. How can you make a unit angle to measure the opening of the blue angle?

A. How do you know the measure of the blue angle?
Answer:
60 degrees

Explanation:
Sum of the triangle is 180 degrees
Each side of a triangle is 60 degrees
So, the angle between both the blue lines are,
30 + 30 = 60 degrees angle between the blue lines.
B. What is the measure of the blue angle?
Answer:
60 degrees
Explanation:
30 + 30 =60 degrees angle between the blue lines
Question 3.
A wagon wheel is in the shape of a circle. It has wooden spokes that connect directly from the hub to the rim forming an angle. How many of these unit angles come together in the center of the circle?

A. How can you use the unit angle to find the number of angles that make up the circle?
Answer:
Angle subtended by a portion of the circumference equal in length to the radius of the circle is unit angle.

Explanation:
Angle of a circle is 180 degrees.
So, the circle is divided into total 8 parts.
\(\frac{360}{8}\) = 45 degrees each angle
B. _______ angles come together in the center of the circle.
Answer:
8 angles
Explanation:
Complete angles in a circle is 360 degrees.
The angles come together in the center of the circle of each is 45 degrees.
Turn and Talk If you shade 3 of the angles you traced in the circle, what part of the circle is shaded? How do you know?
Answer:
\(\frac{3}{8}\) part is shaded as 135 degrees.
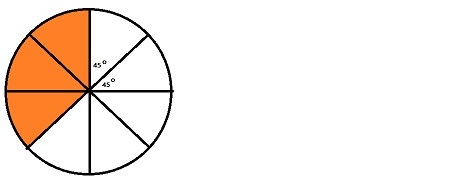
Explanation:
Circle is divided into 8 equal parts, out of which 3 parts are shaded.
\(\frac{3}{8}\) part is shaded
360 x \(\frac{3}{8}\) = 45 x 3 = 135 degrees
Check Understanding
Question 1.
Kenya draws angles to make a design for a team’s jerseys. Circle the angles that appear to be the same size.
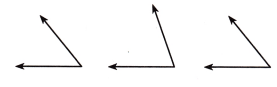
Answer:
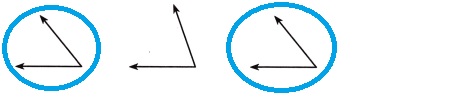
Explanation:
Two corner angles are of same size, in the first and third angles.
Question 2.
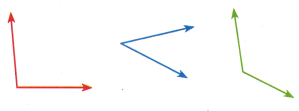
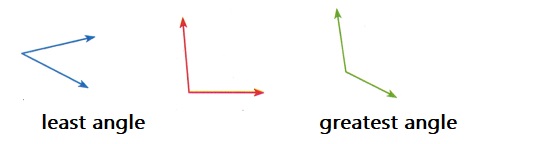
Compare the angles. Then use the angle colors to write the angles in order from least to greatest.
Answer:
Green color angle is greatest angle and blue color angle is least angle as shown below picture.
Explanation:
As the two lines in the blue angle are near to each other thus the angle is the least,
and the two lines in the green angle are far to each other thus the angle is the greatest.
Question 3.
Using the unit angle shown, how many unit angles come together in the center of the circle?
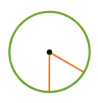
Answer:
6 unit angles of each 60 degrees
Explanation:
The ratio of the length of the arc of a circle to the radius of that circle is known ass unit angle.
360 x \(\frac{1}{6}\) = 60 degrees
On Your Own
Question 4.
Reason Austin makes a poster to display the rules of an obstacle course race. The poster will be in a shape that has 2 pairs of angles that are the same size. Draw what the poster might look like.
How do you know the angle pairs are the same size?
Answer:

Explanation :
The above poster has 2 green angles and two red angles thus forming 2 pairs of angles.
Question 5.
Compare the angles. Then use the angle colors to write the angles in order from greatest to least.
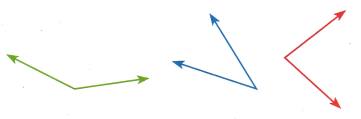
Answer:
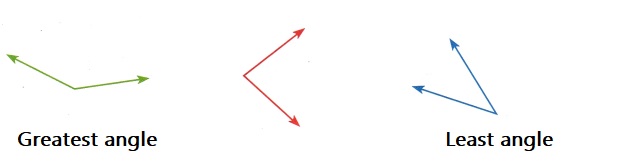
Explanation:
As the two lines in the blue angle are near to each other thus the angle is the least,
and the two lines in the green angle are far to each other thus the angle is the greatest.
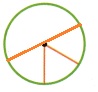
Question 6.
Using the unit angle shown, how many unit angles come together in the center of the circle?
Answer:
12 unit angles.
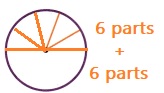
Explanation:
12 unit angles come together in the center of the circle
as shown above with each 30 degrees of angle.
\(\frac{360}{122}\) = 30 degrees
Question 7.
Open Ended Make a unit angle to measure the green angle. What is the measure of the green angle?
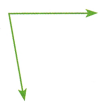
Answer:
72 Degrees
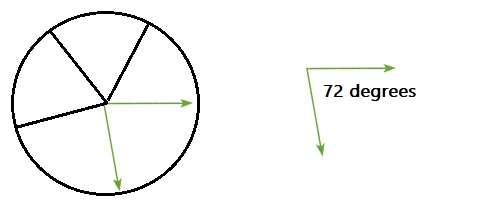
Explanation:
5 unit angles come together in the circle,
as shown above with each 72 degrees of angle.
\(\frac{360}{5}\) = 72 degrees
I’m in a Learning Mindset!
How did I work with a partner when solving the Turn and Talk?
Answer:
Turn and Talk is a strategy that benefits both types of learners.
Explanation:
In Turn and Talk interaction takes place between both the partners.
One of the partner is always passive and the other one is active and defend their choice.