We included HMH Into Math Grade 4 Answer Key PDF Module 11 Lesson 7 Use Comparisons to Order Fractions to make students experts in learning maths.
HMH Into Math Grade 4 Module 11 Lesson 7 Answer Key Use Comparisons to Order Fractions
Use Comparisons to Order Fractions
I Can use different strategies to compare and order three or more fractions.

Step It Out
1. Elizabeth’s soccer team is designing a new team flag. Their team colors are green and yellow. They are considering three same sized designs. Which design has the least green fabric? Which has the most?
Answer:
Design 2 has the least green fabric and Design 3 has the most green fabric.
Explanation:
Length of green fabric(Design 1) = \(\frac{3}{5}\)
Length of green fabric(Design 2) = \(\frac{1}{8}\)
Length of green fabric(Design 3) = \(\frac{9}{10}\)
Order from least:
\(\frac{1}{8}\)
\(\frac{3}{5}\)
\(\frac{9}{10}\)
Compare the fractions and order them from least to greatest.
A. Compare each fraction to the benchmark \(\frac{1}{2}\)
\(\frac{3}{5}\) ![]() \(\frac{1}{2}\) \(\frac{1}{8}\)
\(\frac{1}{2}\) \(\frac{1}{8}\) ![]() \(\frac{1}{2}\) \(\frac{9}{10}\)
\(\frac{1}{2}\) \(\frac{9}{10}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
____ and ____ are both greater than \(\frac{1}{2}\).
So, ___ is the least fraction.
B. Write equivalent fractions to compare the two fractions that are greater than \(\frac{1}{2}\)
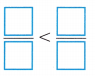
C. Write the original fractions in order, from least to greatest.
_______________________________
D. Identify the flag design that has the least green fabric and the flag design that has the most green fabric.
_______________________________
Answer:
\(\frac{1}{8}\) flag design that has the least green fabric and \(\frac{9}{10}\) flag design that has the most green fabric.
Explanation:
\(\frac{3}{5}\) > \(\frac{1}{2}\)
\(\frac{1}{8}\) < \(\frac{1}{2}\)
\(\frac{9}{10}\) > \(\frac{1}{2}\)
\(\frac{3}{5}\) and \(\frac{9}{10}\) are both greater than \(\frac{1}{2}\).
So, \(\frac{1}{8}\) is the least fraction.
Equivalent fractions:
\(\frac{3}{5}\) = \(\frac{3}{5}\) × \(\frac{2}{2}\) = \(\frac{6}{10}\)
\(\frac{9}{10}\) = \(\frac{9}{10}\) × \(\frac{2}{2}\) = \(\frac{18}{20}\)
Order from least:
\(\frac{1}{8}\)
\(\frac{3}{5}\)
\(\frac{9}{10}\)
Turn and Talk How could you have used a different strategy to compare and order the fractions?
Answer:
Denominators tell us the size of the pieces.
Numerators tell us the number of pieces.
We can only directly compare fractions with the same size whole.
Explanation:
Order from least:
\(\frac{1}{8}\) => Ratio is 1:8 => out of 8 parts 1 part is green.
\(\frac{3}{5}\) => Ratio is 3:5 => out of 5 parts 5 part is green.
\(\frac{9}{10}\) => Ratio is 9:10 => out of 10 parts 9 part is green.
Step It Out
2. At the end of the soccer team party, parts of three medium pizzas are left. There is 4 of a cheese pizza, of a pepperoni pizza, and \(\frac{1}{2}\) of a veggie pizza. Elizabeth wants to compare the amounts of pizza left.
Use a common denominator to compare the fractions.
A. List multiples of the three denominators.

Multiples of 2: ________
Multiples of 4: ________
Multiples of 6: ________
B. Use a common multiple to write equivalent fractions.

C. Use the equivalent fractions to write the original fractions in order, from least to greatest. _____________
D. Write the pizzas in order, from least amount left to greatest amount left. _____________
Answer:
Order from least amount left to greatest amount left:
\(\frac{6}{12}\)
\(\frac{9}{12}\)
\(\frac{10}{12}\)
Explanation:
Number of cheese pizza = \(\frac{5}{6}\).
Number of pepperoni pizza = \(\frac{3}{4}\).
Number of veggie pizza = \(\frac{1}{2}\)
Multiples of 2: 2,4,6,8,10,12,14,16,18,20.
Multiples of 4: 4,8,12,16,20,24,28,32,36,40.
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Common multiple of 2,4, 6 = 12.
\(\frac{5}{6}\) = \(\frac{5}{6}\) × \(\frac{2}{2}\) = \(\frac{10}{12}\)
\(\frac{3}{4}\) = \(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\)
\(\frac{1}{2}\) = \(\frac{1}{2}\) × \(\frac{6}{6}\) = \(\frac{6}{12}\)
Order from least amount left to greatest amount left:
\(\frac{6}{12}\)
\(\frac{9}{12}\)
\(\frac{10}{12}\)
Check Understanding Math Board
Question 1.
Roger, Haley, and Ji-ho make the same-sized burritos. Roger eats \(\frac{4}{6}\) of his burrito. Haley eats \(\frac{6}{8}\) of hers, and Ji-ho eats \(\frac{4}{10}\) of his. Who eats the least and greatest amounts of burrito? Explain.
Answer:
Least and greatest amounts of burrito:
\(\frac{48}{120}\)
\(\frac{80}{120}\)
\(\frac{90}{120}\)
Explanation:
Amount of burritos Roger eats = \(\frac{4}{6}\)
Amount of burritos Haley eats = \(\frac{6}{8}\)
Amount of burritos Ji-ho eats = \(\frac{4}{10}\)
Multiples of 6: 6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96,102,108,114,120.
Multiples of 8: 8,16,24,32,40,56,64,72,80,88,96,104,112,120.
Multiples of 10: 10,20,30,40,50,60,70,80,90,100,110,120.
Common multiple of 6,8 n 10 = 120.
\(\frac{4}{6}\) = \(\frac{4}{6}\) × \(\frac{20}{20}\) = \(\frac{80}{120}\)
\(\frac{6}{8}\) = \(\frac{6}{8}\) × \(\frac{15}{15}\) = \(\frac{90}{120}\)
\(\frac{4}{10}\) = \(\frac{4}{10}\) × \(\frac{12}{12}\) = \(\frac{48}{120}\)
Least and greatest amounts of burrito:
\(\frac{48}{120}\)
\(\frac{80}{120}\)
\(\frac{90}{120}\)
On Your Own
Question 2.
Aaron’s soccer team is voting on a new team flag. They are voting on three designs. Each flag is the same size. Design 1 is \(\frac{2}{3}\) blue. Design 2 is \(\frac{1}{6}\) blue. Design 3 is \(\frac{3}{8}\) blue.

Compare the amount of blue in each design.
Write the flag designs in order, from least amount of blue to greatest amount of blue.
_______________________________
Answer:
Flag designs in order, from least amount of blue to greatest amount of blue:
\(\frac{4}{24}\)
\(\frac{9}{24}\)
\(\frac{16}{24}\)
Explanation:
Design 1 = \(\frac{2}{3}\) blue.
Design 2 = \(\frac{1}{6}\) blue.
Design 3 = \(\frac{3}{8}\) blue.
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Multiples of 8: 8,16,24,32,40,56,64,72,80.
Multiples of 3: 3,6,9,12,15,18,21,24,27,30.
Common multiple of 6,8 n 3 = 24.
\(\frac{2}{3}\) = \(\frac{2}{3}\) × \(\frac{8}{8}\) = \(\frac{16}{24}\)
\(\frac{1}{6}\) = \(\frac{1}{6}\) × \(\frac{4}{4}\) = \(\frac{4}{24}\)
\(\frac{3}{8}\) = \(\frac{3}{8}\) × \(\frac{3}{3}\) = \(\frac{9}{24}\)
Flag designs in order, from least amount of blue to greatest amount of blue:
\(\frac{4}{24}\)
\(\frac{9}{24}\)
\(\frac{16}{24}\)
Question 3.
Compare each fraction to the benchmark \(\frac{1}{2}\). Then write the three fractions in order from least to greatest.
\(\frac{7}{8}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
\(\frac{3}{6}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
\(\frac{4}{10}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
Answer:
\(\frac{7}{8}\) > \(\frac{1}{2}\)
\(\frac{3}{6}\) = \(\frac{1}{2}\)
\(\frac{4}{10}\) < \(\frac{1}{2}\)
Explanation:
\(\frac{7}{8}\) > \(\frac{1}{2}\)
\(\frac{3}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{1}{2}\)
\(\frac{4}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{5}\)
Question 4.
Write the fractions in order, from least to greatest: \(\frac{3}{4}\), \(\frac{5}{6}\), \(\frac{9}{10}\).
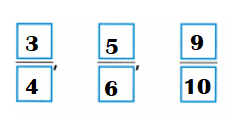
Answer:
Explanation:
\(\frac{3}{4}\) = 0.75
\(\frac{5}{6}\) = 0.875
\(\frac{9}{10}\) = 0.9
The fractions in order, from least to greatest:
\(\frac{3}{4}\)
\(\frac{5}{6}\)
\(\frac{9}{10}\)
Question 5.
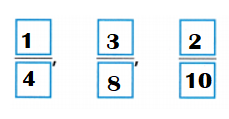
Write the fractions in order, from least to greatest: \(\frac{1}{4}\), \(\frac{3}{8}\), \(\frac{2}{10}\).
Answer:
Explanation:
\(\frac{1}{4}\) = 0.25.
\(\frac{3}{8}\) = 0.375
\(\frac{2}{10}\) = 0.2
the fractions in order, from least to greatest:
\(\frac{2}{10}\)
\(\frac{1}{4}\)
\(\frac{3}{8}\)
Reason Write a numerator that makes the statement true.
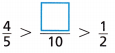
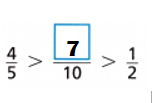
Question 6.
Answer:
Explanation:
\(\frac{4}{5}\) = 0.8
Add numerators: (4 × 2) – 1 = 7. {Denominator = 5 × 2 = 10)
\(\frac{??}{10}\) = \(\frac{7}{10}\) = 0.7
\(\frac{1}{2}\) = 0.5
Question 7.
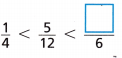
Answer:
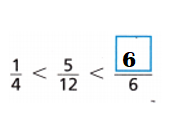
Explanation:
\(\frac{1}{4}\) = 0.25
\(\frac{5}{12}\) = 0.42
Add numerators : ?? = 1 + 5 = 6.
\(\frac{??}{6}\) = \(\frac{}{6}\) = 1
Question 8.
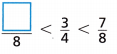
Answer:
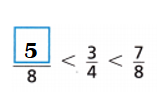
Explanation:
\(\frac{3}{4}\)
Add Numerators: 3 + 2 = 5. [Denominator 4 × 2 = 8]
\(\frac{??}{8}\) = \(\frac{5}{8}\) = 0.625.
\(\frac{3}{4}\) = 0.75
\(\frac{7}{8}\) = 0.875
On Your Own
Question 9.
Reason Carrie, Jill, and Skylar record the distances they each swam at practice. The table shows the distances they swam. Show the order that Carrie, Jill, and Skylar swam, from least to greatest distance. Use fraction comparison strategies to justify your comparisons.

Answer:
The order, from least to greatest distance:
Distance Skylar swam = \(\frac{12}{10}\) kilometers = 1.2 kilometers.
Distance Carrie swam = \(\frac{12}{8}\) kilometers = 1.5 kilometers.
Distance Jill swam = \(\frac{10}{6}\) kilometers = 1.67 kilometers.
Explanation:
Distance Carrie swam = \(\frac{12}{8}\) kilometers = 1.5 kilometers.
Distance Jill swam = \(\frac{10}{6}\) kilometers = 1.67 kilometers.
Distance Skylar swam = \(\frac{12}{10}\) kilometers = 1.2 kilometers.
Question 10.
Compare each fraction to the benchmark. Then write the fractions in order from least to greatest.
\(\frac{8}{8}\) ![]() 1 \(\frac{12}{11}\)
1 \(\frac{12}{11}\) ![]() 1 \(\frac{10}{12}\)
1 \(\frac{10}{12}\) ![]() 1
1
Answer:
The fractions in order from least to greatest:
\(\frac{10}{12}\)
\(\frac{8}{8}\)
\(\frac{12}{11}\)
Explanation:
\(\frac{8}{8}\) = 1
\(\frac{12}{11}\) = 1.09 >1.
\(\frac{10}{12}\) = 0.83 <1
Question 11.
Write the fractions in order, from least to greatest: \(\frac{1}{4}\), \(\frac{3}{6}\), \(\frac{1}{8}\).

Answer:
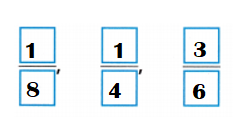
Explanation:
\(\frac{1}{4}\) = 0.25
\(\frac{3}{6}\) = \(\frac{3}{6}\) ÷ \(\frac{3}{3}\) = \(\frac{1}{2}\) = 0.5.
\(\frac{1}{8}\) = 0.125
The fractions in order, from least to greatest:
\(\frac{1}{8}\)
\(\frac{1}{4}\)
\(\frac{3}{6}\)
Question 12.
Write the fractions in order, from greatest to least: \(\frac{14}{10}\), \(\frac{8}{5}\), \(\frac{7}{8}\).

Answer:
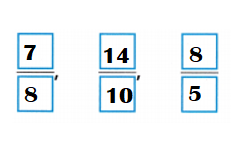
Explanation:
\(\frac{14}{10}\) = \(\frac{14}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{7}{5}\) = 1.4
\(\frac{8}{5}\) = 1.6
\(\frac{7}{8}\) = 0.875.
The fractions in order, from greatest to least:
\(\frac{7}{8}\)
\(\frac{14}{10}\)
\(\frac{8}{5}\)
Question 13.
Critique Reasoning Sasha says that the fractions \(\frac{2}{3}\), \(\frac{3}{6}\), \(\frac{4}{10}\) are in order from least to greatest because the numerators are in order from least to greatest. Is Sasha correct? Explain.
Answer:
Sasha is not correct because denominators having less numbers means their value is bigger than others.
Fractions order from least to greatest:
\(\frac{4}{10}\)
\(\frac{3}{6}\)
\(\frac{2}{3}\)
Explanation:
\(\frac{2}{3}\) = 0.67
\(\frac{3}{6}\) = \(\frac{3}{6}\) ÷ \(\frac{3}{3}\) = \(\frac{1}{2}\) = 0.5
\(\frac{4}{10}\) = \(\frac{4}{10}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{5}\) = 0.4