Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison

/ By

We included HMH Into Math Grade 4 Answer Key PDF Module 11 Fraction Equivalence and Comparison to make students experts in learning maths.

HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison

Which Square Does Not Belong

Look at the squares below. Write a fraction that represents the shaded portion of each square.
A.
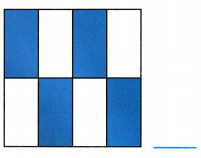
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 1
Answer:
Fraction of the shaded portions of square = \(\frac{4}{8}\)

Explanation:
Total number of portions in the square = 8
Number of shaded portions in the square = 4
Fraction of the shaded portion of square = Number of shaded portions in the square ÷ Total number of portions in the square
= \(\frac{4}{8}\)

B.
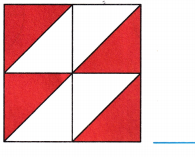
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 2

Answer:
Fraction of the shaded portion of square = \(\frac{4}{8}\)

Explanation:
Total number of portions in the square = 8
Number of shaded portions in the square = 4
Fraction of the shaded portion of square = Number of shaded portions in the square ÷ Total number of portions in the square
= \(\frac{4}{8}\)

C.
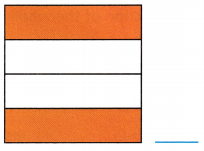
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 3

Answer:
Fraction of the shaded portion of square = \(\frac{2}{4}\)

Explanation:
Total number of portions in the square = 4
Number of shaded portions in the square = 2
Fraction of the shaded portion of square = Number of shaded portions in the square ÷ Total number of portions in the square
= \(\frac{2}{4}\)

D.
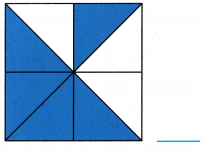
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 4

Answer:
Fraction of the shaded portion of square = \(\frac{5}{8}\)

Explanation:
Total number of portions in the square = 8
Number of shaded portions in the square = 5
Fraction of the shaded portion of square = Number of shaded portions in the square ÷ Total number of portions in the square
= \(\frac{5}{8}\)

 

Turn and Talk

  • Which square’s shading represents a different amount?
    Answer:
    C. Fraction of the shaded portion of square = \(\frac{2}{4}\) square’s shading represents a different amount.Explanation:
    A. Fraction of the shaded portions of square = \(\frac{4}{8}\)
    B. Fraction of the shaded portion of square = \(\frac{4}{8}\)
    C. Fraction of the shaded portion of square = \(\frac{2}{4}\)
    D. Fraction of the shaded portion of square = \(\frac{5}{8}\)
  • How could you change the shading in that square to make it represent the same amount as the others?
    Answer:
    You change the shading in that square to make it represent the same amount as the others by changing its numerator.Explanation:
    Denominator tells us how many equal parts to divide the shape into.
    Numerator tells us how many parts are shaded in the shape.

Are You Ready?
Complete these problems to review prior concepts and skills you wIll vised for this module.

Part of a Whole
Find the fraction of the whole that is shaded.
1. There are ______ equal parts.
There are _____ shaded parts.
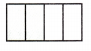
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 5
___ out of __equalpartsareshaded.
The fraction of the whole that is shaded is ___.
Answer:
Fraction of the whole that is shaded = \(\frac{0}{4}\) = 0.

Explanation:
Total number of portions in the figure = 4.
Number of shaded portions in the figure = 0.
Fraction of the whole that is shaded = Number of shaded portions in the figure ÷ Total number of portions in the figure
= \(\frac{0}{4}\)
= 0.

Name the Shaded Part
Write a fraction to name the shaded part of the whole.
Question 2.
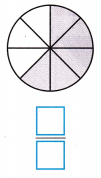
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 6
Answer:
Fraction of the whole that is shaded = \(\frac{5}{8}\)
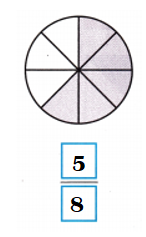
HMH-Into-Math-Grade-4-Module-11-Answer-Key-Fraction-Equivalence-and-Comparison-Name the Shaded Part-2

Explanation:
Total number of portions in the figure = 8.
Number of shaded portions in the figure = 5.
Fraction of the whole that is shaded = Number of shaded portions in the figure ÷ Total number of portions in the figure
= \(\frac{5}{8}\)

 

Question 3.
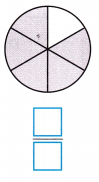
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 7
Answer:
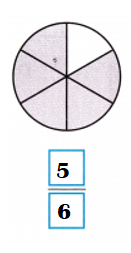
HMH-Into-Math-Grade-4-Module-11-Answer-Key-Fraction-Equivalence-and-Comparison-Name the Shaded Part-3

Explanation:
Total number of portions in the figure = 6.
Number of shaded portions in the figure = 5.
Fraction of the whole that is shaded = Number of shaded portions in the figure ÷ Total number of portions in the figure
= \(\frac{5}{6}\)

 

Question 4.
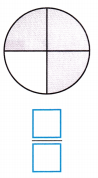
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 8
Answer:
Fraction of the whole that is shaded = \(\frac{3}{4}\)
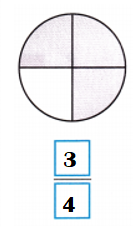
HMH-Into-Math-Grade-4-Module-11-Answer-Key-Fraction-Equivalence-and-Comparison-Name the Shaded Part-4

Explanation:
Total number of portions in the figure = 4.
Number of shaded portions in the figure = 3.
Fraction of the whole that is shaded = Number of shaded portions in the figure ÷ Total number of portions in the figure
= \(\frac{3}{4}\)

 

Compare Parts of a Whole
Shade the fraction strips to show the fractions. Then circle the greater fraction.
Question 5.
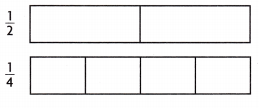
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 9
Answer:
\(\frac{1}{2}\) > \(\frac{1}{4}\)
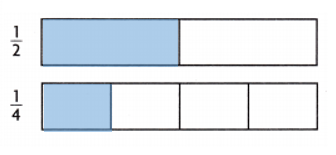
HMH-Into-Math-Grade-4-Module-11-Answer-Key-Fraction-Equivalence-and-Comparison-Compare Parts of a Whole-5

Explanation:
\(\frac{1}{2}\) = 0.5.
\(\frac{1}{4}\) = 0.25.

Question 6.
HMH Into Math Grade 4 Module 11 Answer Key Fraction Equivalence and Comparison 10
Answer:
\(\frac{1}{6}\) < \(\frac{1}{3}\)
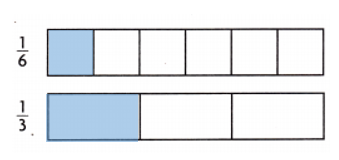
HMH-Into-Math-Grade-4-Module-11-Answer-Key-Fraction-Equivalence-and-Comparison-Compare Parts of a Whole-6

Explanation:
\(\frac{1}{6}\) = 0.17.
\(\frac{1}{3}\) = 0.33

Leave a Comment

Scroll to Top
Scroll to Top