We included HMH Into Math Grade 3 Answer Key PDF Module 4 Lesson 3 Understand the Associative Property of Multiplication to make students experts in learning maths.
HMH Into Math Grade 3 Module 4 Lesson 3 Answer Key Understand the Associative Property of Multiplication
I Can multiply three factors by using the Associative and Commutative Properties of Multiplication.
Spark Your Learning
Each week, Cory works in the vegetable garden for 2 hours on each of 3 days. He works for 2 weeks. How many hours does Cory work in 2 weeks?

Show more than one way to find the number of hours.

Answer:
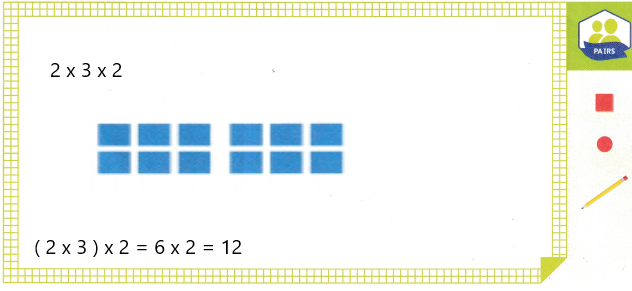
Explanation:
Each week, Cory works in the vegetable garden for 2 hours on each of 3 days
He works for 2 weeks
To find how many hours Cory work in 2 weeks
Multiply
2 x 3 x 2
= (2 x 3 ) x 2
= 6 x 2
= 12
So, 2 x 3 x 2 = 12
Therefore, Cory works for 12 hours in 2 weeks.
Turn and Talk Does it matter whether you multiply the number of hours by the number of days worked first or multiply the number of days worked by the number of weeks first? Explain your answer.
Answer:
The Associative Property of Multiplication states that when the grouping of factors is changed, the product remains the same.
So, it doesn’t matter whether we multiply the number of hours by the number of days worked first or multiply the number of days worked by the number of weeks first because the answer will be same.
Build Understanding
1. Each week, Lila rakes leaves for 3 hours on each of 2 days. She has raked leaves for 4 weeks. How many hours has Lila raked leaves in 4 weeks?

A. How can you use an array to help solve the problem? Complete the array.
4 × (2 × 3) = ![]()

Answer:
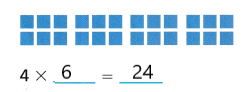
Explanation:
Each week, Lila rakes leaves for 3 hours on each of 2 days
She has raked leaves for 4 weeks
I completed the array by drawing one more group of a 2 x 3 array
4 × (2 × 3)
= 4 x 6
= 24
So, Lila raked leaves for 24 hours.
Connect to Vocabulary
The Associative Property of Multiplication states that when the grouping of factors is changed, the product remains the same.
Example:
(5 × 2) × 4 = 40
5 × (2 × 4) = 40
B. How can you change the grouping of the factors, using parentheses? Complete the array.
4 × 2 × 3 = ![]()
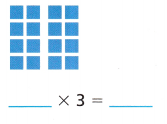
Answer:
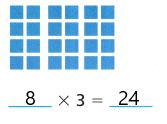
Explanation:
Each week, Lila rakes leaves for 3 hours on each of 2 days
She has raked leaves for 4 weeks
I completed the array by drawing one more group of a 4 x 2 array
( 4 × 2 ) × 3
= 8 x 3
= 24
So, Lila raked leaves for 24 hours.
C. For how many hours has Lila raked leaves?
Answer:
Lila raked leaves for 24 hours.
Turn and Talk Explain why the operation inside the parentheses should be completed first.
Answer:
The operation in the brackets should be completed first so that it will be easy to multiply the answer of the parentheses to other number in the three numbers.
2. For 5 days each week, Paola helps paint rooms for 4 hours each day. She helps paint rooms for 2 weeks. For how many hours does Paola help paint in 2 weeks?

You can change the grouping or the order of factors. The product is the same. Complete the equations to show changing the grouping and the order of factors.
(5 × 4) × 2 = ![]()
5 × (4 × 2) = ![]() ← Associative Property
← Associative Property
5 × ____ = ___ hours
5 × (4 × 2) = ![]()
5 × (2 × 4) = ![]() ← Commutative Property
← Commutative Property
(5 × 2) × 4 = ![]() ← Associative Property
← Associative Property
___ × ___ = ___ hours
Answer:
40 hours
Explanation:
For 5 days each week, Paola helps paint rooms for 4 hours each day
She helps paint rooms for 2 weeks
(5 × 4) × 2 = 20 x 2 = 40
5 × (4 × 2) = 5 x 8 = 40 ← Associative Property
5 × 8 = 40 hours
5 × (4 × 2) = 5 x 8 = 40
5 × (2 × 4) = 5 x 8 = 40 ← Commutative Property
(5 × 2) × 4 = 10 x 4 = 40 ← Associative Property
10 x 4 = 40 hours
Paola helps paint in 2 weeks for 40 hours.
Turn and Talk Explain how the Commutative and Associative Properties of Multiplication are alike and how they are different.
Answer:
The associative property states that you can re-group numbers and you will get the same answer and the commutative property states that you can move numbers around and still arrive at the same answer. The difference is in associative property we re-group numbers and in commutative property we move the numbers.
Check Understanding Math Board
Question 1.
For 4 days each week, Jed helps build a fence for 3 hours each day. He works on the fence for 2 weeks. For how many hours does Jed work in 2 weeks?
Answer:
24 hours
Explanation:
For 4 days each week, Jed helps build a fence for 3 hours each day
He works on the fence for 2 weeks
4 x 3 x 2
= 4 x ( 3 x 2 )
= 4 x 6
= 24
So, Jed works for 24 hours in 2 weeks.
On Your Own
Question 2.
Model with Mathematics On each day of her pottery class, Jayla makes 6 bowls in the morning and 6 bowls in the afternoon. She has made bowls for 3 days.
Draw an array to make a visual model. Write an equation for the arrays. Then show another way to group the factors and solve.
Answer:
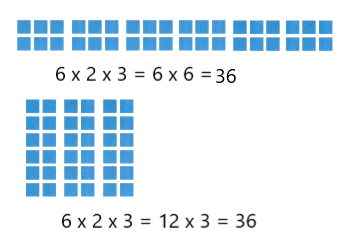
Explanation:
On each day of her pottery class, Jayla makes 6 bowls in the morning and 6 bowls in the afternoon
She has made bowls for 3 days
6 x 2 x 3
= 6 (2 x 3 )
= 6 x 6
= 36
So, the equation is 6 (2 x 3 ) = 36
Another way:
6 x 2 x 3
= (6 x 2 ) x 3
= 12 x 3
= 36
So, the equation is (6 x 2 ) x 3 = 36.
Show another way to group the factors. Then find the product.
Question 3.
2 × (5 × 6)
_____
Answer:
60
Explanation:
(2 × 5) × 6)
= 10 x 6
= 60
So, 2 × (5 × 6) = 60.
Question 4.
(8 × 2) × 3
_______
Answer:
48
Explanation:
8 × (2 × 3)
= 8 x 6
= 48
So, (8 × 2) × 3 = 48.
Reason Write the unknown number.
Question 5.
3 × (6 × 2) = 6 × (2 × ___)
Answer:
3
Explanation:
The Associative Property of Multiplication states that when the grouping of factors is changed, the product remains the same.
We know that 3 × (6 × 2) = 6 × (2 × ___)
The number that is in first equation and not in the second number is the missing number
So, the missing number in the above equation is 3.
Question 6.
(7 × 2) × 3 = 7 × (__ × 2)
Answer:
3
Explanation:
The Associative Property of Multiplication states that when the grouping of factors is changed, the product remains the same.
We know that (7 × 2) × 3 = 7 × (__ × 2)
The number that is in first equation and not in the second number is the missing number
So, the missing number in the above equation is 3.
Question 7.
STEM Computers use a system called the Binary Number System. The digits in a number can be either 0 or 1. The 0 means off and the 1 means on. To show the number 9 in the Binary Number System, look at the table. Multiply the factors in the parentheses o in each place. If the product is 0, write 0 in that place. If the product is not 0, write 1 in that place.
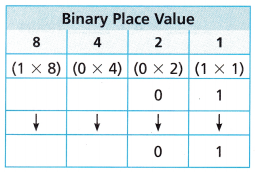
Answer:
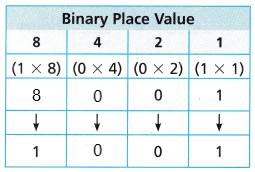
Explanation:
Multiply the factors in the parentheses o in each place
If the product is 0, write 0 in that place
If the product is not 0, write 1 in that place
So, The product of 0 and 4 is 0 so, i wrote 0
The product of 1 x 8 = 8 and 8 is not 0. So, i wrote 1.
I’m in a Learning Mindset!
What do I do when I’m learning something new? What helps me remember what to do?
_________________________________