We included HMH Into Math Grade 3 Answer Key PDF Module 20 Lesson 1 Draw Quadrilaterals to make students experts in learning maths.
HMH Into Math Grade 3 Module 20 Lesson 1 Answer Key Draw Quadrilaterals
Spark Your Learning
I Can draw a quadrilateral given descriptions of the sides and angles in the shape. I can group quadrilaterals using the side lengths or number of right angles.
An architect is asked to design an outdoor theater stage in the shape of a quadrilateral. The stage must have 2 pairs of parallel sides, no right angles, and at least 2 sides that are different in length.

Draw a design that the architect could use.

Answer:
In Geometry, a parallelogram is a type of quadrilateral. It is a two-dimensional figure with four sides. The most important properties of a parallelogram are that the opposite sides are parallel and congruent and the opposite angles are also equal.

Properties of parallelogram:
A parallelogram is a closed four-sided two-dimensional figure in which the opposite sides are parallel and equal in length. Also, the opposite angles are also equal. Learning the properties of a parallelogram is useful in finding the angles and sides of a parallelogram. The four most important properties of a parallelogram are:
– The opposite sides of a parallelogram are equal in measurement and they are parallel to each other.
– The opposite angles of a parallelogram are equal.
– The sum of interior angles of a parallelogram is equal to 360°.
– The consecutive angles of a parallelogram should be supplementary (180°).
Turn and Talk How would the architect’s design change if the stage has only 1 pair of parallel sides?
Answer: We can draw a trapezoid.
A trapezoid is a polygon that has only one pair of parallel sides. These parallel sides are also called parallel bases of trapezoid. The other two sides of trapezoids are non-parallel and called legs of trapezoids.
Properties:
There are certain properties of trapezoids that identify them as trapezoids:
– The base angles and the diagonals of an isosceles trapezoid are equal.
– If you draw a median on a trapezoid, it will be parallel to the bases and its length will be the average of the length of the bases.
– The intersection point of the diagonals is collinear to the midpoints of the two opposite sides.
– If there is a trapezoid with sides a, b, c and d and diagonals p and q, the following equation will be true: p2+q2= c2+d2+2ab.
Build Understanding
Question 1.
Draw a quadrilateral that has 2 pairs of opposite sides that are equal in length, 2 pairs of opposite parallel sides, and 4 right angles.

A. To which quadrilateral categories does the shape you drew belong?
Answer: Rectangle
– A Rectangle is a four sided-polygon, having all the internal angles equal to 90 degrees. The two sides at each corner or vertex, meet at right angles. The opposite sides of the rectangle are equal in length which makes it different from a square.
– A rectangle is a type of quadrilateral that has its parallel sides equal to each other and all four vertices are equal to 90 degrees. Hence, it is also called an equiangular quadrilateral. Since, the opposite sides are equal and parallel, in a rectangle, therefore, it can also be termed as a parallelogram.
The shape of the rectangle:
A rectangle is a two-dimensional flat shape. In an XY plane, we can easily represent a rectangle, where the arms of x-axis and y-axis show the length and width of the rectangle, respectively.
Rectangular shaped objects: The most common everyday things or objects we see and are rectangular in shape is Television, computer screen, notebook, mobile phones, CPU, Notice boards, Table, Book, TV screen, Mobile phone, Wall, Magazine, Tennis court, etc.
B. How do you know the shape you drew belongs to those categories?
Answer: In the question asked 2 pairs of opposite sides that are equal in length, 2 pairs of opposite parallel sides, and 4 right angles. These all properties belong to a rectangle. So we can easily identify and draw a rectangle. The properties of a rectangle are given below:
– It has four sides and four vertices
– Each vertex has an angle equal to 90 degrees
– The opposite sides are equal and parallel
– Diagonals bisect each other
– Perimeter is equal to twice some of its length and breadth
– The area is equal to the product of its length and breadth
– It’s a parallelogram with four right angles.
– Sum of all interior angles equal to 360 degrees
Question 2.
Look at the quadrilaterals.
A. What name do all of the quadrilaterals in this group share?
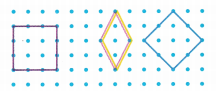
Answer: square and rhombus
Rhombus:
A rhombus is a special case of a parallelogram, and it is a four-sided quadrilateral. In a rhombus, opposite sides are parallel and the opposite angles are equal. Moreover, all the sides of a rhombus are equal in length, and the diagonals bisect each other at right angles. The rhombus is also called a diamond or rhombus diamond. The plural form of a rhombus is rhombi or rhombuses.
Properties:
– All sides of the rhombus are equal.
– The opposite sides of a rhombus are parallel.
– Opposite angles of a rhombus are equal.
– In a rhombus, diagonals bisect each other at right angles.
– Diagonals bisect the angles of a rhombus.
– The sum of two adjacent angles is equal to 180 degrees.
– The two diagonals of a rhombus form four right-angled triangles which are congruent to each other
– You will get a rectangle when you join the midpoint of the sides.
– You will get another rhombus when you join the midpoints of half the diagonal.
– Around a rhombus, there can be no circumscribing circle.
– Within a rhombus, there can be no inscribing circle.
– You will get a rectangle, where the midpoints of the 4 sides are joined together, and the length and width of the rectangle will be half the value of the main diagonal so that the area of the rectangle will be half of the rhombus.
Square: Square is a regular quadrilateral, which has all the four sides of equal length and all four angles are also equal. The angles of the square are at right-angle or equal to 90-degrees. Also, the diagonals of the square are equal and bisect each other at 90 degrees. A square can also be defined as a rectangle where two opposite sides have equal length.
Properties of square:
– All four interior angles are equal to 90°
– All four sides of the square are congruent or equal to each other
– The opposite sides of the square are parallel to each other
– The diagonals of the square bisect each other at 90°
– The two diagonals of the square are equal to each other
– The square has 4 vertices and 4 sides
– The diagonal of the square divide it into two similar isosceles triangles
– The length of diagonals is greater than the sides of the square
B. Draw a quadrilateral that does not belong to this group. Explain why this shape does not belong to the group.

Answer: I would draw a trapezoid because it is with one parallel side and two pairs of opposing angles.
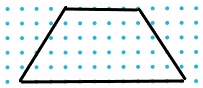
There are certain properties of trapezoids that identify them as trapezoids:
– The base angles and the diagonals of an isosceles trapezoid are equal.
– If you draw a median on a trapezoid, it will be parallel to the bases and its length will be the average of the length of the bases.
– The intersection point of the diagonals is collinear to the midpoints of the two opposite sides.
– If there is a trapezoid with sides a, b, c and d and diagonals p and q, the following equation will be true: p2+q2= c2+d2+2ab
Turn and Talk Compare your drawing from Task 2 with a classmate. Do both drawings belong to the same group? Why or why not?
Answer:
Question 3.
Look at the shapes.
A. What name do all the quadrilaterals in this group share?
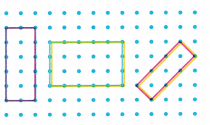
Answer: Rectangle.
Definition and the properties:
A Rectangle is a four sided-polygon, having all the internal angles equal to 90 degrees. The two sides at each corner or vertex, meet at right angles. The opposite sides of the rectangle are equal in length which makes it different from a square.
– A rectangle is a type of quadrilateral that has its parallel sides equal to each other and all four vertices are equal to 90 degrees. Hence, it is also called an equiangular quadrilateral. Since, the opposite sides are equal and parallel, in a rectangle, therefore, it can also be termed as a parallelogram.
The shape of the rectangle:
A rectangle is a two-dimensional flat shape. In an XY plane, we can easily represent a rectangle, where the arms of x-axis and y-axis show the length and width of the rectangle, respectively.
Rectangular shaped objects: The most common everyday things or objects we see and are rectangular in shape is Television, computer screen, notebook, mobile phones, CPU, Notice boards, Table, Book, TV screen, Mobile phone, Wall, Magazine, Tennis court, etc.
– It has four sides and four vertices
– Each vertex has an angle equal to 90 degrees
– The opposite sides are equal and parallel
– Diagonals bisect each other
– Perimeter is equal to twice some of its length and breadth
– The area is equal to the product of its length and breadth
– It’s a parallelogram with four right angles.
– Sum of all interior angles equal to 360 degrees
B. Draw a shape that belongs to this group.

Answer: I can draw a parallelogram because It is a quadrilateral with two pairs of parallel sides. The opposite sides are parallel and equal in length. The opposite angles are equal in measure.
– In the parallelogram, ABCD, side AB is parallel to side CD and side AD is parallel to side BC. Also, the two diagonals formed to intersect each other at the midpoints. As in the figure given below, E is the point where both the diagonals meet.
So, Length AE = EC, & Length BE = ED.
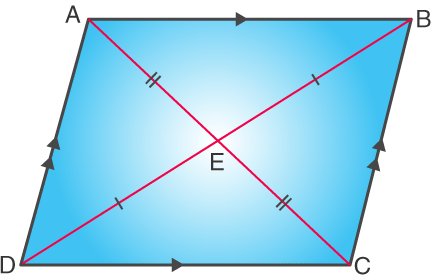
C. What attributes do all the shapes in this group share?
Answer:
Attribute of parallelogram:
If a quadrilateral has a pair of parallel opposite sides, then it’s a special polygon called Parallelogram. The properties of the parallelogram are as follows:
– The opposite sides are parallel and congruent
– The opposite angles are congruent
– The consecutive angles are supplementary
– If any one of the angles is a right angle, then all the other angles will be at a right angle
– The two diagonals bisect each other
– Each diagonal bisects the parallelogram into two congruent triangles
– The Sum of the square of all the sides of a parallelogram is equal to the sum of the square of its diagonals. It is also called parallelogram law.
Question 4.
Look at the shapes.
A. Draw shape A that belongs to the group.
Answer: We can draw quadrilateral, rectangles also
A quadrilateral has:
– four sides (edges)
– four vertices (corners)
– interior angles that add to 360 degrees
B. Draw shape B that has 2 right angles and exactly one pair of parallel sides.
Answer: We can draw trapezium. It is a quadrilateral with one pair of opposite parallel sides.
There are certain properties of trapezoids that identify them as trapezoids:
– The base angles and the diagonals of an isosceles trapezoid are equal.
– If you draw a median on a trapezoid, it will be parallel to the bases and its length will be the average of the length of the bases.
– The intersection point of the diagonals is collinear to the midpoints of the two opposite sides.
– If there is a trapezoid with sides a, b, c and d and diagonals p and q, the following equation will be true: p2+q2= c2+d2+2ab
Turn and Talk What quadrilateral group do both shape A and shape B above belong to? Explain.
Answer: square and trapezium.
Square: It is a quadrilateral in which all the sides and angles are equal. Every angle is a right angle (i.e. 90° each). The pairs of opposite sides are parallel to each other.
Trapezium: It is a quadrilateral with one pair of opposite parallel sides. In the trapezium, ABCD, side AB is parallel to side CD.
Check Understanding
Draw and name the quadrilateral.
Question 1.
4 sides of equal length, no right angles

Answer: Parallelogram

A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. Sum of all the interior angles equals 360 degrees.
– The opposite sides are parallel and congruent
– The opposite angles are congruent
– The consecutive angles are supplementary
– If any one of the angles is a right angle, then all the other angles will be at a right angle
– The two diagonals bisect each other
– Each diagonal bisects the parallelogram into two congruent triangles
– The sum of the square of all the sides of a parallelogram is equal to the sum of the square of its diagonals. It is also called parallelogram law
Question 2.
2 pairs of parallel sides, no right angles

Answer: Parallelogram

A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. Sum of all the interior angles equals 360 degrees.
– The opposite sides are parallel and congruent
– The opposite angles are congruent
– The consecutive angles are supplementary
– If any one of the angles is a right angle, then all the other angles will be at a right angle
– The two diagonals bisect each other
– Each diagonal bisects the parallelogram into two congruent triangles
– The sum of the square of all the sides of a parallelogram is equal to the sum of the square of its diagonals. It is also called parallelogram law
On Your Own
Reason Draw a quadrilateral that does not belong to the group. Then explain why it does not belong.
Question 3.

Answer: I would draw a trapezoid.

A trapezoid is a quadrilateral with at least one pair of opposite parallel sides.
A trapezoid is a quadrilateral with exactly one pair of opposite parallel sides.
In fact, what is up with trapezoids? As we saw, there’s some debate about the exact definition, but it always involves this parallel opposite sides idea. But we don’t need parallelism to define any of the other quadrilaterals. In fact, this points to a deeper fact: trapezoids don’t even have to exist! In spherical geometry, there are no parallel lines. So, therefore, there are no trapezoids in spherical geometry.
Question 4.

Answer: I would draw a trapezoid.

A trapezoid is a quadrilateral with at least one pair of opposite parallel sides.
A trapezoid is a quadrilateral with exactly one pair of opposite parallel sides.
In fact, what is up with trapezoids? As we saw, there’s some debate about the exact definition, but it always involves this parallel opposite sides idea. But we don’t need parallelism to define any of the other quadrilaterals. In fact, this points to a deeper fact: trapezoids don’t even have to exist! In spherical geometry, there are no parallel lines. So, therefore, there are no trapezoids in spherical geometry.
Question 5.
Reason Rhombus Billboards makes all their signs in the shape of a rhombus. On April Fool’s Day, Rhombus Billboards makes a quadrilateral sign that is not a rhombus. Draw a sign that the company might make. Explain why the shape you drew does not belong in the group.

Answer:
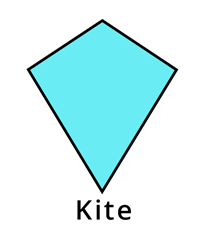
A kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other and only one pair of opposite angles are equal. All sides of a rhombus are equal and opposite angles are equal. So, all kites are not rhombuses.
I’m in a Learning Mindset!
Do I share and accept strategies from others? What are some examples?
Answer: Yes, that is a great idea. I think it is very important to be open-minded.
Example: I think we all need to be more accepting of others. It is hard when you are in a situation where you are being rejected or bullied.
– Sometimes people try to stay in denial when they face a tough situation. However, the longer you try to avoid the problem, the longer it will take to address it. Acknowledge the situation exists, regardless of how you feel about it. Be prepared to face the situation head-on so you can get through it. Even if you can’t change the situation, acknowledging it can help you accept it and move on.