We included HMH Into Math Grade 3 Answer Key PDF Module 2 Lesson 5 Find the Area of Combined Rectangles to make students experts in learning maths.
HMH Into Math Grade 3 Module 2 Lesson 5 Answer Key Find the Area of Combined Rectangles
I Can break apart a figure made up of combined rectangles to find the area, I can multiply and add to find the area.
Spark Your Learning
Mrs. Lyon draws a design to represent a hallway in her school.

Show two ways to find the area of the hallway. Each unit square is 1 square foot.
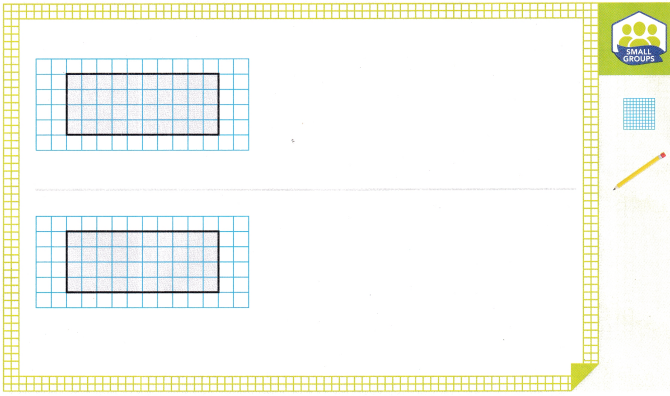
What is the area of the hallway? _____
Answer:
Explanation:
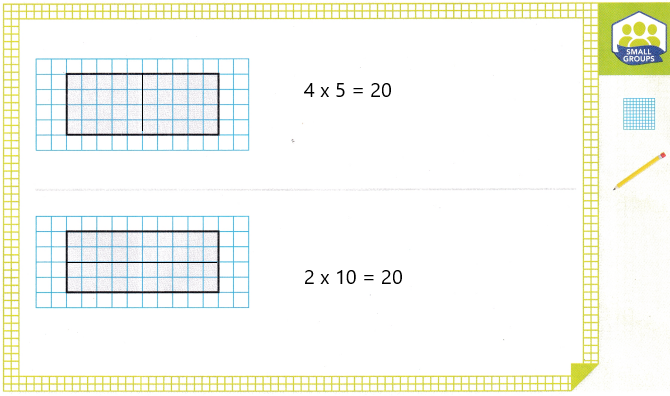
I drew the rectangles in half
Each unit square is 1 square foot
One way is dividing into 4 rows of 5 unit squares
4 x 5 = 20
Other way is dividing into 2 rows of 10 unit squares
2 x 10 = 20
So, the area of the halfway is 20 square feet.
Turn and Talk Which way that you used to find the area was easier?
Answer:
The way where i divide it in equal column is easy to find.
Build Understanding
1. Mazie draws the floor plan below to represent a music room so that she can help organize the instruments. What is the area of the music room floor?

A. What smaller figures do you see in the floor plan?
____________________________
B. How can you find the area of these smaller figures?
____________________________
____________________________
Show one way to find the area of the music room floor.
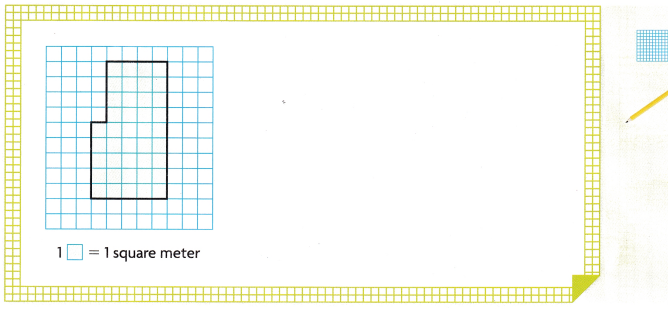
C. What equation can you write to combine the areas of the smaller rectangles?
____________________________
D. What is the area of the music room floor?
____________________________
Answer:

Explanation:
Mazie draws the floor plan below to represent a music room so that she can help organize the instruments
I can see 2 small squares in the floor plan
Multiply to find the area of the squares
1st square: 4 x 4 = 16
2nd square: 5 x 5 = 20
Add 16 and 20
16 + 20 = 36
1 unit square is 1 square meter
So, the area of the floor is 36 square meters.
Step It Out
2. Celia draws a diagram of a figure she plans to use to paint a mural. What is the area of the mural?
A. Draw a vertical or horizontal line to break apart the figure into smaller rectangles.
B. Write a multiplication equation for each rectangle to find the area.
___ × ___ = ____
___ × ___ = ____
C. Add the products to find the total area.
___ + ___ = ___
The area of the mural is ___.
Answer:
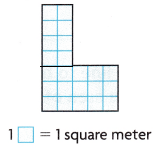
Area = 23 square meters
Explanation:
Celia draws a diagram of a figure she plans to use to paint a mural
I divided the mural into 2 smaller rectangles
Area of the rectangles are
4 x 2 = 8
3 x 5 = 15
8 + 15 = 23
1 unit square is 1 square meter.
So, the area of the mural is 23 square meters.
Turn and Talk If you broke apart the figure into different rectangles, would the total area change? Explain.
Answer:
No, if we divide the figure in another way the area does not change as the figure is same.
Check Understanding Math Board
Question 1.
What is the area of the figure? Draw a vertical or horizontal line to break apart the figure into
smaller rectangles. Complete the equations.
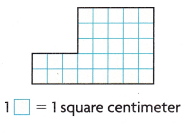
___ × ___ = ____
___ × ___ = ____
___ + ___ = ____
Area = ___ square centimeters
Answer:
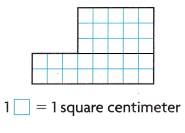
Explanation:
Area of small rectangles
3 x 5 = 15
2 x 8 = 16
15 + 16 = 31
1 unit square is 1 square centimeter
Area = 31 square centimeters.
On Your Own
Question 2.
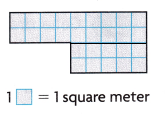
Attend to Precision Mr. Evans draws this diagram of a rug for his family room and office. What is the area of the rug?
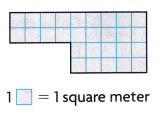
Answer:
Explanation:
Area of small rectangles
2 x 9 = 18
2 x 5 = 10
18 + 10 = 28
1 unit square is 1 square meter
Area = 28 square meters
Draw a line to break apart the figure into rectangles. Find the area of the figure.
Question 3.
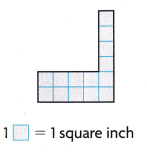
Area = ___ square inches
Answer:
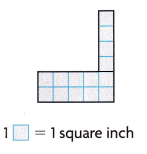
Explanation:
Area of small rectangles
4 x 1= 4
2 x 5 = 10
4 + 10 = 14
1 unit square is 1 square inch
Area = 14 square inches
Question 4.
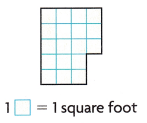
Area = ___ square feet
Answer:
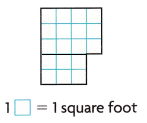
Explanation:
Area of small rectangles
3 x 4 = 12
2 x 3 = 6
12 + 6 = 18
1 unit square is 1 square foot
Area = 18 square feet
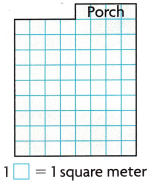
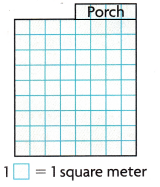
Question 5.
STEM Building architects often use combined rectangles when designing buildings. How does adding a porch to this tiny house change the total area of the design? What is the total area of the design?
Answer:
Explanation:
Building architects often use combined rectangles when designing buildings
Area of small rectangles
1 x 3 = 3
9 x 8 = 72
3 + 72 = 75
1 unit square is 1 square meter
So, the total area of the design is 75 square meters.
I’m in a Learning Mindset!
What strategy did I use to solve Problem 2?
____________________________
____________________________