We included HMH Into Math Grade 3 Answer Key PDF Module 16 Lesson 3 Recognize and Generate Equivalent Fractions to make students experts in learning maths.
HMH Into Math Grade 3 Module 16 Lesson 3 Answer Key Recognize and Generate Equivalent Fractions
I Can represent a fraction with equal parts that are smaller or larger in size than the equal parts of an equivalent fraction.
Spark Your Learning
Meghan wants to save some of the lasagna she makes for her cousin Jeremy. She divides the pan of lasagna into fourths and saves \(\frac{2}{4}\) of the pan for Jeremy.

Can you think of two other ways Meghan can divide the lasagna into equal-sized smaller or larger parts and still save the same amount for Jeremy?
Show how to divide the lasagna for each pan. Shade the parts that Meghan saves for Jeremy. Explain how you know that Jeremy will get the same amount of lasagna for each pan.
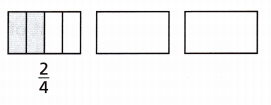
Answer:
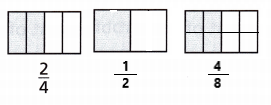
Explanation:
I drew parts for the lasagna in two other ways
Even though the parts are big and small, the part of lasagna Megan saves for Jeremy is same.
So, Jeremy will get the same amount of lasagna for each pan.
Turn and Talk How can you check to see if two fractions are equivalent?
Answer:
We can simplify the fractions if all the fractions are equal they get to same answer after simplification.
Build Understanding
Question 1.
Rico’s band eats pizza after band practice each week. On Friday, the band eats \(\frac{6}{8}\) of a cheese pizza. The next week, the band eats the same amount of a same-sized vegetable pizza cut into 4 equal pieces. What fraction of the vegetable pizza does the band eat?

Show one way to solve the problem.
A. How can you draw lines to divide the two pizzas? Into how many pieces will you divide each pizza?
Answer:
I will divide the cheese pizza into 8 parts by drawing three lines, i will divide the vegetable pizza into 4 pats by drawing 2 lines.
B. How can you shade the pizzas to show how much the band eats?
Answer:
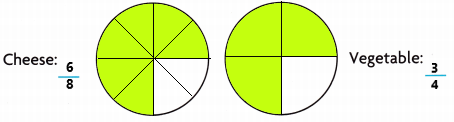
C. What fraction can you write for the amount of each pizza that the band eats? Label each pizza to show the fraction of each pizza the band eats. How do these fractions compare?
Answer:
The band eats \(\frac{6}{8}\) of cheese pizza and \(\frac{3}{4}\) of vegetable pizza, both qre equivalent fractions.
D. Write the fractions. Write >, <, or =.
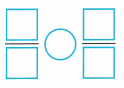
The band eats _________ of the vegetable pizza.
Answer:
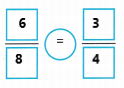
Explanation:
The band eats \(\frac{3}{4}\) of vegetable pizza.
Turn and Talk Two fractions are equivalent. The first fraction has a greater denominator. What does that tell you about the numerator of the first fraction?
Answer:
Question 2.
Lea runs \(\frac{3}{2}\) mile. Roxie runs the same distance on a track laid out in fourths of a mile. How far does Roxie run?

A. Complete the number line.
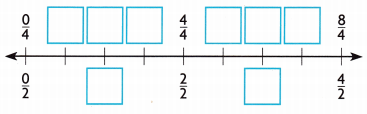
Answer:
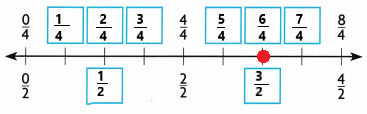
B. Locate and draw a point on the number line to show how far Lea and Roxie run. Write the equivalent fraction.
\(\frac{3}{2}\) mile = ___________
Answer:
I drew a point on the number line
An equivalent fraction for \(\frac{3}{2}\) is \(\frac{6}{4}\).
Question 3.
Draw circles to show equal groups. Find equivalent fractions for the shaded area of the shapes. Write the fractions.

Answer:
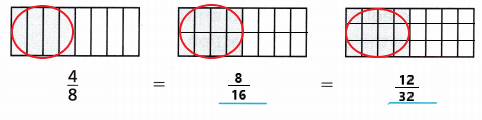
Explanation:
I drew circles to show the equal groups
The fractions are \(\frac{4}{8}\), \(\frac{8}{16}\) and \(\frac{12}{32}\).
Check Understanding
Question 1.
Circle equal groups to find an equivalent fraction for the shaded area:
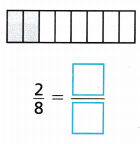
Answer:
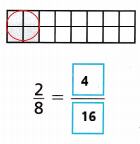
Explanation:
An equivalent fraction for the shaded area is \(\frac{4}{16}\).
Question 2.
Draw a point on the number line to find an equivalent fraction.
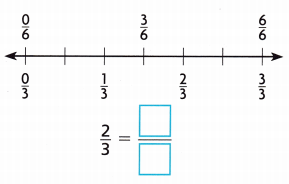
Answer:
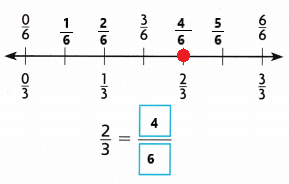
Explanation:
I marked the point \(\frac{2}{3}\) on the number line
An equivalent fraction for \(\frac{2}{3}\) is \(\frac{4}{6}\).
On Your Own
Question 3.
Use Structure Robert eats \(\frac{1}{3}\) of a granola bar. Ken eats the same amount of his granola bar. Both granola bars are the same size. Ken divides his bar into sixths. What fraction of a granola bar does Ken eat? Show how much Ken and Robert eat. Write an equivalent fraction.

Answer:

Explanation:
Ken and Robert eat the bar about a fraction of \(\frac{1}{3}\).
An equivalent fraction for \(\frac{1}{3}\) is \(\frac{2}{6}\).
Question 4.
Locate and draw a point on the number line. Then write the equivalent fraction.
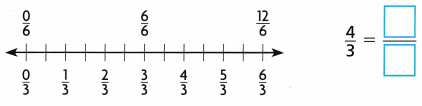
Answer:
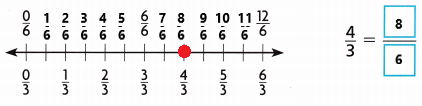
Explanation:
An equivalent fraction for \(\frac{4}{3}\) is \(\frac{8}{6}\).
I marked the point \(\frac{4}{3}\) on the number line.
Question 5.
Shade to show an equivalent fraction on the visual model. Then write the equivalent fraction.

Answer:

Explanation:
An equivalent fraction for \(\frac{3}{6}\) is \(\frac{1}{2}\).
Question 6.
STEM A wheel and an axle turn together in the direction shown. One wheel has 4 spokes and makes \(\frac{3}{4}\) of a turn. The other wheel has 8 spokes. Shade to show how far the 8-spoke wheel turns. Write the equivalent fraction.
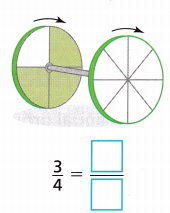
Answer:
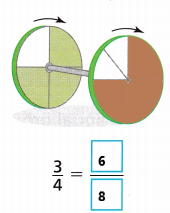
Explanation:
An equivalent fraction for \(\frac{3}{4}\) is \(\frac{6}{8}\).
I’m in a Learning Mindset!
How can a visual model help me understand how to generate equivalent fractions?
Answer: