Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts

We included HMH Into Math Grade 3 Answer Key PDF Module 16 Lesson 1 Represent Equivalent Fractions with Smaller Parts to make students experts in learning maths.

HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts

I Can represent a fraction with equal parts that are smaller in size than the equal parts of an equivalent fraction.

Spark Your Learning

Kyra folds a sheet of paper in half and shades 1 of the 2 sections. Julio folds Kyra’s sheet in half again. Kyra says $\frac{1}{2}$ of the sheet is shaded. Julio says $\frac{2}{4}$ of the sheet is shaded. Who is correct?
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 1$
Show and explain your answer.
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 2$
Answer:

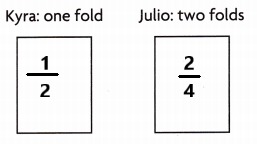
Explanation:
Both are correct as the fraction Kyra and Julio told are equivalent fractions.

Turn and Talk After Julio makes his fold, Kyra folds the paper in half one more time. What fraction is now shaded?
Answer:

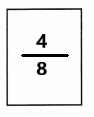
Explanation:
$\frac{4}{8}$ fraction is now shaded.

Build Understanding

Question 1.
Tia folds a square sheet of paper into fourths. She shades $\frac{3}{4}$ of the paper red.
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 3$
Show how Tia’s paper might look in the workspace on the left.
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 4$
Answer:

Tia takes the folded sheet of paper and folds it again to make eighths.

Show how Tia’s paper might look now in the workspace above on the right.
A. What fraction of the paper is now shaded red?
Answer:
The fraction of paper now shaded in red is $\frac{6}{8}$.

B. How does $\frac{3}{4}$ compare to the fraction Tia made by folding the paper into eighths?
Answer:
The fraction $\frac{3}{4}$ changes into $\frac{6}{8}$ fraction Tia made by folding the paper into eighths.

Turn and Talk What happens to the size and number of the equal parts each time Tia folds the paper?
Answer:
The size and number of equal parts gets doubled each time Tia folds the paper.

Question 2.
Alvin folds a strip of paper into thirds and shades $\frac{2}{3}$. Then Alvin folds the same strip again into sixths. Show Alvin’s strip folded into thirds and sixths.
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 5$
Answer:

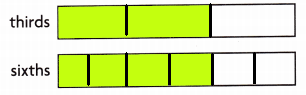
Explanation:
I have shown the strip of paper that Alvin folds into thirds and sixths and labeled the fraction $\frac{2}{3}$.
Connect to Vocabulary
Two or more fractions that name the same amount or distance on a number line are called equivalent fractions.

A. Divide the number line to show thirds and sixths. Label the fractions on the number line. Then draw a point to show the part of the strip Alvin shaded.
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 6$
Answer:

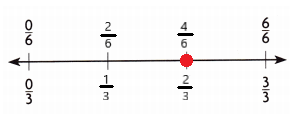
Explanation:
I labeled the fraction $\frac{2}{3}$.

B. What fraction in sixths is equivalent to $\frac{2}{3}$? How do you know that the two fractions are equivalent?
Answer:
A fraction $\frac{4}{6}$ in sixths is equivalent to $\frac{2}{3}$.

Turn and Talk Can two fractions with a different number of equal parts be equivalent? Explain.
Answer:

Check Understanding

Question 1.
Shade to show $\frac{1}{4}$. Then draw a line to show an equivalent fraction.
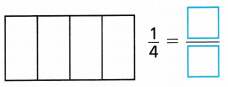
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 7$
Answer:

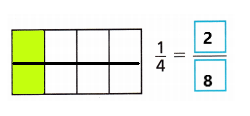
Explanation:
I shaded the $\frac{1}{4}$ part
An equivalent fraction for $\frac{1}{4}$ is $\frac{2}{8}$.

Question 2.
Draw a point to show $\frac{1}{2}$. Then write the equivalent fraction.
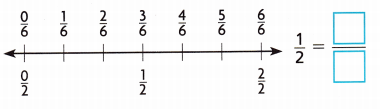
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 8$
Answer:

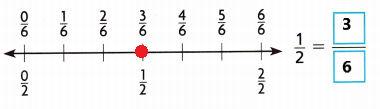
Explanation:
An equivalent fraction for $\frac{1}{2}$ is $\frac{3}{6}$.

On Your Own

Question 3.
Use Tools Brian shades $\frac{1}{2}$ of a circle green. Show an equivalent fraction on the same-sized circle.
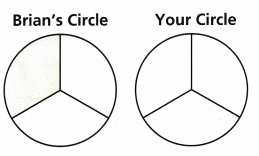
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 9$
Write the equivalent fraction. $\frac{1}{3}$ = $HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 10$
Answer:

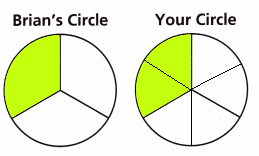
Explanation:
$\frac{1}{3}$ =

Explain why the fractions shown by Brian’s circle and your circle are equivalent.
Answer:
The fraction shown by Brain’s circle and my circle are equivalent as both the circles are same sized circles.

Locate and draw a point on the number line for the fraction. Then write the equivalent fraction in the equation and on the number line.

Question 4.
$\frac{2}{4}$ = $HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 10$
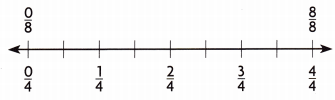
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 11$
Answer:

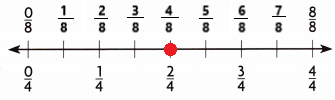
Explanation:
$\frac{2}{4}$ =

Question 5.
$\frac{1}{3}$ = $HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 10$
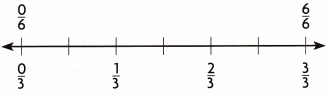
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 12$
Answer:

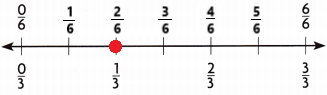
Explanation:
$\frac{1}{3}$ = .

Question 6.
Reason Explain why $\frac{3}{3}$ = $\frac{4}{4}$ for the same-sized whole. Draw to justify your answer.
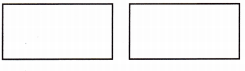
$HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts 13$

Answer:

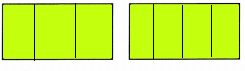
Explanation:
The shaded part in the left is $\frac{3}{3}$ adn the shaded part in the right is $\frac{4}{4}$.
In both the pictures the shaded part is same.
Therefore, $\frac{3}{3}$ = $\frac{4}{4}$ for the same-sized whole.

I’m in a Learning Mindset!

What tools can I use to solve problems with equivalent fractions?
Answer:

HMH Into Math Grade 3 Module 16 Lesson 1 Answer Key Represent Equivalent Fractions with Smaller Parts

Leave a Comment Cancel Reply