We included HMH Into Math Grade 3 Answer Key PDF Module 15 Lesson 4 Use Reasoning Strategies to Compare Fractions to make students experts in learning maths.
HMH Into Math Grade 3 Module 15 Lesson 4 Answer Key Use Reasoning Strategies to Compare Fractions
I Can use different reasoning strategies to compare fractions.
Spark Your Learning
Nora picks \(\frac{3}{4}\) pound of cherries. Ned picks \(\frac{7}{8}\) pound of cherries. Who picks the greater amount of cherries?
Show your strategy for comparing the fractions.
Answer:
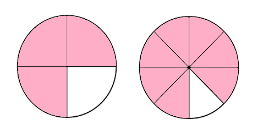
Explanation:
Nora picks \(\frac{3}{4}\) pound of cherries. Ned picks \(\frac{7}{8}\) pound of cherries.
Compare both the fractions, as the shaded area of Ned is more we can say that Ned picked the greater amount of cherries.
Turn and Talk What do you notice about the size of the missing piece in each of the fractions you compared? How can you use the missing piece and reasoning to compare the fractions?
Answer:
In the first fraction one fourth of the piece is missing and the second fraction 1 eighth of the piece is missing. As one eighth is less than one fourth we can say that fraction \(\frac{7}{8}\) is greater than \(\frac{3}{4}\).
Build Understanding
Question 1.
Ian’s granola bar recipe calls for \(\frac{2}{3}\) cup of oats. Sadie’s recipe uses \(\frac{3}{4}\) cup of oats. Whose recipe uses fewer oats?
Show how to compare \(\frac{2}{3}\) and \(\frac{3}{4}\).
Answer:
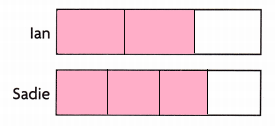
A. What fractions represent the missing piece of each whole?
Answer:
\(\frac{1}{3}\), \(\frac{1}{4}\) are the fractions that represents the missing piece of each whole.
B. Do the missing pieces have the same numerator or the same denominator?
Answer:
The missing pieces have the same numerator.
C. How can you use the size of the missing pieces to compare \(\frac{2}{3}\) and \(\frac{3}{4}\)?
Answer:
If size of the missing piece is more then that fraction will be smaller than the other fraction.
D. Whose recipe uses fewer oats?
Answer:
Ian’s recipe uses fewer oats as the missing part of the Ian’s recipe is more.
Turn and Talk For you, which is most important for comparing fractions—the numerators, the denominators, or your visual models?
Answer:
In case of different numerators and denominators visual models will be easy to compare the fractions.
Step It Out
Question 2.
Beth’s glass of orange juice is \(\frac{3}{8}\) full. Leo’s glass is \(\frac{3}{4}\) full. Both glasses hold the same amount. Whose glass has more juice? Choose a strategy to compare the fractions.
A. To compare the fractions, which strategy works best? Explain.
Answer:
In the fractions with same numerator, the fraction with smaller denominator is greater.
This is the best strategy to compare the fractions.
B. Which fraction is greater? Whose glass has more juice? Explain your answer.
Answer:
Here the numerators are same so, the smaller denominator will be the greater fraction
So, \(\frac{3}{4}\) is greater than \(\frac{3}{8}\)
Beth’s glass of orange juice is \(\frac{3}{8}\) full
Leo’s glass is \(\frac{3}{4}\) full
Both glasses hold the same amount
Therefore, Leo’s glass has more juice.
Check Understanding
Question 1.
Trent can hold his breath for \(\frac{4}{6}\) minute. Is this greater than or less than \(\frac{2}{6}\) minute?
Draw to show your reasoning.
Answer:
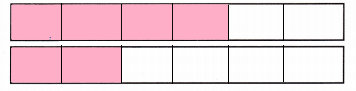
Explanation:
Trent can hold his breath for \(\frac{4}{6}\) minute
In the above drawing, i shaded the fractions
So, as shown \(\frac{4}{6}\) minute is greater than \(\frac{2}{6}\).
Compare. Write <, >, or =. Write the strategy you used.
Question 2.
\(\frac{5}{6}\) 
\(\frac{2}{3}\)
Answer:
\(\frac{5}{6}\) 
\(\frac{2}{3}\)
Explanation:
The fraction with smaller missing piece is greater
In the above fractions, \(\frac{5}{6}\) leaves smaller missing piece than \(\frac{2}{3}\).
So, \(\frac{5}{6}\) \(\frac{2}{3}\)
Question 3.
\(\frac{3}{8}\) \(\frac{3}{6}\)
Answer:
\(\frac{3}{8}\) 
\(\frac{3}{6}\)
Explanation:
In fractions with same numerator, the fractions with smaller denominator is greater fraction
\(\frac{3}{6}\) has smaller denominator
So, \(\frac{3}{8}\) \(\frac{3}{6}\).
Question 4.
\(\frac{3}{4}\) \(\frac{2}{4}\)
Answer:
\(\frac{3}{4}\) 
\(\frac{2}{4}\)
Explanation:
In fractions with same denominator, the fraction with greater numerator is greater fraction
\(\frac{3}{4}\) has greater numerator
So, \(\frac{3}{4}\) \(\frac{2}{4}\).
On Your Own
Question 5.
Reason On a Spelling test, Diane spells \(\frac{5}{6}\) of the words correctly. Bill spells \(\frac{4}{5}\) of the words correctly. Explain why the missing pieces strategy should work for comparing these the fractions. Which fraction is greater? How do you know?
Answer:
\(\frac{5}{6}\) is greater
Explanation:
On a Spelling test, Diane spells \(\frac{5}{6}\) of the words correctly
Bill spells \(\frac{4}{5}\) of the words correctly
As any the numerators or denominators are not same, the missing pieces strategy should work for comparing these fractions
In the fraction \(\frac{5}{6}\), the missing piece is smaller so, the fraction is greater
Therefore, \(\frac{5}{6}\) is greater than \(\frac{4}{5}\).
Compare. Write <, >, or =. Write the strategy you used.
Question 6.
\(\frac{1}{5}\) \(\frac{1}{8}\)
Answer:
\(\frac{1}{5}\) \(\frac{1}{8}\)
Explanation:
In fractions with same numerator, the fractions with smaller denominator is greater fraction
\(\frac{1}{5}\) has smaller denominator
So, \(\frac{1}{5}\) \(\frac{1}{8}\).
Question 7.
\(\frac{3}{4}\) \(\frac{5}{4}\)
Answer:
\(\frac{3}{4}\) \(\frac{5}{4}\)
Explanation:
In fractions with same denominator, the fraction with greater numerator is greater fraction
\(\frac{5}{4}\) has greater numerator
So, \(\frac{3}{4}\) \(\frac{5}{4}\).
Question 8.
\(\frac{8}{9}\) \(\frac{3}{4}\)
Answer:
\(\frac{8}{9}\) \(\frac{3}{4}\)
Explanation:
The fraction with smaller missing piece is greater
In the above fractions, \(\frac{8}{9}\) leaves smaller missing piece than \(\frac{3}{4}\).
So, \(\frac{8}{9}\) \(\frac{3}{4}\).
Question 9.
Open-Ended Write and solve a word problem that uses the same numerator strategy to compare two fractions. Include a visual model with your problem.
Answer:
In a race John ran a distance of \(\frac{3}{5}\) of the race and Sid ran a distance of \(\frac{3}{8}\) of the same race.
Who ran the long distance in the race.
Explanation:
In fractions with same numerator, the fractions with smaller denominator is greater fraction
\(\frac{3}{5}\) has smaller denominator
So, \(\frac{3}{5}\) is greater than \(\frac{3}{8}\) .
I’m in a Learning Mindset!
Which of the following helped me best understand how to compare fractions in this lesson: comparing same denominators, same numerators, drawing a fraction model, or visualizing an image in my head? Explain.
Answer: