We included HMH Into Math Grade 3 Answer Key PDF Module 15 Lesson 1 Compare Fractions Using Concrete and Visual Models to make students experts in learning maths.
HMH Into Math Grade 3 Module 15 Lesson 1 Answer Key Compare Fractions Using Concrete and Visual Models
I Can use concrete and visual models to compare fractions.
Spark Your Learning
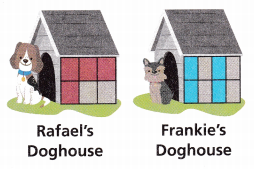
Rafael and Frankie each paint 4 equal parts of their doghouse walls. Each wall is the same size. Who uses more paint?
Show one way to find who uses more paint.
Answer:
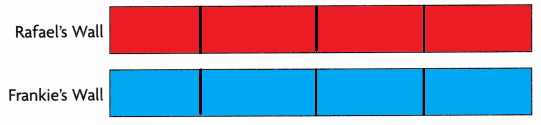
Explanation:
Rafael and Frankie each paint 4 equal parts of their doghouse walls
Each wall is of same size
So, Both Rafael and Frankie uses same amount of paint as they both painted same area of wall.
Turn and Talk Toby paints 4 of 6 sections on a small doghouse wall. Nan paints 4 of 6 sections on a large doghouse wall. Toby says that he and Nan used the same amount of paint because \(\frac{4}{6}\) = \(\frac{4}{6}\). Does Toby’s statement make sense? Why or why not?
Answer:
No, Toby’s statement is not correct
Explanation:
Toby paints 4 of 6 sections on a small doghouse wall
Nan paints 4 of 6 sections on a large doghouse wall
Toby says that he and Nan used the same amount of paint because \(\frac{4}{6}\) = \(\frac{4}{6}\)
As the walls are not of same size, the parts of both dog houses will be unequal.
So, Toby’s statement is not correct
Nan paints more than Toby.
Build Understanding
Question 1.
The Jasper City Parks Department marks off \(\frac{3}{4}\) of its South Rink for Family Skating. In the North Rink, \(\frac{3}{8}\) of the space is used for Family Skating. Both rinks are the same size and shape.

Use a concrete or visual model to show and compare the parts of the rinks that are used for Family Skating.
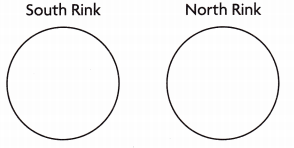
Answer:
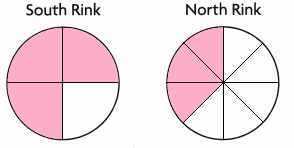
A. Which rink has a larger area for Family Skating? How do you know?
Answer:
South rink has a larger area for family skating
Explanation:
The Jasper City Parks Department marks off \(\frac{3}{4}\) of its South Rink for Family Skating
In the North Rink, \(\frac{3}{8}\) of the space is used for Family Skating
I shaded the fractions of north and south rinks, compared them.
Therefore, south rink has more area for family skating than the north rink as the shaded part of south rink is greater than north rink.
Connect to Vocabulary
Use these symbols to compare two fractions. means “greater than” = means “equal to”
B. Compare the fractions. \(\frac{3}{4}\) ![]() \(\frac{3}{8}\)
\(\frac{3}{8}\)
Answer:
\(\frac{3}{4}\) ![]() \(\frac{3}{8}\)
\(\frac{3}{8}\)
Explanation:
south rink has more area for family skating than the north rink as the shaded part of south rink is greater than north rink
So, \(\frac{3}{4}\) ![]() \(\frac{3}{8}\).
\(\frac{3}{8}\).
Question 2.
Use the visual model to compare \(\frac{4}{8}\) and \(\frac{5}{8}\).
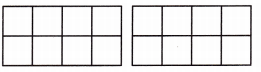
A. Shade to show \(\frac{4}{8}\) and \(\frac{5}{8}\). Which fraction has the larger amount of the whole shaded? How do you know?
Answer:
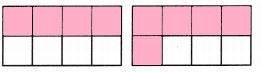
Explanation:
I shaded the fractions \(\frac{4}{8}\) and \(\frac{5}{8}\) in the above frames.
B. Write <, >, or =. \(\frac{4}{8}\) ![]() \(\frac{5}{8}\)
\(\frac{5}{8}\)
Answer:
\(\frac{4}{8}\) ![]() \(\frac{5}{8}\)
\(\frac{5}{8}\)
Explanation:
As the whole part is same that fraction will be greater whose numerator that is counted parts is more.
So, \(\frac{4}{8}\) ![]() \(\frac{5}{8}\).
\(\frac{5}{8}\).
Question 3.
Emily climbs \(\frac{2}{8}\) of the way up the climbing wall. Ryan climbs \(\frac{2}{3}\) of the way up the wall.

A. Show how you can compare the fractions on the number lines. Label the distances.
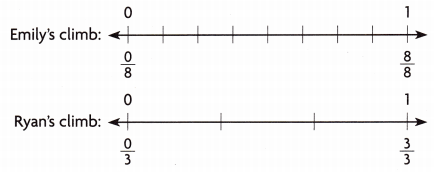
Answer:
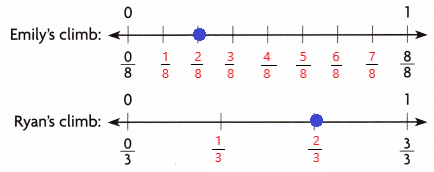
Explanation:
I labeled the distances both Emily and Ryan climbed on the number lines.
B. Write <, >, or =. \(\frac{2}{8}\) ![]() \(\frac{2}{3}\)
\(\frac{2}{3}\)
Answer:
\(\frac{2}{8}\) ![]() \(\frac{2}{3}\).
\(\frac{2}{3}\).
Explanation:
I marked the fractions \(\frac{2}{8}\) and \(\frac{2}{3}\) on the number lines and Ryan climbed more than Emily.
C. Who climbs higher? How do you know?
Answer:
Ryan climbed more
Explanation:
Ryan climbed more as shown the markings on the number lines above the distance Ryan climbed is more than the distance Emily climbed.
Turn and Talk How can the size of the equal lengths in the whole help you find which fraction is greater?
Answer:
The size of equal lengths in the whole helps us to compare the fractions easily as the whole is same the number of parts counted more will be greater.
Check Understanding
Question 1.
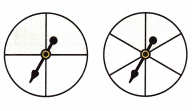
Which spinner has a larger area shaded?
Answer:
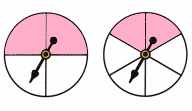
Explanation:
The shaded parts of the spinners are 2 of the whole.
Write the fractions. Write <, >, or =.
Answer:
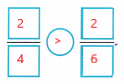
Explanation:
In the first spinner 2 parts out of 4 are shaded and in second spinner 2 parts out of 6 are shaded
So, when we compare the shaded regions we found that \(\frac{2}{4}\) > \(\frac{2}{6}\).
Shade to show each fraction. Write <, >, or =.
Question 2.
Compare \(\frac{4}{8}\) and \(\frac{4}{6}\).
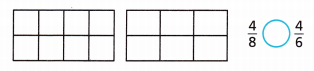
Answer:
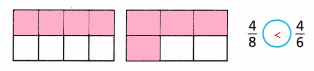
Explanation:
I shaded the fractions, compared them
Therefore, i found that \(\frac{4}{8}\) < \(\frac{4}{6}\).
Question 3.
Compare \(\frac{4}{6}\) and \(\frac{2}{6}\).
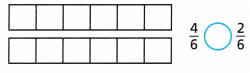
Answer:
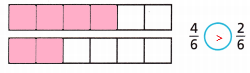
Explanation:
I shaded the fractions, compared them
Therefore, i found that \(\frac{4}{6}\) > \(\frac{2}{6}\).
On Your Own
Question 4.
Social Studies Tim compared total votes for voters aged 18-24. In a 2016 election, \(\frac{2}{8}\) of people aged 18-24 voted. In 2018, \(\frac{2}{6}\) of the same age group voted. In both elections, about the same number of votes were counted. In which election did more people aged 18-24 vote? Use a concrete or visual model to explain your answer.

Answer:
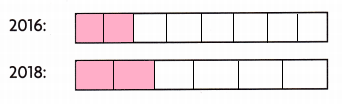
Explanation:
Social Studies Tim compared total votes for voters aged 18-24. In a 2016 election, \(\frac{2}{8}\) of people aged 18-24 voted
In 2018, \(\frac{2}{6}\) of the same age group voted
In both elections, about the same number of votes were counted
I drew lines and shaded the fractions, when compared both the fractions, In 2018 more more people aged 18-24 voted than in the year 2016.
Question 15.
Attend to Precision Patty walks \(\frac{2}{4}\) mile on Monday and \(\frac{3}{4}\) mile on Tuesday. Show the distances on the number line. On which day does Patty walk a shorter distance? How do you know?

Answer:

Explanation:
Patty walks \(\frac{2}{4}\) mile on Monday and \(\frac{3}{4}\) mile on Tuesday
I marked the distance patty walked on day 1 and day 2
When compared both the distances, the distance Patty walked on Monday is less than the distance patty walked on Tuesday
Therefore, \(\frac{2}{4}\) < \(\frac{3}{4}\).
I’m in a Learning Mindset!
How can I share the visual or concrete models I used to compare fractions to help other students with their fraction comparisons?
Answer: