We included HMH Into Math Grade 3 Answer Key PDF Module 11 Lesson 4 Represent Rectangles with the Same Area and Different Perimeters to make students experts in learning maths.
HMH Into Math Grade 3 Module 11 Lesson 4 Answer Key Represent Rectangles with the Same Area and Different Perimeters
I Can use perimeter to compare rectangles with the same area.
Step It Out
Question 1.
Cory plans to paint a rectangular mural with the least possible border on her backyard fence. The area of the mural will be 16 square feet.

A. Show all the possible rectangular murals that Cory could make.

Think: I can count the number of units from one grid line to the next along each side of the rectangle.
Answer:

Area = 16 square feet.
B. What is the perimeter of each rectangle? Write equations.
Answer:
Explanation:
p = 2(l + w)
p = 2 x 8
p = 16
p = 2(l + w)
p = 2(2 + 8)
p = 2 x 10
p = 20
C. The least perimeter is _________.
Answer:
16 is the least perimeter.
D. To have the least possible border, Cory should make the rectangle with side lengths of __________.
Answer:
4 square feet each.
To have the least possible border, Cory should make the rectangle with side lengths of 4 square feet each.
Turn and Talk When rectangles have the same area, how do you know which will have the greatest perimeter and the least perimeter?
Answer:
By Adding the length and the width.
we can find the perimeter which have least and greatest.
Question 2.
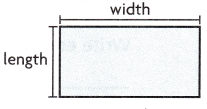
Mel plans to build a rectangular play yard for his puppies. The area of the play yard must be 12 square meters.

A. Draw all the rectangles that can represent the play yard.

Answer:

area = 12 square meters.
12 can also written as 4 x 3,3 x 4.
2 x 6 and 6 x 2
B. What is the perimeter of each play yard? Write equations.
Answer:
1) perimeter of figure1 = 14
p = 2(l + w)
p = 2 x 7
2) perimeter of figure 2 = 14
p = 2(l + w)
p = 2 x 7
3) perimeter of figure 3 = 16
p = 2(l + w)
p = 2 x 8
4) perimeter of figure 4 = 16
p = 2(l + w)
p = 2 x 8
C. The play yard that is _________ meter long and ______ meters wide will have the greatest perimeter.
Answer:
The play yard that is 2 meter long and 8 meters wide will have the greatest perimeter.
D. What is the difference between the length and width for each play yard you drew? Write equations. What do you notice?
Answer:
1) perimeter of figure1 = 14
p = 2(l + w)
p = 2 x 7
2) perimeter of figure 2 = 14
p = 2(l + w)
p = 2 x 7
3) perimeter of figure 3 = 16
p = 2(l + w)
p = 2 x 8
4) perimeter of figure 4 = 16
p = 2(l + w)
p = 2 x 8
The perimeter changes but not the area.
Check Understanding
Question 1.
Draw two different rectangles with an area of 18 square feet. Find the perimeter of each rectangle you drew.
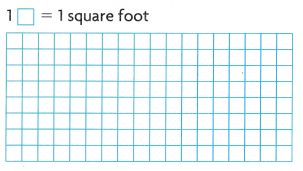
Answer:
Area = 18
Area = l x w
18 can also written as 2 x 9
and 3 x 6
Explanation:
Perimeter of first figure
p = 2(l + w)
p = 2(3 + 6)
p = 2 x 9
p = 18
p = 2(l + w)
p = 2(2 + 9)
p = 2 x 11
p = 22
On Your Own
Question 2.
Critique Reasoning Stefan draws a visual model of a rectangular patio with an area of 20 square meters. He says the perimeter cannot be more than 42 meters. Is Stefan correct? Explain. Draw to support your answer.
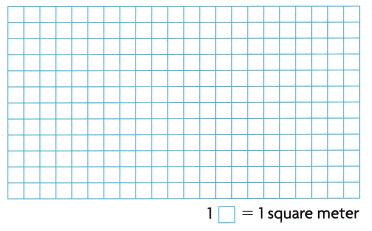
Answer:
area of 20 square meters.
a = l x w
a = 2 x 10
a = 4 x 5
p = 2(2 + 10)
p = 2 x 12
p = 24
p = 2(5 + 4)
p = 2 x 9
p = 18
Explanation:
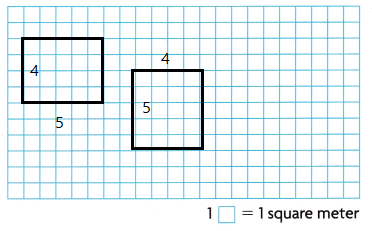
Use Repeated Reasoning Find the area and perimeter. Circle the letter of the rectangle with the greater perimeter.
Question 3.
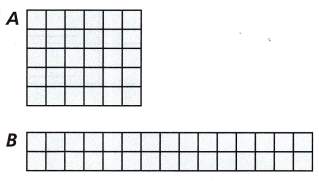
Rectangle A
Area = _________ square units
Perimeter = _________ units
Explanation:
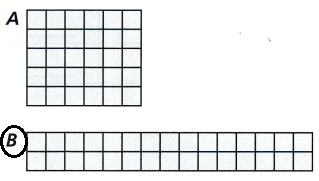
a = l x w
a = 5 x 6
a = 30
p = 2(l + w)
p = 2(5 + 6)
p = 2 x 11
p = 22
Area = 30 square units
Perimeter = 22 units
Rectangle B
Area = _________ square units
Perimeter = _________ units
Answer:
a = l x w
a = 2 x 15
a = 30
p = 2(l + w)
p = 2(2 + 15)
p = 2(17)
p = 34
Area = 30 square units
Perimeter = 34 units
Question 4.
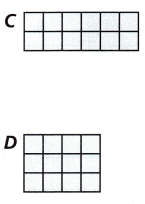
Rectangle C
Area = _________ square units
Perimeter = _________ units
Explanation:
a = l x w
a = 2 x 6
a = 12
p = 2(l + w)
p = 2(2 + 6)
p = 2 x 8
p = 16
Area = 12 square units
Perimeter = 16 units
Rectangle D
Area = _________ square units
Perimeter = _________ units
Answer:
Explanation:
a = l x w
a = 3 x 4
a = 12
p = 2(l + w)
p = 2(3 + 4)
p = 2 x 7
p = 14
Area = 12 square units
Perimeter = 14 units
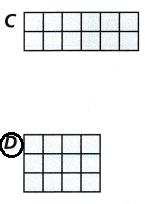
Question 5.
Open-Ended Write a word problem that matches these visual models. Solve your problem.
Answer:
Mr. Anny Bought a rectangular surface for a canvas
both has the area of 36 square feet
Help her to choose which has less perimeter.
1) figure a
p = 2(l + w)
p = 2(6 + 6)
p = 2 x 12
p = 24
2) Figure b
p = 2 (l + w)
p = 2(4 + 9)
p = 2 x 13
p = 26
Question 6.
Attend to Precision Tessa and Mick both have fenced rectangular backyards. Both backyards have the same area. Complete the table.
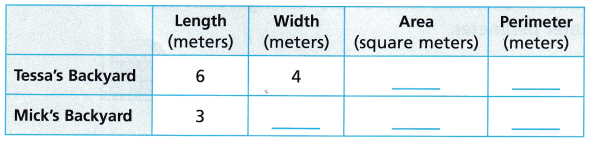
The yard that uses the least amount of fencing belongs to __________.
Answer:
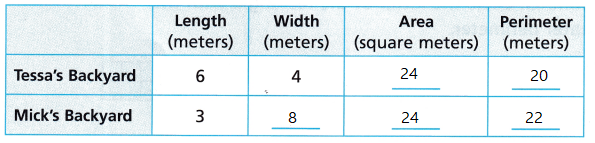
The yard that uses the least amount of fencing belongs to Tessa.
Explanation:
p = 2 x 10
p = 20
p = 2 x 11
p = 22
Question 7.
The difference between the length and width of Alan’s rectangular deck is 0 feet. The difference between the length and width of Keko’s rectangular deck is 5 feet. Both decks have the same area. Which person will need a longer railing to go around the deck? Explain.

Answer:
Keko’s rectangular deck will need a longer railing to go around the deck
Explanation:
The difference between the length and width of Alan’s rectangular deck is 0 feet.
Let us consider length and width as 6 and 6
6 – 6 = 0
area = 6 x 6
a = 36
perimeter = 2 (l + w)
p = 2 x 12
p = 24
The difference between the length and width of Keko’s rectangular deck is 5 feet.
Let us consider length and width as 9 and 4
9 – 4 = 5
a = 9 x 4
a = 36
p = 2(9 + 4)
p = 2 x 13
p = 26