Download Go Math Grade 8 Answer Key Chapter 10 Transformations and Similarity pdf for free of cost. The HMH Go Math 8th Grade Chapter 10 Transformations and Similarity Solution Key includes properties of dilations, Algebraic Representations of Dilations, and similar figures. The explanations seen in Go Math Grade 8 Answer Key Chapter 10 are prepared by the concerned subject experts. Students can overcome their difficulties with the help of the Go Math Grade 8 Chapter 10 Transformations and Similarity Answer Key.
Go Math Grade 8 Chapter 10 Transformations and Similarity Answer Key
Learning is not only important but understanding the concepts is also important for the students to enhance their skills. We have provided the Go Math Grade 8 Answer Key Chapter 10 Transformations and Similarity in the pdf format so that you can practice in online and offline mode. Thus Download Go Math Grade 8 Chapter 10 Transformations and Similarity Answer Key PDF and start your practice. The students of 8th standard can easily learn maths with the Go Math Solution Key on ccssmathanswers.com
Lesson 1: Properties of Dilations
- Properties of Dilations – Page No. 318
- Properties of Dilations – Page No. 319
- Properties of Dilations Lesson Check – Page No. 320
Lesson 2: Algebraic Representations of Dilations
- Algebraic Representations of Dilations – Page No. 324
- Algebraic Representations of Dilations – Page No. 325
- Algebraic Representations of Dilations Lesson Check – Page No. 326
Lesson 3: Similar Figures
- Similar Figures – Page No. 330
- Similar Figures – Page No. 331
- Similar Figures Lesson Check – Page No. 332
Model Quiz
Mixed Review
Guided Practice – Properties of Dilations – Page No. 318
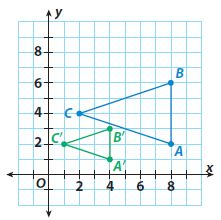
Use triangles ABC and A′B′C ′ for 1–5.
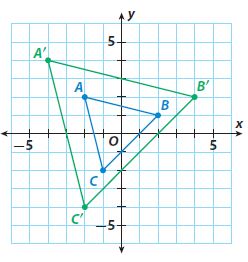
Question 1.
For each pair of corresponding vertices, find the ratio of the x-coordinates and the ratio of the y-coordinates.
ratio of x-coordinates = _______
ratio of y-coordinates = _______
ratio of x-coordinates = ____________
ratio of y-coordinates = ____________
Answer:
ratio of x-coordinates = 2
ratio of y-coordinates = 2
Explanation:
A’ = (-4, 4), A = (-2, 2);
ratio of x-coordinates = -4/-2 = 2
ratio of y-coordinates = 4/2 = 2
B’ = (4, 2), B = (2, 1);
ratio of x-coordinates = 4/2 = 2
ratio of y-coordinates = 2/1 = 2
C’ = (-2, -4), C = (-1, -2);
ratio of x-coordinates = -2/-1 = 2
ratio of y-coordinates = -4/-2 = 2
Question 2.
I know that triangle A′B′C ′ is a dilation of triangle ABC because the ratios of the corresponding x-coordinates are _______ and the ratios of the corresponding y-coordinates are _______.
Type below:
_____________
Answer:
I know that triangle A′B′C ′ is a dilation of triangle ABC because the ratios of the corresponding x-coordinates are equal and the ratios of the corresponding y-coordinates are equal.
Question 3.
The ratio of the lengths of the corresponding sides of triangle A′B′C ′ and triangle ABC equals _______.
________
Answer:
The ratio of the lengths of the corresponding sides of triangle A′B′C ′ and triangle ABC equals 2.
Question 4.
The corresponding angles of triangle ABC and triangle A′B′C ′ are _______.
Type below:
_____________
Answer:
The corresponding angles of triangle ABC and triangle A′B′C ′ are congruent.
Question 5.
The scale factor of the dilation is _______.
________
Answer:
The scale factor of the dilation is 2.
ESSENTIAL QUESTION CHECK-IN
Question 6.
How can you find the scale factor of a dilation?
Type below:
_____________
Answer:
Divide a side length of the dilated figure by the corresponding side length of the original figure.
10.1 Independent Practice – Properties of Dilations – Page No. 319
For 7–11, tell whether one figure is a dilation of the other or not. Explain your reasoning.
Question 7.
Quadrilateral MNPQ has side lengths of 15 mm, 24 mm, 21 mm, and 18 mm. Quadrilateral M′N′P′Q′ has side lengths of 5 mm, 8 mm, 7 mm, and 4 mm.
_____________
Answer:
MNPQ is not a dilation of M′N′P′Q′
Explanation:
15/5 = 3 mm
24/8 = 3 mm
21/7 = 3 mm
18/4 = 4.5 mm
The ratios of the lengths of the corresponding sides are not equal.
Therefore, MNPQ is not a dilation of M′N′P′Q′
Question 8.
Triangle RST has angles measuring 38° and 75°. Triangle R′S′T ′ has angles measuring 67° and 38°. The sides are proportional.
_____________
Answer:
Yes
Explanation:
Both Triangle S have Angle S of measures 38°, 67° and 75°. So, the corresponding ∠S are congruent.
Question 9.
Two triangles, Triangle 1 and Triangle 2, are similar.
_____________
Answer:
Yes
Explanation:
a dilation produces an image similar to the original figure
Question 10.
Quadrilateral MNPQ is the same shape but a different size than quadrilateral M′N′P′Q.
_____________
Answer:
Yes
Explanation:
The figures are similar is they are the same shape but different size SO one is a dilation of the other
Question 11.
On a coordinate plane, triangle UVW has coordinates U(20, −12), V(8, 6), and W(−24, -4). Triangle U′V′W′ has coordinates U′(15, −9), V′(6, 4.5), and W′(−18, -3).
_____________
Answer:
Yes
Explanation:
Each coordinate of Triangle U′V′W′ is 3/4 times the corresponding coordinate of Triangle UVW.
So, the scale factor of the dilation is 3/4.
Complete the table by writing “same” or “changed” to compare the image with the original figure in the given transformation.
Question 12.
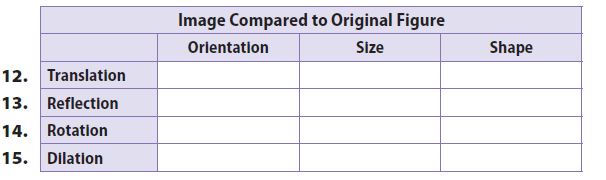
Type below:
_____________
Answer:
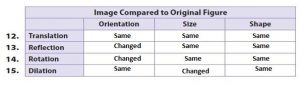
Question 16.
Describe the image of a dilation with a scale factor of 1.
_____________
Answer:
The image is congruent to the original figure
Properties of Dilations – Page No. 320
Identify the scale factor used in each dilation.
Question 17.
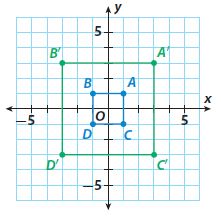
________
Answer:
3
Explanation:
A’B’/AB = 6/2 = 3
B’D’/BD = 6/2 = 3
scale factor = 3
Question 18.
\(\frac{□}{□}\)
Answer:
\(\frac{1}{2}\)
Explanation:
A’B’/AB = 2/4 = 1/2
scale factor = 1/2
FOCUS ON HIGHER ORDER THINKING
Question 19.
Critical Thinking Explain how you can find the center of dilation of a triangle and its dilation.
Type below:
_____________
Answer:
If you draw a line connecting each pair of corresponding vertices, the lines will intersect at the center of dilation
Question 20.
Make a Conjecture
a. A square on the coordinate plane has vertices at (−2, 2), (2, 2), (2, −2), and (−2, −2). A dilation of the square has vertices at (−4, 4), (4, 4), (4, −4), and (−4, −4). Find the scale factor and the perimeter of each square.
Scale factor: _________
Original perimeter: _________
Image perimeter: _________
Answer:
Scale factor: 2
Original perimeter: 16
Image perimeter: 32
Explanation:
-4/-2 =2; 4/2 = 2
Scale factor = 2
perimeter of the original square = 4 + 4 + 4 + 4 = 16
perimeter of the image = 8 + 8 + 8 + 8 = 32
Question 20.
b. A square on the coordinate plane has vertices at (−3, 3), (3, 3), (3, −3), and (−3, −3). A dilation of the square has vertices at (−6, 6), (6, 6), (6, −6), and (−6, −6). Find the scale factor and the perimeter of each square.
Scale factor: _________
Original perimeter: _________
Image perimeter: _________
Answer:
Scale factor: 2
Original perimeter: 24
Image perimeter: 48
Explanation:
-6/-3 =2; 6/3 = 2
Scale factor = 2
perimeter of the original square = 6 + 6 + 6 + 6 = 24
perimeter of the image = 12 + 12 + 12 + 12 = 48
Question 20.
c. Make a conjecture about the relationship of the scale factor to the perimeter of a square and its image.
Type below:
_____________
Answer:
The perimeter of the image is the perimeter of the original figure times the scale factor
Guided Practice – Algebraic Representations of Dilations – Page No. 324
Question 1.
The grid shows a diamond-shaped preimage. Write the coordinates of the vertices of the preimage in the first column of the table. Then apply the dilation (x, y) → (\(\frac{3}{2}\)x, \(\frac{3}{2}\)y) and write the coordinates of the vertices of the image in the second column. Sketch the image of the figure after the dilation.

Type below:
_____________
Answer:
Graph the image of each figure after a dilation with the origin as its center and the given scale factor. Then write an algebraic rule to describe the dilation.
Question 2.
scale factor of 1.5
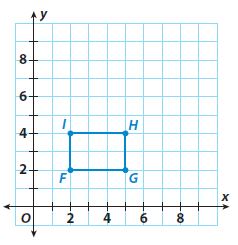
Type below:
_____________
Answer:
(x, y) -> (1.5x, 1.5y)
Explanation:
After dilation
F’ (3, 3)
G’ (7.5, 3)
H’ (7.5, 6)
I’ (3, 6)
algebraic rule: (x, y) -> (1.5x, 1.5y)
Question 3.
scale factor of \(\frac{1}{3}\)
Type below:
_____________
Answer:
(x, y) -> (1/3x, 1/3y)
Explanation:
After dilation
A’ (3, 3)
B’ (7.5, 3)
C’ (7.5, 6)
algebraic rule: (x, y) -> (1/3x, 1/3y)
ESSENTIAL QUESTION CHECK-IN
Question 4.
A dilation of (x, y) → (kx, ky) when 0 < k < 1 has what effect on the figure? What is the effect on the figure when k > 1?
Type below:
_____________
Answer:
When k is between 0 and 1, the dilation is a reduction by the scale factor k.
When k is greater than 1, the dilation is an enlargement by the scale factor k.
10.2 Independent Practice – Algebraic Representations of Dilations – Page No. 325
Question 5.
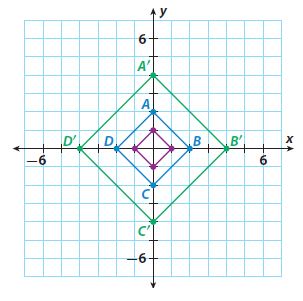
The blue square is the preimage. Write two algebraic representations, one for the dilation to the green square and one for the dilation to the purple square.
Type below:
_____________
Answer:
Green square -> (x, y) -> (2x, 2y)
Purple square -> (x, y) -> (1/2x, 1/2y)
Question 6.
Critical Thinking A triangle has vertices A(-5, -4), B(2, 6), and C(4, -3). The center of dilation is the origin and (x, y) → (3x, 3y). What are the vertices of the dilated image?
Type below:
_____________
Answer:
A'(-15, -12)
B'(6, 18)
C'(12, -9)
Explanation:
A'((3.-15), (3.-12)) -> A'(-15, -12)
B'((3. 2), (3.6)) -> B'(6, 18)
C'((3. 4), (3.-3)) -> C'(12, -9)
Question 7.
Critical Thinking M′N′O′P′ has vertices at M′(3, 4), N′(6, 4), O′(6, 7), and P′(3, 7). The center of dilation is the origin. MNOP has vertices at M(4.5, 6), N(9, 6), O′(9, 10.5), and P′(4.5, 10.5). What is the algebraic representation of this dilation?
Type below:
_____________
Answer:
(x, y) -> (2/3x, 2/3y)
Explanation:
M’N’/MN = 3/4.5 = 2/3
algebraic rule: (x, y) -> (2/3x, 2/3y)
Question 8.
Critical Thinking A dilation with center (0,0) and scale factor k is applied to a polygon. What dilation can you apply to the image to return it to the original preimage?
Type below:
_____________
Answer:
A dilation with scale factor 1/k
Question 9.
Represent Real-World Problems The blueprints for a new house are scaled so that \(\frac{1}{4}\) inch equals 1 foot. The blueprint is the preimage and the house is the dilated image. The blueprints are plotted on a coordinate plane.
a. What is the scale factor in terms of inches to inches?
Scale factor: ________
Answer:
Scale factor: 48
Explanation:
scale factor = 48
Question 9.
b. One inch on the blueprint represents how many inches in the actual house? How many feet?
________ inches
________ feet
Answer:
48 inches
4 feet
Explanation:
48 inches or 4 feet
Question 9.
c. Write the algebraic representation of the dilation from the blueprint to the house.
Type below:
_____________
Answer:
(x, y) -> (48x, 48y)
Question 9.
d. A rectangular room has coordinates Q(2, 2), R(7, 2), S(7, 5), and T(2, 5) on the blueprint. The homeowner wants this room to be 25% larger. What are the coordinates of the new room?
Type below:
_____________
Answer:
Q'(2.5, 2.5),
R'(8.75, 2.5),
S'(8.75, 6.25),
T'(2.5, 6.25)
Question 9.
e. What are the dimensions of the new room, in inches, on the blueprint? What will the dimensions of the new room be, in feet, in the new house?
Type below:
_____________
Answer:
Blueprint dimensions: 6.25 in. by 3.75 in.
House dimensions: 25ft by 15ft
Algebraic Representations of Dilations – Page No. 326
Question 10.
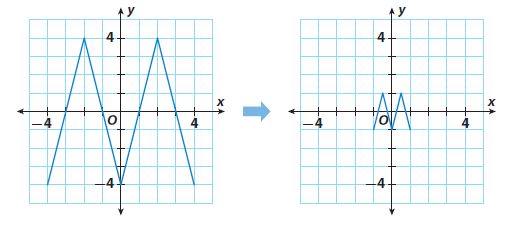
Write the algebraic representation of the dilation shown.
Type below:
_____________
Answer:
(x, y) -> (1/4x, 1/4y)
Explanation:
algebraic rule of the dilation: (x, y) -> (1/4x, 1/4y)
FOCUS ON HIGHER ORDER THINKING
Question 11.
Critique Reasoning The set for a school play needs a replica of a historic building painted on a backdrop that is 20 feet long and 16 feet high. The actual building measures 400 feet long and 320 feet high. A stage crewmember writes (x, y) → (\(\frac{1}{12}\)x, \(\frac{1}{12}\)y) to represent the dilation. Is the crewmember’s calculation correct if the painted replica is to cover the entire backdrop? Explain.
_____________
Answer:
The stage crewmember’s calculation is incorrect.
The backdrop scale factor is 1/20, not 1/12
Question 12.
Communicate Mathematical Ideas Explain what each of these algebraic transformations does to a figure.
a. (x, y) → (y, -x)
Type below:
_____________
Answer:
(x, y) → (y, -x)
90º clockwise rotation
Question 12.
b. (x, y) → (-x, -y)
Type below:
_____________
Answer:
(x, y) → (-x, -y)
180º rotation
Question 12.
c. (x, y) → (x, 2y)
Type below:
_____________
Answer:
(x, y) → (x, 2y)
vertically stretches by a factor of 2
Question 12.
d. (x, y) → (\(\frac{2}{3}\)x, y)
Type below:
_____________
Answer:
(x, y) → (\(\frac{2}{3}\)x, y)
horizontally shrinks by a factor of 2/3
Question 12.
e. (x, y) → (0.5x, 1.5y)
Type below:
_____________
Answer:
(x, y) → (0.5x, 1.5y)
horizontally shrinks by a factor of 0.5 and vertically stretches by a factor of 1.5
Question 13.
Communicate Mathematical Ideas Triangle ABC has coordinates A(1, 5), B(-2, 1), and C(-2, 4). Sketch triangle ABC and A′B′C′ for the dilation (x, y) → (-2x, -2y). What is the effect of a negative scale factor?
Type below:
_____________
Answer:
The figure is dilated by a factor of 2, but the orientation of the figure in the coordinate plane is rotated 180°
Guided Practice – Similar Figures – Page No. 330
Question 1.
Apply the indicated sequence of transformations to the square. Apply each transformation to the image of the previous transformation. Label each image with the
letter of the transformation applied.
A: (x, y) → (-x, y)
B: Rotate the square 180° around the origin.
C: (x, y) → (x – 5, y – 6)
D: (x, y) → (\(\frac{1}{2}\)x, \(\frac{1}{2}\)y)
Type below:
_____________
Answer:
Explanation:
A: (x, y) → (-x, y)
coordinates for A
(-7, -8)
(-7, -4)
(-3, -4)
(-3, -8)
B: Rotate the square 180° around the origin.
coordinates for B
(3, 4)
(3, 8)
(7, 8)
(7, 4)
C: (x, y) → (x – 5, y – 6)
coordinates for C
(-2, -2)
(-2, 2)
(2, 2)
(2, -2)
D: (x, y) → (\(\frac{1}{2}\)x, \(\frac{1}{2}\)y)
coordinates for D
(-1, -1)
(-1, 1)
(1, 1)
(1, -1)
Identify a sequence of two transformations that will transform figure A into the given figure.
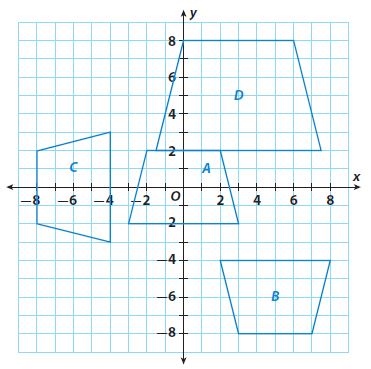
Question 2.
figure B
Type below:
_____________
Answer:
(x, y) -> (x, -y)
(x, y) -> (x +5, y-6)
Question 3.
figure C
Type below:
_____________
Answer:
(x, y) -> (x, y+6)
rotate 90º counterclockwise
Question 4.
figure D
Type below:
_____________
Answer:
(x, y) -> (1.5x, 1.5y)
(x, y) -> (x+3, y+5)
ESSENTIAL QUESTION CHECK-IN
Question 5.
If two figures are similar but not congruent, what do you know about the sequence of transformations used to create one from the other?
Type below:
_____________
Answer:
At least one transformation must be a dilation with a scale factor other than 1
10.3 Independent Practice – Similar Figures – Page No. 331
Question 6.
A designer creates a drawing of a triangular sign on centimeter grid paper for a new business. The drawing has sides measuring 6 cm, 8 cm, and 10 cm, and angles measuring 37°, 53°, and 90°. To create the actual sign shown, the drawing must be dilated using a scale factor of 40.

a. Find the lengths of the sides of the actual sign.
Type below:
_____________
Answer:
240 cm, 320 cm, and 400 cm
Explanation:
6cm × 40 = 240cm
8cm × 40 = 320cm
10cm × 40 = 400cm
The lengths are 240 cm, 320 cm, and 400 cm
Question 6.
b. Find the angle measures of the actual sign.
Type below:
_____________
Answer:
The angle measures are the same
37º, 53º, and 90º
Question 6.
c. The drawing has the hypotenuse on the bottom. The business owner would like it on the top. Describe two transformations that will do this.
Type below:
_____________
Answer:
Reflect the drawing over the x-axis
Rotate the drawing 180º around the origin.
Question 6.
d. The shorter leg of the drawing is currently on the left. The business owner wants it to remain on the left after the hypotenuse goes to the top. Which transformation in part c will accomplish this?
Type below:
_____________
Answer:
Reflecting over the x-axis
In Exercises 7–10, the transformation of a figure into its image is described. Describe the transformations that will transform the image back into the original figure. Then write them algebraically.
Question 7.
The figure is reflected across the x-axis and dilated by a scale factor of 3.
Type below:
_____________
Answer:
Dilate the image by a scale factor of 1/3 and reflect it back across the x-axis.
(x, y) -> (1/3x, 1/3y)
Question 8.
The figure is dilated by a scale factor of 0.5 and translated 6 units left and 3 units up.
Type below:
_____________
Answer:
Translate the image 3 units down and 6 units right and dilate it by a factor of 2
(x, y) -> (x+6, y-3)
(x, y) -> (2x, 2y)
Question 9.
The figure is dilated by a scale factor of 5 and rotated 90° clockwise.
Type below:
_____________
Answer:
Rotate the image 90 counterclockwise and dilate it by a factor of 1/5.
(x, y) -> (-y, x)
(x, y) -> (1/5x, 1/5y)
Similar Figures – Page No. 332
Question 10.
The figure is reflected across the y-axis and dilated by a scale factor of 4.
Type below:
_____________
Answer:
Dilate the image by a factor of 1/4 and reflect it back across the y-axis.
(x, y) -> (1/4x, 1/4y)
(x, y) -> (-x, y)
FOCUS ON HIGHER ORDER THINKING
Question 11.
Draw Conclusions A figure undergoes a sequence of transformations that include dilations. The figure and its final image are congruent. Explain how this can happen.
Type below:
_____________
Answer:
There must be an even number of dilations and for each dilation applied to the figure, a dilation that has the opposite effect must be applied as well.
Question 12.
Multistep As with geometric figures, graphs can be transformed through translations, reflections, rotations, and dilations. Describe how the graph of y = x shown at the right is changed through each of the following transformations.
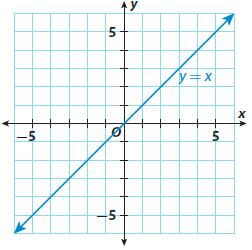
a. a dilation by a scale factor of 4
Type below:
_____________
Answer:
original coordinates
(0, -6)
(0, -4)
(4, 0)
(0, 4)
(-4, 4)
(-4, 2)
(-2, 0)
(-4, -2)
Question 12.
b. a translation down 3 units
Type below:
_____________
Answer:
coordinates for A
(0, -4)
(0, -3)
(2, -1)
(0, 1)
(-2, 1)
(-2, 0)
(-1, -1)
(-2, -2)
Question 12.
c. a reflection across the y-axis
Type below:
_____________
Answer:
coordinates for B
(-4, 3)
(-4, 2)
(-2, 0)
(-4, -2)
(-6, -2)
(-6, -1)
(-5, 0)
(-6, 1)
Question 13.
Justify Reasoning The graph of the line y = x is dilated by a scale factor of 3 and then translated up 5 units. Is this the same as translating the graph up 5 units and then dilating by a scale factor of 3? Explain.
Type below:
_____________
Answer:
No; the dilation is not the same reversed
Explanation:
The position of the sketch from 12A will be 1/2 unit above the sketch obtained when the translation occurs first
Ready to Go On? – Model Quiz – Page No. 333
10.1 Properties of Dilations
Determine whether one figure is a dilation of the other. Justify your answer.
Question 1.
Triangle XYZ has angles measuring 54° and 29°. Triangle X′Y′Z′ has angles measuring 29° and 92°.
_____________
Answer:
No; one figure is not a dilation of the other
Explanation:
The triangles have only one pair of congruent angles
Question 2.
Quadrilateral DEFG has sides measuring 16 m, 28 m, 24 m, and 20 m. Quadrilateral D′E′F′G′ has sides measuring 20 m, 35 m, 30 m, and 25 m.
_____________
Answer:
Yes; Quadrilateral D’E’F’G’ is a dilation of quadrilateral DEFG
Explanation:
each side of the second figure is 1.25 times the corresponding side of the original figure.
10.2 Algebraic Representations of Dilations
Dilate each figure with the origin as the center of dilation.
Question 3.
(x, y) → (0.8x, 0.8y)
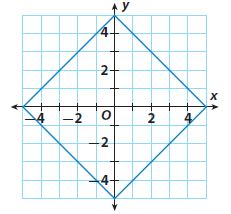
Type below:
_____________
Answer:
Coordinates after dilation
(0, -4)
(4, 0)
(0, 4)
(-4, 0)
Question 4.
(x, y) → (2.5x, 2.5y)
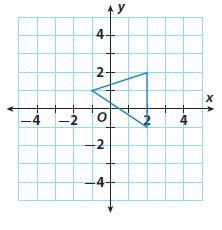
Type below:
_____________
Answer:
Coordinates after dilation
(-2.5, 2.5)
(5, 5)
(5, -3)
10.3 Similar Figures
Question 5.
Describe what happens to a figure when the given sequence of transformations is applied to it: (x, y) → (-x, y); (x, y) → (0.5x, 0.5y); (x, y) → (x – 2, y + 2)
Type below:
_____________
Answer:
After the sequencing of transformations, reflection over the y-axis.
dilation with a scale factor of 0.5
translation 2 units left and 2 units up
ESSENTIAL QUESTION
Question 6.
How can you use dilations to solve real-world problems?
Type below:
_____________
Answer:
You can use dilations when drawing or designing
Selected Response – Mixed Review – Page No. 334
Question 1.
A rectangle has vertices (6, 4), (2, 4), (6, –2), and (2, –2). What are the coordinates of the vertices of the image after a dilation with the origin as its center and a scale factor of 1.5?
Options:
a. (9, 6), (3, 6), (9, –3), (3, –3)
b. (3, 2), (1, 2), (3, –1), (1, –1)
c. (12, 8), (4, 8), (12, –4), (4, –4)
d. (15, 10), (5, 10), (15, –5), (5, –5)
Answer:
a. (9, 6), (3, 6), (9, –3), (3, –3)
Explanation:
(9 -3)/(6 -2) = 6/4 = 1.5
Question 2.
Which represents the dilation shown where the black figure is the preimage?
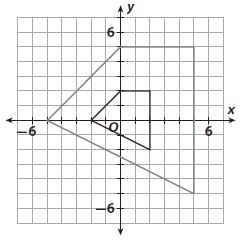
Options:
a. (x, y) -> (1.5x, 1.5y)
b. (x, y) -> (2.5x, 2.5y)
c. (x, y) -> (3x, 3y)
d. (x, y) -> (6x, 6y)
Answer:
b. (x, y) -> (2.5x, 2.5y)
Explanation:
5/2 = 2.5
10/4 = 2.5
(x, y) -> (2.5x, 2.5y)
Question 3.
Identify the sequence of transformations that will reflect a figure over the x-axis and then dilate it by a scale factor of 3.
Options:
a. (x, y) -> (-x, y); (x, y) -> (3x, 3y)
b. (x, y) -> (-x, y); (x, y) -> (x, 3y)
c. (x, y) -> (x, -y); (x, y) -> (3x, y)
d. (x, y) -> (x, -y); (x, y) -> (3x, 3y)
Answer:
d. (x, y) -> (x, -y); (x, y) -> (3x, 3y)
Explanation:
Reflection over x-axis (x, y) -> (x, -y)
dilation by scale factor of 3 (x, y) -> (3x, 3y)
(x, y) -> (x, -y); (x, y) -> (3x, 3y)
Question 4.
Solve −a + 7 = 2a − 8.
Options:
a. a = -3
b. a = −\(\frac{1}{3}\)
c. a = 5
d. a = 15
Answer:
c. a = 5
Explanation:
-a + 7 = 2a – 8
2a + a = 8 + 7
3a = 15
a = 15/3
a = 5
Question 5.
Which equation does not represent a line with an x-intercept of 3?
Options:
a. y = −2x + 6
b. y = −\(\frac{1}{3}\)x + 1
c. y = \(\frac{2}{3}\)x − 2
d. y = 3x − 1
Answer:
d. y = 3x − 1
Explanation:
y = -2x + 6
0 = -2x + 6
2x = 6
x = 3
y = -1/3 . x + 1
0 = -1/3 . x + 1
1/3x = 1
x = 3
y = 2/3 . x – 2
0 = 2/3 . x – 2
2/3x = 2
x = 2 . 3/2
x = 3
y = 3x – 1
0 = 3x – 1
3x = 1
x = 1/3
Mini-Task
Question 6.
The square is dilated under the dilation (x, y) → (0.25x, 0.25y).
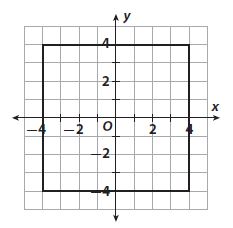
a. Graph the image. What are the coordinates?
Type below:
_____________
Answer:
After dilation:
(-1, 1)
(1, 1)
(1, -1)
(-1, -1)
Question 6.
b. What is the length of a side of the image?
______ units
Answer:
2 units
Explanation:
The length is 2 units
Question 6.
c. What are the perimeter and area of the preimage?
Perimeter = ________ units
Area = ________ square units
Answer:
Perimeter = 32 units
Area = 64 square units
Explanation:
Perimeter = 2l + 2w = 2(8) + 2(8) = 32
area = l.w = 8 .8 = 64
Question 6.
d. What are the perimeter and area of the image?
Perimeter = ________ units
Area = ________ square units
Answer:
Perimeter = 8 units
Area = 4 square units
Explanation:
Perimeter = 2l + 2w = 2(2) + 2(2) = 8
area = l.w = 2 . 2 = 4
Conclusion:
The Go Math Grade 8 Solution Key Chapter 10 Transformations and Similarity help the students to enhance their math skills. All the explanations are given by the best maths experts. So, to learn maths in the best way, you must refer to HMH Go Math Grade 8 Solution Key. Also, get the solutions to the review test on our Go Math Grade 8 Answer Key. Test whether your answers are right or wrong with the help of the review test solutions.
