Students of 7th grade can get a detailed explanation for all the problems in Go Math Answer Key Chapter 8 Modeling Geometric Figures. Redefine yourself by practicing problems from Go Math Grade 7 Answer Key Chapter 8 Modeling Geometric Figures. We have given the pdf to Download HMH Go Math Answer Key of Grade 7 Chapter 8 Modeling Geometric Figures. So, refer to Go Math 7th Grade Answer Key Chapter 8 Modeling Geometric Figures to secure the highest score in exams.
Go Math Grade 7 Answer Key Chapter 8 Modeling Geometric Figures
Get access to Download HMH Go Math Grade 7 Key Chapter 8 Modeling Geometric Figures here. Start preparing for your exams by using the Go Math Grade 7 Answer Key Chapter 8 Modeling Geometric Figures pdf. In this article, you can check the answers to review questions in addition to the exercise and homework questions. So, make use of the below links and learn the problems according to the topics.
Chapter 8 – Modeling Geometric Figures – Lesson: 1
Chapter 8 – Modeling Geometric Figures – Lesson: 2
Chapter 8 – Modeling Geometric Figures – Lesson: 3
Chapter 8 – Modeling Geometric Figures – Lesson: 4
Chapter 8 – Modeling Geometric Figures
Guided Practice – Page No. 240
Question 1.
The scale of a room in a blueprint is 3 in : 5 ft. A wall in the same blueprint is 18 in. Complete the table.

a. How long is the actual wall?
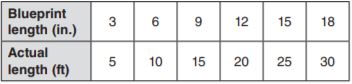
______ feet
Answer: 30 feet
Explanation:
We complete the table using the direct proportionality
3 in : 5 ft.
A wall in the same blueprint is 18 in. is 30 feet.
Question 1.
b. A window in the room has an actual width of 2.5 feet. Find the width of the window in the blueprint.
______ inches
Answer: 1.5 inches
Explanation:
We determine the number of inches corresponding to 1 foot on the actual window
3 in /5 in.
Multiply and divide by 5
(3 in ÷ 5)/(5 ft ÷ 5) = 0.6/1 ft
Thus 1 foot corresponds to 0.6 inches, so the width of the window in the table is
2.5 × 0.6 = 1.5 inches
Question 2.
The scale in the drawing is 2 in. : 4 ft. What are the length and width of the actual room? Find the area of the actual room.

Width: _________ feet
Length: _________ feet
Area: _________ sq ft
Answer:
Width: 28 feet
Length: 14 feet
Area: 392 sq ft
Explanation:
We determine the number of feet corresponding to 1 inch in the drawing
2 in/4 in = (2 in. ÷ 2)/(4 in ÷ 2) = 1/2
Thus 1 inch corresponds to 2 feet on the actual dimensions of the room.
We determine the actual length of the room, labeled 14 inches in the drawing.
14 × 2 = 28 feet
We determine the actual width of the room, labeled 7 inches in the drawing.
7 × = 14 feet
We compute the area of the actual room:
28 × 14 = 392 square feet.
Question 3.
The scale in the drawing is 2 cm: 5 m. What are the length and width of the actual room? Find the area of the actual room.
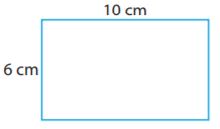
Width: _________ m
Length: _________ m
Area: _________ sq meters
Answer:
Width: 25 m
Length: 15 m
Area: 375 sq meters
Explanation:
We determine the number of meters corresponding to 1 centimeter in the drawing:
2 cm/5 cm = (2 cm ÷ 2)/(5 cm ÷ 2) = 1 cm/ 2.5 m
We determine the actual length of the room, labeled 10 cm in the drawing:
10 × 2.5 = 25 m
We determine the actual width of the room, labeled 6 cm in the drawing:
6 × 2.5 = 15 m
We compute the area of the room:
25 × 15 = 375 square feet.
Question 4.
A scale drawing of a cafeteria is drawn on centimeter grid paper as shown. The scale is 1 cm: 4 m.
a. Redraw the rectangle on centimeter grid paper using a scale of 1 cm:6 m.
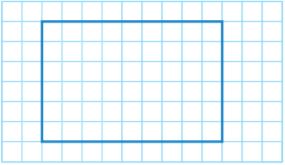
Type below:
_____________
Answer:
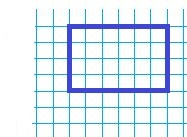
Question 4.
b. What is the actual length and width of the cafeteria using the original scale? What are the actual dimensions of the cafeteria using the new scale?
Length: _________ m
Width: _________ m
Answer:
In the original scale, the dimensions on the drawing are
l1 = 9 cm
w1 = 6 cm
We determine the actual length using the original scale:
9 × 4 = 36
We determine the actual width using the original scale:
6 × 4 = 24
In the second scale, the dimensions on the drawing are
l2 = 6 cm
w1 = 4 cm
We determine the actual length using the original scale:
6 × 6 = 36
We determine the actual width using the original scale:
4 × 6 = 24
Thus the length is 36m
Width is 24 m
Essential Question Check-In
Question 5.
If you have an accurate, complete scale drawing and the scale, which measurements of the object of the drawing can you find?
Type below:
_____________
Answer:
If we have an accurate, complete scale drawing and scale, we can determine all measurements of the object because they are all proportional with the dimensions on the drawing the ratio being the scale.
Independent Practice – Page No. 241
Question 6.
Art
Marie has a small copy of Rene Magritte’s famous painting, The Schoolmaster. Her copy has dimensions 2 inches by 1.5 inches. The scale of the copy is 1 in.:40 cm.
a. Find the dimensions of the original painting.
Length: _________ cm
Width: _________ cm
Answer:
Length: 80 cm
Width: 60 cm
Explanation:
We are given the data
Scale: 1 in:40 cm
Copy l1 = 2 in.
w1 = 1.5 inches
We determine the length l of the original painting
l = 2 × 40 = 80cm
We determine the width w of the original painting
w = 1.5 × 40 = 60 cm
Question 6.
b. Find the area of the original painting.
_____________ sq cm
Answer: 4800 square cm
Explanation:
We determine the width w of the original painting
A = l.w
A = 80 × 60 = 4,800 square cm
Question 6.
c. Since 1 inch is 2.54 centimeters, find the dimensions of the original painting in inches.
Length: _________ inches
Width: _________ inches
Answer:
We determine the length l of the original painting in inches:
1 in. = 2.54 cm
l = 80/2.54 cm ≈ 31.5 inches
We determine the width w of the original painting in inches:
w = 60/2.54 ≈ 23.6 inches
Question 6.
d. Find the area of the original painting in square inches
_____________ sq inches
Answer: 743.4 square inches
Explanation:
We find the area of the original painting in the square inches:
l × w = 31.5 × 23.6 = 743.4 square inches
Thus the area of the original painting is 743.4 square inches.
Question 7.
A game room has a floor that is 120 feet by 75 feet. A scale drawing of the floor on grid paper uses a scale of 1 unit:5 feet. What are the dimensions of the scale drawing?
Length: _________ units
Width: _________ units
Answer:
Length: 24 units
Width: 15 units
Explanation:
We are given the data:
Scale: 1 unit: 5 feet
Actual dimensions: l = 120 feet, w = 75 feet
We determine the number of units on the drawing corresponding to 1 foot from the actual dimensions.
1 unit/ 5 feet
(1 unit ÷ 5)/(5 feet ÷ 5) = 0.2 units/1 feet
We determine the length of the scale drawing:
120 × 0.2 = 24 units
We determine the width of the scale drawing:
75 × 0.2 = 15 units
Question 8.
Multiple Representations
The length of a table is 6 feet. On a scale drawing, the length is 2 inches. Write three possible scales for the drawing.
Type below:
_____________
Answer:
l = 6 feet
l1 = 2 inches
l = the actual length
l1 = the length on a scale drawing
2 inches:6 ft
1 in:3 ft
2/6×12 = 2/72 = 1/36
1 cm: 36 cm
Question 9.
Analyze Relationships
A scale for a scale drawing is 10 cm:1 mm. Which is larger, the actual object or the scale drawing? Explain.
_____________
Answer:
We are given the scale
10 cm: 1 mm
100 mm: 1 m
This means that the correspondent in actual dimension for 100 mm of drawing is 1mm, so to a greater on the drawing there is a smaller actual distance, therefore the scale drawing is larger.
Question 10.
Architecture
The scale model of a building is 5.4 feet tall.
a. If the original building is 810 meters tall, what was the scale used to make the model?
______ ft. : ______ m
Answer: 1 foot: 150 m
Explanation:
Let’s note:
h1 = the height on the scale model
h = the actual height
We are given the data
h1 = 5.4 feet
h = 810 meters
We determine the scale for the model
h1/h = 5.4 feet/810 m = (5.4 feet ÷ 5.4)/(810 ÷ 5.4)
1 foot/150 m
1 foot: 150 m
Question 10.
b. If the model is made out of tiny bricks each measuring 0.4 inch in height, how many bricks tall is the model?
___________ bricks
Answer: 14 bricks
Explanation:
We determine the scale for the model:
h1/0.4 = 5.4/0.4 = 13.5
The number of bricks: 14
Page No. 242
Question 11.
You have been asked to build a scale model of your school out of toothpicks. Imagine your school is 30 feet tall. Your scale is 1 ft:1.26 cm.
a. If a toothpick is 6.3 cm tall, how many toothpicks tall will your model be?
______ toothpicks
Answer: 6
Explanation:
Given that,
h = 30 feet
1 ft: 1.26 cm
h1 = the height on the scale model
h = the actual height
We determine the height h1 of the model:
h1 = 30 × 1.26 = 37.8 cm
h1/6.3 = 37.8/6.3 = 6
Thus the number of toothpicks = 6
Question 11.
b. Your mother is out of toothpicks, and suggests you use cotton swabs instead. You measure them, and they are 7.6 cm tall. How many cotton swabs tall will your model be?
______ cotton swabs
Answer: 5
Explanation:
We find the number of cotton wabs
h1/7.6 = 37.8/7.6 ≈ 5
Thus the number of cotton wabs = 5
H.O.T.
Focus on Higher Order Thinking
Question 12.
Draw Conclusions
The area of a square floor on a scale drawing is 100 square centimeters, and the scale of the drawing is 1 cm : 2 ft. What is the area of the actual floor? What is the ratio of the area in the drawing to the actual area?
Area = ______ sq. ft.
Answer: 400 sq. ft
Explanation:
A1 = the area of the drawing
A = the area of the actual floor
We are given the data:
A1 = 100 cm²
1 cm: 2 ft
1 cm corresponds to 2 ft
1 cm × 1 cm corresponds to 2 ft × 2 ft
1 cm² corresponds to 4 ft²
A = 100. 4 = 400 ft²
We determine the ratio of the area in the drawing to the actual area:
1 ft = 0.3048 m = 30.48 cm
A1/A = 100/400 × 30.48² ≈ 0.0003
Question 13.
Multiple Representations
Describe how to redraw a scale drawing with a new scale.
Type below:
_____________
Answer:
In order to redraw a scale drawing with a new scale we perform 2 steps:
1. We find how many times the new scale us bigger or smaller than the old one.
2. We multiply this scale factor by the dimensions of the old scale drawing to get a new drawing.
Question 14.
Represent Real-World Problems
Describe how several jobs or professions might use scale drawings at work.
Type below:
_____________
Answer:
Scale drawings are extremely useful in jobs which need to represent bigger areas on smaller devices like
1. Architecture/ constructions
2. medicine
3. agriculture
4. tourism
5. transportation
Guided Practice – Page No. 245
Tell whether each figure creates the conditions to form a unique triangle, more than one triangle, or no triangle.
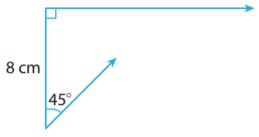
Question 1.
Type below:
_____________
Answer: A unique triangle
Explanation:
We are given two angles and the included side, thus there is a unique triangle as the sides leaving from B and A intersect in a unique point.
Question 2.
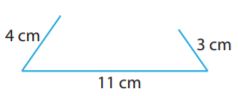
Type below:
_____________
Answer: No triangle
Explanation:
We are given the three sides of the triangle. We check if the sum of any two sides is greater than the other.
4 + 11 = 15 > 3
11 + 3 = 14 > 4
3 + 4 = 7 is not greater than 11.
Because one inequality is not verified, the triangle doesn’t exist.
Question 3.
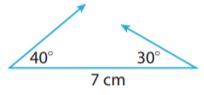
Type below:
_____________
Answer: A unique triangle
Explanation:
We are given two angles and the included side, thus there is a unique triangle as the sides leaving from B and A intersect in a unique point.
Question 4.
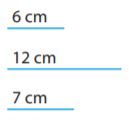
Type below:
_____________
Answer: A unique triangle
Explanation:
We are given the three sides of the triangle. We check if the sum of any two sides is greater than the other.
6 + 12 = 18 > 7
12 + 7 = 19 > 6
6 + 7 = 13 > 12
Since all inequalities are verified, there is a unique triangle.
Essential Question Check-In
Question 5.
Describe lengths of three segments that could not be used to form a triangle.
Type below:
_____________
Answer:
Find the lengths of three segments not to be the sides of a triangle, at least one sum of two sides should be smaller than the other side.
Let a, b, c be the lengths of the three segments.
a + b not > a + b + k = c
Independent Practice
Question 6.
On a separate piece of paper, try to draw a triangle with side lengths of 3 centimeters and 6 centimeters, and an included angle of 120°. Determine whether the given segments and angle produce a unique triangle, more than one triangle, or no triangle.
Type below:
_____________
Answer: A unique triangle
Explanation:
∠A = 120°
AB = 6
AC = 3
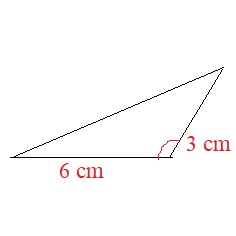
We draw the segment AB, the angle A and the segment AC, then we join B and C. The result is an unique triangle.
Question 7.
A landscape architect submitted a design for a triangle-shaped flower garden with side lengths of 21 feet, 37 feet, and 15 feet to a customer. Explain why the architect was not hired to create the flower garden.
Type below:
_____________
Answer:
We are given the sides of a triangle
21 + 37 = 58 > 15
37 + 15 = 52 > 21
15 + 21 = 36 not > 37
We checked the three triangles inequalities
Thus the triangle does not exist, that is the reason why the architect was not hired to create the flower garden.
Page No. 246
Question 8.
Make a Conjecture
The angles in an actual triangle-shaped traffic sign all have measures of 60°. The angles in a scale drawing of the sign all have measures of 60°. Explain how you can use this information to decide whether three given angle measures can be used to form a unique triangle or more than one triangle.

Type below:
_____________
Answer: Three given angle measures whose sum is 180° can be used to form an infinity of triangles, having the property that their corresponding sides are proportional.
H.O.T.
Focus on Higher Order Thinking
Question 9.
Communicate Mathematical Ideas
The figure on the left shows a line segment 2 inches long forming a 45° angle with a dashed line whose length is not given. The figure on the right shows a compass set at a width of 1 \(\frac{1}{2}\) inches with its point on the top end of the 2-inch segment. An arc is drawn intersecting the dashed line twice.
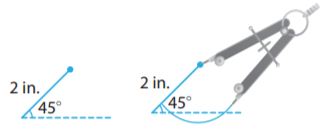
Explain how you can use this figure to decide whether two sides and an angle not included between them can be used to form a unique triangle, more than one triangle, or no triangle.
Type below:
_____________
Answer:
A trinagle does not exist because one side is shorter than the other two sides. The circle intersects the dashed line only once so that one angles is 45°, so there is only one solution. The circle with the center in B intersects the dashed line twice, thus there are two triangles formed.
Question 10.
Critical Thinking
Two sides of an isosceles triangle have lengths of 6 inches and 15 inches, respectively. Find the length of the third side. Explain your reasoning.
_______ inches
Answer: 15 inches
Explanation:
We are given the two sides of an isosceles triangle
a = 6
b = 15
There are two possibilities the third side is equal to a or b. Lets study both of them
Case 1: a = c = 6, b = 15
a + c = 6 + 6 = 12 not greater than 15 = b
We check the three triangle’s inequalities
a + b = 6 + 15 = 21 > 15 = c
a + c = 6 + 15 = 21 > 15 = b
b + c = 15 + 15 = 30 > 6 = a
Case 2: a = 6, b = c = 15
Thus the third side of the triangle is 15.
Guided Practice – Page No. 249
Describe each cross section.
Question 1.
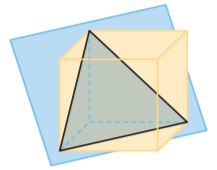
Type below:
_____________
Answer: Triangle/Quadrilateral triangle
The given cross-section in a cube is a triangle/equilateral triangle.
Question 2.
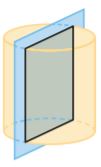
Type below:
_____________
Answer: Rectangle
The given cross-section in a cylinder is a rectangle.
Question 3.
Type below:
_____________
Answer: Triangle
Explanation:
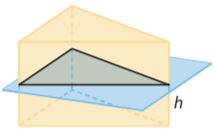
The given cross-section in the prism is the triangle.
Question 4.
Type below:
_____________
Answer: Rainbow shaped curve
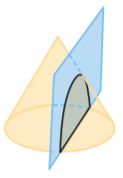
The given cross-section in the cone is a rainbow-shaped curve.
Essential Question Check-In
Question 5.
What is the first step in describing what figure results when a given plane intersects a given three-dimensional figure?
Type below:
_____________
Answer:
The first step in describing what figure results when a given plane intersects a given three-dimensional figure is to establish the number of sides the cross-section has.
Independent Practice
Question 6.
Describe different ways in which a plane might intersect the cylinder and the cross section that results.
Type below:
_____________
Answer:
The cross-section can be:
1. a circle
2. an ellipse
3. a rectangle
Page No. 250
Question 7.
Make a Conjecture
What cross sections might you see when a plane intersects a cone that you would not see when a plane intersects a pyramid or a prism?
Type below:
_____________
Answer:
The cross-section can be:
1. a circle
2. an ellipse
3. a parabola
4. a hyperbola
5. a triangle
H.O.T.
Focus on Higher Order Thinking
Question 8.
Critical Thinking
The two figures on the left below show that you can form a cross section of a cube that is a pentagon. Think of a plane cutting the cube at an angle in such a way as to slice through five of the cube’s six faces. Draw dotted lines on the third cube to show how to form a cross section that is a hexagon.

Type below:
_____________
Answer:
We draw a plane cutting the cube so that the cross-section is a hexagon: for this, we take the middle of 6 adjacent sides:
Question 9.
Analyze Relationships
A sphere has a radius of 12 inches. A horizontal plane passes through the center of the sphere.
a. Describe the cross section formed by the plane and the sphere
Type below:
_____________
Answer: Circle
Explanation:
We are given a sphere and a cross-section passing through the center of the sphere:
The cross section passing through the center of the sphere is a circle having the radius equal to the sphere’s radius.
Question 9.
b. Describe the cross sections formed as the plane intersects the interior of the sphere but moves away from the center.
Type below:
_____________
Answer: The cross sections formed as a plane intersects the interior of the sphere outside the center are circles.
Question 10.
Communicate Mathematical Ideas
A right rectangular prism is intersected by a horizontal plane and a vertical plane. The cross section formed by the horizontal plane and the prism is a rectangle with dimensions 8 in. and 12 in. The cross section formed by the vertical plane and the prism is a rectangle with dimensions 5 in. and 8 in. Describe the faces of the prism, including their dimensions. Then find its volume.
Type below:
_____________
Answer: 480 cube inches
Explanation:
The horizontal cross section has the dimensions 8×12, while the vertical 5×8.
The prism has the dimensions:
5 inches, 8 inches, 12 inches
We find the volume of the prism:
5 × 8 × 12 = 480 cube inches
Question 11.
Represent Real-World Problems
Describe a real-world situation that could be represented by planes slicing a three-dimensional figure to form cross sections.
Type below:
_____________
Answer:
Examples of real-world situations that can be represented by planes slicing three-dimensional figures to form cross-sections:
– electrical wires
– water/gas pipes
– house design
– geology
– seismology
Guided Practice – Page No. 256
For 1–2, use the figure.
Question 1.
Vocabulary
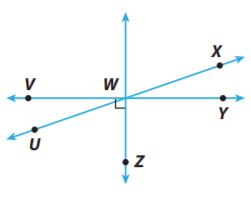
The sum of the measures of ∠UWV and ∠UWZ is 90°, so ∠UWV and ∠UWZ are _____ angles.
Type below:
_____________
Answer: Complementary angles
Explanation:
The sum of ∠UWV and ∠UWZ is 90°, so ∠UWV and ∠UWZ are complementary angles.
Question 2.
Vocabulary
∠UWV and ∠VWX share a vertex and one side. They do not overlap, so ∠UWV and ∠VWX are _____ angles.
Type below:
_____________
Answer: Adjacent angles
Explanation:
∠UWV and ∠VWX share a vertex and one side. They do not overlap, so ∠UWV and ∠VWX are adjacent angles.
For 3–4, use the figure.
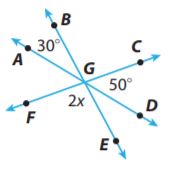
Question 3.
∠AGB and ∠DGE are _____ angles, so m∠DGE = _____.
Type below:
_____________
Answer: ∠AGB and ∠DGE are vertical angles, so m∠DGE = m∠AGB = 30°
Question 4.
Find the measure of ∠EGF.
_______ °
Answer: 100°
Explanation:
m∠CGD + m∠DGE + m∠EGF = 180°
50° + m∠AGB + m∠EGF = 180°
50° + 30° + 2x = 180°
2x = 180° – 80°
2x = 100°
mm∠EGF = 2x = 100°
Question 5.
Find the value of x and the measure of ∠MNQ.
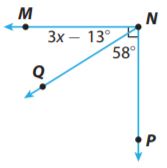
x = _______ °
mMNQ = _______ °
Answer:
∠MNQ + ∠QNP = 90°
3x – 13° + 58° = 90°
3x = 90° + 13° – 58°
3x = 45°
x = 15°
m∠MNQ = 3x – 13°
= 3×15° – 13°
= 45° – 13°
= 32°
Essential Question Check-In
Question 6.
Suppose that you know that ∠T and ∠S are supplementary and that m∠T = 3(m∠S). How can you find m∠T?
Type below:
_____________
Answer:
m∠T + m∠S = 180°
m∠T = 3(m∠S)
m∠S = m∠T/3
Form the second equation we write m∠S in terms of m∠T
m∠T + m∠T/3 = 3 × 180°
3m∠T + m∠T = 3 × 180°
4m∠T = 540°
m∠T = 540°/4
m∠T = 135°
Independent Practice – Page No. 257
For 7–11, use the figure.
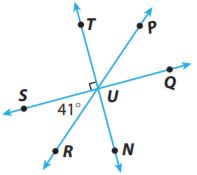
Question 7.
Name a pair of adjacent angles. Explain why they are adjacent.
Type below:
_____________
Answer:
The pair of adjacent angles are:
∠SUR and ∠RUN (common vertex U and one common side – UR – without overlapping)
∠NUQ and ∠QUP (common vertex U and one common side – UQ – without overlapping)
∠PUT and ∠TUS (common vertex U and one common side – UT – without overlapping)
Question 8.
Name a pair of acute vertical angles.
Type below:
_____________
Answer:
By seeing the above figure we can say that ∠SUR and ∠PUQ are the vertical angles.
Question 9.
Name a pair of supplementary angles.
Type below:
_____________
Answer:
The above figure shows that ∠SUR and ∠RUQ are supplementary angles.
Question 10.
Justify Reasoning
Find m∠QUR. Justify your answer.
_______ °
Answer:
We have to find m∠QUR.
∠SUR and ∠QURare supplementary angles.
m∠SUR + m∠QUR = 180°
m∠QUR + 41° = 180°
m∠QUR = 180° – 41°
m∠QUR = 139°
Question 11.
Draw Conclusions
Which is greater, m∠TUR or m∠RUQ? Explain.
Type below:
_____________
Answer:
m∠QUR = 139°
m∠TUR = m∠TUS + m∠SUR
90° + 41° = 131°
We find m∠TUR
139° > 131°
m∠QUR > m∠TUR
For 12–13, use the figure. A bike path crosses a road as shown. Solve for each indicated angle measure or variable.
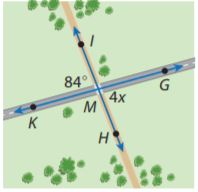
Question 12.
x = ?
_______ °
Answer: x = 21°
Explanation:
∠KMI and ∠HMG are vertical, thus congruent.
We determine x:
84° = 4x
4x = 84°
x = 84°/4
x = 21°
Question 13.
m∠KMH = ?
_______ °
Answer: 96°
Explanation:
∠KMI and ∠KMH are supplementary.
We determine m∠KMH:
m∠KMH + m∠KMI = 180°
m∠KMH + 84° = 180°
m∠KMH = 180° – 84°
m∠KMH = 96°
For 14–16, use the figure. Solve for each indicated angle measure.
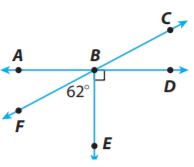
Question 14.
m∠CBE = ?
_______ °
Answer: 118°
Explanation:
We determine m∠CBE:
m∠CBE + m∠EBF = 180°
m∠CBE + 62°= 180°
m∠CBE = 180° – 62°
m∠CBE = 118°
Question 15.
m∠ABF = ?
_______ °
Answer: 28°
Explanation:
We determine m∠ABF
m∠ABF + m∠EBF = 90°
m∠ABF + 62° = 90°
m∠ABF = 90° – 62°
m∠ABF = 28°
Question 16.
m∠CBA = ?
_______ °
Answer: 152°
Explanation:
We determine m∠CBA
m∠CBA = m∠DBF = m∠DBE + m∠EBF
90° + 62° = 152°
m∠CBA = 152°
Question 17.
The measure of ∠A is 4° greater than the measure of ∠B. The two angles are complementary. Find the measure of each angle.
mA = __________ °
mB = __________ °
Answer:
mA = 47°
mB = 43°
Explanation:
We are given the data:
m∠A = m∠B + 4°
m∠A + m∠B = 90°
m∠B + 4° + m∠B = 90°
2m∠B = 90° – 4°
2m∠B = 86°
m∠B = 86°/2
m∠B = 43°
m∠A = m∠B + 4°
m∠A = 43° + 4°
m∠A = 47°
Question 18.
The measure of ∠D is 5 times the measure of ∠E. The two angles are supplementary. Find the measure of each angle.
mD = __________ °
mE = __________ °
Answer:
mD = 150°
mE = 30°
Explanation:
We are given the data
m∠D = 5(m∠E)
m∠D + m∠E = 180°
5(m∠E) + m∠E = 180°
6 m∠E = 180°
m∠E = 180°/6
m∠E = 30°
m∠D = 5(m∠E)
m∠D = 5 × 30°
m∠D = 150°
Page No. 258
Question 19.
Astronomy
Astronomers sometimes use angle measures divided into degrees, minutes, and seconds. One degree is equal to 60 minutes, and one minute is equal to 60 seconds. Suppose that ∠J and ∠K are complementary, and that the measure of ∠J is 48 degrees, 26 minutes, 8 seconds. What is the measure of ∠K?
_______ ° _______ ‘ _______ ”
Answer: 41° 33 ‘ 52″
Explanation:
We are given the data
m∠J + m∠K = 90°
m∠J = 48° 26 ‘ 8″
90° – 48° 26 ‘ 8″
89°60’ – 48° 26 ‘ 8″
89°59’60” – 48° 26 ‘ 8″ = 41° 33 ‘ 52″
Thus the measure of ∠K is 41° 33 ‘ 52″
H.O.T.
Focus on Higher Order Thinking
Question 20.
Represent Real-World Problems
The railroad tracks meet the road as shown. The town will allow a parking lot at angle K if the measure of angle K is greater than 38°. Can a parking lot be built at angle K ? Why or why not?
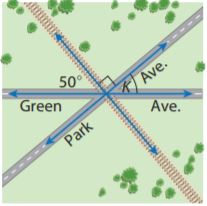
_______
Answer:
m∠K = 180° – 50° – 90° = 40°
Since m∠K = 40°> 38°, a parking lot can be built.
Question 21.
Justify Reasoning
Kendra says that she can draw ∠A and ∠B so that m∠A is 119° and ∠A and ∠B are complementary angles. Do you agree or disagree? Explain your reasoning.
_______
Answer:
We are given the data
m∠A = 119°
m∠A + m∠B = 90°
m∠B = 90° – m∠A
= 90° – 119° = -29°
Since m∠B < 0, Kendra is wrong, she cannnot draw the angles.
Question 22.
Draw Conclusions
If two angles are complementary, each angle is called a complement of the other. If two angles are supplementary, each angle is called a supplement of the other.
a. Suppose m∠A = 77°. What is the measure of a complement of a complement of ∠A? Explain.
_______ °
Answer: 77°
Explanation:
90° – (90° – m∠A) = 90° – (90° – 77°)
90° – 77° = 13°
77°
Question 22.
b. What conclusion can you draw about a complement of a complement of an angle? Explain.
Type below:
_____________
Answer:
The complement of a complement of an angle is the angle itself:
90° – (90° – m∠A)
90° – 90° + m∠A
8.1 Similar Shapes and Scale Drawings – Page No. 259
Question 1.
A house blueprint has a scale of 1 in. : 4 ft. The length and width of each room in the actual house are shown in the table. Complete the table by finding the length and width of each room on the blueprint.
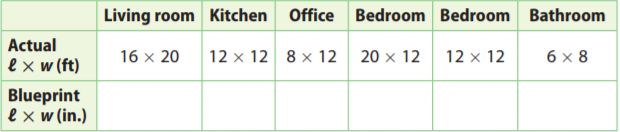
Type below:
_____________
Answer:
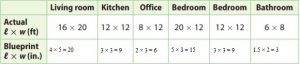
Thus for each 4 ft in actual dimension, there is 1 inch in the blueprint.
8.2 Geometric Drawings
Question 2.
Can a triangle be formed with the side lengths of 8 cm, 4 cm, and 12 cm?
______
Answer:
We are given the side lengths
8 + 12 = 20 > 4
4 + 12 = 16 > 8
8 + 4 not > 12
Since one of the inequalities is not verified, the three given side lengths cannot form a triangle.
Question 3.
A triangle has side lengths of 11 cm and 9 cm. Which could be the value of the third side, 20 cm or 15 cm?
______
Answer: 15 cm
Explanation:
We are given the side lengths
11, 9
11 + 9 = 20 not > 20
We check the triangle’s inequalities if we add the third side of 20 cm
Since one of the inequalities is not verified, the three given side lengths cannot form a triangle.
11, 9, 15
11 + 9 = 20 > 15
11 + 15 = 26 > 9
15 + 9 = 24 > 11
We check the triangle’s inequalities are verified, 15 can be the value of the third side.
8.3 Cross Sections
Question 4.
Name one possible cross section of a sphere.
Type below:
_____________
Answer: Circle
One possible cross section of the sphere is a circle.
Question 5.
Name at least two shapes that are cross sections of a cylinder.
Type below:
_____________
Answer: Three possible cross-sections of a cylinder are a circle, an ellipse, and a rectangle.
Essential Question Check-In
Question 5.
How can you model geometry figures to solve real-world problems?
Type below:
_____________
Answer: You can model geometry for making buildings and sky scrapers, also stores.
8.4 Angle Relationships
Question 6.
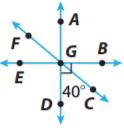
∠BGC and ∠FGE are _____ angles, so m∠FGE = _____
_____ °
Answer: ∠BGC and ∠FGE are vertical angles, so m∠FGE = m∠BGC = 90° – 40° = 50°
Question 7.
Suppose you know that ∠S and ∠Y are complementary, and that m∠S = 2(m∠Y) – 30°. Find m∠Y.
m?Y = _____ °
Answer: 40°
Explanation:
m∠S + m∠Y = 90°
m∠S = 2(m∠Y) – 30°
We replace the expression of m∠S from the second equation into the first we can find m∠Y
2(m∠Y) – 30° + m∠Y = 90°
3m∠Y = 90° + 30°
3m∠Y = 120°
m∠Y = 120°/3
m∠Y = 40°
Selected Response – Page No. 260
Question 1.
Which number can you add to 15 to get a sum of 0?
Options:
a. -10
b. -15
c. 0
d. 15
Answer: -15
Explanation:
The number we add to a number in order to get a sum of zero is its opposite. In or case we should add -15 to 15.
15 + (-15) = 0
Thus the correct answer is option B.
Question 2.
Students are painting the backdrop for the school play. The backdrop is 15 feet wide and 10 feet high. Every 16 inches on the scale drawing represents 5 feet on the backdrop. What is the area of the scale drawing?
Options:
a. 150 in2
b. 6 in2
c. 3096
d. 1536 in2
Answer: 1536 in2
Explanation:
We are given the dimensions l and w of the backdrop and the drawing scale:
l = 15 ft
w = 10 ft
16 in: 5 ft
16 in./5 ft = (16 in. ÷ 5)/(5 ft ÷ 5) = 3.2 in/1 ft
l1 = 15 × 3.2 = 48 inches
w1 = 10 × 32 = 320 inches
l1 × w1 = 48 × 32 = 1536 square inches
Thus the correct answer is option D.
Question 3.
Two sides of a triangle measure 8 cm and 12 cm. Which of the following CANNOT be the measure of the third side?
Options:
a. 4
b. 12
c. 8
d. 16
Answer: 4 cm
Explanation:
We are given two sides of a triangle
a. 4
4 + 8 not > 12
b. 12
12 + 8 > 12
12 + 12 > 8
c. 8
8 + 8 > 12
8 + 12 > 12
d. 16
8 + 12 > 16
8 + 16 > 12
12 + 16 > 8
Thus the only dimension which cannot be the measure of the third side f the triangle is 4 cm.
Thus the correct answer is option A.
Question 4.
A cross section is the intersection of a three-dimensional figure and a _____ .
Options:
a. point
b. plane
c. line
d. set
Answer: Plane
Explanation:
A cross section is the interaction of a three-dimensional figure and a plane.
Thus the correct answer is option B.
For 5–6, use the diagram.
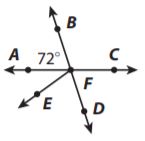
Question 5.
What is the measure of ∠BFC?
Options:
a. 18
b. 108
c. 72
d. 144
Answer: 108°
Explanation:
∠BFC + ∠BFA = 180°
∠BFC + 72° = 180°
∠BFC = 180° – 72°
∠BFC = 108°
The angles ∠BFC and ∠BFA are supplementary. We determine ∠BFC.
Thus the correct answer is option B.
Question 6.
Which describes the relationship between ∠BFA and ∠CFD?
Options:
a. adjacent angles
b. complementary angles
c. supplementary angles
d. vertical angles
Answer: vertical angles
Explanation:
The angles ∠BFA and ∠CFD are vertical angles because they are opposite angles formed at the intersection of two lines.
Thus the correct answer is option D.
Question 7.
All clothing is being marked down 15%. Which expression represents the new retail price?
Options:
a. 0.85x
b. 1.15x
c. 1.85x
d. 0.15x
Answer: 0.85x
Explanation:
x = initial price
Since the price went down by 15%, the new price will be diminished by 15/100 x
x – 0.15x = 0.85x
Thus the correct answer is option A.
Mini-Tasks
Question 8.
Ira built a model of the Great Pyramid in Egypt for a school project. The Great Pyramid has a square base with sides of length 756 feet. The height of the Great Pyramid is 481 feet. Ira made his model pyramid using a scale of 1 inch : 20 feet.
a. What is the length of each side of the base of Ira’s pyramid?
_____ in
Answer: 37.8 inches
We compute the number of inches corresponding to 1 feet from the actual dimensions:
1 in./20 ft = (1 in. ÷ 20)/(20 ft ÷ 20) = 0.05 in/1 ft.
There are 0.05 inches for 1 feet.
We determine the length of Ira’s pyramid base:
756 × 0.05 = 37.8 inches
Question 8.
b. What is the area of the base of Ira’s pyramid?
_____ square inches
Answer: 1428.84 square inches
Explanation:
We determine the area of Ira’s pyramid base:
37.8 × 37.8 = 1,428.84 square inches.
Question 8.
c. What is the height of Ira’s pyramid?
_____ in
Answer:
We determine the height of Ira’s pyramid:
481 × 0.05 = 24.05 inches
Question 8.
d. Ira built his model using cross sections that were cut parallel to the base. What shape was each cross section?
Type below:
____________
Answer: The cross sections parallel to the base have the shape of a square.
Final Words:
Hope the solutions provided in Go Math Grade 7 Answer Key Chapter 8 Modeling Geometric Figures is helpful for all the students. Get the answers for all the questions with the simple techniques for all chapters on Go Math Answer 7th grade Key Chapter 8 Modeling Geometric Figures. Stick to our Go Math Answer Key Page to get the latest information about the chapters.
