Access the answers by downloading the 7th Grade HMH Go Math Answer Key Chapter 6 Algebraic Expressions pdf. We have prepared the solutions for all the questions in an easy manner. Thus we advise the students who are willing to score the highest marks to go through the Go Math Grade 7 Answer Key Chapter 6 Algebraic Expressions. The solutions seen in Go Math 7th Grade Solution Key Chapter 6 Algebraic Expressions are prepared by the math experts. So don’t worry about the solutions just go through the topics and start your preparation.
Go Math Grade 7 Answer Key Chapter 6 Algebraic Expressions
Download Go Math Grade 7 Answer Key Chapter 6 Algebraic Expressions pdf on this page. The topics covered in chapter 6 algebraic expressions are combining like terms using the properties. Refer to our Go Math Grade 7 Chapter 6 Algebraic Expression to prove yourself in the exams. Test and enhance your math skills by solving the questions provided at the end of the chapter.
Chapter 6 Algebraic Expressions – Lesson:1
Chapter 6 Algebraic Expressions – Lesson:2
Chapter 6 Algebraic Expressions – Lesson:3
Chapter 6 Algebraic Expressions – Lesson:4
Chapter 6 Algebraic Expressions
Guided Practice – Page No. 176
Question 1.
The manager of a summer camp has 14 baseballs and 23 tennis balls. The manager buys some boxes of baseballs with 12 baseballs to a box and an equal number of boxes of tennis balls with 16 tennis balls to a box. Write an expression to represent the total number of balls.
______ + ______ n
Answer: 37 + 28n
Explanation:
Given that,
The manager of a summer camp has 14 baseballs and 23 tennis balls.
The manager buys some boxes of baseballs with 12 baseballs to a box and an equal number of boxes of tennis balls with 16 tennis balls to a box.
Let n be the number of boxes of each type
Baseballs: 14 + 12n
Tennis Balls: 23 + 16n
Now add the like terms
14 + 12n + 23 + 16n
(14 + 23) + (12 + 16)n
37 + 28n
Thus the expression for the total number of balls is 37 + 28n
Question 2.
Use the expression you found above to find the total number of baseballs and tennis balls if the manager bought 9 boxes of each type.
Answer: 289
Explanation:
The expression we found in the above question is 37 + 28n
n = 9 boxes
Substitute the value of n in the expression
37 + 28(9) = 37 + 252 = 289
Thus the total number of balls = 289
Use the Distributive Property to expand each expression.
Question 3.
0.5(12m – 22n)
______ m – ______ n
Answer: 6m – 11n
Explanation:
We use the Distributive Property to expand the expression.
0.5(12m – 22n) = 0.5(12m) – 0.5(22n)
= 16m – 11n
Thus the expansion of 0.5(12m – 22n) is 16m – 11n
Question 4.
\(\frac{2}{3}\)(18x + 6z)
______ x + ______ z
Answer: 12x + 4z
Explanation:
We use the Distributive Property to expand the expression.
\(\frac{2}{3}\)(18x + 6z) = \(\frac{2}{3}\)(18x) + \(\frac{2}{3}\)(6z)
= \(\frac{36}{3}\) + \(\frac{12}{3}\)
= 12x + 4z
Thus the expansion of \(\frac{2}{3}\)(18x + 6z) is 12x + 4z
Factor each expression.
Question 5.
2x + 12
Type below:
_____________
Answer: 2(x + 6)
Explanation:
The common factor is 2. We factor the expression,
2x + 12 = 2(x + 6)
Question 6.
12x + 24
Type below:
_____________
Answer: 12(x + 2)
Explanation:
The common factor is 12. We factor the expression,
12x + 24 = 12(x + 2)
Question 7.
7x + 35
Type below:
_____________
Answer: 7(x + 5)
Explanation:
The common factor is 7. We factor the expression,
7x + 35 = 7(x + 5)
Essential Question Check-In
Question 8.
What is the relationship between multiplying and factoring?
Answer:
Factoring a number means writing it as a product – a list of numbers which when multiplied, give you the original number, thus factoring implies multiplication.
On the other hand, we can interpret the relationship between factoring and multiplication as one opposition because factoring an expression means dividing each term of the expression by the same number/factor.
Independent Practice – Page No. 177
Write and simplify an expression for each situation.
Question 9.
A company rents out 15 food booths and 20 game booths at the county fair. The fee for a food booth is $100 plus $5 per day. The fee for a game booth is $50 plus $7 per day. The fair lasts for d days, and all the booths are rented for the entire time. Write and simplify an expression for the amount in dollars that the company is paid.
______ + ______ d
Answer: 2500 + 215d
Explanation:
Given that,
A company rents out 15 food booths and 20 game booths at the county fair.
The fee for a food booth is $100 plus $5 per day.
The fee for a game booth is $50 plus $7 per day.
Let d be the number of days for which the booths are rented.
We have to write the expression for the amount of money for the food booths
15(100 + 5d)
We have to write the expression for the amount of money for the game booths
20(50 + 7d)
We have to write the expression for the amount of money for all the booths
15(100 + 5d) + 20(50 + 7d)
1500 + 75d + 1000 + 140d
Combine the like terms
2500 + 215d
Thus the expression for the amount in dollars that the company is paid is 2500 + 215d
Question 10.
A rug maker is using a pattern that is a rectangle with a length of 96 inches and a width of 60 inches. The rug maker wants to increase each dimension by a different amount. Let l and w be the increases in inches of the length and width. Write and simplify an expression for the perimeter of the new pattern.
______ + ______ l + ______ w
Answer:
A rug maker is using a pattern that is a rectangle with a length of 96 inches and a width of 60 inches. The rug maker wants to increase each dimension by a different amount.
The formula for the perimeter of a rectangle is 2 Length+ 2 Width
2 ×(96+l+60+w)
=2×(156+l+w)
=(312+2l+2w) inches
In 11 – 12, identify the two factors that were multiplied together to form the array of tiles. Then identify the product of the two factors.
Question 11.

______ x + ______
Answer: 3x + 6
Explanation:
The two factors are
Width = 3
Length = x + 2
The area is the product of the two numbers:
3(x + 2) = 3(x) + 3(2)
3x + 6
Question 12.

______ x – ______
Answer: 8x – 4
Explanation:
The two factors are
Width = 4
Length = 2x – 1
The area is the product of the two numbers:
4(2x – 1) = 4(2x) + 4(-1) = 8x – 4
Question 13.
Explain how the figure illustrates that 6(9) = 6(5) + 6(4).
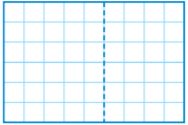
Type below:
___________
Answer:
Note that the left part of the figure has 6 units from top to bottom and 5 units from left to right making it 6 × 5. On the other hand, the right part has also 6 units from top to bottom but 4 units from left to right making it 6 × 4. Adding the two expressions will give (6 × 5) + (6 × 4).
In 14–15, the perimeter of the figure is given. Find the length of the indicated side.
Question 14.
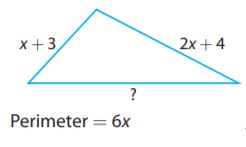
Type below:
_____________
Answer: 3x – 7
Explanation:
We know that the perimeter of a figure is the sum of all sides. Therefore, we can identify the length of the other side by representing it with a variable, s
side + side + side = perimeter
s + (x + 3) + (2x +4) = 6x
s + 3x + 7 = 6x
s = 6x – 3x – 7
Combine the like terms
s = 3x – 7
Question 15.
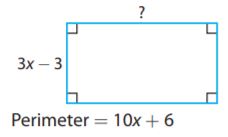
Type below:
_____________
Answer: 2x + 6
Explanation:
We know that the perimeter of a figure is the sum of all sides. Therefore, we can identify the length of the other side by representing it with a variable, s
2side + 2side = perimeter
2s + 2(3x – 3) = 10x + 6
2s + 6x – 6 = 10x + 6
2s = 10x + 6 -6x + 6
2s = 4x + 12
2s = 2(2x+ 6)
s = 2x + 6
Page No. 178
Question 16.
Persevere in Problem Solving
The figures show the dimensions of a tennis court and a basketball court given in terms of the width x in feet of the tennis court.
a. Write an expression for the perimeter of each court.
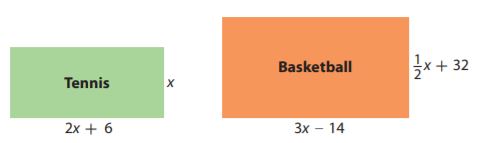
Type below:
_____________
Answer:
Since the courts are rectangle, we can add all sides of the court using the given expressions:
Tennis:
x + x + (2x + 6) + (2x + 6)
= 2x + 4x + 12
= 6x + 12
Basketball:
(1/2 x + 32) + (1/2 x + 32) + (3x – 14) + (3x – 14)
x + 64 + 6x – 28
Now combine the like terms
7x + 36
Question 16.
b. Write an expression that describes how much greater the perimeter of the basketball court is than the perimeter of the tennis court.
Type below:
_____________
Answer: x + 24
Explanation:
Since the perimeter of the basketball court is larger, we subtract the perimeter of the tennis court from this.
Therefore the expression is (7x + 36) – (6x + 12)
= 7x + 36 – 6x – 12 = x + 24
Question 16.
c. Suppose the tennis court is 36 feet wide. Find all dimensions of the two courts.
Width of the tennis court: _________ feet
Length of the tennis court: _________ feet
Width of basketball court: _________ feet
Length of the basketball court: _________ feet
Answer:
To find all dimensions, we substitute 36 in x of the tennis court and solve for the length.
For the tennis court:
Width: x = 36 feet
Length: 2x + 6 = 2(36) + 6 = 72 + 6 = 78 feet
For the basketball court:
Width: 1/2 x + 32 = 1/21(36) + 32 = 18 + 32 = 50 feet
Length: 3x – 14 = 3(36) – 14 = 108 – 14 = 94 feet
Question 17.
Draw Conclusions
Use the figure to find the product (x + 3)(x + 2). (Hint: Find the area of each small square or rectangle, then add.)
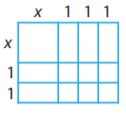
Type below:
_____________
Answer: x² + 5x + 6
Explanation:
We can add the area of the smaller squares to find the area of the entire figure.
Note that there is one x.x = x²
There are 3(x.1) = 3x
There are 2(x.1) = 2x
There are 6(1.1) = 6
Adding these together we get x² + 3x + 2x + 6 = x² + 5x + 6
Question 18.
Communicate Mathematical Ideas
Desmond claims that the product shown at the right illustrates the Distributive Property. Do you agree? Explain why or why not.
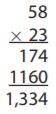
________
Answer: Yes
Explanation:
The multiplication can be written:
58 × 23 = 58(20 + 3)
58(20) + 58(3)
1160 + 174
We notice that the products 174 and 1160 were obtained using the Distributive Property.
Question 19.
Justify Reasoning
Describe two different ways that you could find the product 8 × 997 using mental math. Find the product and explain why your methods work.
Type below:
_____________
Answer:
We are given the product
8 × 997
For a mental computation, we use the fact that 997 is close to 1000
8 × 997 = 8 . (1000 – 3)
8 × 1000 – 8 × 3
8000 – 24
7976
Other method:
8 × 997 = 8 . (900 + 90 + 7)
8(900) + 8(90) + 8(7)
7200 + 720 + 56
7976
Guided Practice – Page No. 182
The table shows the average temperature in Barrow, Alaska, for three months during one year.
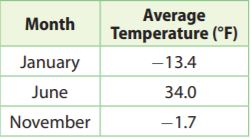
Question 1.
How many degrees warmer is the average temperature in November than in January?
________ °F
Answer: 11.7°F
Explanation:
Let x represent the number of degrees the temperature in November is warmer than in January.
x + (-13.4) = -1.7
x – 13.4 + 13.4 = -1.7 + 3.4
x = 11.7
Thus the average temperature in November is 11.7°F warmer.
Question 2.
Suppose that during one period of extreme cold, the average daily temperature decreased 1 \(\frac{1}{2}\) °F each day. How many days did it take for the temperature to decrease by 9 °F?
________ days
Answer: 6 days
Explanation:
Let x be the number of days it took for the temperature to decrease by 9 °F
(-1 1/2)x = -9
-3/2x = -9
-3x = -18
x = 6
It took 6 days for the temperature to decrease by 9°F.
Use inverse operations to solve each equation.
Question 3.
−2x = 34
________
Answer: -17
Explanation:
We are given the equation:
−2x = 34
x = -17
Question 4.
y − 3.5 = −2.1
________
Answer: 1.4
Explanation:
We are given the equation:
y − 3.5 = −2.1
y = -2.1 + 3.5
y = 1.4
Question 5.
\(\frac{2}{3}\) z = −6
________
Answer: -9
Explanation:
We are given the equation:
\(\frac{2}{3}\) z = −6
z = -6 × \(\frac{3}{2}\)
z = -9
Essential Question Check-In
Question 6.
How does writing an equation help you solve a problem?
Type below:
_____________
Answer:
Writing an equation helps us model a problem. Once the equation is written, we can apply mathematical rules to determine the unknown in the equation.
Independent Practice – Page No. 183
The table shows the elevation in feet at the peaks of several mountains. Use the table for 7–9.
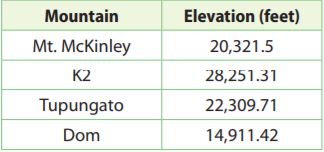
Question 7.
Mt. Everest is 8,707.37 feet higher than Mt. McKinley. What is the elevation of Mt. Everest?
________ feet
Answer: 29,087.87
Explanation:
Given that,
Mt. Everest is 8,707.37 feet higher than Mt. McKinley.
Add 8707.37 to the height of the Mt. McKinley to find the height of the Mt. Everest.
20,321.5 + 8,707.37 = 29,028.87
Thus the elevation of Mt. Everest is 29,087.87 feet
Question 8.
Liam descended from the summit of K2 to an elevation of 23,201.06 feet. How many feet did Liam descend? What was his change in elevation?
________ feet
Answer: 5050.25 feet
Explanation:
Given,
Liam descended from the summit of K2 to an elevation of 23,201.06 feet.
Subtract the height of the K2 mountain and his elevation after descending to find the number of feet he descended. Since he descended down the mountain the change in elevation is the negative of the number of feet he descended.
descent: 28,251.31 – 23,201.06 = 5050.25 feet
change in elevation: -5050.25 feet
Question 9.
K2 is 11,194.21 feet higher than Mt. Kenya. Write and solve an equation to find the elevation of Mt. Kenya.
________ feet
Answer: 17,057.1
Explanation:
Let h be the height of Mt. Kenya.
Write the equation using the given information that K2, with a height of 28,251.31 feet, is 11,194.21 feet higher than Mt. Kenya.
h + 11,194.21 = 28, 251.31
h = 17057.1 feet
Question 10.
A hot air balloon begins its descent at a rate of 22 \(\frac{1}{2}\) feet per minute. How long will it take for the balloon’s elevation to change by -315 feet?
________ minutes
Answer: 14 minutes
Explanation:
A hot air balloon begins its descent at a rate of 22 \(\frac{1}{2}\) feet per minute.
315/22 \(\frac{1}{2}\) = 315/\(\frac{45}{2}\)
= 315 × \(\frac{2}{45}\) = 14 minutes
Question 11.
During another part of its flight, the balloon in Exercise 10 had a change in elevation of -901 feet in 34 minutes. What was its rate of descent?
________ \(\frac{□}{□}\) feet per minute
Answer:
Divide the number of feet by the number of minutes
\(\frac{901}{34}\) = 26.5 feet per minute
(Or)
\(\frac{901}{10}\) = 90.1 feet per minute
The table shows the average temperatures in several states from January through March. Use the table for 12–14.
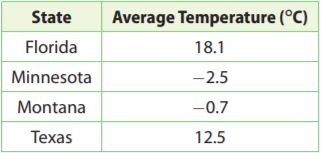
Question 12.
Write and solve an equation to find how much warmer Montana’s average 3-month temperature is than Minnesota’s.
________ °C
Answer: 1.8°C
Explanation:
Write an equation where t is the number of degrees warmer than Montana’s temperature is compared to Minnesota’s
-2.5 + t = -0.7
t = -0.7 + 2.5
t = 1.8°C
Question 13.
How much warmer is Florida’s average 3-month temperature than Montana’s?
________ °C
Answer: 18.8°C
Explanation:
Subtract Florida and Montana’s temperatures
18.1 – (-0.7) = 18.1 + 0.7 = 18.8°C
Question 14.
How would the average temperature in Texas have to change to match the average temperature in Florida?
________ °C
Answer: increase by 5.6°C
Explanation:
Subtract Florida and Texas’s temperatures
18.1 – 12.5 = 5.6 °C
Question 15.
A football team has a net yardage of −26 \(\frac{1}{3}\) yards on a series of plays. The team needs a net yardage of 10 yards to get a first down. How many yards do they have to get on their next play to get a first down?
________ \(\frac{□}{□}\) yards
Answer: 36 \(\frac{1}{3}\) yards
Explanation:
Subtract the final net yardage and the current net yardage to find how many more yards they need
10 – (−26 \(\frac{1}{3}\)) = 10 + 26 \(\frac{1}{3}\)
= 36 \(\frac{1}{3}\)
They have to get 36 \(\frac{1}{3}\) yards on their next play to get the first down.
Page No. 184
Question 16.
A diver begins at sea level and descends vertically at a rate of 2 \(\frac{1}{2}\) feet per second. How long does the diver take to reach -15.6 feet?
________ seconds
Answer: 6.24 seconds
Explanation:
Divide the number of feet the diver descends by the rate of descent.
time = distance/rate
\(\frac{-15.6}{-2.5}\)
= 6.24 seconds
Question 17.
Analyze Relationships
In Exercise 16, what is the relationship between the rate at which the diver descends, the elevation he reaches, and the time it takes to reach that elevation?
Type below:
_____________
Answer: The elevation he reaches (y) is directly proportional to the time it takes to reach that elevation (x) and the rate of descent is (k) the constant of proportionality.
Question 18.
Check for Reasonableness
Jane withdrew money from her savings account in each of 5 months. The average amount she withdrew per month was $45.50. How much did she withdraw in all during the 5 months? Show that your answer is reasonable.
$ ________
Answer: $227.50
Explanation:
Multiply the amount she withdrew per month by the number of months.
45.50 × 5 = 227.50
Since 45.50 ≈ 50 and 50 × 5 = 250 which is close to 227.50, the answer is reasonable.
Question 19.
Justify Reasoning
Consider the two problems below. Which values in the problems are represented by negative numbers? Explain why.
(1) A diver below sea level ascends 25 feet to a reef at -35.5 feet. What was the elevation of the diver before she ascended to the reef?
(2) A plane descends 1.5 miles to an elevation of 3.75 miles. What was the elevation of the plane before its descent?
Type below:
_____________
Answer:
The elevation of -35.5 and the elevation after ascending are both represented by the negative numbers. The change in elevation is represented by a negative number since the plane is descending.
Question 20.
Analyze Relationships
How is solving -4x = -4.8 different from solving − \(\frac{1}{4}\) x = -4.8? How are the solutions related?
Type below:
_____________
Answer:
When you are solving -4x = -4.8, you are dividing both sides by -4 to solve for x.
When you are solving − \(\frac{1}{4}\) x = -4.8, you are multiplying both sides by -4 to solve for x.
The answers for the second equation is then 16 times the answer to the first problem since 4 × 4 = 16
Question 21.
Communicate Mathematical Ideas
Flynn opens a savings account. In one 3-month period, he makes deposits of $75.50 and $55.25. He makes withdrawals of $25.15 and $18.65. His balance at the end of the 3-month period is $210.85. Explain how you can find his initial deposit amount.
$ ________
Answer: $123.90
Explanation:
Let x be his initial deposit. Write the equation for his balance after making the additional deposits and withdrawals.
x + 75.50 + 55.25 – 25.15 – 18.65 = 210.58
x + 86.95 = 210.85
Simplify the left side of the equation
x = 123.90
Thus the initial deposit amount is $123.90
Guided Practice – Page No. 188
Draw algebra tiles to model the given two-step equation.
Question 1.
2x + 5 = 7
Type below:
_____________
Answer: 1
Explanation:
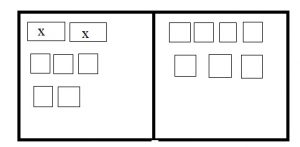
First, draw two positive rectangles on the left to represent 2x and five positive squares to represent 5. One the right side, draw 7 positive squares to represent 7.
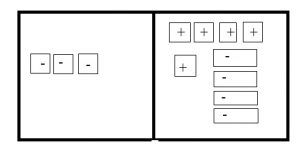
Question 2.
−3 = 5 − 4x
Type below:
_____________
Answer: 2
Explanation:
Draw 3 negative squares on the left side to represent -3. On the right side, draw 5 positive squares to represent 5 and 4 negative rectangles to represent -4x.
Question 3.
A group of adults plus one child attend a movie at Cineplex 15. Tickets cost $9 for adults and $6 for children. The total cost for the movie is $78. Write an equation to find the number of adults in the group.
________ adults
Answer: 8 adults
Explanation:
Given,
A group of adults plus one child attend a movie at Cineplex 15.
Tickets cost $9 for adults and $6 for children.
The total cost for the movie is $78.
Write the equation for the total cost letting a be the number of adults.
9a + 6 = 78
9a = 72
a = 8
Therefore there are 8 adults in the group.
Question 4.
Break down the equation 2x + 10 = 16 to analyze each part.
Type below:
_____________
Answer:
Since x is the value we are trying to find, x is the solution. This means that 2x is the quantity we are looking for multiplied by 2. The 10 is added to 2x = 16 means the result is 16.
Question 5.
Write a corresponding real-world problem to represent 2x – 125 = 400.
Type below:
_____________
Answer:
A real-world problem could be: You are selling lemonade one summer. You paid a total of $125 for all the supplies you needed. If you charge customers $2 per cup of lemonade, how many cups of lemonade do you have to sell to make a profit of $400?
Essential Question Check-In
Question 6.
Describe the steps you would follow to write a two-step equation you can use to solve a real-world problem.
Type below:
_____________
Answer:
First you must define what you are looking for with a variable. In the real-world problem I wrote a problem 5, the variable, x represents the number of cups sold. Next, decide how the remaining information is related to the variable. Since x is the number of cups sold and $2 is the price per cup, then the equation needs to have 2x.
Since profit = income – the cost of supplies, the cost of $125 needs to be subtracted from 2x and the equation needs to equal to the profit of $400. This would give an equation of 2x – 125 = 400.
Independent Practice – Page No. 189
Question 7.
Describe how to model -3x + 7 = 28 with algebra tiles.
Type below:
_____________
Answer:
On the left side, draw 3 negative rectangles to represent -3x and 7 positive squares to represent 7. On the right side, draw 28 positive squares to represent 28.
Question 8.
Val rented a bicycle while she was on vacation. She paid a flat rental fee of $55.00, plus $8.50 each day. The total cost was $123. Write an equation you can use to find the number of days she rented the bicycle.
________ days
Answer: 8 days
Explanation:
Let x be the number of days then the daily fees are 8.50x.
Since there is a flat fee of $55, the total fees are 8.50x + 55
8.50x + 55 = 123
8.50x = 123 – 55
8.50x = 68
x = 68/8.50
x = 8
Thus she rented the bicycle for 8 days.
Question 9.
A restaurant sells a coffee refill mug for $6.75. Each refill costs $1.25. Last month Keith spent $31.75 on a mug and refills. Write an equation you can use to find the number of refills that Keith bought.
________ refills
Answer: 20 refills
Explanation:
Given that,
A restaurant sells a coffee refill mug for $6.75.
Each refill costs $1.25. Last month Keith spent $31.75 on a mug and refills.
Let x represent the number of refills then the total for refills is 1.25x.
Since the cost of the mug was $6.75, the total cost is 6.75 + 1.25x
6.75 + 1.25x = 31.75
1.25x = 31.75 – 6.75
1.25x = 25
x = 25/1.25
x = 20
Thus the number of refills that Keith bought is 20 refills.
Question 10.
A gym holds one 60-minute exercise class on Saturdays and several 45-minute classes during the week. Last week all of the classes lasted a total of 285 minutes. Write an equation you can use to find the number of weekday classes.
________ classes
Answer: 5 classes
Explanation:
Given,
A gym holds one 60-minute exercise class on Saturdays and several 45-minute classes during the week.
Last week all of the classes lasted a total of 285 minutes.
Let x be the number of 45 minute classes then the total time of 45 minute classes if 45x the total time of all classes is then 60 + 45x = 285
45x = 285 – 60
45x = 225
x = 225/45
x = 5
Thus the number of weekday classes is 5.
Question 11.
Multiple Representations
There are 172 South American animals in the Springdale Zoo. That is 45 more than half the number of African animals in the zoo. Write an equation you could use to find n, the number of African animals in the zoo.
________ animals
Answer: 254 animals
Explanation:
There are 172 South American animals in the Springdale Zoo. That is 45 more than half the number of African animals in the zoo.
n/2 + 45 = 172
n/2 = 172 – 45
n/2 = 127
n = 127 × 2
n = 254 animals
Thus the number of African animals in the zoo is 254.
Question 12.
A school bought $548 in basketball equipment and uniforms costing $29.50 each. The total cost was $2,023. Write an equation you can use to find the number of uniforms the school purchased.
________ uniforms
Answer: 50 uniforms
Explanation:
The total cost is equal to the cost of the basketball equipment plus the cost of the uniforms.
Let x represent the number of uniforms. Since each uniform costs $29.50, then the cost of x uniforms is 29.50x dollars.
The cost of the basketball equipment is $548 so the total cost is 548 + 29.50x
It is given that the total cost is $2023 so setting this equal to the expression we obtained for the total cost gives the equation 548 + 29.50x = 2023
29.50x = 2023 – 548
29.50x = 1475
x = 1475/29.50
x = 50
Thus the number of uniforms the school purchased is 50.
Question 13.
Financial Literacy
Heather has $500 in her savings account. She withdraws $20 per week for gas. Write an equation Heather can use to see how many weeks it will take her to have a balance of $220.
________ weeks
Answer: 14 weeks
Explanation:
Given,
Heather has $500 in her savings account. She withdraws $20 per week for gas.
Let x be the number of weeks. Since she is withdrawing $20 each week, then after x weeks her account has changed by -20x dollars.
Her original balance was $500 so after x weeks, her ending balance is 500 – 20x dollars.
It is given that her ending balance is $220 so the equation is
500 – 20x = 220
-20x = 220 – 500
-20x = -280
x = 280/20
x = 14
It will take 14 weeks to have a balance of $220.
Question 14.
Critique Reasoning
For 9x + 25 = 88, Deena wrote the situation “I bought some shirts at the store for $9 each and received a $25 discount. My total bill was $88. How many shirts did I buy?”
a. What mistake did Deena make?
Type below:
_____________
Answer: Her mistake was that a discount would decrease the amount she paid so her equation should have 25 subtracted, not added.
Question 14.
b. Rewrite the equation to match Deena’s situation.
Type below:
_____________
Answer: Changing the addition in 9x + 25 = 88 to subtraction gives 9x – 25 = 88
Question 14.
c. How could you rewrite the situation to make it fit the equation?
Type below:
_____________
Answer: Instead of a discount, the situation could be rewritten to have her buying another item, like pants or a sweater, that cost $25.
Page No. 190
Question 15.
Multistep
Sandy charges each family that she babysits a flat fee of $10 for the night and an extra $5 per child. Kimmi charges $25 per night, no matter how many children a family has.
a. Write a two-step equation that would compare what the two girls charge and find when their fees are the same.
Type below:
_____________
Answer: 10 + 5x = 25
Explanation:
Let x be the number of children.
Sandy charges each family that she babysits a flat fee of $10 for the night and an extra $5 per child. Kimmi charges $25 per night, no matter how many children a family has.
This means that she charges a total of 10 + 5x per night.
Kimmi only charges a flat fee of $25 per night,
Since you need to compare their charges, set these expressions equal to each other.
Sandy: 10 + 5x
Kimmi: 25
The equation is 10 + 5x = 25
Question 15.
b. How many children must a family have for Sandy and Kimmi to charge the same amount?
________ children
Answer: 3 children
Explanation:
Subtract 10 on both sides and then divide both sides by 5 to solve for x.
10 + 5x = 25
5x = 25 – 10
5x = 15
x = 3 children
Question 15.
c. The Sanderson family has five children. Which babysitter should they choose if they wish to save some money on babysitting, and why?
_____________
Answer: Kimmi, saves them $10
Explanation:
Substitute x = 5 in the above equation for Sandy.
10 + 5(5) = 10 + 25 = 35
This is $10 more than the $25 that Kimmi Charges so they should choose Kimmi because it will save them $10.
H.O.T.
Focus on Higher Order Thinking
Question 16.
Analyze Relationships
Each student wrote a two-step equation. Peter wrote the equation 4x – 2 = 10, and Andres wrote the equation 16x – 8 = 40. The teacher looked at their equations and asked them to compare them. Describe one way in which the equations are similar.
Type below:
_____________
Answer:
Each student wrote a two-step equation. Peter wrote the equation 4x – 2 = 10, and Andres wrote the equation 16x – 8 = 40.
4x – 2 = 10
4x = 10 + 2
4x = 12
x = 3
16x – 8 = 40
16x = 40 + 8
16x = 48
x = 48/16
x = 3
They are also similar because if you multiply both sides of 4x – 2 = 10 by 4, you get 16x – 8 = 40
Question 17.
What’s the Error?
Damon has 5 dimes and some nickels in his pocket, worth a total of $1.20. To find the number of nickels Damon has, a student wrote the equation 5n + 50 = 1.20. Find the error in the student’s equation.
Type below:
_____________
Answer:
The error is that he wrote the amount of money on the left side of the equation in cents but wrote the amount of money on the left side of the equation in dollars. He needs to write the equation as either 5n + 50 = 120. or 0.05n + 0.50 = 1.20
Question 18.
Represent Real-World Problems
Write a real-world problem you could answer by solving the equation -8x + 60 = 28.
Type below:
_____________
Answer:
A possible real-world problem could be: You have $60 to spend on clothes. You want to buy some T-shirts that cost $8 each. After you went shopping, you had $28 left. How many T-shirts did you buy?
Guided Practice – Page No. 194
The equation 2x + 1 = 9 is modeled below

Question 1.
To solve the equation with algebra tiles, first remove _____
Then divide each side into _____
Type below:
_____________
Answer:
The first step is to remove one positive square on each side. Then divide each side into 2 equal groups.
Question 2.
The solution is x = _____
x = ______
Answer: x = 4
Explanation:
The solution is x = 4 since removing one square on each side gives 2x = 8 and then dividing each side into two equal groups gives x = 4.
Solve each problem by writing and solving an equation.
Question 3.
A rectangular picture frame has a perimeter of 58 inches. The height of the frame is 18 inches. What is the width of the frame?
______ inches
Answer: 11 inches
Explanation:
A rectangular picture frame has a perimeter of 58 inches. The height of the frame is 18 inches.
The perimeter of a rectangle is P = 2w + 2h.
It is given that the perimeter of the rectangular frame is P = 58 inches and the height is h = 18 inches.
P = 2w + 2h
58 = 2w + 2(18)
2w = 58 – 36
2w = 22
w = 11 inches
Thus the width of the frame is 11 inches.
Question 4.
A school store has 1200 pencils in stock and sells an average of 24 pencils per day. The manager reorders when the number of pencils in stock is 500. In how many days will the manager have to reorder?
______ days
Answer: 30 days
Explanation:
A school store has 1200 pencils in stock and sells an average of 24 pencils per day.
The manager reorders when the number of pencils in stock is 500.
Let x be the number of days
1200 – 24x = 500
-24x = -700
x ≈ 30
Thus the manager has to reorder 30 days.
Essential Question Check-In
Question 5.
How can you decide which operations to use to solve a two-step equation?
Type below:
_____________
Answer:
You must use inverse operations when solving a two-step equation. You remove addition by subtracting the inverse operation of subtraction. You get rid of multiplication by using the inverse operation of division.
Page No. 195
Question 6.
9s + 3 = 57
______
Answer: 6
Explanation:
We are given the equation
9s + 3 = 57
9s = 57 – 3
9s = 54
s = 54/9
s = 6
Question 7.
4d + 6 = 42
______
Answer: 9
Explanation:
We are given the equation
4d + 6 = 42
4d = 42 – 6
4d = 36
d = 36/4
d = 9
Question 8.
−3y + 12 = −48
______
Answer: 20
Explanation:
We are given the equation
−3y + 12 = −48
-3y = -48 – 12
-3y = -60
3y = 60
y = 20
Question 9.
\(\frac{k}{2}\) + 9 = 30
______
Answer: 42
Explanation:
We are given the equation
\(\frac{k}{2}\) + 9 = 30
\(\frac{k}{2}\) = 30 – 9
k/2 = 21
k = 42
Question 10.
\(\frac{g}{3}\) − 7 = 15
______
Answer: 66
Explanation:
We are given the equation
\(\frac{g}{3}\) − 7 = 15
\(\frac{g}{3}\) = 15 + 7
g/3 = 22
g = 22 × 3
g = 66
Question 11.
\(\frac{z}{5}\) + 3 = −35
______
Answer: -190
Explanation:
We are given the equation
\(\frac{z}{5}\) + 3 = −35
\(\frac{z}{5}\) = −35 – 3
z/5 = -38
z = -38 × 5
z = -190
Question 12.
−9h − 15 = 93
______
Answer: -12
Explanation:
We are given the equation
−9h − 15 = 93
-9h = 93 + 15
-9h = 108
-h = 108/9
h = -12
Question 13.
−3(n + 5) = 12
______
Answer: -9
Explanation:
We are given the equation
−3(n + 5) = 12
-3n – 15 = 12
-3n = 12 + 15
-3n = 27
-n = 27/3
n = -9
Question 14.
−17 + \(\frac{b}{8}\) = 13
______
Answer: 240
Explanation:
We are given the equation
−17 + \(\frac{b}{8}\) = 13
b/8 = 13 + 17
b/8 = 30
b = 30 × 8
b = 240
Question 15.
7(c − 12) = −21
______
Answer: 9
Explanation:
We are given the equation
7(c − 12) = −21
7c – 84 = -21
7c = -21 + 84
7c = 63
c = 63/7
c = 9
Question 16.
−3 + \(\frac{p}{7}\) = −5
______
Answer: -14
Explanation:
We are given the equation
−3 + \(\frac{p}{7}\) = −5
\(\frac{p}{7}\) = -5 + 3
\(\frac{p}{7}\) = -2
p = -2 × 7
p = -14
Question 17.
46 = −6t − 8
______
Answer: -9
Explanation:
We are given the equation
46 = −6t − 8
-6t – 8 = 46
-6t = 46 + 8
-6t = 54
-t = 54/6
t = -9
Question 18.
After making a deposit, Puja had $264 in her savings account. She noticed that if she added $26 to the amount originally in the account and doubled the sum, she would get the new amount. How much did she originally have in the account?
$ ______
Answer: $106
Explanation:
Let x be the original amount. Adding $26 to the original amount gives a sum of x + 26.
Doubling the sum then gives 2(x + 26) so the new amount is 2(x + 26) dollars.
It is given that the new amount is $264 so 2(x + 26) = 264
2(x + 26) = 264
x + 26 = 264/2
x + 26 = 132
x = 132 – 26
x = 106
Thus she originally has $106 in the account.
Question 19.
The current temperature in Smalltown is 20 °F. This is 6 degrees less than twice the temperature that it was six hours ago. What was the temperature in Smalltown six hours ago?
______ °F
Answer: 13°F
Explanation:
The current temperature in Smalltown is 20 °F. This is 6 degrees less than twice the temperature that it was six hours ago.
Let x be the temperature six hours ago
2x – 6 = 20
2x = 20 + 6
2x = 26
x = 13
Thus the temperature is 13°F in Smalltown six hours ago.
Question 20.
One reading at an Arctic research station showed that the temperature was -35 °C. What is this temperature in degrees Fahrenheit?
______ °F
Answer: -31°F
Explanation:
One reading at an Arctic research station showed that the temperature was -35 °C.
Substitute C = -35 into the formula for converting Celsius and Fahrenheit temperatures
C = 5/9 (F – 32)
-35 = \(\frac{5}{9}\)(F – 32)
-35 × \(\frac{9}{5}\) = F – 32
-7 × 9 = F – 32
-63 = F – 32
F = -63 + 32
F = -31°F
Thus the temperature in degrees Fahrenheit is -31°F
Question 21.
Artaud noticed that if he takes the opposite of his age and adds 40, he gets the number 28. How old is Artaud?
______ years old
Answer: 12 years old
Explanation:
Artaud noticed that if he takes the opposite of his age and adds 40, he gets the number 28.
Let x be his age
-x + 40 = 28
x = 40 – 28
x = 12
Thus Artaud is 12 years old.
Question 22.
Sven has 11 more than twice as many customers as when he started selling newspapers. He now has 73 customers. How many did he have when he started?
______ costumers
Answer: 31 customers
Explanation:
Let x be the number of customers he started with
11 + 2x = 73
2x = 73 – 11
2x = 62
x = 62/2
x = 31
Thus Sven has 31 customers when he started.
Question 23.
Paula bought a ski jacket on sale for $6 less than half its original price. She paid $88 for the jacket. What was the original price?
$ ______
Answer: $188
Explanation:
Given that,
Paula bought a ski jacket on sale for $6 less than half its original price. She paid $88 for the jacket.
Let x be the original price
1/2 x – 6 = 88
1/2 x = 88 + 6
1/2 x = 94
x = 94 × 2
x = 188
Thus the original price is $188.
Question 24.
The McIntosh family went apple picking. They picked a total of 115 apples. The family ate a total of 8 apples each day. After how many days did they have 19 apples left?
______ days
Answer: 12 days
Explanation:
The McIntosh family went apple picking. They picked a total of 115 apples. The family ate a total of 8 apples each day
Let x be the number of days.
115 – 8x = 19
115 – 19 = 8x
8x = 96
x = 96/8
x = 12
Thus the answer for the above question is 12 days.
Use a calculator to solve each equation.
Question 25.
−5.5x + 0.56 = −1.64
______
Answer: 0.4
Explanation:
We are given the equation
−5.5x + 0.56 = −1.64
Subtract 0.56 on both sides
-5.5x = -2.2
Divide both sides by -5.5
x = 0.4
Question 26.
−4.2x + 31.5 = −65.1
______
Answer: 23
Explanation:
We are given the equation
−4.2x + 31.5 = −65.1
Subtract 31.5 on both sides
-4.2x = -96.6
4.2x = 96.6
x = 96.6/4.2
x = 23
Question 27.
\(\frac{k}{5.2}\) + 81.9 = 47.2
______
Answer: -180.44
Explanation:
We are given the equation
\(\frac{k}{5.2}\) + 81.9 = 47.2
k/5.2 = 47.2 – 81.9
k/5.2 = -34.7
k = -180.44
Page No. 196
Question 28.
Write a two-step equation that involves multiplication and subtraction, includes a negative coefficient, and has a solution of x = 7.
Type below:
____________
Answer:
A possible two-step equation that involves multiplication and subtraction, includes a negative coefficient and has a solution of x = 7 is -2x – 7 = -21
-2x = -21 + 7
-2x = -14
2x = 14
x = 14/2
x = 7
Question 29.
Write a two-step equation involving division and addition that has a solution of x = -25
Type below:
____________
Answer: \(\frac{x}{5}\) + 20 = 15
Explanation:
A possible two-step equation that involves division and addition and has a solution of x = -25 is \(\frac{x}{5}\) + 20 = 15
\(\frac{x}{5}\) = 15 – 20
\(\frac{x}{5}\) = -5
x = -25
Question 30.
Explain the Error
A student’s solution to the equation 3x + 2 = 15 is shown. Describe and correct the error that the student made.
3x + 2 = 15 Divide both sides by 3.
x + 2 = 5 Subtract 2 from both sides.
x = 3
\(\frac{□}{□}\)
Answer:
Her error was when she divided both sides by 3.
She didn’t divide the 2 by 3. She should have gotten x + \(\frac{2}{3}\) = 5 after dividing both sides by 3.
Her first step should have been subtracting both sides by 2 instead of dividing both sides by 3.
3x + 2 = 15
3x = 15 – 2
3x = 13
x = 13/2
Question 31.
Multiple Representations
Explain how you could use the work backward problem-solving strategy to solve the equation \(\frac{x}{4}\) − 6 = 2.
______
Answer: Working backward would mean talking the result of 2 and adding 6 to it to get 8. Then multiplying this by 4 to get 32.
H.O.T.
Focus on Higher Order Thinking
Question 32.
Reason Abstractly
The formula F = 1.8C + 32 allows you to find the Fahrenheit (F) temperature for a given Celsius (C) temperature. Solve the equation for C to produce a formula for finding the Celsius temperature for a given Fahrenheit temperature.
Type below:
____________
Answer:
F = 1.8C + 32
F – 32 = 1.8C
1.8C = F – 32
C = (F – 32)/1.8
Question 33.
Reason Abstractly
The equation P = 2(l + w) can be used to find the perimeter P of a rectangle with length l and width w. Solve the equation for w to produce a formula for finding the width of a rectangle given its perimeter and length.
Type below:
____________
Answer:
P = 2(l + w)
P/2 = l + w
P/2 – l = w
w = P/2 – l
Question 34.
Reason Abstractly
Solve the equation ax + b = c for x.
Type below:
____________
Answer:
Subtract both sides by b
ax = c – b
x = (c – b)/a
6.1 Algebraic Expressions – Page No. 197
Question 1.
The Science Club went on a two-day field trip. The first day the members paid $60 for transportation plus $15 per ticket to the planetarium. The second day they paid $95 for transportation plus $12 per ticket to the geology museum. Write an expression to represent the total cost for two days for the n members of the club.
Type below:
____________
Answer: 155 + 27n
Explanation:
Let n be the number of members. Then n also represents the number of tickets.
For the first day, tickets are $15 each so for n members, the ticket cost is 15n dollars. The members must also pay $60 for transportation so the total cost for the first day is 60 + 15n dollars.
For the second day, tickets are $12 each so for n members, the ticket cost is 12n dollars. The members must also pay $95 for transportation so the total cost for the first day is 95 + 12n dollars.
The total cost for the two days is then (60 + 15n) + (95 + 12n).
Combine the like terms.
27n + 155
6.2 One-Step Equations with Rational Coefficients
Solve.
Question 2.
h + 9.7 = −9.7
______
Answer: h = -19.4
Explanation:
We are given the equation
h + 9.7 = −9.7
h = -9.7 – 9.7
h = -19.4
Question 3.
\(-\frac{3}{4}+p=\frac{1}{2}\)
\(\frac{□}{□}\)
Answer: p = 1 \(\frac{1}{4}\)
Explanation:
We are given the equation
\(-\frac{3}{4}+p=\frac{1}{2}\)
-3/4 + p = 1/2
p = 1/2 + 3/4
p = 1 \(\frac{1}{4}\)
Question 4.
−15 = −0.2k
______
Answer: k = 75
Explanation:
We are given the equation
−15 = −0.2k
0.2k = 15
k = 15/0.2
k = 150/2
k = 75
Question 5.
\(\frac{y}{-3}=\frac{1}{6}\)
\(\frac{□}{□}\)
Answer: y = – \(\frac{1}{2}\)
Explanation:
We are given the equation
\(\frac{y}{-3}=\frac{1}{6}\)
y = -3/6
y = -1/2
Question 6.
−\(\frac{2}{3}\) m = −12
______
Answer: m = 18
Explanation:
We are given the equation
−\(\frac{2}{3}\) m = −12
\(\frac{2}{3}\) m = 12
m = 12 × 3/2
m = 6 × 3
m = 18
Question 7.
2.4 = −\(\frac{t}{4.5}\)
______
Answer: t = -10.8
Explanation:
We are given the equation
2.4 = −\(\frac{t}{4.5}\)
-t = 2.4 × 4.5
t = -10.8
6.3 Writing Two-Step Equations
Question 8.
Jerry started doing sit-ups every day. The first day he did 15 sit-ups. Every day after that he did 2 more sit-ups than he had done the previous day. Today Jerry did 33 sit-ups. Write an equation that could be solved to find the number of days Jerry has been doing sit-ups, not counting the first day.
______ days
Answer: 2x + 15 = 33
Explanation:
Let x be the number of days then the number of additional sit-ups is 2x since he does 2 more sit-ups for each day, not counting the first day.
Since he started doing 15 sit-ups on the first day, the total number of sit-ups after x would be 2x +15
2x + 15 = 33
6.4 Solving Two-Step Equations
Solve.
Question 9.
5n + 8 = 43
______
Answer: n = 7
Explanation:
We are given the equation
5n + 8 = 43
5n = 43 – 8
5n = 35
n = 35/5
n = 7
Question 10.
\(\frac{y}{6}\) − 7 = 4
______
Answer: y = 66
Explanation:
We are given the equation
\(\frac{y}{6}\) − 7 = 4
\(\frac{y}{6}\) = 4 + 7
\(\frac{y}{6}\) = 11
y = 11 × 6
y = 66
Question 11.
8w − 15 = 57
______
Answer: w = 9
Explanation:
We are given the equation
8w − 15 = 57
8w = 57 + 15
8w = 72
w = 72/8
w = 9
Question 12.
\(\frac{g}{3}\) + 11 = 25
______
Answer: g = 42
Explanation:
We are given the equation
\(\frac{g}{3}\) + 11 = 25
\(\frac{g}{3}\) = 25 – 11
\(\frac{g}{3}\) = 14
g = 14 × 3
g = 42
Question 13.
\(\frac{f}{5}\) − 22 = −25
______
Answer: f = -15
Explanation:
We are given the equation
\(\frac{f}{5}\) − 22 = −25
\(\frac{f}{5}\) = -25 + 22
\(\frac{f}{5}\) = -3
f = -3 × 5
f = -15
Question 14.
−4p + 19 = 11
______
Answer: p = 2
Explanation:
We are given the equation
−4p + 19 = 11
-4p = 11 – 19
-4p = -8
p = 2
Essential Question
Question 15.
How can you use two-step equations to represent and solve real-world problems?
Type below:
___________
Answer:
You can step two-step equations to represent and solve real-world problems by translating the words into an algebraic equation, solving the equation, and then interpreting the solution to the equation.
Selected Response – Page No. 198
Question 1.
A taxi cab costs $1.50 for the first mile and $0.75 for each additional mile. Which equation could be solved to find how many miles you can travel in a taxi for $10, given that x is the number of additional miles?
Options:
a. 1.5x + 0.75 = 10
b. 0.75x + 1.5 = 10
c. 1.5x − 0.75 = 10
d. 0.75x − 1.5 = 10
Answer: 0.75x + 1.5 = 10
Explanation:
Let x be the number of additional miles then the charge for the additional miles is 0.75x the total cost is then 1.50 + 0.75x = 10
Thus the correct answer is option B.
Question 2.
Which is the solution of \(\frac{t}{2.5}\) = −5.2?
Options:
a. -13
b. -2.08
c. 2.08
d. 13
Answer: -13
Explanation:
t/2.5 = -5.2
t = -5.2 × 2.5
t = -13
Thus the correct answer is option is A.
Question 3.
Which expression is equivalent to 5x − 30?
Options:
a. 5(x − 30)
b. 5(x − 6)
c. 5x(x − 6)
d. x(5 − 30)
Answer: 5(x − 6)
Explanation:
Factor out 5 from each term.
5x – 30 = 5(x – 6)
Thus the correct answer is option B.
Question 4.
In a science experiment, the temperature of a substance is changed from 42 °F to -54 °F at an average rate of -12 degrees per hour. Over how many hours does the change take place?
Options:
a. -8 hours
b. 18 hour
c. 1 hour
d. 8 hours
Answer: 8 hours
Explanation:
In a science experiment, the temperature of a substance is changed from 42 °F to -54 °F at an average rate of -12 degrees per hour.
Let x be the number of hours.
42 – 12x = -54
-12x = -54 – 42
-12x = -96
12x = 96
x = 96/12
x = 8 hours
Thus the correct answer is option D.
Question 5.
Which statement best represents the distance on a number line between -14 and -5?
Options:
a. −14 − (−5)
b. −14 + (−5)
c. −5 − (−14)
d. −5 + (−14)
Answer: −5 − (−14)
Explanation:
Distance is the difference between the biggest number and the smallest number so the distance between -5 and -14 is -5 – (-14) since -5 bigger than -14.
Thus the correct answer is option C.
Question 6.
Which cereal costs the most per ounce?
Options:
a. $4.92 for 12 ounces
b. $4.25 for 10 ounces
c. $5.04 for 14 ounces
d. $3.92 for 8 ounces
Answer: $3.92 for 8 ounces
Explanation:
Find the unit rates for each answer choice by dividing the cost by the number of ounces and rounding to two decimal places if necessary.
a. $4.92 for 12 ounces
4.92/12 = $0.41 per ounce
b. $4.25 for 10 ounces
4.25/10 ≈ 0.43 per ounce
c. $5.04 for 14 ounces
5.04/14 = 0.36 per ounce
d. $3.92 for 8 ounces
3.92/8 = 0.49 per ounce
Thus the correct answer is option D.
Mini-Task
Question 7.
Casey bought 9 tickets to a concert. The total charge was $104, including a $5 service charge.
a. Write an equation you can solve to find c, the cost of one ticket.
Type below:
_____________
Answer: 9c + 5 = 104
Explanation:
Let c be the cost of each ticket, the total cost of 9 tickets before the service charge is 9c adding the service charge gives a total charge of 9c + 5
Question 7.
b. Explain how you could estimate the solution of your equation.
Type below:
_____________
Answer:
104 is about 105. subtracting 5 from this gives 100. 9 is about 10 and 100 divided by 10 is 10 so the ticket price is around $10.
Question 7.
c. Solve the equation. How much did each ticket cost?
$ ______
Answer:
9c = 99
c = 99/9
c = 11
Final Words:
I hope the details mentioned in this article is beneficial for all the students of 7th standard. Enhance your math skills by practicing the problems from HMH Go Math Grade 7 Chapter 6 Algebraic Expressions. Download the Go Math Grade 7 Key Algebraic Expressions pdf and share it with your besties. All the Best Guys!!!
