Go Math Grade 7 Answer Key Chapter 3 Rational Numbers

Get expert verified solutions in Go Math Grade 7 Answer Key Chapter 3 Rational Numbers here. So, the students of the 7th class can Download Go Math Grade 7 Answer Key Chapter 3 Rational Numbers pdf for free. Our Go Math 7th Grade Chapter 3 Rational Numbers helps the students to complete their homework in time and also score the highest marks in the exams.

Go Math Grade 7 Answer Key Chapter 3 Rational Numbers

All concepts are covered in one place along with answers for Go Math Grade 7 Chapter 3 Rational Numbers. Follow the steps to Download HMH Go Math Chapter 3 Grade 7 Answer Key pdf to learn simple methods to solve the problems. The quick way of solving problems will help the students to save time. Hence, check the question and find out the complete answers and explanations for every problem.

Chapter 3 – Rational Numbers and Decimals

• Rational Numbers and Decimals – Guided Practice – Page No. 64
• Rational Numbers and Decimals – Independent Practice – Page No. 65
• Rational Numbers and Decimals – Page No. 66

Chapter 3 – Adding Rational Numbers

• Adding Rational Numbers – Guided Practice – Page No. 72
• Adding Rational Numbers – Independent Practice – Page No. 73
• Adding Rational Numbers – Independent Practice – Page No. 74

Chapter 3 – Subtracting Rational Numbers

• Subtracting Rational Numbers – Guided Practice – Page No. 79
• Subtracting Rational Numbers – Independent Practice – Page No. 80
• Subtracting Rational Numbers – Page No. 81
• Subtracting Rational Numbers – H.O.T – Page No. 82

Chapter 3 – Multiply Rational Numbers

• Multiply Rational Numbers – Guided Practice – Page No. 86
• Multiply Rational Numbers – Independent Practice – Page No. 87
• Multiply Rational Numbers – Page No. 88

Chapter 3 – Divide Rational Numbers

• Divide Rational Numbers – Guided Practice – Page No. 92
• Divide Rational Numbers – Independent Practice – Page No. 93
• Divide Rational Numbers – Page No. 94

Chapter 3 – Applying Rational Number Operations

• Applying Rational Number Operations – Guided Practice – Page No. 98
• Applying Rational Number Operations – Independent Practice – Page No. 99
• Applying Rational Number Operations – Page No. 100

Chapter 3 – Module Review

• Module Quiz – 3.1 Rational Numbers and Decimals – Page No. 101
• MODULE 3 MIXED REVIEW – Selected Response – Page No. 102
• Module 3 Review – Rational Numbers – Page No. 106

Chapter 3 – Performance Tasks

• Unit 1 Performance Tasks – Page No. 107
• Unit 1 Performance Tasks – Page No. 108

Chapter 3 – MIXED REVIEW

• Unit 1 MIXED REVIEW – Selected Response – Page No. 109
• Unit 1 MIXED REVIEW – Page No. 110

Rational Numbers and Decimals – Guided Practice – Page No. 64

Write each rational number as a decimal. Then tell whether each decimal is a terminating or a repeating decimal.

Question 1.
\(\frac{3}{5}\) =
___________ decimals

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.

\(\frac{3}{5}\) = 3 ÷ 5
3/5 = 0.6
The decimal is not repeating so it is a terminating decimal which is 0.6

Question 2.
\(\frac{89}{100}\) =
___________ decimals

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{89}{100}\) = 0.89
The decimal is not repeating so it is a terminating decimal which is 0.89

Question 3.
\(\frac{4}{12}\) =
___________ decimals

Answer: repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{4}{12}\) = 4 ÷ 12
4/12 = 0. 333….
The quotient is a repeating decimal which is 0.33…

Question 4.
\(\frac{25}{99}\) =
___________ decimals

Answer: repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{25}{99}\) = 0.2525…
The quotient is a repeating decimal which is 0.2525…

Question 5.
\(\frac{7}{9}\) =
___________ decimals

Answer: repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{7}{9}\) = 0.77…
The quotient is a repeating decimal which is 0.77…

Question 6.
\(\frac{9}{25}\) =
___________ decimals

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{9}{25}\) = 0.36
The decimal is not repeating so it is a terminating decimal which is 0.36

Question 7.
\(\frac{1}{25}\) =
___________ decimals

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{1}{25}\) = 0.04
The decimal is not repeating so it is a terminating decimal which is 0.04

Question 8.
\(\frac{25}{176}\) =
___________ decimals

Answer: repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{25}{176}\) = 0.14204545454
The quotient is a repeating decimal which is 0.14204545454

Question 9.
\(\frac{12}{1000}\) =
___________ decimals

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{12}{1000}\) =0.012
The decimal is not repeating so it is a terminating decimal which is 0.012

Write each mixed number as a decimal.

Question 10.
11 \(\frac{1}{6}\) =
___________ decimals

Answer: repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
11 \(\frac{1}{6}\) = 11.1666666667
The quotient is a repeating decimal which is 11.1666666667

Question 11.
2 \(\frac{9}{10}\) =
___________ decimals

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
First, convert the mixed fraction to the improper fraction.
2 \(\frac{9}{10}\) = \(\frac{29}{10}\) = 2.9
Thus, the decimal is not repeating so it is a terminating decimal which is 2.9

Question 12.
8 \(\frac{23}{100}\) =
___________ decimals

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
First, convert the mixed fraction to the improper fraction.
8 \(\frac{23}{100}\) = \(\frac{823}{100}\) = 8.23
Thus, the decimal is not repeating so it is a terminating decimal which is 8.23

Question 13.
7 \(\frac{3}{15}\) =
___________ decimals

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
First, convert the mixed fraction to the improper fraction.
7 \(\frac{3}{15}\) = \(\frac{108}{15}\) = 7.2
Thus, the decimal is not repeating so it is a terminating decimal which is 7.2

Question 14.
54 \(\frac{3}{11}\) =
___________ decimals

Answer: repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
First, convert the mixed fraction to the improper fraction.
54 \(\frac{3}{11}\) = \(\frac{597}{11}\) = 54.2727…
The quotient is a repeating decimal which is 54.2727…

Question 15.
3 \(\frac{1}{18}\) =
___________ decimals

Answer: repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
First, convert the mixed fraction to the improper fraction.
3 \(\frac{1}{18}\) = \(\frac{55}{18}\) = 3.055..
The quotient is a repeating decimal which is 3.055..

Question 16.
Maggie bought 3 \(\frac{2}{3}\) lb of apples to make some apple pies. What is the weight of the apples written as a decimal?
3 \(\frac{2}{3}\) =
___________ decimal

Answer: repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
First, convert the mixed fraction to the improper fraction.
3 \(\frac{2}{3}\) = \(\frac{11}{3}\) = 3.66..
The quotient is a repeating decimal which is 3.66..

Question 17.
Harry’s dog weighs 12 \(\frac{7}{8}\) pounds. What is the weight of Harry’s dog written as a decimal?
12 \(\frac{7}{8}\) =
___________ decimals

Answer: terminating

Explanation:
Given that,
Harry’s dog weighs 12 \(\frac{7}{8}\) pounds.
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
First, convert the mixed fraction to the improper fraction.
12 \(\frac{7}{8}\) = \(\frac{103}{8}\) = 12.875

Essential Question Check-In

Question 18.
Tom is trying to write \(\frac{3}{47}\) as a decimal. He used long division and divided until he got the quotient 0.0638297872, at which point he stopped. Since the decimal doesn’t seem to terminate or repeat, he concluded that \(\frac{3}{47}\) is not rational. Do you agree or disagree? Why?
___________

Answer: disagree

Explanation:
We are given the number:
{0, 1, 2, 3, ……45, 46}
When dividing a number by 47 the possible remainders at each step are:
This means that after at most 47 steps we get a remainder which repeats. This means that process and which repeats. This means that the process stops and we get a repeating decimal.

Rational Numbers and Decimals – Independent Practice – Page No. 65

Use the table for 19–23. Write each ratio in the form \(\frac{a}{b}\) and then as a decimal. Tell whether each decimal is a terminating or a repeating decimal.

Question 19.
Basketball players to football players
___________ decimal

Answer: Repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
Since the item is asking us to write basketball players to football players, we write the number of basketball players (5) in the numerator and the number of football players (11) in the denominator.
5/11 = 0.4545..
This is a repeating decimal with 45 as the repeating digits.

Question 20.
Hockey players to lacrosse players
___________ decimal

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
Since the item is asking us to write hockey players to lacrosse players, we write the number of hockey players (6) in the numerator and the number of lacrosse players (10) in the denominator.
Now convert the fraction into the decimal
6/10 = 0.6
This is a terminating decimal which is 0.6.

Question 21.
Polo players to football players
___________ decimal

Answer: Repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
Since the item is asking us to write polo players to football players, we write the number of polo players (4) in the numerator and the number of football players (11) in the denominator.
Now we convert this as a decimal.
4/11 = 0.36..
This is a repeating decimal with 36 as the repeating digits.

Question 22.
Lacrosse players to rugby players
___________ decimal

Answer: Repeating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
Since the item is asking us to write lacrosse players to rugby players, we write the number of lacrosse players (10) in the numerator and the number of rugby players (15) in the denominator.
10/15 = 0.66..
This is a repeating decimal with 6 as the repeating digit.

Question 23.
Football players to soccer players
___________ decimal

Answer: terminating

Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits
Since the item is asking us to write football players to soccer players, we write the number of football players (11) in the numerator and the number of soccer players (11) in the denominator.
11/11 = 1
This is a terminating decimal which is 1.

Question 24.
Look for a Pattern Beth said that the ratio of the number of players in any sport to the number of players on a lacrosse team must always be a terminating decimal. Do you agree or disagree? Why?
___________

Answer: agree

Explanation:
The ratios of the number of players in any sport to the number of players on a lacrosse team are:
{9/10, 5/10, 11/10, 6/10, 10/10, 4/10, 15/10, 11/10}
All these ratios are terminating decimals as all numerators divided by 10 lead to a terminating decimal.

Question 25.
Yvonne bought 4 \(\frac{7}{8}\) yards of material to make a dress.
a. What is 4 \(\frac{7}{8}\) written as an improper fraction?
\(\frac{□}{□}\)

Answer:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
Convert from mixed fraction to the improper fraction.
4 \(\frac{7}{8}\) = (8 × 4) + 7 = 32 + 7 = 39/8

Question 25.
b. What is 4 \(\frac{7}{8}\) written as a decimal?
______

Answer:
Remember that we need to add the whole number and just convert the fraction part to decimal.
7/8 = 0.875
The fraction is a terminating decimal. Combining the whole number and the decimal part we get,
4 + 0.875 = 4.875

Question 25.
c. Communicate Mathematical Ideas If Yvonne wanted to make 3 dresses that use 4 \(\frac{7}{8}\) yd of fabric each, explain how she could use estimation to make sure she has enough fabric for all of them.
Type below:
_____________

Answer:
Using estimation, we say that 4 \(\frac{7}{8}\) ≈ 5.
We can now multiply 3 by 5, and therefore, she needs 15 yards of fabric.

Rational Numbers and Decimals – Page No. 66

Question 26.
Vocabulary A rational number can be written as the ratio of one _______ to another and can be represented by a repeating or ______ decimal.
Type below:
_____________

Answer: A rational number can be written as the ratio of one integer to another and can be represented by a repeating or terminating decimal.

Question 27.
Problem Solving Marcus is 5 \(\frac{7}{24}\) feet tall. Ben is 5 \(\frac{5}{16}\) feet tall. Which of the two boys is taller? Justify your answer.
_____________

Answer:
Explanation:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
To determine who is taller, we convert both to decimals. Remember that we need to add the whole number and just convert the fraction part to decimal.
For Marcus:
7/24 = 0.29166..
Combine the whole number and the decimal part we get 5.29166..
For Ben:
5/16 = 0.3125
Combine the whole number and the decimal part we get 5.1325
Hence Ben is taller.

Question 28.
Represent Real-World Problems If one store is selling \(\frac{3}{4}\) of a bushel of apples for 9 dollars, and another store is selling \(\frac{2}{3}\) of a bushel of apples for 9 dollars, which store has the better deal? Explain your answer.
_____________

Answer:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
To determine which store has a better deal, we convert both fractions to decimals.
For the first store:
3/4 = 0.75
For the second store:
2/3 = 0.666..
Since the first store offers 0.75 of a bushel of apples, this store has a better deal.

Question 29.
Analyze Relationships You are given a fraction in simplest form. The numerator is not zero. When you write the fraction as a decimal, it is a repeating decimal. Which numbers from 1 to 10 could be the denominator?
Type below:
_____________

Answer: {3, 6, 7, 9}

Explanation:
Since the only numbers which can be factors of the denominators lead to a terminating decimal are 1, 2, and 5 and combinations of them, it means that if the denominator has at least one of the other numbers at the denominator, the decimal form will be a repeating decimal.
Among the numbers from 1 to 10, the presence of any of these numbers in the denominator will lead to a repeating decimal:
{3, 6, 7, 9}

Question 30.
Communicate Mathematical Ideas Julie got 21 of the 23 questions on her math test correct. She got 29 of the 32 questions on her science test correct. On which test did she get a higher score? Can you compare the fractions \(\frac{21}{23}\) and \(\frac{29}{32}\) by comparing 29 and 21? Explain. How can Julie compare her scores?
_____________

Answer:
To convert fraction decimals, we have to divide the numerator to the denominator. If the quotient goes on and on, then it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
For the math test:
21/23 = 0.9130
For the science test:
29/32 = 0.9063
Therefore she got a higher score in her math test.
Julie got a higher score in her math test. We cannot compare the fractions by comparing the numerators. Instead, we can compare her scores if the denominators of the fractions are the same.

Question 31.
Look for a Pattern Look at the decimal 0.121122111222.… If the pattern continues, is this a repeating decimal? Explain.
_____________

Answer: The number is not a repeating decimal.

Adding Rational Numbers – Guided Practice – Page No. 72

Use a number line to find each sum.

Question 1.
−3 + (−1.5) =
______

Answer: -4.5

Explanation:
Remember if the number being added is positive, move the number of units going to the right and if the number being added is negative, move the number of units to the left.
Since we are adding a negative number, starting from -3, we move 1.5 units to the left. This results in -4.5.

Question 2.
1.5 + 3.5 =
______

Answer: 5

Explanation:
Remember if the number being added is positive, move the number of units going to the right and if the number being added is negative, move the number of units to the left.
Since we are adding a positive number, starting from 1.5 we move 3.5 units to the right. This results in 5.

Question 3.
\(\frac{1}{4}+\frac{1}{2}\) =
\(\frac{□}{□}\)

Answer: \(\frac{3}{4}\)

Explanation:
Remember if the number being added is positive, move the number of units going to the right and if the number being added is negative, move the number of units to the left.
Since we are adding a positive number, starting from 1/4, we move 1/2 or 2/4, units to the right. This results in 3/4.

Question 4.
−1 \(\frac{1}{2}\) + (−1 \(\frac{1}{2}\)) =
______

Answer: -3

Explanation:
Remember if the number being added is positive, move the number of units going to the right and if the number being added is negative, move the number of units to the left.
Since we are adding a negative number, starting from −1 \(\frac{1}{2}\), we move 1 1/2 units to the left. This is results in -3.

Question 5.
3 + (−5) =
______

Answer: -2

Explanation:
Remember if the number being added is positive, move the number of units going to the right and if the number being added is negative, move the number of units to the left.
Since we are adding a negative number, starting from 3 we move 5 units to the left. This results in -2.

Question 6.
(−1.5) + 4 =
______

Answer: 2.5

Explanation:
Remember if the number being added is positive, move the number of units going to the right and if the number being added is negative, move the number of units to the left.
Since we are adding a positive number, starting from 1.5 we move 4 units to the left. This results in 2.5

Question 7.
Victor borrowed 21.50 dollars from his mother to go to the theater. A week later, he paid her 21.50 dollars back. How much does he still owe her?
______

Answer: 0

Explanation:
We use positive numbers for the money he receives and negative numbers for the money he returns.
21.50 – 21.50 = 0
The result is zero. This means he doesn’t owe anything to his mother.

Question 8.
Sandra used her debit card to buy lunch for 8.74 on Monday. On Tuesday, she deposited 8.74 back into her account. What is the overall increase or decrease in her bank account?
______

Answer: 0

Explanation:
We use positive numbers for the money she deposits and negative numbers for the money she spends.
-8.74 + 8.74 = 0
The result is zero. This means her bank account didn’t increase or decrease.

Find each sum without using a number line.

Question 9.
2.75 + (−2) + (−5.25) =
______

Answer: -4.50

Explanation:
We are given the expression:
2.75 + (-2) + (-5.25)
We group numbers with the same sign using the associative property.
2.75 – 7.25 = -4.50

Question 10.
−3 + (1 \(\frac{1}{2}\)) + (2 \(\frac{1}{2}\)) =
______

Answer: 1

Explanation:
We are given the expression
-3 + (1 \(\frac{1}{2}\)) + (2 \(\frac{1}{2}\))
-3 + 1.5 + 2.5
We group numbers with the same sign using the associative property.
-3 + 4 = 1
The larger number is having a positive sign so the sum is 1.

Question 11.
−12.4 + 9.2 + 1 =
______

Answer: -2.2

Explanation:
We are given the expression
-12.4 + 9.2 + 1
We group numbers with the same sign using the associative property.
-12.4 + 10.2 = -2.2
The larger number is having a negative sign so the answer is -2.2.

Question 12.
−12 + 8 + 13 =
______

Answer: 9

Explanation:
We are given the expression|
-12 + 8 + 13
We group numbers with the same sign using the associative property.
-12 + 21 = 9
The larger number is having the positive sign so the answer is 9.

Question 13.
4.5 + (−12) + (−4.5) =
______

Answer: -12

Explanation:
We are given the expression
4.5 + (-12) + (-4.5)
We group numbers with the same sign using the associative property.
0 – 12 = -12
The larger number is having the negative sign so the answer is -12.

Question 14.
\(\frac{1}{4}\) + (− \(\frac{3}{4}\)) =
– \(\frac{□}{□}\)

Answer: -0.50

Explanation:
We are given the expression
\(\frac{1}{4}\) + (− \(\frac{3}{4}\))
Convert the fraction to Decimal.
0.25 – 0.75 = -0.50
The larger number is having the negative sign so the sum is -0.50

Question 15.
−4 \(\frac{1}{2}\) + 2 =
– \(\frac{□}{□}\)

Answer: -2.5

Explanation:
We  = are given the expression
−4 \(\frac{1}{2}\) + 2
Convert from fraction to decimal.
-4.5 + 2 = -2.5
The larger number is having the negative sign so the sum is -2.5.

Question 16.
−8 + (−1 \(\frac{1}{8}\)) =
– \(\frac{□}{□}\)

Answer: -9.125

Explanation:
We are given the expression
−8 + (−1 \(\frac{1}{8}\))
Convert from fraction to decimal.
-8 + (-1.125) = – 9.125

Question 17.
How can you use a number line to find the sum of -4 and 6?
Type below:
____________

Answer: 6

Explanation:
Remember if the number being added is positive, move the number of units going to the right and if the number being added is negative, move the number of units to the left.
Since we are adding a positive number, starting from -4 we move 6 units to the right. This results in 2.

Adding Rational Numbers – Independent Practice – Page No. 73

Question 18.
Samuel walks forward 19 steps. He represents this movement with a positive 19. How would he represent the opposite of this number?
_______

Answer: -19
He would represent the opposite of 19 by a negative 19.

Question 19.
Julia spends 2.25 on gas for her lawn mower. She earns 15.00 mowing her neighbor’s yard. What is Julia’s profit?
_______

Answer: $12.75

Explanation:
We use positive numbers for the money she earns and negative numbers for the money she spends.
-2.25 + 15 = 12.75
Thus her profit is $12.75

Question 20.
A submarine submerged at a depth of -35.25 meters dives an additional 8.5 meters. What is the new depth of the submarine?
_______

Answer: In adding two integers with same sign add their absolute value and keep the common sign.
When adding two integers with opposite sign subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
Since the submarine dove 32.25 meters down this can be interrupted as -32.25. And because it dove an additional 8.5 meters down, we can add -8.5 meters to the previous distance.
Add 32.25 and 8.5 meters
32.25 + 8.5 = 43.75 meters
Thus the submarines new depth is 43.75 meters deep or -43.75 meters.

Question 21.
Renee hiked for 4 \(\frac{3}{4}\) miles. After resting, Renee hiked back along the same route for 3 \(\frac{1}{4}\) miles. How many more miles does Renee need to hike to return to the place where she started?
_______ \(\frac{□}{□}\)

Answer:
Given that
Renee hiked for 4 \(\frac{3}{4}\) miles. After resting, Renee hiked back along the same route for 3 \(\frac{1}{4}\) miles.
4 \(\frac{3}{4}\) + (-3 \(\frac{1}{4}\)) = 1 \(\frac{1}{2}\)
Thus Renee needs to hike to return to the place where she started is 1 \(\frac{1}{2}\) or 1.5 miles.

Question 22.
Geography
The average elevation of the city of New Orleans, Louisiana, is 0.5 m below sea level. The highest point in Louisiana is Driskill Mountain at about 163.5 m higher than New Orleans. How high is Driskill Mountain?
_______

Answer: 163 meters

Explanation:
We use the positive numbers for the elevation above the sea level and negative numbers for the elevation below the sea level.
163.5 – 0.5 = 163 meters
Thus the height of the Driskill mountain is 163 meters.

Question 23.
Problem Solving
A contestant on a game show has 30 points. She answers a question correctly to win 15 points. Then she answers a question incorrectly and loses 25 points. What is the contestant’s final score?
_______

Answer: 20

Explanation:
We use positive numbers for won points and negative numbers for lost points.
30 + 15 + (-25) = 20
Thus the final score is 20.

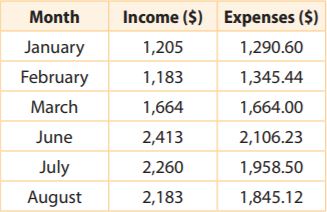
Financial Literacy

Use the table for 24–26. Kameh owns a bakery. He recorded the bakery income and expenses in a table.

Question 24.
In which months were the expenses greater than the income? Name the month and find how much money was lost.
Type below:
___________

Answer:
We count the balance for January
1205 + (-1290.60)  = -85.60
We count the balance for February
1183 + (-1345.44) = -162.44
January: $85.60
February: $162.44

Question 25.
In which months was the income greater than the expenses? Name the months and find how much money was gained.
Type below:
___________

Answer:
The income was greater than the expenses in the months:
We count the balance for june:
2413 + (-2106.23) = 306.77
We count the balance for july:
2260 + (-1958.50) = 301.5
We count the balance for august:
2183 + (-1845.12) = 337.88
June: $306.77 gained
July: $301.5 gained
August: $337.88 gained

Question 26.
Communicate Mathematical Ideas
If the bakery started with an extra $250 from the profits in December, describe how to use the information in the table to figure out the profit or loss of money at the bakery by the end of August. Then calculate the profit or loss.
Balance: $ _______

Answer: 948.71

Explanation:
If the bakery started with an extra $250 from the profits in December.
We will add this amount to January’s income.
250 + 1205 + 1183 + 1664 + 2413 + 2260 + 2183 = 11,158
We compute the expenses during the 6 months
(-1290) + (-1345.44) + (-1664) + (-2106.24) + (-1958.50) + (-1845.12) = -10209.29
11158 -10209.29 = 948.71
Since the result is a positive number, the bakery has profit.

Adding Rational Numbers – Independent Practice – Page No. 74

Question 27.
Vocabulary
-2 is the ________ of 2.
__________

Answer: additive inverse

Explanation:
When the sum of two numbers with opposite signs is 0, then they are additive inverses of eacj other.
Therefore, -2 is the additive inverse of 2.

Question 28.
The basketball coach made up a game to play where each player takes 10 shots at the basket. For every basket made, the player gains 10 points. For every basket missed, the player loses 15 points.
a. The player with the highest score sank 7 baskets and missed 3. What was the highest score?
_______ points

Answer: 25

Explanation:
We use the positive numbers for won points and negative numbers for lost points.
We determine the highest score:
7(10) + 3(-15) = 70 + (-45) = 25

Question 28.
b. The player with the lowest score sank 2 baskets and missed 8. What was the lowest score?
_______ points

Answer: -100

Explanation:
We determine the lowest score:
2(10) + 8(-15) = 20 + (-120) = -100

Question 28.
c. Write an expression using addition to find out what the score would be if a player sank 5 baskets and missed 5 baskets.
Type below:
__________

Answer: -25

Explanation:
We determine the score for 5 baskets and 5 missed baskets:
5(10) + 5(-15) = 50 + (-75)
50 – 75 = -25

H.O.T

FOCUS ON HIGHER ORDER THINKING

Question 29.
Communicate Mathematical Ideas
Explain the different ways it is possible to add two rational numbers and get a negative number.
Type below:
__________

Answer:
The sum of two rational numbers is negative either if both numbers are negative, or they have different signs, but the negative number is the one with the greater absolute value.

Question 30.
Explain the Error
A student evaluated -4 + x for x = -9 \(\frac{1}{2}\) and got an answer of 5 \(\frac{1}{2}\). What might the student have done wrong?
Type below:
__________

Answer:
We expect about 95% of all possible samples to have a 95% confidence interval that contains the population proportion who favor such an amendment.

Question 31.
Draw Conclusions
Can you find the sum [5.5 + (-2.3)] + (-5.5 + 2.3) without performing any additions?
_______

Answer:
Yes, we can find the sum without performing any computation if we notice that the two numbers from each set of brackets are the opposites of the numbers in the other set  of bracelets, thus the sum is zero:
[5.5 + (-2.3)] + (-5.5 + 2.3)
5.5 – 2.3 – 5.5 + 2.3 = 0

Subtracting Rational Numbers – Guided Practice – Page No. 79

Use a number line to find each difference.

Question 1.
5 − (−8) =
_______

Answer: 13

Explanation:
Remember if the number being subtracted is positive, move the number of units going to the left and if the number being subtracted is negative, move the number of units to the right.
Since we are subtracting a negative number, starting from 5, we move 8 units to the right. This results in 13.

Question 2.
−3 \(\frac{1}{2}\) − 4 \(\frac{1}{2}\) =
_______

Answer: -8

Explanation:
Remember if the number being subtracted is positive, move the number of units going to the left and if the number being subtracted is negative, move the number of units to the right.
Since we are subtracting a positive number, starting from −3 \(\frac{1}{2}\), we move 4 \(\frac{1}{2}\) units to the left. This results in -8.

Question 3.
−7 − 4 =
_______

Answer: -11

Explanation:
Remember if the number being subtracted is positive, move the number of units going to the left and if the number being subtracted is negative, move the number of units to the right.
Since we are subtracting a positive number, starting from -7, we move 4 units to the left. This results in -11.

Question 4.
−0.5 − 3.5 =
_______

Answer: -4

Explanation:
Remember if the number being subtracted is positive, move the number of units going to the left and if the number being subtracted is negative, move the number of units to the right.
Since we are subtracting a positive number, starting from -0.5, we move 3.5 units to the left. This results in -4

Find each difference.

Question 5.
−14 − 22 =
_______

Answer: -36

Explanation:
We have to determine the difference
-14 – 22 = (-14) + (-22) = -36
−14 − 22 = -36

Question 6.
−12.5 − (−4.8) =
_______

Answer: -7.7

Explanation:
-12.5 – (-4.8)
We convert subtraction into addition with the opposite number
-12.5 – (-4.8) = -12.5 + 4.8 = -7.7
So, the answer is -7.7

Question 7.
\(\frac{1}{3}\) − (−\(\frac{2}{3}\)) =
_______

Answer: 1

Explanation:
\(\frac{1}{3}\) − (−\(\frac{2}{3}\))
\(\frac{1}{3}\) + \(\frac{2}{3}\) = \(\frac{3}{3}\) = 1
The result is 1.

Question 8.
65 − (−14) =
_______

Answer: 79

Explanation:
We convert subtraction into addition with the opposite number
65 − (−14) = 65 + 14 = 79
The answer is 79.

Question 9.
− \(\frac{2}{9}\) − (−3) =
_______ \(\frac{□}{□}\)

Answer: 2 \(\frac{7}{9}\)

Explanation:
We convert subtraction into addition with the opposite number
− \(\frac{2}{9}\) − (−3) = − \(\frac{2}{9}\) + 3 = 2 \(\frac{7}{9}\)
The answer is 2 \(\frac{7}{9}\)

Question 10.
24 \(\frac{3}{8}\) − (−54 \(\frac{1}{8}\)) =
_______ \(\frac{□}{□}\)

Answer: 78 \(\frac{1}{2}\)

Explanation:
We convert subtraction into addition with the opposite number.
24 \(\frac{3}{8}\) − (−54 \(\frac{1}{8}\)) = 24 \(\frac{3}{8}\) + 54 \(\frac{1}{8}\) = 78 \(\frac{1}{2}\)
Thus the result is 78 \(\frac{1}{2}\).

Question 11.
A girl is snorkeling 1 meter below sea level and then dives down another 0.5 meter. How far below sea level is the girl?
_______

Answer: 1.5 meter

Explanation:
1 m below sea level is represented by the number -14. Since she is diving down 0.5 m, you must subtract -1 – 0.5 = -1.5 m
Thus the girl is 1.5 m long.

Question 12.
The first play of a football game resulted in a loss of 12 \(\frac{1}{2}\) yards. Then a penalty resulted in another loss of 5 yards. What is the total loss or gain?
_______

Answer: 17 \(\frac{1}{2}\) yards

Explanation:
The first play of a football game resulted in a loss of 12 \(\frac{1}{2}\) yards. Then a penalty resulted in another loss of 5 yards.
-12 \(\frac{1}{2}\) – 5 = -17 \(\frac{1}{2}\) yards
It is a loss of 17 \(\frac{1}{2}\) yards

Question 13.
A climber starts descending from 533 feet above sea level and keeps going until she reaches 10 feet below sea level. How many feet did she descend?
_______

Answer: 543 feet

Explanation:
Given,
A climber starts descending from 533 feet above sea level and keeps going until she reaches 10 feet below sea level.
533 feet + 10 feet = 543 feet

Question 14.
Eleni withdrew 45.00 dollars from her savings account. She then used her debit card to buy groceries for 30.15 dollars. What was the total amount Eleni took out of her account?
_______

Answer: $75.15

Explanation:
Given that,
Eleni withdrew 45.00 dollars from her savings account. She then used her debit card to buy groceries for 30.15 dollars.
$45 + $30.15 = $75.15
Thus Eleni took $75.15 out of her account.

Question 15.
Mandy is trying to subtract 4 – 12, and she has asked you for help. How would you explain the process of solving the problem to Mandy, using a number line?
Type below:
____________

Answer: Start at 4 on the number line. Then move 12 places to the left since you are subtracting. This gives -8.

Subtracting Rational Numbers – Independent Practice – Page No. 80

Question 16.
Science
At the beginning of a laboratory experiment, the temperature of a substance is -12.6 °C. During the experiment, the temperature of the substance decreases 7.5 °C. What is the final temperature of the substance?
_______

Answer: -20.1°C

Explanation:
Remember if the number being subtracted is positive, move the number of units going to the left and if the number being subtracted is negative, move the number of units to the right.
Since the temperature of the substance is -12.6 and it decreases further by 7.5, we can create the expression -12.6 – 7.5.
-12.6 – 7.5 = -20.1
Thus the final temperature is -20.1°C

Question 17.
A diver went 25.65 feet below the surface of the ocean, and then 16.5 feet further down, he then rose 12.45 feet. Write and solve an expression to find the diver’s new depth.
_______

Answer: -29.7 feet

Explanation:
Remember if the number being subtracted is positive, move the number of units going to the left and if the number being subtracted is negative, move the number of units to the right.
Since the diver went down 25.65 feet then dove again further by 16.5 feet then rose up by 12.45 feet, we can create the expression -25.65 – 16.5 + 12.45 = -29.7 feet
The diver’s new depth is -29.7 feet.

Question 18.
A city known for its temperature extremes started the day at -5 degrees Fahrenheit. The temperature increased by 78 degrees Fahrenheit by midday, and then dropped 32 degrees by nightfall.
a. What expression can you write to find the temperature at nightfall?
Type below:
____________

Answer:
The temperature started at -5 degrees then increased 78 degrees and then dropped 32 degrees.
The expression is -5 + 78 – 32

Question 18.
b. What expression can you write to describe the overall change in temperature? Hint: Do not include the temperature at the beginning of the day since you only
Type below:
____________

Answer: The overall change is the increase and decrease combined.
The expression is 78 – 32

Question 18.
c. What is the final temperature at nightfall? What is the overall change in temperature?
Type below:
____________

Answer:
Use the first expression -5 + 78 – 32 = 73 – 32 = 41 degrees
78 – 32 = 46 degrees

Question 19.
Financial Literacy
On Monday, your bank account balance was -$12.58. Because you didn’t realize this, you wrote a check for $30.72 for groceries.
a. What is the new balance in your checking account?
$ _______

Answer:
Subtract the check amount from the initial balance.
-$12.58 – $30.72 = -$43.30

Question 19.
b. The bank charges a $25 fee for paying a check on a negative balance. What is the balance in your checking account after this fee?
$ _______

Answer:
Subtract 25 from the balance from part a.
-$43.30 – $25 = -$68.30

Question 19.
c. How much money do you need to deposit to bring your account balance back up to $0 after the fee?
$ _______

Answer:
Since the account balance is -$68.30, a deposit of $68.30 is required to make the balance $0.

Astronomy

Use the table for problems 20–21.

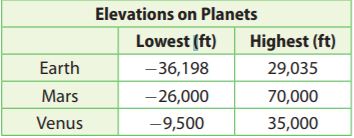
Question 20.
How much deeper is the deepest canyon on Mars than the deepest canyon on Venus?
_______

Answer: -16,500 feet deper

Explanation:
Subtract the lowest elevations of Mars and Venus.
-26,000 – (-9500) = -16,500

Question 21.
Persevere in Problem Solving
What is the difference between Earth’s highest mountain and its deepest ocean canyon? What is the difference between Mars’ highest mountain and its deepest canyon? Which difference is greater? How much greater is it?
Type below:
____________

Answer:
Subtract the highest elevation and the lowest elevation on Earth.
29,035 – (-36,198) = 65,233
Subtract the highest elevation and the lowest elevation on Mars.
96,000 – 65,233 = 30,767
96,000 is greater than 65,233 so the difference for Mars is greater. subtract these two numbers to get how much greater.

Subtracting Rational Numbers – Page No. 81

Question 22.
Pamela wants to make some friendship bracelets for her friends. Each friendship bracelet needs 5.2 inches of string.
a. If Pamela has 20 inches of string, does she have enough to make bracelets for 4 of her friends?
a. _______

Answer: no

Explanation:
Each bracelet needs 5.2 inches so multiply 4 and 5.2 inches to see how many total inches she needs this is greater than 20 so she does not have enough.
4 × 5.2 = 20.8 inches

Question 22.
b. If so, how much string would she had left over? If not, how much more string would she need?
_______ in.

Answer: She needs 0.8 inches more

Question 23.
Jeremy is practicing some tricks on his skateboard. One trick takes him forward 5 feet, then he flips around and moves backwards 7.2 feet, then he moves forward again for 2.2 feet.
a. What expression could be used to find how far Jeremy is from his starting position when he finishes the trick?
Type below:
___________

Answer: 5 – 7.2 + 2.2

Explanation:
He moves 5 feet forward, back 7.2 feet, and then forward 2.2 feet.

Question 23.
b. How far from his starting point is he when he finishes the trick? Explain
_______ ft.

Answer: 0 ft

Explanation:
Since the distance just pulls hi back and forth at the same amount of distance.
5 – 7.2 + 2.2 = 0 ft

Question 24.
Esteban has $20 from his allowance. There is a comic book he wishes to buy that costs $4.25, a cereal bar that costs $0.89, and a small remote control car that costs $10.99.
a. Does Esteban have enough to buy everything?
a. _______

Answer:
Find the total amount of money he wants to spend this is less than 20 so he has enough
4.25 + 0.89 + 10.99 = 16.13
Thus Esteban had enough money.

Question 24.
b. If so, how much will he have left over? If not, how much does he still need?
$ _______

Answer:
Subtract the amount he wants to spend from the amount he has to find how much he has left.
20 – 16.13 = 3.87
Thus $3.87 left.

Subtracting Rational Numbers – H.O.T – Page No. 82

Focus on Higher Order Thinking

Question 25.
Look for a Pattern
Show how you could use the Commutative Property to simplify the evaluation of the expression \(-\frac{7}{16}-\frac{1}{4}-\frac{5}{16}\).
_______

Answer:
\(-\frac{7}{16}-\frac{1}{4}-\frac{5}{16}\)
-12/16 – 1/4
= -3/4 -1/4
= -4/4 = -1

Question 26.
Problem Solving
The temperatures for five days in Kaktovik, Alaska, are given below.
-19.6 °F, -22.5 °F, -20.9 °F, -19.5 °F, -22.4 °F
Temperatures for the following week are expected to be twelve degrees lower every day. What are the highest and lowest temperatures expected for the corresponding 5 days next week?
Type below:
____________

Answer:
The highest temperature for the first five days was -19.5 degrees so the highest temperature the following week is 12 degrees less than that. the lowest temperature the first week was -22.9 degree so the lowest temperature the second week is 12 degree below that
high: -19.5 – 12 = -31.5°F
low: -22.5 – 12 = -34.5°F

Question 27.
Make a Conjecture
Must the difference between two rational numbers be a rational number? Explain.
_______

Answer:
Yes, the difference between two rational numbers must be rational. Subtracting two fractions equals a fraction of an integer. Integers are rational numbers so even if the answer isn’t a fraction, it is still a rational number.

Question 28.
Look for a Pattern
Evan said that the difference between two negative numbers must be negative. Was he right? Use examples to illustrate your answer.
_______

Answer:
He is not correct. The difference between -2 and -5 is -2- (-5) = -2 + 5 = 3
which is not negative.

Multiply Rational Numbers – Guided Practice – Page No. 86

Use a number line to find each product.

Question 1.
5(−\(\frac{2}{3}\)) =
_______ \(\frac{□}{□}\)

Answer: -3 \(\frac{1}{3}\)

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying −\(\frac{2}{3}\) by 5, starting from 0, we move \(\frac{2}{3}\) units to the left five times. This results in -3 \(\frac{1}{3}\)

Question 2.
3(−\(\frac{1}{4}\)) =
\(\frac{□}{□}\)

Answer: –\(\frac{3}{4}\)

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying −\(\frac{1}{4}\) by 3, starting from 0, we move −\(\frac{1}{4}\) units to the left three times. This results in –\(\frac{3}{4}\).

Question 3.
−3(−\(\frac{4}{7}\)) =
_______ \(\frac{□}{□}\)

Answer: 1 \(\frac{5}{7}\)

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying −\(\frac{4}{7}\) by -3, let us first multiply −\(\frac{4}{7}\) by 3. Starting from 0, we move \(\frac{4}{7}\) units to the left three times.
This results in -1 \(\frac{5}{7}\)
Therefore the opposite of this is 1 \(\frac{5}{7}\).

Question 4.
−\(\frac{3}{4}\)(−4) =
______

Answer: 3

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying −\(\frac{3}{4}\) by -4, let us first multiply −\(\frac{3}{4}\) by 4. Starting from 0, we move \(\frac{3}{4}\) units to the left three times. This results in -3. Therefore the opposite of this is 3.

Question 5.
4(−3) =
______

Answer: -12

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying -3 by 4, starting from 0, we move 3 units to the left four times. This results in -12.

Question 6.
(−1.8)5 =
______

Answer: -9

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying -1.8 by 5, starting from 0, we move 1.8 units to the left five times. This results in -9.

Question 7.
−2(−3.4) =
______

Answer: 6.8

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying -2 by -3.4, starting from 0, starting from 0, we move 3.4 units to the left two times. This results in -6.8. Therefore, the opposite of this is 6.8.

Question 8.
0.54(8) =
______

Answer: 4.32

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying 0.54 by 8, starting from 0, we move 0.54 units to the right eight times. This results in 4.32.

Question 9.
−5(−1.2) =
______

Answer: 6

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying -1.2 by -5, Starting from 0, we move 1.2 units to the left five times. This results in -6. Therefore the opposite of this is 6.

Question 10.
−2.4(3) =
______

Answer: -7.2

Explanation:
Remember if the number being multiplied is positive, starting from zero move the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Since we are multiplying -2.4 by 3, starting from 0, we move 2.4 units to the left three times. This results in -7.2

Multiply.

Question 11.
\(\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4}\) = □ × \(\frac{3}{4}\) =
\(\frac{□}{□}\)

Answer: \(\frac{1}{4}\)

Explanation:
\(\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4}\) = □ × \(\frac{3}{4}\)
1/3 × 3/4 = 1/4
\(\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4}\) = □ × \(\frac{3}{4}\) = \(\frac{1}{4}\)

Question 12.
\(-\frac{4}{7}\left(-\frac{3}{5}\right)\left(-\frac{7}{3}\right)\) = □ × \(\left(-\frac{7}{3}\right)\) =
\(\frac{□}{□}\)

Answer: – \(\frac{4}{5}\)

Explanation:
Multiply the first two fractions by multiplying the top numbers together and multiply the bottom numbers together.
Remember that two negatives make a positive so the product of the first two fractions is positive.
\(-\frac{4}{7}\left(-\frac{3}{5}\right)\left(-\frac{7}{3}\right)\) = □ × \(\left(-\frac{7}{3}\right)\)
12/35 × -7/3 = -4/5

Question 13.
\(-\frac{1}{8} \times 5 \times \frac{2}{3}\) =
\(\frac{□}{□}\)

Answer: –\(\frac{5}{12}\)

Explanation:
Use the commutative property to switch the order of the first two fractions.
\(-\frac{1}{8} \times 5 \times \frac{2}{3}\) = –\(\frac{1}{8}\) × \(\frac{2}{3}\) × 5
–\(\frac{1}{12}\) × 5 = –\(\frac{5}{12}\)

Question 14.
\(-\frac{2}{3}\left(\frac{1}{2}\right)\left(-\frac{6}{7}\right)\) =
\(\frac{□}{□}\)

Answer: \(\frac{2}{7}\)

Explanation:
Multiply the first two fractions by cancelling the 2s.
\(-\frac{2}{3}\left(\frac{1}{2}\right)\left(-\frac{6}{7}\right)\) = –\(\frac{1}{3}\)(-\(\frac{6}{7}\))
Multiply by cancelling the 3 and 6 to get a 2 in the numerator two negatives make a positive.
So the answer is \(\frac{2}{7}\)

Question 15.
The price of one share of Acme Company declined $3.50 per day for 4 days in a row. What is the overall change in price of one share?
$ _______

Answer: -$14

Explanation:
Given that,
The price of one share of Acme Company declined $3.50 per day for 4 days in a row.
-$3.50 × 4 = -$14.00
Thus the overall change in the price of one share is -$14.

Question 16.
In one day, 18 people each withdrew $100 from an ATM machine. What is the overall change in the amount of money in the ATM machine?
$ _______

Answer: The overall change in the amount of money in the ATM machine is the product of the amount people withdrew times the number of people. This gives -100(18) = -1800.
Therefore the overall change in the amount of money in the ATM machine is -$1800.

Question 17.
Explain how you can find the sign of the product of two or more rational numbers.
Type below:
____________

Answer: If the product has an even number of negative signs, then the product is positive. If the product has an odd number of negative signs, then the product is negative.

Multiply Rational Numbers – Independent Practice – Page No. 87

Question 18.
Financial Literacy
Sandy has $200 in her bank account.
a. If she writes 6 checks for exactly $19.98, what expression describes the change in her bank account?
_______

Answer: The change in her bank account is equal to the product of the check amounts and the number of checks.
This gives the expressions 6(-19.98)

Question 18.
b. What is her account balance after the checks are cashed?
$ _______

Answer: She started with $200 and her account balance changes by 6(-19.98) dollars so her account balance is 200 – 6(-19.98) = 200 – 119.88 = 80.12

Question 19.
Communicating Mathematical Ideas
Explain, in words, how to find the product of -4(-1.5) using a number line. Where do you end up?
Type below:
____________

Answer:
First, find the value of -4(-1.5) by starting at 0 on the number line and moving 1.5 units left four times.
This gives a value of 4(-1.5) = -6
Since -4(-1.5) is the opposite of 4(-1.5), the answer is 6.

Question 20.
Greg sets his watch for the correct time on Wednesday. Exactly one week later, he finds that his watch has lost 3 \(\frac{1}{4}\) minutes. If his watch continues to lose time at the same rate, what will be the overall change in time after 8 weeks?
_______ minutes

Answer: 26 minutes

Explanation:
Given,
Greg sets his watch for the correct time on Wednesday.
Exactly one week later, he finds that his watch has lost 3 \(\frac{1}{4}\) minutes.
8(3 \(\frac{1}{4}\)) = 8 \(\frac{13}{4}\)
= 2 × 13 = 26 minutes.
Therefore the overall change in time after 8 weeks is 26 minutes.

Question 21.
A submarine dives below the surface, heading downward in three moves. If each move downward was 325 feet, where is the submarine after it is finished diving?
_______ feet

Answer: 975

Explanation:
Moving downward is represented by a negative number. Multiply the distance traveled down by the number of moves.
3 × -325 feet = -975
The submarine is 975 feet below the surface.

Question 22.
Multistep
For Home Economics class, Sandra has 5 cups of flour. She made 3 batches of cookies that each used 1.5 cups of flour. Write and solve an expression to find the amount of flour Sandra has left after making the 3 batches of cookies.
_______ cups

Answer: 0.5 cups

Explanation:
Sandra has a total of 5 cups of flour. Since she used 1.5 cups per batch of the cookie, and there are 3 batches, we can subtract the product of the cups and the number of batches
1.5 × 3 = 4.5
Therefore the expression should be 5 – 4.5 = 0.5
Thus Sandra has 0.5 cups of flour left.

Question 23.
Critique Reasoning
In class, Matthew stated,“I think that a negative is like the opposite. That is why multiplying a negative times a negative equals a positive. The opposite of negative is positive, so it is just like multiplying the opposite of a negative twice, which is two positives.”
Do you agree or disagree with his reasoning? What would you say in response to him?
_______

Answer: I agree with him. The product of two negatives is positive because the product of two positives is positive and negatives are opposites of positives.

Question 24.
Kaitlin is on a long car trip. Every time she stops to buy gas, she loses 15 minutes of travel time. If she has to stop 5 times, how late will she be getting to her destination?
_______ minutes

Answer: 75 minutes

Explanation:
Multiply the number of stops by the length of each stop to find the time she will be late.
5 × 15 = 75
Thus Kaitlin will be 75 minutes late to reach her destination.

Multiply Rational Numbers – Page No. 88

Question 25.
The table shows the scoring system for quarterbacks in Jeremy’s fantasy football league. In one game, Jeremy’s quarterback had 2 touchdown passes, 16 complete passes, 7 incomplete passes, and 2 interceptions. How many total points did Jeremy’s quarterback score?

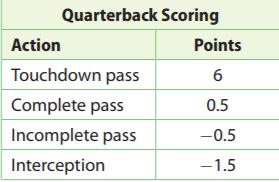
_______ pts

Answer: 13.5 points

Explanation:
Write the expression for the total number of points
2(6) + 16(0.5) + 7(-0.5) + 2(-1.5)
= 12 + 8 – 3.5 – 3
= 20 – 6.5
= 13.5
Thus Jeremy’s quarterback scored 13.5 points.

H.O.T

Focus On Higher Order Thinking

Question 26.
Represent Real-World Problems
The ground temperature at Brigham Airport is 12 °C. The temperature decreases by 6.8 °C for every increase of 1 kilometer above the ground. What is the overall change in temperature outside a plane flying at an altitude of 5 kilometers above Brigham Airport?
_______ °C

Answer: -22°C

Explanation:
Remember if the number being multiplied is positive, starting from zero moves the number of units by how many times it is multiplied going to the right and if the number being multiplied is negative, starting from zero, move the number of units by how many times it is multiplied going to the left.
Note that the ground temperature is 12°C. Since the temperature decreases by 6.8°C for every kilometer above ground, and the given height of the plane is 5 kilometers,
We can subtract the product of the temperature and the distance 5(6.8) from the ground temperature.
Therefore the expression should be 12 – 5(6.8)
= 12 – 34
= -22
Thus the temperature outside a plane flying at an altitude of 5 kilometers above Brigham Airport is -22°C

Question 27.
Identify Patterns
The product of four numbers, a, b, c, and d, is a negative number. The table shows one combination of positive and negative signs of the four numbers that could produce a negative product. Complete the table to show the seven other possible combinations.

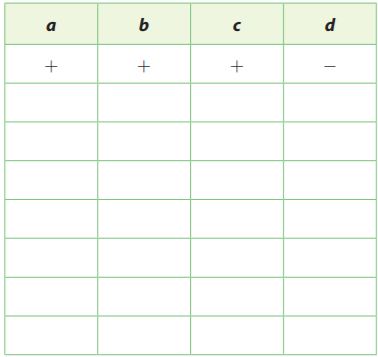
Type below:
_____________

Answer:
In multiplying numbers, an odd number of negative signs produces a negative product.

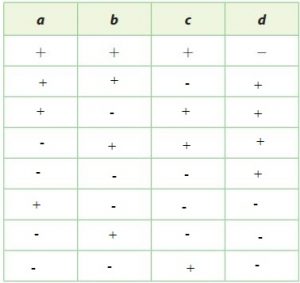
Question 28.
Reason Abstractly
Find two integers whose sum is -7 and whose product is 12. Explain how you found the numbers.
Type below:
_____________

Answer: -3 and -4

Explanation:
Let x and y be the two numbers. Write the equations using the given information
x + y = -7
xy = 12
Since the two numbers multiply to a positive and add to a negative the two numbers must be negative. Find the pairs of negative numbers that multiply to 12.
-1 and -12, -2 and -6 and -3 and -4.
Thus the pairs that have a sum as -7 and product as 12 is -3 and -4.

Divide Rational Numbers – Guided Practice – Page No. 92

Find each quotient.

Question 1.
\(\frac{0.72}{-0.9}\) =
_______

Answer: -0.8

Explanation:
We have to find the quotient:
\(\frac{0.72}{-0.9}\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
\(\frac{0.72}{-0.9}\) = -0.8

Question 2.
\(\left(-\frac{\frac{1}{5}}{\frac{7}{5}}\right)\) =
\(\frac{□}{□}\)

Answer: – \(\frac{1}{7}\)

Explanation:
We have to find the quotient:
\(\left(-\frac{\frac{1}{5}}{\frac{7}{5}}\right)\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
\(\left(-\frac{\frac{1}{5}}{\frac{7}{5}}\right)\) = – \(\frac{5}{35}\) = – \(\frac{1}{7}\)

Question 3.
\(\frac{56}{-7}\) =
_______

Answer: -8

Explanation:
We have to find the quotient:
\(\frac{56}{-7}\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
7 divides 56 eight times.
Thus the quotient of \(\frac{56}{-7}\) = -8

Question 4.
\(\frac{251}{4} \div\left(-\frac{3}{8}\right)\) =
\(\frac{□}{□}\)

Answer: –\(\frac{502}{3}\)

Explanation:
We have to find the quotient:
\(\frac{251}{4} \div\left(-\frac{3}{8}\right)\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
Rewrite using multiplication by multiplying with the reciprocal.
\(\frac{251}{4}\) × –\( \frac{8}{3}\) = –\(\frac{2008}{12}\)
–\(\frac{2008}{12}\) = –\(\frac{502}{3}\)
The quotient of \(\frac{251}{4} \div\left(-\frac{3}{8}\right)\) is –\(\frac{502}{3}\)

Question 5.
\(\frac{75}{-\frac{1}{5}}\) =
_______

Answer: -375

Explanation:
We have to find the quotient:
\(\frac{75}{-\frac{1}{5}}\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
75 ÷ 1/5
75 × -5 = -375
Thus the quotient of \(\frac{75}{-\frac{1}{5}}\) is -375.

Question 6.
\(\frac{-91}{-13}\) =
_______

Answer: 7

Explanation:
We have to find the quotient:
\(\frac{-91}{-13}\)
We determine the sign of the quotient.
The quotient will be positive because the numbers have the same signs.
13 divides 91 seven times.
\(\frac{-91}{-13}\) = 7
Thus the quotient is 7.

Question 7.
\(\frac{-\frac{3}{7}}{\frac{9}{4}}\) =
\(\frac{□}{□}\)

Answer: –\(\frac{4}{21}\)

Explanation:
We have to find the quotient:
\(\frac{-\frac{3}{7}}{\frac{9}{4}}\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
\(\frac{-\frac{3}{7}}{\frac{9}{4}}\) = -3/7 × 4/9 = -12/63
-12/63 = -4/21
\(\frac{-\frac{3}{7}}{\frac{9}{4}}\) = –\(\frac{4}{21}\)

Question 8.
– \(\frac{12}{0.03}\) =
_______

Answer: -400

Explanation:
We have to find the quotient:
– \(\frac{12}{0.03}\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
– \(\frac{12}{0.03}\) = -400
So the quotient is -400.

Question 9.
A water pail in your backyard has a small hole in it. You notice that it has drained a total of 3.5 liters in 4 days. What is the average change in water volume each day?
_______ liters per day

Answer: -0.875 litres/day

Explanation:
Given that,
A water pail in your backyard has a small hole in it. You notice that it has drained a total of 3.5 liters in 4 days.
The average change of water volume each day is the quotient.
So, divide -3.5 by 4.
The quotient will be negative because the numbers have different signs.
-3.5/4 = -0.875
Thus the water volume diminishes by 0.875 liters each day.

Question 10.
The price of one share of ABC Company declined a total of $45.75 in 5 days. What was the average change of the price of one share per day?
$ _______

Answer: -$9.15

Explanation:
The price of one share of ABC Company declined a total of $45.75 in 5 days.
We use negative numbers for the price going down.
The average change in the price of one share per day is the quotient.
-45.75/5
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
-45.75/5 = -9.15
Thus the price of one share diminishes by $9.15 per day.

Question 11.
To avoid a storm, a passenger-jet pilot descended 0.44 mile in 0.8 minutes. What was the plane’s average change of altitude per minute?
_______

Answer: -0.55 miles/min

Explanation:
We use negative numbers for the altitude going down.
The plane’s average change of altitude per minute is the quotient:
-0.44/0.8
We determine the sign of the quotient
The quotient will be negative because the numbers have different signs.
-0.44/0.8 = -0.55
Therefore the plane descends by 0.55 miles per minute.

Essential Question Check-In

Question 12.
Explain how you would find the sign of the quotient \(\frac{32 \div(-2)}{-16 \div 4}\).
Type below:
___________

Answer: positive

Explanation:
Given,
\(\frac{32 \div(-2)}{-16 \div 4}\)
Since all the operations are of multiplication and division, the sign is given by the number of negative signs.
If the number of negative signs is even, the quotient is positive while if the number of negative signs is odd, the quotient is negative.
In this case, the number of negative signs is 2, therefore even, so the quotient is positive.
\(\frac{32 \div(-2)}{-16 \div 4}\) = -16/-4 = 4
Thus the solution is positive.

Divide Rational Numbers – Independent Practice – Page No. 93

Question 13.
\(\frac{5}{-\frac{2}{8}}\) =
_______

Answer: -20

Explanation:
We are given the expression:
\(\frac{5}{-\frac{2}{8}}\)
The quotient will be negative because the numbers have different signs.
\(\frac{5}{-\frac{2}{8}}\) = 5 ÷ (-2/8)
We rewrite using the multiplication by multiplying with the reciprocal:
5 × -8/2 = 5 × -4 = -20
Thus the quotient for \(\frac{5}{-\frac{2}{8}}\) is -20.

Question 14.
\(5 \frac{1}{3} \div\left(-1 \frac{1}{2}\right)\) =
\(\frac{□}{□}\)

Answer: – \(\frac{32}{9}\)

Explanation:
We have to find the quotient:
\(5 \frac{1}{3} \div\left(-1 \frac{1}{2}\right)\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
16/3 ÷ -3/2
16/3 × -2/3 = -32/9
Thus the quotient for \(5 \frac{1}{3} \div\left(-1 \frac{1}{2}\right)\) is – \(\frac{32}{9}\)

Question 15.
\(\frac{(-120)}{(-6)}\) =
_______

Answer: 20

Explanation:
We have to find the quotient:
\(\frac{(-120)}{(-6)}\)
We determine the sign of the quotient.
The quotient will be positive because the numbers have the same signs.
6 divides 120 twenty times.
\(\frac{(-120)}{(-6)}\) = 20
Thus the quotient for \(\frac{(-120)}{(-6)}\) is 20.

Question 16.
\(\frac{-\frac{4}{5}}{-\frac{2}{3}}\) =
\(\frac{□}{□}\)

Answer: \(\frac{6}{5}\)

Explanation:
We have to find the quotient:
\(\frac{-\frac{4}{5}}{-\frac{2}{3}}\)
We determine the sign of the quotient.
The quotient will be positive because the numbers have the same signs.
(-4/5) × (-3/2) = 12/10 = 6/5
Thus the quotient for \(\frac{-\frac{4}{5}}{-\frac{2}{3}}\) is \(\frac{6}{5}\)

Question 17.
1.03 ÷ (−10.3) =
_______

Answer: -0.1

Explanation:
We have to find the quotient:
1.03 ÷ (−10.3)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
1.03 ÷ (-10.3) = -0.1

Question 18.
\(\frac{(-0.4)}{80}\) =
_______

Answer: -0.005

Explanation:
We have to find the quotient:
\(\frac{(-0.4)}{80}\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
\(\frac{(-0.4)}{80}\) = -0.005
Thus the quotient for \(\frac{(-0.4)}{80}\) is -0.005.

Question 19.
\(1 \div \frac{9}{5}\) =
\(\frac{□}{□}\)

Answer: \(\frac{5}{9}\)

Explanation:
We have to find the quotient:
\(1 \div \frac{9}{5}\)
We determine the sign of the quotient.
The quotient will be positive because the numbers have the same signs
\(1 \div \frac{9}{5}\) = 1 × 5/9 = 5/9
Thus the quotient for \(1 \div \frac{9}{5}\) is \(\frac{5}{9}\)

Question 20.
\(\frac{\frac{-1}{4}}{\frac{23}{0.4}}\) =
\(\frac{□}{□}\)

Answer: –\(\frac{6}{23}\)

Explanation:
We have to find the quotient:
\(\frac{\frac{-1}{4}}{\frac{23}{0.4}}\)
We determine the sign of the quotient.
The quotient will be negative because the numbers have different signs.
\(\frac{\frac{-1}{4}}{\frac{23}{0.4}}\) = (-1/4) . (24/23) = -24/92
-24/92 = -6/23
Thus the quotient for \(\frac{\frac{-1}{4}}{\frac{23}{0.4}}\) is –\(\frac{6}{23}\)

Question 21.
\(\frac{-10.35}{-2.3}\) =
_______

Answer: 4.5

Explanation:
We have to find the quotient:
\(\frac{-10.35}{-2.3}\)
We determine the sign of the quotient.
The quotient will be positive because the numbers have the same signs
\(\frac{-10.35}{-2.3}\) = 4.5
So, the quotient for \(\frac{-10.35}{-2.3}\) is 4.5

Question 22.
Alex usually runs for 21 hours a week, training for a marathon. If he is unable to run for 3 days, describe how to find out how many hours of training time he loses, and write the appropriate integer to describe how it affects his time.
_______ hours

Answer: -9

Explanation:
Alex usually runs for 21 hours a week, training for a marathon.
If he runs 21 hours a week, he runs 21/3 = 3 hours.
If he doesn’t run for 3 days, then he is losing 3(3) = 9 hours of training time.
Since he is losing hours, the integer is negative so the answer is -9.

Question 23.
The running back for the Bulldogs football team carried the ball 9 times for a total loss of 15 \(\frac{3}{4}\) yards. Find the average change in field position on each run.
\(\frac{□}{□}\) yards per run

Answer: 1 \(\frac{3}{4}\) yards per run

Explanation:
The running back for the Bulldogs football team carried the ball 9 times for a total loss of 15 \(\frac{3}{4}\) yards
Convert from mixed fractions to the improper fraction.
15 \(\frac{3}{4}\) = \(\frac{63}{4}\)
\(\frac{63}{4}\) × \(\frac{1}{9}\)
Divide 63 and 9 by 9 and then multiply the remaining factors.
\(\frac{7}{4}\) × 1 = \(\frac{7}{4}\)
Rewrite as a mixed fraction.
\(\frac{7}{4}\) = 1 \(\frac{3}{4}\) yards per run.

Question 24.
The 6:00 a.m. temperatures for four consecutive days in the town of Lincoln were -12.1 °C, -7.8°C, -14.3°C, and -7.2°C. What was the average 6:00 a.m. temperature for the four days?
_______ °C

Answer: -10.35°C

Explanation:
The average is the sum of the temperatures divided by the number of temperatures.
(-12.1 – 7.8 – 14.3 – 7.2)/4
= 41.4/4 = -10.35°C

Question 25.
Multistep
A seafood restaurant claims an increase of $1,750.00 over its average profit during a week where it introduced a special of baked clams.
a. If this is true, how much extra profit did it receive per day?
$ _______ per day

Answer:
There are 7 days in a week so divide the total profit of $1750 by 7 to find the extra profit per day.
1750/7 = 250
Thus he receive $250 extra profit per day.

Question 25.
b. If it had, instead, lost $150 per day, how much money would it have lost for the week?
$ _______

Answer:
Multiply the daily loss of $150 by 7 to get the weekly loss.
150 × 7 = $1050

Question 25.
c. If its total loss was $490 for the week, what was its average daily change?
$ _______ per day

Answer:
Since the company lost $490, its income changed by -$490.
Divide the change in income by 7 to find the average daily change.
-$490/7 = -$70
Thus the average daily change is -$70 per day.

Question 26.
A hot air balloon descended 99.6 meters in 12 seconds. What was the balloon’s average rate of descent in meters per second?
_______ m/s

Answer: 8.3 meters per second

Explanation:
Given that,
A hot air balloon descended 99.6 meters in 12 seconds.
99.6/12 = 8.3 meters per second.
Thus the balloon’s average rate of descent is 8.3 meters per second.

Divide Rational Numbers – Page No. 94

Question 27.
Sanderson is having trouble with his assignment. His shown work is as follows:
\(\frac{-\frac{3}{4}}{\frac{4}{3}}=-\frac{3}{4} \times \frac{4}{3}=-\frac{12}{12}=-1\)
However, his answer does not match the answer that his teacher gives him. What is Sanderson’s mistake? Find the correct answer.
\(\frac{□}{□}\)

Answer: – \(\frac{9}{16}\)

Explanation:
Sanderson made the mistake of not flipping the bottom fraction when he rewrote the problem as multiplication. The correct work is
\(\frac{-\frac{3}{4}}{\frac{4}{3}}\) = -3/4 × 4/3 = – \(\frac{9}{16}\)

Question 28.
Science
Beginning in 1996, a glacier lost an average of 3.7 meters of thickness each year. Find the total change in its thickness by the end of 2012.
_______ meters

Answer: 59.2 meters

Explanation:
Beginning in 1996, a glacier lost an average of 3.7 meters of thickness each year.
1996 to 2012 is 16 years so the total change in thickness is 16(3.7) = 59.2 meters.

H.O.T

Focus On Higher Order Thinking

Question 29.
Represent Real-World Problems
Describe a real-world situation that can be represented by the quotient -85 ÷ 15. Then find the quotient and explain what the quotient means in terms of the real-world situation.
Quotient: _______

Answer: -5.67

Explanation:
A possible real-world situation could be:
Sam has withdrawn $85 from his bank account over a period of 15 days. Find the average change in his account balance per day.
Answer: -85/15 = -5.67
So, the average rate of change in his account balance is -$5.67 per day.

Question 30.
Construct an Argument
Divide 5 by 4. Is your answer a rational number? Explain.
_______

Answer: The quotient is a rational number because it is a fraction.

Question 31.
Critical Thinking
Should the quotient of an integer divided by a nonzero integer always be a rational number? Why or why not?
_______

Answer:
Remember that in dividing and simplifying rational numbers, the quotient is positive if the signs of the numbers are the same, and negative if the signs of the numbers are different.
The quotient should be a rational number. This is because since the integers can be expressed as a quotient of two integers, then it is a rational number.

Applying Rational Number Operations – Guided Practice – Page No. 98

Question 1.
Mike hiked to Big Bear Lake in 4.5 hours at an average rate of 3 \(\frac{1}{5}\) miles per hour. Pedro hiked the same distance at a rate of 3 \(\frac{3}{5}\) miles per hour. How long did it take Pedro to reach the lake?
_______ hours

Answer: 4 hours

Explanation:
Given that,
Mike hiked to Big Bear Lake in 4.5 hours at an average rate of 3 \(\frac{1}{5}\) miles per hour. Pedro hiked the same distance at a rate of 3 \(\frac{3}{5}\) miles per hour.
4.5h × 3 \(\frac{3}{5}\) miles per hour = 4.5 × 3.2 miles = 14.4 miles
Plug in the distance you found in step 1 and the given rate in the problem to find the number of hours for Pedro.
14.4 miles ÷ 3 \(\frac{3}{5}\) miles per hour = 14.4 ÷ 3.6 hours = 4 hours

Question 2.
Until this year, Greenville had averaged 25.68 inches of rainfall per year for more than a century. This year’s total rainfall showed a change of −2 \(\frac{3}{8}\)% with respect to the previous average. How much rain fell this year?
_______ inches

Answer: 25.0701 inches

Explanation:
Greenville had averaged 25.68 inches of rainfall per year for more than a century.
This year’s total rainfall showed a change of −2 \(\frac{3}{8}\)% with respect to the previous average.
−2 \(\frac{3}{8}\)% = -2.375% = -0.02375
25.68 × 0.02375 ≈ 0.6099 inches
Find this year’s total rainfall
25.68 inches – 0.6099 inches = 25.0701 inches

Essential Question Check-In

Question 3.
Why is it important to consider using tools when you are solving a problem?
Type below:
___________

Answer: It is important to consider using tools, such as a calculator, when solving problems because some problems involve multiplying and dividing decimals that are too time consuming to do by hand.

Applying Rational Number Operations – Independent Practice – Page No. 99

Solve, using appropriate tools.

Question 4.
Three rock climbers started a climb with each person carrying 7.8 kilograms of climbing equipment. A fourth climber with no equipment joined the group. The group divided the total weight of climbing equipment equally among the four climbers. How much did each climber carry?
_______ kilograms

Answer: 5.85 kilograms

Explanation:
Given,
Three rock climbers started a climb with each person carrying 7.8 kilograms of climbing equipment.
A fourth climber with no equipment joined the group.
3 × 7.8 = 23.4
The group divided the total weight of climbing equipment equally among the four climbers.
23.4/4 = 5.85 kilograms
Thus each climber carry 5.85 kilograms

Question 5.
Foster is centering a photo that is 3 \(\frac{1}{2}\) inches wide on a scrapbook page that is 12 inches wide. How far from each side of the page should he put the picture?
________ \(\frac{□}{□}\) inches

Answer: 4 \(\frac{1}{4}\) inches

Explanation:
Given,
Foster is centering a photo that is 3 \(\frac{1}{2}\) inches wide on a scrapbook page that is 12 inches wide.
Let x be how far the photo is from each side of the page.
Since the photo is 3 \(\frac{1}{2}\) inches wide, then the total width of the page is
x + 3 \(\frac{1}{2}\) + x = 2x + 3 \(\frac{1}{2}\)
2x + 3 \(\frac{1}{2}\) = 12
2x + 7/2 = 12
2x = 17/2
x = 17/4
Convert the fraction to the mixed fraction.
x = 4 \(\frac{1}{4}\) inches

Question 6.
Diane serves breakfast to two groups of children at a daycare center. One box of Oaties contains 12 cups of cereal. She needs \(\frac{1}{3}\) cup for each younger child and \(\frac{3}{4}\) cup for each older child. Today’s group includes 11 younger children and 10 older children. Is one box of Oaties enough for everyone? Explain.
________

Answer: Yes

Explanation:
11 × \(\frac{1}{3}\) + 10 × \(\frac{3}{4}\)
\(\frac{11}{3}\) + \(\frac{15}{2}\)
\(\frac{22}{6}\) + \(\frac{45}{6}\) = \(\frac{67}{6}\)
= 11 \(\frac{1}{6}\)

Question 7.
The figure shows how the yard lines on a football field are numbered. The goal lines are labeled G. A referee was standing on a certain yard line as the first quarter ended. He walked 41 \(\frac{3}{4}\) yards to a yard line with the same number as the one he had just left. How far was the referee from the nearest goal line?
1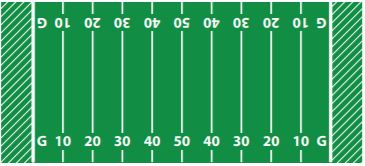
________ \(\frac{□}{□}\)

Answer: 29 \(\frac{1}{8}\)

Explanation:
The American football field is 100 yds long, 53 1/3 yards wide, and has 10-yard touchdown zones at each end of the field.
Let x = distance of the referee at the end of the quarter from the nearest goal.
The distance between the same yard lines on either side of the centerline is
100 – 2x
This distance is the 41 3/4 yards that the referee walked. Therefore
100 – 2x = 41.75
-2x = 41.75 – 100 = -58.25
x = 29.125 yd
Convert from decimal to fraction.
x = 29 \(\frac{1}{8}\) yards

In 8–10, a teacher gave a test with 50 questions, each worth the same number of points. Donovan got 39 out of 50 questions right. Marci’s score was 10 percentage points higher than Donovan’s.

Question 8.
What was Marci’s score? Explain.
________ %

Answer: 88 %

Explanation:
39/50 = 78/100
78/100 + 10/100 = 88/100 = 44/50
88/100 = 88%

Question 9.
How many more questions did Marci answer correctly? Explain.
________ questions

Answer: 5 questions

Explanation:
Marci got 44 correct and Donovan got 39 correct so she got 44 – 39 = 5 more questions correct.

Question 10.
Explain how you can check your answers for reasonableness.
Type below:
_____________

Answer:
You can check your answers for reasonableness by using estimates.
Donovan scored 39/50 which is about 40/50 = 80/100 = 80%
Ten percentage points higher is then 80% + 10% = 90% = 90/100 = 45/50.
Since Marci’s score was 44/50, it is a reasonable answer.

Applying Rational Number Operations – Page No. 100

For 11–13, use the expression 1.43 × \(\left(-\frac{19}{37}\right)\)

Question 11.
Critique Reasoning
Jamie says the value of the expression is close to −0.75. Does Jamie’s estimate seem reasonable? Explain.
_______

Answer: Yes

Explanation:
Jamie is correct. 1.43 is about 1.5 and -19/37 ≈ 1/2.
Since 1.5 × – 1/2 = -0.75
Jamie’s estimation is reasonable.

Question 12.
Find the product. Explain your method.
_______

Answer:
Using a calculator, you get that 1.43 × (-19/37) ≈ -0.734

Question 13.
Does your answer to Exercise 12 justify your answer to Exercise 11?
_______

Answer: Yes

Explanation:
-0.734 is close to the estimate of -0.75 so the answer to Exercise 12 justifies the answer to Exercise 11.

H.O.T

Focus On Higher Order Thinking

Question 14.
Persevere in Problem Solving
A scuba diver dove from the surface of the ocean to an elevation of −79 \(\frac{9}{10}\) feet at a rate of -18.8 feet per minute. After spending 12.75 minutes at that elevation, the diver ascended to an elevation of −28 \(\frac{9}{10}\) feet. The total time for the dive so far was 19 \(\frac{1}{8}\) minutes. What was the rate of change in the diver’s elevation during the ascent?
_______ ft/min

Answer: 24 ft/min

Explanation:
Given that,
A scuba diver dove from the surface of the ocean to an elevation of −79 \(\frac{9}{10}\) feet at a rate of -18.8 feet per minute.
After spending 12.75 minutes at that elevation, the diver ascended to an elevation of −28 \(\frac{9}{10}\) feet. The total time for the dive so far was 19 \(\frac{1}{8}\) minutes.
−79 \(\frac{9}{10}\) ÷ -18.8 = 4.25 minutes
Find the time it took to ascend by subtracting the descent time and time spent at the descent elevation from the total dive time.
19 \(\frac{1}{8}\) – 4.25 – 12.75 = 2 1/8 minutes
-28 \(\frac{9}{10}\) – (-−79 \(\frac{9}{10}\)) = 51 feet
Find the rate of change by dividing the distance in feet divided by the time.
51/2 1/8 = 24 feet per minute

Question 15.
Analyze Relationships
Describe two ways you could evaluate 37% of the sum of 27 \(\frac{3}{5}\) and 15.9. Tell which method you would use and why
Type below:
___________

Answer:
Method 1:
Rewrite numbers in fraction form and evaluate algebraically.
37% (27 \(\frac{3}{5}\) + 15.9)
37/100 (27 3/5 + 15 9/10)
37/100 (138/5 + 159/10)
37/100 (435/10)
37/100 × 87/2 = 3219/200 = 16.095
Method 2:
Rewrite numbers in decimal form and evaluate with a calculator
37% (27 \(\frac{3}{5}\) + 15.9)
0.37(27.6 + 15.9)
0.37 × 43.5 = 16.095

Question 16.
Represent Real-World Problems
Describe a real-world problem you could solve with the help of a yardstick and a calculator.
Type below:
___________

Answer:
Finding the perimeter of the table. Using the yardstick you can get the side length of the table and add these measurements to get the perimeter.

Module Quiz – 3.1 Rational Numbers and Decimals – Page No. 101

Write each mixed number as a decimal.

Question 1.
4 \(\frac{1}{5}\) =
_______

Answer: 4.2

Explanation:
To convert fractions to decimals, simply divide the numerator to the denominator. If the quotient goes on and on, it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{1}{5}\) = 0.2
4 + 0.2 = 4.2
4 \(\frac{1}{5}\) = 4.2

Question 2.
12 \(\frac{14}{15}\) =
_______

Answer: 12.933..

Explanation:
To convert fractions to decimals, simply divide the numerator to the denominator. If the quotient goes on and on, it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{14}{15}\) = 0.933..
12 + 0.933 = 12.933..
12 \(\frac{14}{15}\) = 12.933..

Question 3.
5 \(\frac{5}{32}\) =
_______

Answer: 5.15625

Explanation:
To convert fractions to decimals, simply divide the numerator to the denominator. If the quotient goes on and on, it is a repeating decimal, and to write this as a decimal, put a bar on top of the repeating digits.
\(\frac{5}{32}\) = 0.15625
5 + 0.15625 = 5.15625
5 \(\frac{5}{32}\) = 5.15625

3.2 Adding Rational Numbers

Find each sum.

Question 4.
4.5 + 7.1 =
_______

Answer: 11.6

Explanation:
To add or subtract numbers, make sure to align the digits vertically before doing the operation.
Make sure to align ones, tens, hundreds and thousands digits before adding
4.5
+7.1
 11.6

Question 5.
\(5 \frac{1}{6}+\left(-3 \frac{5}{6}\right)\) =
_______ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{3}\)

Explanation:
\(5 \frac{1}{6}+\left(-3 \frac{5}{6}\right)\) =
\(5 \frac{1}{6}\) – [/latex]3 \frac{5}{6}\right)[/latex] = 4 7/6 – 3 5/6
1 2/6 = 1 1/3
Thus \(5 \frac{1}{6}+\left(-3 \frac{5}{6}\right)\) = 1 \(\frac{1}{3}\)

3.3 Subtracting Rational Numbers

Find each difference.

Question 6.
\(-\frac{1}{8}-\left(6 \frac{7}{8}\right)\) =
_______

Answer: -7

Explanation:
Both numbers are negative. so add the opposites of each number and write the answer as a negative.
\(-\frac{1}{8}-\left(6 \frac{7}{8}\right)\)
-(\(\frac{1}{8}+\left(6 \frac{7}{8}\right)\))
= – 6 \(\frac{8}{8}\) = -6 – 1 = -7

Question 7.
14.2 − (−4.9) =
_______

Answer: 19.1

Explanation:
14.2 − (−4.9)
= 14.2 + 4.9 = 19.1

3.4 Multiplying Rational Numbers

Multiply.

Question 8.
\(-4\left(\frac{7}{10}\right)\) =
\(\frac{□}{□}\)

Answer: –\(\frac{14}{5}\)

Explanation:
Multiply the whole number with the numerator. write this product in the numerator and keep the same denominator.
\(-4\left(\frac{7}{10}\right)\) = –\(\frac{14}{5}\)

Question 9.
−3.2(−5.6)(4) =
_______

Answer: 71.68

Explanation:
Multiply the first two numbers. There are two negative signs so the answer will be positive.
−3.2(−5.6)(4) = 17.92 × 4 = 71.68

3.5 Dividing Rational Numbers

Find each quotient.

Question 10.
\(-\frac{19}{2} \div \frac{38}{7}\) =
\(\frac{□}{□}\)

Answer: –\(\frac{7}{4}\)

Explanation:
\(-\frac{19}{2} \div \frac{38}{7}\)
-19/2 × 7/38 = -7/2 × 1/2
= –\(\frac{7}{4}\)

Question 11.
\(\frac{-32.01}{-3.3}\) =
_______

Answer: 9.7

Explanation:
Given,
\(\frac{-32.01}{-3.3}\)
Remember that dividing two negatives gives a positive answer.
-32.01 ÷ -3.3 = 9.7

3.6 Applying Rational Number Operations

Question 12.
Luis bought stock at $83.60. The next day, the price increased by 15.35 dollars. This new price changed by −4 \(\frac{3}{4}\)% the following day. What was the final stock price? Is your answer reasonable? Explain.
$ _______

Answer: $94.25

Explanation:
83.60 + 15.35 = 98.95
98.95 × −4 \(\frac{3}{4}\)% = 98.95 × -0.0475 = 4.70
98.95 – 4.70 = $94.25

Essential Question

Question 13.
How can you use negative numbers to represent real-world problems?
Type below:
___________

Answer:
Negative numbers can be used in real-world problems to represents decreases or values that are below a level considered to be 0.

MODULE 3 MIXED REVIEW – Selected Response – Page No. 102

Question 1.
What is −7 \(\frac{5}{12}\) written as a decimal?
Options:
a. -7.25
b. -7.333…
c. -7.41666…
d. -7.512

Answer: -7.41666…

Explanation:
Given,
−7 \(\frac{5}{12}\)
Convert from fraction to decimal.
5 ÷ 12 = 0.4166..
−7 \(\frac{5}{12}\) = -7.4166….
Thus the correct answer is option C.

Question 2.
Glenda began the day with a golf score of -6 and ended with a score of -10. Which statement represents her golf score for that day?
Options:
a. -6 – (-10) = 4
b. -10 – (-6) = -4
c. -6 + (-10) = -16
d. -10 + (-6) = -16

Answer: -10 – (-6) = -4

Explanation:
Given,
Her golf score for the day can be found by subtracting her ending score and her beginning score which gives
-10 – (-6) = -10 + 6 = -4
So, the correct answer is option B.

Question 3.
A submersible vessel at an elevation of -95 feet descends to 5 times that elevation. What is the vessel’s new elevation?
Options:
a. -475 ft
b. -19 ft
c. 19 ft
d. 475 ft

Answer: -475 ft

Explanation:
Given,
A submersible vessel at an elevation of -95 feet descends to 5 times that elevation.
-95 feet × 5 = -475 feet
Thus the correct answer is option A.

Question 4.
The temperature at 7 P.M. at a weather station in Minnesota was -5 °F. The temperature began changing at the rate of -2.5 °F per hour. What was the temperature at 10 P.M.?
Options:
a. -15 °F
b. -12.5 °F
c. 2.5 °F
d. 5 °F

Answer: -12.5 °F

Explanation:
Find the total change in temperature by multiplying the rate of change per hour times the number of hours from 7 pm to 10 pm.
-5 + (-7.5) = -12.5°F
Thus the correct answer is option B.

Question 5.
What is the sum of -2.16 and -1.75?
Options:
a. 0.41
b. 3.91
c. -0.41
d. -3.91

Answer: -3.91

Explanation:
Both numbers are negative so add their opposites and make the answer negative.
-2.16 + (-1.75) = -(2.16 + 1.75) = -3.91
So, the correct answer is option D.

Question 6.
On Sunday, the wind chill temperature reached -36 °F. On Monday, the wind chill temperature only reached \(\frac{1}{4}\) of Sunday’s wind chill temperature. What was the lowest wind chill temperature on Monday?
Options:
a. -9 °F
b. -36 \(\frac{1}{4}\) °F
c. -40 °F
d. -144 °F

Answer: -9 °F

Explanation:
Given that,
On Sunday, the wind chill temperature reached -36 °F.
On Monday, the wind chill temperature only reached \(\frac{1}{4}\) of Sunday’s wind chill temperature.
-36 × \(\frac{1}{4}\) = -9°F
Thus the correct answer is option A.

Question 7.
The level of a lake was 8 inches below normal. It decreased 1 \(\frac{1}{4}\) inches in June and 2 \(\frac{3}{8}\) inches more in July. What was the new level with respect to the normal level?
Options:
a. -11 \(\frac{5}{8}\) in.
b. -10 \(\frac{5}{8}\) in.
c. -9 \(\frac{1}{8}\) in.
d. -5 \(\frac{3}{8}\) in.

Answer: -11 \(\frac{5}{8}\) in.

Explanation:
The level of a lake was 8 inches below normal. It decreased 1 \(\frac{1}{4}\) inches in June and 2 \(\frac{3}{8}\) inches more in July.
The initial level is below normal so it is represented by a negative number. The level continued to decrease in June and July so those changes are also represented by negative numbers.
Find the sum of these values to find what the new level was with respect to the normal level.
-8 – 1 \(\frac{1}{4}\) – 2 \(\frac{3}{8}\)
= -8 – \(\frac{5}{4}\) – \(\frac{19}{8}\)
= – \(\frac{93}{8}\)
= – 11 \(\frac{5}{8}\)
Thus the correct answer is option A.

Mini-Task

Question 8.
The average annual rainfall for a town is 43.2 inches.
a. What is the average monthly rainfall?
________

Answer:
If the average rainfall us 43.2 inches then the monthly rainfall is 43.2/12 = 3.6 inches since there are 12 months in a year.

Question 8.

b. The difference of a given month’s rainfall from the average monthly rainfall is called the deviation. What is the deviation for each month shown?
May: ___________ inch
June: ___________ inches
July: ___________ inches

Answer:
The deviation for May is 2 3/5 – 3.6 = 2.6 – 3.6 = -1 inches.
The deviation for June is 7/8 – 3.6 = -2.725 inches.
The deviation for July 4 1/4 – 3.6 = 0.65 inches.

Question 8.
c. The average monthly rainfall for the previous 9 months was 4 inches. Did the town exceed its average annual rainfall? If so, by how much?
________

Answer:
If is rained 4 inches for 9 months, the total amount of rain over the 12 month period is than 9(4) + 2 3/5 + 7/8 + 4 1/4
= 36 + 2.6 + 0.875 + 4.25 = 43.725.
Since this is greater than the average annual rainfall of 43.2, the town did exceed is average annual rainfall.
the difference of 43.725 and 43.2 is
43.725 – 43.2 = 0.525
so, it exceeded it by 0.525 inches.

Module 3 Review – Rational Numbers – Page No. 106

EXERCISES

Write each mixed number as a whole number or decimal. Classify each number according to the group(s) to which it belongs: rational numbers, integers, or whole numbers.

Question 1.
\(\frac{3}{4}\)
________

Answer: 0.75, rational

Explanation:
Write as a decimal by dividing 3 by 4. A shortcut with fourths is to think of the fractions in terms of money. 4 quarters make a dollar and 3 quarters is $0.75 so three-fourths is 0.75 in decimal form.
Since \(\frac{3}{4}\) could not be written as a whole number or integer, it is a rational number.

Question 2.
\(\frac{8}{2}\)
________

Answer: 4

Explanation:
\(\frac{8}{2}\) = 4
Since 4 doesn’t have a decimal and is positive, it is a whole number. All whole numbers are also integers and rational numbers so 4 is a rational number, integer, and a whole number.

Question 3.
\(\frac{11}{3}\)
________

Answer: 3.66

Explanation:
Rewrite as a mixed number and then divide 2 by 3 to get the decimal part of the number.
\(\frac{11}{3}\) = 3 2/3 = 3.666…
Since 3.66.. has a decimal, it is not an integer or whole number. Therefore it is a rational number only.

Question 4.
\(\frac{5}{2}\)
________

Answer: 2.5

Explanation:
Write as a mixed number and then divide 1 by 2 to get the decimal part of the number a shortcut is to think of the fraction in terms of money. Half a dollar is $0.50 so one half equals 0.50 = 0.50
Since 2.5 has a decimal, it is not an integer or whole number. Therefore 2.5 is a rational number only.

Find each sum or difference.

Question 5.
−5 + 9.5
________

Answer: 4.5

Explanation:
Rewrite as subtraction and then subtract.
-5 + 9.5 = 4.5

Question 6.
\(\frac{1}{6}\) + (−\(\frac{5}{6}\))
\(\frac{□}{□}\)

Answer: –\(\frac{2}{3}\)

Explanation:
Rewrite as subtraction and then subtract.
\(\frac{1}{6}\) + (−\(\frac{5}{6}\))
\(\frac{1}{6}\) −\(\frac{5}{6}\)
= –\(\frac{4}{6}\) = –\(\frac{2}{3}\)

Question 7.
−0.5 + (−8.5)
________

Answer: -9

Explanation:
Both numbers are negative so add their opposites and write the answers as a negative.
−0.5 + (−8.5) = -(0.5 + 8.5) = -9

Question 8.
−3 − (−8)
________

Answer: 5

Explanation:
Rewrite as addition since subtracting a negative is the same as adding a positive.
−3 − (−8) = -3 + 8 = 5

Question 9.
5.6 − (−3.1)
________

Answer: 8.7

Explanation:
Rewrite as addition since subtracting a negative is the same as adding a positive.
5.6 − (−3.1) = 5.6 + 3.1 = 8.7

Question 10.
3 \(\frac{1}{2}\) − 2 \(\frac{1}{4}\)
\(\frac{□}{□}\)

Answer: 1 \(\frac{1}{4}\)

Explanation:
Get common denominator.
3 \(\frac{1}{2}\) − 2 \(\frac{1}{4}\)
3 \(\frac{2}{4}\) − 2 \(\frac{1}{4}\) = 1 \(\frac{1}{4}\)

Find each product or quotient

Question 11.
−9 × (−5)
________

Answer: 45

Explanation:
Multiply two negative numbers make a positive number.
−9 × (−5) = 45

Question 12.
0 × (−7)
________

Answer: 0

Explanation:
Any number multiplied with 0 will be zero.
So, the product is 0.

Question 13.
−8 × 8
________

Answer: -64

Explanation:
Multiply since there is only one negative the answer is negative.
-8 × 8 = -64

Question 14.
\(\frac{-56}{8}\)
________

Answer: -7

Explanation:
Divide since there is only one negative the answer is negative.
8 divides 56 seven times.
\(\frac{-56}{8}\) = -7

Question 15.
\(\frac{-130}{-5}\)

Answer: 26

Explanation:
Divide since there are two negative signs the answer is positive.
\(\frac{-130}{-5}\) = 26

Question 16.
\(\frac{34.5}{1.5}\)
________

Answer: 23

Explanation:
Divide since both the numbers are positive the answer will be positive.
\(\frac{34.5}{1.5}\) = 23
1.5 divides 34.5 23 times.
So, the quotient is 23.

Question 17.
\(-\frac{2}{5}\left(-\frac{1}{2}\right)\left(-\frac{5}{6}\right)\)
\(\frac{□}{□}\)

Answer: –\(\frac{1}{6}\)

Explanation:
Multiply by cancelling the 2s and 5s an odd number of negatives makes a negative so the answer is negative.
\(-\frac{2}{5}\left(-\frac{1}{2}\right)\left(-\frac{5}{6}\right)\) = –\(\frac{1}{6}\)

Question 18.
\(\frac{1}{5}\left(-\frac{5}{7}\right)\left(\frac{3}{4}\right)\)
\(\frac{□}{□}\)

Answer: –\(\frac{3}{28}\)

Explanation:
\(\frac{1}{5}\left(-\frac{5}{7}\right)\left(\frac{3}{4}\right)\)
multiply by cancelling the 5s
\(\frac{1}{5}\left(-\frac{5}{7}\right)\left(\frac{3}{4}\right)\) = – 3/7×4 = -3/28
Thus \(\frac{1}{5}\left(-\frac{5}{7}\right)\left(\frac{3}{4}\right)\) = –\(\frac{3}{28}\)

Question 19.
Lei withdrew $50 from her bank account every day for a week. What was the change in her account in that week?
$ ________

Answer: -$350

Explanation:
Lei withdrew $50 from her bank account every day for a week.
Convert from week to days
1 week = 7 days
7 × -50 = -350
The change in her account is -$350.

Question 20.
Dan is cutting 4.75 foot lengths of twine from a 240 foot spool of twine. He needs to cut 42 lengths, and says that 40.5 feet of twine will remain. Show that this is reasonable.
Type below:
__________

Answer:
The estimation of 4.75 is 5 and 42 is 40.
5 × 40 = 200
So he will be using about 200 feet.
He has 240 feet so he will have about 240-200 = 40 feet remaining.
Since 40 ≈ 40.5
The answer is reasonable.

Unit 1 Performance Tasks – Page No. 107

Question 1.
Armand is an urban planner, and he has proposed a site for a new town library. The site is between City Hall and the post office on Main Street.

The distance between City Hall and the post office is 612 miles. City Hall is 114 miles closer to the library site than it is to the post office.
a. Write 6 \(\frac{1}{2}\) miles and 1 \(\frac{1}{4}\) miles as decimals
6 \(\frac{1}{2}\) = __________
1 \(\frac{1}{4}\) = __________

Answer:
Write as decimal by dividing 1 by 2 and dividing 1 by 4 a shortcut is to think about ur in terms of money. Half of a dollae is $0.50 and a quarter is $0.25
So 1/2 = 0.50 = 0.5
1/4 = 0.25
6 1/2 = 6.5 and 1 1/4 = 1.25

Question 1.
b. Let d represent the distance from City Hall to the library site. Write an expression for the distance from the library site to the post office.
__________

Answer:
The library is closer to City Hall than the post office is so d is the difference between the distance from City Hall to the Post Office and the distance between City Hall and the Library Site.
d = 6 1/2 – 1 1/4

Question 1.
c. Write an equation that represents the following statement: The distance from City Hall to the library site plus the distance from the library site to the post office is equal to the distance from City Hall to the post office.
Type below:
__________

Answer:
The distance from the City Hall to the library is d, the distance from the library to the post office is 1 1/4 since the library is 1 1/4 miles closer to City Hall than the post office is, the distance from City Hall to the Post Office is 6 1/4
d + 1 1/4 = 6 1/4

Question 1.
d. Solve your equation from part c to determine the distance from City Hall to the library site, and the distance from the post office to the library site.
City Hall to library site: __________ miles
Library site to post office: __________ miles

Answer:
d = 6 1/2 – 1 1/4
d = 6 2/4 – 1 1/4
d = 5 1/4
Thus the distance is 5 1/4 miles.

Question 2.
Sumaya is reading a book with 288 pages. She has already read 90 pages. She plans to read 20 more pages each day until she finishes the book.
a. Sumaya writes the equation 378 = -20d to find the number of days she will need to finish the book. Identify the errors that Sumaya made.
Type below:
__________

Answer:
She made the mistake of using -20 in the equation instead of a positive 20. The negative can’t be used since she is not reading a negative number of pages per day.
She also made the mistake of adding 90 to 288 instead of subtracting.
Since she has already read 90 pages she has less than 288 pages left to read, not more.
288 – 90 = 198
The correct equation is 198 = 20d

Question 2.
b. Write and solve an equation to determine how many days Sumaya will need to finish the book. In your answer, count part of a day as a full day. Show that your answer is reasonable.
______ days

Answer:

198 = 20d is dividing both sides by 20 gives d = 198/20 = 9.9
Rounding this up gives 10 days.
This answer is reasonable since the books is about 300 pages and she has read about 100 pages of the book leaving about 200 pages left to read.
She is reading 20 pages per day and 20 × 10 = 200
So it would take 10 days to read about 200 pages.

Question 2.
c. Estimate how many days you would need to read a book about the same length as Sumaya’s book. What information did you use to find the estimate?
Type below:
__________

Answer:
Sumaya’s book is about 300 pages. Reading 20 pages a day would mean it would take about 300/20 = 15 days to read the book.

Unit 1 Performance Tasks – Page No. 108

Question 3.
Jackson works as a veterinary technician and earns $12.20 per hour.
a. Jackson normally works 40 hours a week. In a normal week, what is his total pay before taxes and other deductions?
$ ______

Answer: $488

Explanation:
Jackson works as a veterinary technician and earns $12.20 per hour.
Jackson normally works 40 hours a week.
40 × $12.20 = $488
Thus the total pay before taxes and other deductions is $488.

Question 3.
b. Last week, Jackson was ill and missed some work. His total pay before deductions was $372.10. Write and solve an equation to find the number of hours Jackson worked.
______ hours

Answer: 30.5 hours

Explanation:
Jackson works as a veterinary technician and earns $12.20 per hour.
His total pay before deductions was $372.10.
$12.20h = $372.10
h = 372.10/12.20
h = 30.5 hours

Question 3.
c. Jackson records his hours each day on a time sheet. Last week when he was ill, his time sheet was incomplete. How many hours are missing? Show your work. Then show that your answer is reasonable.

______ hours

Answer: 6.75 hours

Explanation:
8 + 7.25 + 8.5 = 23.75
30.5 – 23.75 = 6.75 hours

Question 3.
d. When Jackson works more than 40 hours in a week, he earns 1.5 times his normal hourly rate for each of the extra hours. Jackson worked 43 hours one week. What was his total pay before deductions? Justify your answer.
$ __________________

Answer: $542.90

Explanation:
When Jackson works more than 40 hours in a week, he earns 1.5 times his normal hourly rate for each of the extra hours.
Jackson worked 43 hours one week.
40 × 12.20 + 3 × 1.5 × 12.20 = $488 + $54.90 = $542.90

Question 3.
e. What is a reasonable range for Jackson’s expected yearly pay before deductions? Describe any assumptions you made in finding your answer.
$ __________________

Answer:

Assuming he works between 40 and 45 hours per week, his weekly pay range is between 40 × 12.20 = $488
40 × 12.20 + 5 × 1.5 × 12.20 = 488 + 91.50 = $579.50
Since there are 52 weeks in a year, his yearly pay is between 52 × 488 ≈ $25,000
and 52 × $579.50 ≈ $30,000.

Unit 1 MIXED REVIEW – Selected Response – Page No. 109

Question 1.
What is −6 \(\frac{9}{16}\) written as a decimal?
Options:
a. -6.625
b. -6.5625
c. -6.4375
d. -6.125

Answer: -6.5625

Explanation:
−6 \(\frac{9}{16}\)
Divide 9 by 16 to get 9/16 = 0.5625.
6 \(\frac{9}{16}\) = 6 + 0.5625 = 6.5625
−6 \(\frac{9}{16}\) = -6.5625
Thus the correct answer is option B.

Question 2.
Working together, 6 friends pick 14 \(\frac{2}{5}\) pounds of pecans at a pecan farm. They divide the pecans equally among themselves. How many pounds does each friend get?
Options:
a. 20 \(\frac{2}{5}\) pounds
b. 8 \(\frac{2}{5}\) pounds
c. 2 \(\frac{3}{5}\) pounds
d. 2 \(\frac{2}{5}\) pounds

Answer: \(\frac{2}{5}\) pounds

Explanation:
Divide the number of pounds by the number of friends to get the number of pounds each friend gets.
14 \(\frac{2}{5}\)/6 = 14.4/6 = 2.4 pounds.
2.4 = 2 \(\frac{2}{5}\) pounds
Thus the correct answer is option D.

Question 3.
What is the value of (−3.25)(−1.56)?
Options:
a. -5.85
b. -5.07
c. 5.07
d. 5.85

Answer: 5.07

Explanation:
Multiply two negatives make a positive.
So the answer is positive.
(−3.25)(−1.56) = 5.07
The answer is option C.

Question 4.
Mrs. Rodriguez is going to use 6 \(\frac{1}{3}\) yards of material to make two dresses. The larger dress requires 3 \(\frac{2}{3}\) yards of material. How much material will Mrs. Rodriguez have left to use on the smaller dress?
Options:
a. 1 \(\frac{2}{3}\) yards
b. 2 \(\frac{1}{3}\) yards
c. 2 \(\frac{2}{3}\) yards
d. 3 \(\frac{1}{3}\) yards

Answer: 2 \(\frac{2}{3}\) yards

Explanation:
Subtract the yards of material for the larger dress from the total yards of material.
6 \(\frac{1}{3}\) yards – 3 \(\frac{2}{3}\) yards = 2 \(\frac{2}{3}\) yards
Thus the correct answer is option C.

Question 5.
Jaime had $37 in his bank account on Sunday. The table shows his account activity for the next four days. What was the balance in Jaime’s account after his deposit on Thursday?

Options:
a. $57.49
b. $59.65
c. $94.49
d. $138.93

Answer: $94.49

Explanation:
Add up all the deposits and withdrawals to his original balance make sure deposits are represented by positive numbers and withdrawals are represented by negative numbers.
37 + 17.42 – 12.60 – 9.62 + 62.29 = 94.49
Thus the correct answer is option C.

Question 6.
A used motorcycle is on sale for $3,600. Erik makes an offer equal to \(\frac{3}{4}\) of this price. How much does Erik offer for the motorcycle?
Options:
a. $4800
b. $2700
c. $2400
d. $900

Answer: $2700

Explanation:
Given that,
A used motorcycle is on sale for $3,600. Erik makes an offer equal to \(\frac{3}{4}\) of this price.
\(\frac{3}{4}\) × 3600 = 2700
Thus the correct answer is option B.

Question 7.
Ruby ate \(\frac{1}{3}\) of a pizza, and Angie ate \(\frac{1}{5}\) of the pizza. How much of the pizza did they eat in all?
Options:
a. 1 \(\frac{1}{5}\) of the pizza
b. \(\frac{1}{8}\) of the pizza
c. \(\frac{3}{8}\) of the pizza
d. \(\frac{8}{15}\) of the pizza

Answer: \(\frac{8}{15}\) of the pizza

Explanation:
Ruby ate \(\frac{1}{3}\) of a pizza, and Angie ate \(\frac{1}{5}\) of the pizza.
\(\frac{1}{3}\) = \(\frac{1}{5}\) = \(\frac{5}{15}\) + \(\frac{3}{15}\) = \(\frac{8}{15}\)
Thus the correct answer is option D.

Unit 1 MIXED REVIEW – Page No. 110

Question 8.
Winslow buys 1.2 pounds of bananas. The bananas cost $1.29 per pound. To the nearest cent, how much does Winslow pay for the bananas?
Options:
a. $1.08
b. $1.20
c. $1.55
d. $2.49

Answer: $1.55

Explanation:
Winslow buys 1.2 pounds of bananas. The bananas cost $1.29 per pound.
1.2 × $1.29 = $1.548 ≈ $1.55
Thus the correct answer is option C.

Question 9.
The temperature was -10 °F and dropped by 16 °F. Which statement represents the resulting temperature in degrees Fahrenheit?
Options:
a. -10 – (-16) = -6
b. -10 – 16 = -26
c. 10 – (-16) = 26
d. -10 + 16 = 6

Answer: -10 – 16 = -26

Explanation:
The temperature was -10 °F and dropped by 16 °F.
-10 + (-16) = -26°F.
So, the correct answer is option B.

Question 10.
A scuba diver at a depth of -12 ft (12 ft below sea level), dives down to a coral reef that is 3.5 times the diver’s original depth. What is the diver’s new depth?
Options:
a. -420 ft
b. -42 ft
c. 42 ft
d. about 3.4 ft

Answer: -42 ft

A scuba diver at a depth of -12 ft, dives down to a coral reef that is 3.5 times the diver’s original depth.
-12 × 3.5 = -42 ft
So, the correct answer is option B.

Question 11.
The school Spirit Club spent $320.82 on food and took in 643.59 selling the food. How much did the Spirit Club make?
Options:
a. -$322.77
b. -$964.41
c. $322.77
d. $964.41

Answer: $322.77

Explanation:
The school Spirit Club spent $320.82 on food and took in 643.59 selling the food.
$643.59 – $320.82 = $322.77
So, the answer is option C.

Question 12.
Lila graphed the points -2 and 2 on a number line. What does the distance between these two points represent?
Options:
a. the sum of -2 and 2
b. the difference of 2 and -2
c. the difference of -2 and 2
d. the product of -2 and 2

Answer: the difference of 2 and -2

Explanation:
Distance is found by subtracting the larger number and the smaller number so it is the difference of 2 and -2.
Thus the correct answer is option B.

Question 13.
What is a reasonable estimate of −3 \(\frac{4}{5}\) + (−5.25) and the actual value?
Options:
a. -4 + (-5) = -9; −9 \(\frac{1}{20}\)
b. -3 + (-5) = -8; −8 \(\frac{1}{20}\)
c. -4 + (-5) = -1; −8 \(\frac{9}{20}\)
d. -3 + (-5) = 8; 8 \(\frac{1}{20}\)

Answer: -4 + (-5) = -9; −9 \(\frac{1}{20}\)

Explanation:
−3 \(\frac{4}{5}\) + (−5.25)
−3 \(\frac{4}{5}\) ≈ -4
−5.25 ≈ -5
So the sum is about -4 + -5 = -9.
The estimated answer is -9.

Mini-Task

Question 14.
Juanita is watering her lawn using the water stored in her rainwater tank. The water level in the tank drops \(\frac{1}{3}\) inch every 10 minutes she waters.
a. What is the change in the tank’s water level after 1 hour?
______ inches

Answer: -2 inches

Explanation:
Juanita is watering her lawn using the water stored in her rainwater tank.
There are six 10 minute intervals in 1 hour so change is
6 × –\(\frac{1}{3}\) = -2 inches
Therefore, the tank’s water level after 1 hour is -2 inches.

Question 14.
b. What is the expected change in the tank’s water level after 2.25 hours?
______ inches

Answer: -4.5 inches

Explanation:
Since the water level drops 2 inches every hour, in 2.25 hours the water level change will be -2 × 2.25 = -4.5 inches
Thus the expected change in the tank’s water level after 2.25 hours is -4.5 inches.

Question 14.
c. If the tank’s water level is 4 feet, how many days can Juanita water if she waters for 15 minutes each day?
______ days

Answer: 96 days

Explanation:
15 minutes is 1/4 of an hour so in 15 minutes the water level will have dropped by 2 × 1/4 = 1/2 inches.
Since the water level is initially 4 feet = 48 inches
She can water for 48/1/2 = 48 × 2 = 96 days
It takes 96 days if she waters for 15 minutes.

Conclusion:

Hope the info prevailed in this article is beneficial for all the students. Keep in touch with us to get the latest updates regarding Go Math Grade 7 Answer Key Chapter 3 Rational Numbers. Also, the students of 4th grade can get the solutions for all the chapters on Go Math Grade 7 Answer Key page.