Go Math Grade 4 Answer Key Chapter 4 Divide by 1-Digit Numbers is the most important learning guide to learn the subject properly. It is a quick preparation & practice purpose material for students and educators. So, We have provided the solutions for all the questions with a brief explanation in this Go Math HMH Grade 4 Chapter 4 Answer Key. All these solutions are prepared by the Math Experts. Students and parents are suggested to Download Go Math Grade 4 Answer Key Chapter 4 Divide by 1-Digit Numbers pdf from here for free.
Go Math Grade 4 Answer Key Chapter 4 Divide by 1-Digit Numbers
Avail all detailed solutions to the questions via Go Math Answer Key of grade 4 chapter 4 and aid while doing homework and also while preparing for the exams. Just tap on the respective lesson link from chapter 4 Divide by 1-Digit Numbers and solve the questions. Along with the exercise and homework problems, we have also listed the answers for the mid-chapter checkpoint and review test in the Go Math Grade 4 Solution Key Chapter 4 Divide by 1-Digit Numbers.
Chapter 4 Divide by 1-Digit Numbers – Lesson: 1
Chapter 4 Divide by 1-Digit Numbers – Lesson: 2
Chapter 4 Divide by 1-Digit Numbers – Lesson: 3
Chapter 4 Divide by 1-Digit Numbers – Lesson: 4
Chapter 4 Divide by 1-Digit Numbers – Lesson: 5
Chapter 4 Divide by 1-Digit Numbers – Lesson: 6
Chapter 4 Divide by 1-Digit Numbers – Lesson: 7
- Page No. 218
- Divide Tens, Hundreds, and Thousands – Common Core – Page No. 219
- Common Core – Lesson Check – Page No. 220
Chapter 4 Divide by 1-Digit Numbers – Lesson: 8
Chapter 4 Divide by 1-Digit Numbers – Lesson: 9
- Estimate Quotients Using Compatible Numbers – Common Core – Page No. 224
- Common Core – Lesson Check – Page No. 226
Chapter 4 Divide by 1-Digit Numbers – Lesson: 10
Chapter 4 Divide by 1-Digit Numbers – Lesson: 11
- Division and the Distributive Property – Common Core – Page No. 231
- Common Core – Lesson Check – Page No. 232
Mid Chapter Checkpoint
Chapter 4 Divide by 1-Digit Numbers – Lesson: 12
Chapter 4 Divide by 1-Digit Numbers – Lesson: 13
- Divide Using Repeated Subtraction – Common Core – Page No. 239
- Common Core – Lesson Check – Page No. 240
Chapter 4 Divide by 1-Digit Numbers – Lesson: 14
Chapter 4 Divide by 1-Digit Numbers – Lesson: 15
- Divide Using Partial Quotients – Common Core – Page No. 245
- Common Core – Lesson Check – Page No. 246
Chapter 4 Divide by 1-Digit Numbers – Lesson: 16
Chapter 4 Divide by 1-Digit Numbers – Lesson: 17
- Model Division with Regrouping – Common Core – Page No. 251
- Common Core – Lesson Check – Page No. 252
Chapter 4 Divide by 1-Digit Numbers – Lesson: 18
Chapter 4 Divide by 1-Digit Numbers – Lesson: 19
Chapter 4 Divide by 1-Digit Numbers – Lesson: 20
Chapter 4 Divide by 1-Digit Numbers – Lesson: 21
Chapter 4 Divide by 1-Digit Numbers – Lesson: 22
Chapter 4 Divide by 1-Digit Numbers – Lesson: 23
- Problem Solving Multistep Division Problems – Common Core – Page No. 269
- Common Core – Lesson Check – Page No. 270
Chapter 4 – Review/Test
- Review/Test – Page No. 271
- Review/Test – Page No. 272
- Review/Test – Page No. 273
- Review/Test – Page No. 274
- Review/Test – Page No. 275
- Review/Test – Page No. 276
- Review/Test – Page No. 280
- Review/Test – Page No. 281
- Review/Test – Page No. 282
Common Core – Page No. 201
Estimate Quotients Using Multiples
Find two numbers the quotient is between. Then estimate the quotient.
Question 1.
175 ÷ 6
Think: 6 × 20 = 120 and 6 × 30 = 180. So, 175 ÷ 6 is between 20 and 30. Since 175 is closer to 180 than to 120, the quotient is about 30.
between 20 and 30
about 30
Answer: About 30
Explanation:
6 × 20 = 120 and 6 × 30 = 180. 175 is between 120 and 180. 175 ÷ 6 is closest to 20 and 30. So, 175 ÷ 6 is between 20 and 30. So, 175 ÷ 6 will be about 30.
Question 2.
53 ÷ 3
between ______ and
about ______
Answer: About 18
Explanation:
17 × 3= 51 and 18 × 3 = 54. 53 is between 51 and 54. 53 ÷ 3 is closest to 17 and 18. So, 53 ÷ 3 is between 17 and 18. So, 53 ÷ 3 will be about 18.
Question 3.
75 ÷ 4
between ______ and
about ______
Answer: About 19
Explanation:
18 × 4= 72 and 19 × 4= 76. 75 is between 72 and 76. 75 ÷ 4 is closest to 18 and 19. So, 75÷ 4 is between 18 and 19. So, 75 ÷ 4 will be about 19.
Question 4.
215 ÷ 9
between ______ and
about ______
Answer: About 24
Explanation:
23 × 9= 207 and 24 × 9 = 216. 24 is between 207 and 216. 215 ÷ 9 is closest to 23 and 24. So, 215 ÷ 9 is between 23 and 24. So, 215 ÷ 9 will be about 24.
Question 5.
284 ÷ 5
between ______ and
about ______
Answer: About 57
Explanation:
56 × 5 = 280 and 57 × 5 = 285. 284 is between 280 and 285. 284 ÷ 5 is closest to 56 and 57. So, 284 ÷ 5 is between 56 and 57. So, 175 ÷ 6 will be about 57.
Question 6.
191 ÷ 3
between ______ and
about ______
Answer: About 64
Explanation:
63 × 3 = 189 and 64 × 3 = 192. 191 is between 189 and 192. 191 ÷ 3 is closest to 63 and 64. So, 191 ÷ 3 is between 63 and 64. So, 175 ÷ 6 will be about 64.
Question 7.
100 ÷ 7
between ______ and
about ______
Answer: About 14
Explanation:
14 × 7 = 98 and 15 × 7 = 105. 100 is between 98 and 105. 100 ÷ 7 is closest to 14 and 15. So, 100 ÷ 7 is between 14 and 15. So, 100 ÷ 7 will be about 14.
Question 8.
438 ÷ 7
between ______ and
about ______
Answer: About 63
Explanation:
63 × 7 = 441 and 62 × 7 = 434. 438 is between 434 and 441. 438 ÷ 7 is closest to 62 and 63. So, 438 ÷ 7 is between 62 and 63. So, 438 ÷ 7 will be about 63.
Question 9.
103 ÷ 8
between ______ and
about ______
Answer: About 13
Explanation:
13 × 8 = 104 and 12 ×8 = 96. 103 is between 96 and 104. 103 ÷ 8 is closest to 12 and 13. So, 103 ÷ 8 is between 12 and 13. So, 103 ÷ 8 will be about 13.
Question 10.
255 ÷ 9
between ______ and
about ______
Answer: About 28
Explanation:
28 × 9 = 252 and 29 × 9 = 261. 255 is between 252 and 261. 255 ÷ 9 is closest to 28 and 29. So, 255 ÷ 9 is between 28 and 29. So, 255 ÷ 9 will be about 28.
Problem Solving
Question 11.
Joy collected 287 aluminum cans in 6 hours. About how many cans did she collect per hour?
about ______ cans
Answer: About 48 cans
Explanation:
47 × 6 = 282 and 48 × 6 = 288. 287 is between 282 and 288. 287 ÷ 6 is closest to 47 and 48. So, 287 ÷ 6 is between 47 and 48. So, 287 ÷6 will be about 48.
Question 12.
Paul sold 162 cups of lemonade in 5 hours. About how many cups of lemonade did he sell each hour?
about ______ cups
Answer: About 32 cups of lemonade he sold in each hour
Explanation:
32 × 5 = 160 and 33 × 5 = 165. 162 is between 160 and 165. 162 ÷ 5 is closest to 32 and 33. So, 162 ÷ 5 is between 32 and 33. So, 162 ÷ 5 will be about 32.
Common Core – Page No. 202
Lesson Check
Question 1.
Abby did 121 sit-ups in 8 minutes. Which is the best estimate of the number of sit-ups she did in 1 minute?
Options:
a. about 12
b. about 15
c. about 16
d. about 20
Answer: b. About 15
Explanation:
15 × 8 = 120 and 16 × 8 = 128. 121 is between 120 and 128. 121 ÷ 8 is closest to 120 and 128. So, 121 ÷ 8 is between 15 and 16. So, 121 ÷ 8 will be about 15.
Question 2.
The Garibaldi family drove 400 miles in 7 hours. Which is the best estimate of the number of miles they drove in 1 hour?
Options:
a. about 40 miles
b. about 57 miles
c. about 60 miles
d. about 70 miles
Answer: b. About 57 miles
Explanation:
57 × 7 = 399 and 58 × 7 = 406. 400 is between 399 and 406. 400 ÷ 7 is closest to 57 and 58. So, 400 ÷ 7 is between 57 and 58. So, 400 ÷ 7 will be about 57.
Spiral Review
Question 3.
Twelve boys collected 16 aluminium cans each. Fifteen girls collected 14 aluminium cans each. How many more cans did the girls collect than the boys?
Options:
a. 8
b. 12
c. 14
d. 18
Answer: 18
Explanation:
Number of aluminium cans boys had= 12× 16=192
Number of aluminium cans girls had = 15× 14=210
Girls collected more cans compared to boys,
Number of more cans collected by girls= 210-192=18
Question 4.
George bought 30 packs of football cards. There were 14 cards in each pack. How many cards did George buy?
Options:
a. 170
b. 320
c. 420
d. 520
Answer: c. 420
Explanation:
Number of packs of football cards= 30
Number of cards in each pack= 14
Total number of cards George bought=30×14=420
Question 5.
Sarah made a necklace using 5 times as many blue beads as white beads. She used a total of 30 beads. How many blue beads did Sarah use?
Options:
a. 5
b. 6
c. 24
d. 25
Answer: d. 25
Explanation:
Let the number of white beads be x while the number of blue beads are 5x.
Total number of beads in the necklace=30 beads
According to the problem,
5x+x=30
6x=30
x=30/6=5
Therefore the number of blue beads in the necklace are 5x= 5×5=25
Question 6.
This year, Ms. Webster flew 145,000 miles on business. Last year, she flew 83,125 miles on business. How many more miles did Ms. Webster fly on business this year?
Options:
a. 61,125 miles
b. 61,875 miles
c. 61,985 miles
d. 62,125 miles
Answer: b. 61,875 miles
Explanation:
Number of miles Ms Webster flew in this year= 145,000 miles
Number of miles Ms Webster flew in the last year=83,125 miles
Number of more miles travelled by Ms Webster =145,000-83,125=61,875
Page No. 205
Use counters to find the quotient and remainder.
Question 1.
10 ÷ 3
_____ R ______
Answer: Quotient: 3 Remainder: 1
Explanation:
Quotient:
A. Use 10 counters to represent the 10 dominoes. Then draw 3 circles to represent the divisor.
B. Share the counters equally among the 3 groups by placing them in the circles.
C. Number of groups of counters formed = quotient of 10 ÷ 3
D. Number of circles equally filled are 3, therefore, the quotient is 3
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 1
For 10 ÷ 3, the quotient is 3 and the remainder is 1, or 3 r1.
Question 2.
28 ÷ 5
_____ R ______
Answer: Quotient: 5 Remainder: 3
Explanation:
Quotient:
A. Use 28 counters to represent the 28 dominoes. Then draw 5 circles to represent the divisor.
B. Share the counters equally among the 5 groups by placing them in the circles.
C. Number of groups of counters formed = quotient of 28÷ 5
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 3
For 28 ÷ 5, the quotient is 5 and the remainder is 3, or 5 r3.
Question 3.
15 ÷ 6
_____ R ______
Answer: Quotient:2 Remainder:3
Explanation:
Quotient:
A. Use 15 counters to represent the 15 dominoes. Then draw 6 circles to represent the divisor.
B. Share the counters equally among the 6 groups by placing them in the circles.
C. Number of circles filled= quotient of 28 ÷ 6
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 3
For 28 ÷ 6, the quotient is 2 and the remainder is 3, or 2 r3.
Question 4.
11 ÷ 3
_____ R ______
Answer:Quotient:3 Remainder:2
Explanation:
Quotient:
A. Use 11 counters to represent the 3 dominoes. Then draw 3 circles to represent the divisor.
B. Share the counters equally among the 3 groups by placing them in the circles.
C. Number of circles filled = quotient of 11 ÷ 3
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 2
For 11 ÷ 3, the quotient is 3 and the remainder is 2, or 3 r2.
Question 5.
29 ÷ 4
_____ R ______
Answer: Quotient:7 Remainder:1
Explanation:
Quotient:
A. Use 29 counters to represent the 29 dominoes. Then draw 4 circles to represent the divisor.
B. Share the counters equally among the 4 groups by placing them in the circles.
C. Number of circles filled = quotient of 29 ÷ 4
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 1
For 29 ÷ 3, the quotient is 7 and the remainder is 1, or 7 r1.
Question 6.
34 ÷ 5
_____ R ______
Answer:Quotient: 6 Remainder: 4
Explanation:
Quotient:
A. Use 34 counters to represent the 34 dominoes. Then draw 5 circles to represent the divisor.
B. Share the counters equally among the 5 groups by placing them in the circles.
C. Number of circles filled = quotient of 34 ÷ 5
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 4
For 34 ÷ 5, the quotient is 6 and the remainder is 4, or 6 r4.
Question 7.
25 ÷ 3
_____ R ______
Answer:Quotient: 8 Remainder: 1
Explanation:
Quotient:
A. Use 25 counters to represent the 25 dominoes. Then draw 3 circles to represent the divisor.
B. Share the counters equally among the 3 groups by placing them in the circles.
C. Number of circles filled= quotient of 25 ÷ 3
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 1
For 25 ÷ 3, the quotient is 8 and the remainder is 1, or 8 r1.
Question 8.
7)\(\overline { 20 } \)
_____ R ______
Answer: Quotient:2 Remainder:6
Explanation:
Quotient:
A. Use 20 counters to represent the 20 dominoes. Then draw 7 circles to represent the divisor.
B. Share the counters equally among the 7 groups by placing them in the circles.
C. Number of circles filled= quotient of 7 qw20
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 1
Divide. Draw a quick picture to help.
Question 9.
4)\(\overline { 35 } \)
_____ R ______
Answer: Quotient: 8 Remainder:3





Explanation:
Quotient:
A. Use 35 counters to represent the 35 dominoes. Then draw 4 circles to represent the divisor.
B. Share the counters equally among the 4 groups by placing them in the circles.
C. Number of circles filled= quotient of \(\overline { 35 } \)=8
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 3
Question 10.
23 ÷ 8
_____ R ______
Answer: Quotient: 2 Remainder: 7









Explanation:
Quotient:
A. Use 23 counters to represent the 23 dominoes. Then draw 8 circles to represent the divisor.
B. Share the counters equally among the 8 groups by placing them in the circles.
C. Number of circles filled= quotient of 23 ÷ 8 = 2
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 7
Question 11.
Explain how you use a quick picture to find the quotient and remainder.
Type below:
_________
Answer: Quick pictures can be used to find the quotient and the remainder visually and accurately.
Explanation:
Example: 39÷ 5.
Use 39 counters.
Share the counters equally among 5 groups. The number of counters left over is the remainder.
For 39 ÷ 5, the quotient is 7 and the remainder is 2, or 7 r2.
When a number cannot be divided evenly, the amount left over is called the remainder.
Question 12.
Alyson has 46 beads to make bracelets. Each bracelet has 5 beads. How many more beads does Alyson need so that all the beads she has are used? Explain.
_____ more beads
Answer: 4 beads
Explanation:
Number of beads Alyson has= 46
Number of beads each bracelet needs=5
The number of bracelets which can be made = 46÷5

Since, the remainder is one we can say that one bead is leftover after making 9 bracelets.
Therefore, 4 beads should be added to 1 so that all the beads are used up.
Question 13.
For 13a–13d, choose Yes or No to tell whether the division expression has a remainder.
a. 36 ÷ 9
i. yes
ii. no
Answer: ii. no
Explanation:

Question 13.
b. 23 ÷ 3
i. yes
ii. no
Answer: i. yes
Explanation:

Question 13.
c. 82 ÷ 9
i. yes
ii. no
Answer: i. yes
Explanation:

Question 13.
d. 28 ÷ 7
i. yes
ii. no
Answer: ii. no
Explanation:

Page No. 206
Question 14.
Macy, Kayley, Maddie, and Rachel collected 13 marbles. They want to share the marbles equally. How many marbles will each of the 4 girls get? How many marbles will be left over?
Oscar used a model to solve this problem. He says his model represents 4)\(\overline { 13 } \). What is his error?

Look at the way Oscar solved this problem. Find and describe his error.
_________________________________________________________
Draw a correct model and solve the problem.
So, each of the 4 girls will get _______ marbles and _______ marble will be left over.
Type below:
_________
Answer: Quotient: 3 Remainder: 1
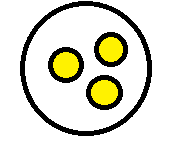




Explanation:
Quotient:
A. Use 13 counters to represent the 13 dominoes. Then draw 4 circles to represent the divisor.
B. Share the counters equally among the 4 groups by placing them in the circles.
C. Number of circles filled= quotient of 13 ÷ 4 = 3
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 1
Therefore each girl will get 3 marbles.
Common Core – Page No. 207
Remainders
Use counters to find the quotient and remainder.
Question 1.
13 ÷ 4
3 r1
Answer: 3 r1
Explanation:
Quotient:
A. Use 13 counters to represent the 13 dominoes. Then draw 4 circles to represent the divisor.
B. Share the counters equally among the 4 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 13 ÷ 4
D. Number of circles are equally filled with 4 counters, therefore, the quotient is 3
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 1
For 13 ÷ 4, the quotient is 3 and the remainder is 1, or 3 r1.
Question 2.
24 ÷ 7
_____ R ______
Answer: 3 r3
Explanation:
Quotient:
A. Use 24 counters to represent the 24 dominoes. Then draw 7 circles to represent the divisor.
B. Share the counters equally among the 7 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 24 ÷ 7
D. Number of circles are equally filled with 3 counters, therefore, the quotient is 3
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 3
For 24 ÷ 7, the quotient is 3 and the remainder is 3, or 3 r3.
Question 3.
39 ÷ 5
_____ R ______
Answer: 7 r4
Explanation:
Quotient:
A. Use 39 counters to represent the 39dominoes. Then draw 5 circles to represent the divisor.
B. Share the counters equally among the 5 groups by placing them in the circles.
C. Number of counters formed in each group = quotient 39 ÷ 5
D. Number of circles are equally filled with 7 counters, therefore, the quotient is 7
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 4
For 39 ÷ 5, the quotient is 7 and the remainder is 4, or 7 r4.
Question 4.
36 ÷ 8
_____ R ______
Answer: 4 r4
Explanation:
Quotient:
A. Use 36 counters to represent the 36 dominoes. Then draw 8 circles to represent the divisor.
B. Share the counters equally among the 8 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 36 ÷ 8
D. Number of circles are equally filled with 4 counters, therefore, the quotient is 4
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 4
For 36 ÷ 8, the quotient is 4 and the remainder is 4, or 4 r4.
Question 5.
6)\(\overline { 27 } \)
_____ R ______
Answer: 4 r3
Explanation:
Quotient:
A. Use 27 counters to represent the 27 dominoes. Then draw 6 circles to represent the divisor.
B. Share the counters equally among the 6 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 27 ÷6
D. Number of circles are equally filled with 4 counters, therefore, the quotient is 4
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 3
For 27 ÷ 6, the quotient is 4 and the remainder is 3, or 4 r3.
Question 6.
25 ÷ 9
_____ R ______
Answer: 2 r7
Explanation:
Quotient:
A. Use 25 counters to represent the 25 dominoes. Then draw 9 circles to represent the divisor.
B. Share the counters equally among the 9 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 25 ÷ 9
D. Number of circles are equally filled with 2 counters, therefore, the quotient is 2
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 7
For 25 ÷ 7, the quotient is 2 and the remainder is 7, or 2 r7.
Question 7.
3)\(\overline { 17 } \)
_____ R ______
Answer: 5 r2
Explanation:
Quotient:
A. Use 17 counters to represent the 17 dominoes. Then draw 3 circles to represent the divisor.
B. Share the counters equally among the 3 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 17 ÷ 3
D. Number of circles are equally filled with 5 counters, therefore, the quotient is 5
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 2
For 17 ÷ 3, the quotient is 5 and the remainder is 2, or 5 r2.
Question 8.
26 ÷ 4
_____ R ______
Answer: 6 r2
Explanation:
Quotient:
A. Use 26 counters to represent the 26 dominoes. Then draw 4 circles to represent the divisor.
B. Share the counters equally among the 4 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 26 ÷ 4
D. Number of circles are equally filled with 6 counters, therefore, the quotient is 6
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 2
For 26 ÷ 4, the quotient is 6 and the remainder is 2, or 6 r2.
Divide. Draw a quick picture to help.
Question 9.
14 ÷ 3
_____ R ______
Answer: Quotient: 4 Remainder: 2




Explanation:
Quotient:
A. Use 14 counters to represent the 14 dominoes. Then draw 3 circles to represent the divisor.
B. Share the counters equally among the 3 groups by placing them in the circles.
C. Number of circles filled= quotient of 14 ÷ 3 = 4
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 2
Question 10.
5)\(\overline { 29 } \)
_____ R ______
Answer: Quotient: 5 Remainder: 4





Explanation:
Quotient:
A. Use 29 counters to represent the 29 dominoes. Then draw 5 circles to represent the divisor.
B. Share the counters equally among the 5 groups by placing them in the circles.
C. Number of circles filled= quotient of 29 ÷ 5 = 5
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 4
Problem Solving
Question 11.
What is the quotient and remainder in the division problem modeled below?
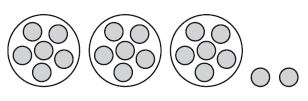
_____ R ______
Answer: quotient:6 remainder2
Explanation:
Quotient:
A. Use 20 counters to represent the 20 dominoes. Then draw 3 circles to represent the divisor.
B. Share the counters equally among the 3 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 20 ÷ 3
D. Number of circles are equally filled with 6 counters, therefore, the quotient is 6
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 2
For 20 ÷ 3, the quotient is 6 and the remainder is 2, or 6 r2.
Question 12.
Mark drew the following model and said it represented the problem 21 ÷ 4. Is Mark’s model correct? If so, what is the quotient and remainder? If not, what is the correct quotient and remainder?
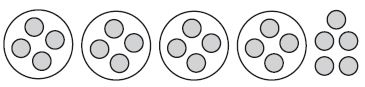
_____ ; _____ r
Answer: 4 r5
Explanation:
Quotient:
A. Use 21 counters to represent the 21 dominoes. Then draw 4 circles to represent the divisor.
B. Share the counters equally among the 4 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 21 ÷ 4
D. Number of circles are equally filled with 4 counters, therefore, the quotient is 4
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 5
For 21 ÷ 4, the quotient is 4 and the remainder is 5, or 4 r5.
Common Core – Page No. 208
Lesson Check
Question 1.
What is the quotient and remainder for 32 ÷ 6?
Options:
a. 4 r3
b. 5 r1
c. 5 r2
d. 6 r1
Answer: c. 5 r2
Explanation:
Quotient:
A. Use 32 counters to represent the 32 dominoes. Then draw 6 circles to represent the divisor.
B. Share the counters equally among the 5 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 32 ÷ 6
D. Number of circles are equally filled with 5 counters, therefore, the quotient is 5
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 2
For 32 ÷ 6, the quotient is 5 and the remainder is 2, or 5 r2.
Question 2.
What is the remainder in the division problem modeled below?
Options:
a. 8
b. 4
c. 3
d. 1
Answer: c. 3
Explanation:
When a number cannot be divided evenly, the amount left over is called the remainder.
The number of counters that are left = remainder = 3
Spiral Review
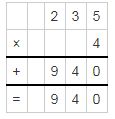
Question 3.
Each kit to build a castle contains 235 parts. How many parts are in 4 of the kits?
Options:
a. 1,020
b. 940
c. 920
d. 840
Answer: b. 940
Explanation:
Number of parts used to build a castle in each kit=235 parts
Number of kits= 4
Total number of parts in 4 of the kits= 235 x 4=940 parts
Question 4.
In 2010, the population of Alaska was about 710,200. What is this number written in word form?
Options:
a. seven hundred ten thousand, two
b. seven hundred twelve thousand
c. seventy-one thousand, two
d. seven hundred ten thousand, two hundred
Answer: d. seven hundred ten thousand, two hundred
Explanation:
The ones and tens place of the number are zeroes, so the next place which is hundreds is considered and the value is 7 so, it can be written as seven hundred and in the thousands period it can be written as seven hundred ten thousand.
Question 5.
At the theater, one section of seats has 8 rows with 12 seats in each row. In the center of the first 3 rows are 4 broken seats that cannot be used. How many seats can be used in the section?
Options:
a. 84
b. 88
c. 92
d. 96
Answer: c. 92
Explanation:
Number of rows at the theatre = 8
Number of seats each row= 12
Number of seats broken and that cannot be used to sit= 4
Total number of seats that can be used= 12 x 8-4=96-4=92
Question 6.
What partial products are shown by the model below?

Options:
a. 300, 24
b. 300, 600, 40, 60
c. 300, 60, 40, 24
d. 300, 180, 40, 24
Answer: d. 300, 180, 40, 24
Explanation:
The whole rectangle is divided into four small rectangles the areas of these rectangles are:
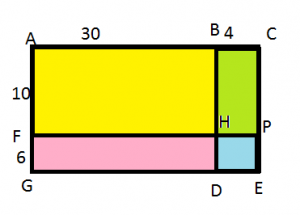
Area of yellow rectangle= 30 x 10=300
Area of green rectangle= 4 x 10 = 40
Area of pink rectangle= 6 x 30= 180
Area of blue rectangle= 4 x 6= 24
Common Core – Page No. 211
Question 1.
Olivia baked 53 mini-loaves of banana bread to be sliced for snacks at a craft fair. She will place an equal number of loaves in 6 different locations. How many loaves will be at each location?
a. Divide to find the quotient and remainder.
□ r □
6)\(\overline { 53 } \)
_____ R ______
Answer: Quotient: 8 Remainder: 5
Explanation:
Quotient:
A. Use 53 counters to represent the 53 dominoes. Then draw 6 circles to represent the divisor.
B. Share the counters equally among the 6 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 53 ÷ 6
D. Number of circles are equally filled with 8 counters, therefore, the quotient is 8
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 5

Therefore, there will be 8 loaves at each location.
Question 1.
b. Decide how to use the quotient and remainder to answer the question.
Type below:
____________
Answer:

The quotient is used to determine the number of loaves at each location, while the remainder gives us the information about the number of loaves left after placing in different locations.
Explanation:
Quotient:
A. Use 53 counters to represent the 53 dominoes. Then draw 6 circles to represent the divisor.
B. Share the counters equally among the 6 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 53 ÷ 6
D. Number of circles are equally filled with 8 counters, therefore, the quotient is 8
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 5
Therefore, there will be 8 mini loaves at each location.
Interpret the remainder to solve.
Question 2.
What if Olivia wants to put only whole loaves at each location? How many loaves will be at each location?
_______ whole loaves
Answer: Since there are 8 mini loaves at each location. Then there will be 4 whole loaves.
Explanation:
Olivia baked 53 mini-loaves of banana bread
Question 3.
Ed carves 22 small wooden animals to sell at the craft fair. He displays them in rows with 4 animals in a row. How many animals will not be in equal rows?
_______ animals
Answer: 2
Explanation:
Total number of small wooden animals=22
Number of animals in each row=4
Number of rows= 22÷4 =5
The total number of animals in the rows= 5 x 4=20
Number of animals which are not in a row= 22-20=2
Interpret the remainder to solve.
Question 4.
Myra has a 17-foot roll of crepe paper to make 8 streamers to decorate for a party. How long will each streamer be if she cuts the roll into equal pieces?
Type below:
____________
Answer: 2 foot
Explanation:
Length of the crepe paper = 17 foot
Number of streamers in the party=8
Length of each part if they are cut into equal pieces = 17 ÷ 8

Question 5.
Juan has a piano recital next month. Last week he practiced for 8 hours in the morning and 7 hours in the afternoon. Each practice session is 2 hours long. How many full practice sessions did Juan complete?
_______ full practice sessions
Answer: 7 full practice sessions
Explanation:
Number of hours he practiced in the morning= 8 hours
Each practice session is 2 hours long
Number of full practice sessions attended by Juan in the morning= 8÷2=4
Number of hours he practiced in the afternoon= 7 hours
Number of full practice sessions attended by Juan in the evening= 7÷2=3
Question 6.
A total of 25 students sign up to be hosts on Parent’s Night. Teams of 3 students greet parents. How many students cannot be on a team? Explain.
_______ student
Answer: 1 student
Explanation:
Total number of students= 25
Number of students in each group = 3
The number of students who cannot be in the group= remainder obtained when 25÷3= 1
Page No. 212
Use the picture for 7–9.

Question 7.
Teresa is making sock puppets just like the one in the picture. If she has 53 buttons, how many puppets can she make?
_______ sock puppets
Answer: 17 sock puppets
Explanation:
Total number of buttons Teresa has=53
Number of buttons each puppet needs= 3
Number of sock puppets made= Quotient of 53÷3=17 sock puppets
Question 8.
Write a question about Teresa and the sock puppets for which the answer is 3. Explain the answer.
Type below:
____________
Answer: How many buttons did Teresa use for one sock puppet?
Explanation:
Total number of sock puppets made= 17
Number of buttons used for making 17 sock puppets = 52
then,
Number of buttons used for one sock puppet= Quotient of 52÷17= 3 buttons
Question 9.
Interpret a Result How many more buttons will Teresa need if she wants to make 18 puppets? Explain.
_______ buttons
Answer: 1 button
Explanation:
After preparing 17 puppets there was 2 buttons leftover then on the addition of 1 button gives 3 buttons which can be used to prepare another puppet.
Question 10.
A total of 56 students signed up to play in a flag football league. If each team has 10 students, how many more students will need to sign up so all of the students can be on a team?
_______ students
Answer: 4 students
Explanation:
Total number of students in the football league= 56
Number of students in each group= 10
then,
Number of groups= Quotient of 56÷10=5 groups
Remainder= 6
By the addition of 4 students, the group of 6 gets completed by 10
Therefore, 4 students should be added so that all students can be on a team.
Question 11.
A teacher plans for groups of her students to eat lunch at tables. She has 34 students in her class. Each group will have 7 students. How many tables will she need? Explain how to use the quotient and remainder to answer the question.
_______ tables
Answer: She needs 3 tables
Explanation:

Quotient:
A. Use 34 counters to represent the 34 dominoes. Then draw 7 circles to represent the divisor.
B. Share the counters equally among the 7 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 34 ÷ 7
D. Number of circles are equally filled with 4 counters, therefore, the quotient is 4
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 6
The quotient is used to indicate the number of groups
Therefore, there will be 4 tables.
While the remainder is used to determine the number of students in the incomplete group.
Common Core – Page No. 213
Interpret the Remainder
Interpret the remainder to solve.
Question 1.
Hakeem has 100 tomato plants. He wants to plant them in rows of 8. How many full rows will he have?
Think: 100 ÷ 8 is 12 with a remainder of 4. The question asks “how many full rows,” so use only the quotient.
12 full rows
Answer: 12 full rows
Explanation:
Quotient:
A. Use 100 counters to represent the 100 dominoes. Then draw 8 circles to represent the divisor.
B. Share the counters equally among the 8 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 100 ÷ 8
D. Number of circles are equally filled with 12 counters, therefore, the quotient is 12
Therefore, the tomatoes placed in full rows are 12
Question 2.
A teacher has 27 students in her class. She asks the students to form as many groups of 4 as possible. How many students will not be in a group?
_______ students
Answer: 3 students will not be the group
Explanation:
Total number of students in the class= 27
Number of students who make a group=4
Number of groups that can be made =Quotient of 27÷ 4=6
Number of students who do not come under a group= Remainder of 27÷ 4=3
Question 3.
A sporting goods company can ship 6 footballs in each carton. How many cartons are needed to ship 75 footballs?
_______ cartons
Answer: 12 full cartons and 0.5 or 1/2 carton to ship all the 75 footballs
Explanation:
Total number of footballs that should be shipped= 75
Number of footballs placed in each carton = 6
Number of cartons required=Quotient of 75÷ 6=12

Since each carton carries 6 balls, half carton contains 3 balls because 6÷3=2, therefore, each half of the carton contains 3 balls.
Question 4.
A carpenter has a board that is 10 feet long. He wants to make 6 table legs that are all the same length. What is the longest each leg can be?
_______ foot
Answer: The length of the longest leg=4 foot-long
Explanation:
According to the question,
Length of the board the carpenter has= 10 foot long
Number of table legs that are to be made = 6
Length of the 6 table legs are equal
then,
Length of each table leg= Quotient of 10÷6=1 foot
Length of the longest table leg= Remainder of 10÷6= 4 foot.
Question 5.
Allie wants to arrange her flower garden in 8 equal rows. She buys 60 plants. What is the greatest number of plants she can put in each row?
_______ plants
Answer: 7
Explanation:
Total number of plants Allie bought= 60
Number of rows= 8
Number of plants in each row= Quotient of 60÷8=7
Problem Solving
Question 6.
Joanna has 70 beads. She uses 8 beads for each bracelet. She makes as many bracelets as possible. How many beads will Joanna have left over?
_______ beads
Answer: 6 beads
Explanation:
Total number of beads Joanna has= 70 beads
Number beads used for each bracelet= 8 beads
Number of bracelets made with these beads= Quotient of 70÷8= 7 bracelets
then,
The number of beads leftover= Remainder of 70÷8= 6 beads
Question 7.
A teacher wants to give 3 markers to each of her 25 students. Markers come in packages of 8. How many packages of markers will the teacher need?
_______ packages
Answer: 10 packages
Explanation:
Total number of students= 25
Number of markers each student got= 3
Total number of markers the teacher needs to distribute= 25 x 3= 75
Number of markers in each package= 8
Number of packages the teacher required= Quotient of 75÷8=9
While the remainder= 3
Therefore the total number packages=10
Common Core – Page No. 214
Lesson Check
Question 1.
Marcus sorts his 85 baseball cards into stacks of 9 cards each. How many stacks of 9 cards can Marcus make?
Options:
a. 4
b. 8
c. 9
d. 10
Answer: d. 10
Explanation:
Total number of baseball cards=85
Number of cards in each stack=9
Number of stacks sorted= Quotient of 85÷9=9
While the remainder=4
So the total number of stacks required= 10
Question 2.
A minivan can hold up to 7 people. How many minivans are needed to take 45 people to a basketball game?
Options:
a. 3
b. 5
c. 6
d. 7
Answer: d. 7
Explanation:
A minivan can hold up to 7 people.
Total number of people who want to hire the minivan= 45 people
Number of minivans required= Quotient of 45÷7= 6 vans
While the remainder is 3.
Total number of minivans required to take the people to the baseball game= 7 minivans
Spiral Review
Question 3.
Mrs. Wilkerson cut some oranges into 20 equal pieces to be shared by 6 friends. How many pieces did each person get and how many pieces were left over?
Options:
a. 2 pieces with 4 pieces leftover
b. 3 pieces with 2 pieces leftover
c. 3 pieces with 4 pieces leftover
d. 4 pieces with 2 pieces leftover
Answer: b. 3 pieces with 2 pieces leftover
Explanation:
Total number of orange pieces= 20
Number of friends= 6
Number of pieces each friend got= Quotient of 20÷6= 3 pieces
Number of pieces leftover= Remainder of 20÷6= 2 pieces
Question 4.
A school bought 32 new desks. Each desk cost $24. Which is the best estimate of how much the school spent on the new desks?
Options:
a. $500
b. $750
c. $1,000
d. $1,200
Answer: b. $750
Explanation:
Total number of desks= 32
Cost of each desk= $24
Total cost spent on the desks= 32 x 24=$768
So the estimated value can be $768
Question 5.
Kris has a box of 8 crayons. Sylvia’s box has 6 times as many crayons as Kris’s box. How many crayons are in Sylvia’s box?
Options:
a. 48
b. 42
c. 36
d. 4
Answer: 48 crayons
Explanation:
Number of crayons in Kris box=8
Number of crayons in Sylvia’s box= 6 times as many crayons as Kris’s box= 6 x 8=48
Question 6.
Yesterday, 1,743 people visited the fair. Today, there are 576 more people at the fair than yesterday. How many people are at the fair today?
Options:
a. 1,167
b. 2,219
c. 2,319
d. 2,367
Answer: c. 2,319
Explanation:
Number of people in the fair yesterday= 1,743
Number of more people at the fair than yesterday= 576
Total number of people in the fair today=2,319
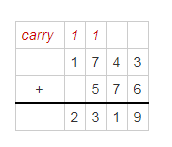
Page No. 216
Question 1.
Divide. 2,800 ÷ 7
What basic fact can you use? ___________
2,800 = 28 ___________
28 hundreds ÷ 7 = ___________
2,800 ÷ 7 = ___________
Type below:
___________
Answer: 400
Explanation:
STEP 1 Identify the basic fact. 28 ÷ 7
STEP 2 Use place value. 2,800 = 28 hundreds
STEP 3 Divide. 28 hundreds ÷ 4 = 4 hundreds
2,800 ÷ 7 = 400
Question 2.
Divide. 280 ÷ 7
What basic fact can you use? ___________
280 = 28 ___________
28 tens ÷ _____ = 4 ___________
280 ÷ 7 = _____
Type below:
___________
Answer: 40
Explanation:
STEP 1 Identify the basic fact. 28 ÷ 7
STEP 2 Use place value. 280 = 28 tens
STEP 3 Divide. 28 tens ÷ 4 = 4 tens
280 ÷ 7 = 40
Use basic facts and place value to find the quotient.
Question 3.
360 ÷ 6 = ______
Answer: 60
Explanation:
STEP 1 Identify the basic fact. 36 ÷ 6
STEP 2 Use place value. 360 = 36 tens
STEP 3 Divide. 36 tens ÷6 = 6 tens
360 ÷ 6 = 60
Question 4.
2,000 ÷ 5 = ______
Answer: 400
Explanation:
STEP 1 Identify the basic fact. 20 ÷ 5
STEP 2 Use place value. 2,000 = 20 hundreds
STEP 3 Divide. 20 hundreds ÷ 5 = 4 hundreds
2,000 ÷ 5 = 400
Question 5.
4,500 ÷ 9 = ______
Answer: 500
Explanation:
STEP 1 Identify the basic fact. 45 ÷ 9
STEP 2 Use place value. 4,500 = 45 hundreds
STEP 3 Divide. 45 hundreds ÷ 9 = 5 hundreds
4,500 ÷ 9 = 500
Question 6.
560 ÷ 8 = ______
Answer: 70
Explanation:
STEP 1 Identify the basic fact. 56 ÷ 8
STEP 2 Use place value. 560 = 56 tens
STEP 3 Divide. 56 tens ÷ 8 = 7 tens
560 ÷ 8 = 70
Question 7.
6,400 ÷ 8 = ______
Answer: 800
Explanation:
STEP 1 Identify the basic fact. 64 ÷ 8
STEP 2 Use place value. 6,400 =64 hundreds
STEP 3 Divide. 64 hundreds ÷ 8 = 8 hundreds
6,400 ÷ 8 = 800
Question 8.
3,500 ÷ 7 = ______
Answer:
Explanation:
STEP 1 Identify the basic fact. 35 ÷ 7
STEP 2 Use place value. 3,500 = 35 hundreds
STEP 3 Divide. 35 hundreds ÷ 7 = 5 hundreds
3,500 ÷ 7 = 500
Use Patterns Algebra Find the unknown number.
Question 9.
420 ÷ ______ = 60
Answer: 7
Explanation:
To find the divisor (the missing number) divide 420 with 60

Therefore the quotient of 420 ÷ 60= The missing number=7
Question 10.
______ ÷ 4 = 30
Answer: 120
Explanation:
To find the dividend (the missing number) we must multiply the divisor and the quotient.
Therefore the dividend is 30 x 4=120.
Question 11.
810 ÷ ______ = 90
Answer: 9
Explanation:
To find the divisor (the missing number) divide 810 with 90

Therefore the quotient of 810 ÷ 90= The missing number=9
Question 12.
Divide 400 ÷ 40. Explain how patterns and place value can help.
______
Answer: 10
Explanation:
STEP 1 Identify the basic fact. 40 ÷ 4
STEP 2 Use place value. 400 = 40 tens
STEP 3 Divide. 40 tens ÷ 4 = 1 tens
400 ÷ 40 = 10
Question 13.
Eileen collected 98 empty cans to recycle, and Carl collected 82 cans. They packed an equal number of cans into each of three boxes to take to the recycling center.
How many cans were in each box?
______ cans
Answer: 60 cans
Explanation:
Total number of cans = 98+82=180 cans
Number of boxes= 3
Number of cans in each box= 180 ÷3=60 cans
Question 14.
It costs a baker $18 to make a small cake. He sells 8 small cakes for $240. How much more is the selling price of each cake than the cost?
$ ______
Answer: $96
Explanation:
Cost of each cake= $18
Number of cakes baked= 8
The actual cost of the cakes = $18 x $8=$144
The selling price of the cakes=$240
Amount gained on the cakes= $240-$144=$96
Page No. 217
Question 15.
Jamal put 600 pennies into 6 equal rolls. How many pennies were in each roll?

______ pennies
Answer: 100 pennies
Explanation:
Total number of pennies= 600
Number of rolls= 6
The number of pennies= Quotient of 600 ÷ 6=100
Question 16.
Sela has 6 times as many coins now as she had 4 months ago. If Sela has 240 coins now, how many coins did she have 4 months ago?
______ coins
Answer: 60 coins
Explanation:
Let the number of coins four months ago be x coins.
According to the question,
Number of coins Sela has at present = 4x
4x=240
x= 240 ÷ 4=60
Therefore the number of coins Sela has=60
Question 17.
Chip collected 2,090 dimes. Sue collected 1,910 dimes. They divided all their dimes into 8 equal stacks. How many dimes are in each stack?
______ dimes
Answer:
Explanation:
Number of dimes Chip collected= 2,090
Number of dimes Sue collected= 1,910
Total number of dimes= 2,090+1,910= 4100
Number of stacks= 8
Number of dimes in each stack = Quotient of 4100 ÷8=512
Question 18.
Communicate Mr. Roberts sees a rare 1937 penny. The cost of the penny is $210. If he saves $3 each week, will Mr. Roberts have enough money to buy the penny in one year? Explain.
______
Answer: No Mr. Roberts cannot buy the penny in one year.
Explanation:
Amount saved in each week= $3
Number of weeks in a year= 52
The total amount saved= 52 x 3=$156
Cost of the penny=$210
Therefore Mr. Roberts cannot buy the penny in one year.
Question 19.
Mrs. Fletcher bought 5 coins for $32 each. Later, she sold all the coins for $300. How much more did Mrs. Fletcher receive for each coin than she paid? Explain.
$ ______
Answer:$60
Explanation:
Number of coins=5
Cost of each coin = $32
Total cost of the coins= $32 x 5=$160
She sold the coins for $300
Cost of each coin= $300 ÷ 5= $60
Page No. 218
Question 20.
Which quotients are equal to 20? Mark all that apply.
Options:
a. 600 ÷ 2
b. 1,200 ÷ 6
c. 180 ÷ 9
d. 140 ÷ 7
e. 500 ÷ 5
Answer: c. 180 ÷ 9
d. 140 ÷ 7
Explanation:
Quotient:
A. Use 180 counters to represent the 180 dominoes. Then draw 9 circles to represent the divisor.
B. Share the counters equally among the 9 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 180 ÷ 9
D. Number of circles are equally filled with 20 counters, therefore, the quotient is 20
Quotient:
A. Use 140 counters to represent the 140 dominoes. Then draw 7 circles to represent the divisor.
B. Share the counters equally among the 7 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 140 ÷ 7
D. Number of circles are equally filled with 20 counters, therefore, the quotient is 20
Insect Flight
True flight is shared only by insects, bats, and birds. Flight in insects varies from the clumsy flight of some beetles to the acrobatic moves of dragonflies.
The wings of insects are not moved by muscles attached to the wings. Muscles in the middle part of the body, or thorax, move the wings. The thorax changes shape as the wings move.

Question 21.
About how many times does a damselfly’s wings beat in 1 minute?
______ times
Answer: 900
Explanation:
Total number of wingbeats of Damselfly in 3 minutes= 2,700
Number of wingbeats of Damselfly in 1 minute= 2,700 ÷3=900
Question 22.
About how many times do a scorpion fly’s wings beat in 6 minutes?
______ times
Answer: 10,000
Explanation:
Total number of wingbeats of scorpionfly in 3 minutes=5,000
Number of parts of time-intervals in 6 minutes = 6÷3=2
Number of wingbeats of scorpionfly in 6 minutes= 5,000 x 2 = 10,000
Question 23.
In one minute, about how many more times do a damselfly’s wings beat than a large white butterfly’s wings?
______ more times
Answer: 200
Explanation:
Total number of wingbeats of Damselfly in 3 minutes= 2,700
Number of wingbeats of Damselfly in 1 minute= 2,700 ÷3=900
Total number of wingbeats of large white butterfly in 3 minutes= 2,100
Number of wingbeats of large white butterfly in 1 minute= 2,100 ÷3=700
Number of more times the damselfly’s wings beat than a large white butterfly=900-700=200
Question 24.
What’s the Question? The answer is about 2,300 times.
Type below:
___________
Answer: About how many times do an Aeschind dragonfly’s wings beat in 1 minute?
Explanation:
Total number of wingbeats of Aeschind dragonfly’s in 3 minutes= 6,900
Number of wingbeats of Aeschind dragonfly’s in 1 minute= 6,900 ÷3=2,300
Common Core – Page No. 219
Divide Tens, Hundreds, and Thousands
Use basic facts and place value to find the quotient.
Question 1.
3,600 ÷ 4 = 900
Think: 3,600 is 36 hundreds.
Use the basic fact 36 ÷ 4 = 9.
So, 36 hundreds ÷ 4 = 9 hundreds, or 900.
Answer: 900
Explanation:
STEP 1 Identify the basic fact. 36 ÷ 4
STEP 2 Use place value. 3,600 = 36 hundreds
STEP 3 Divide. 36 hundered ÷ 4 = 9 hundreds
3,600 ÷ 4 = 900
Question 2.
240 ÷ 6 = ______
Answer: 40
Explanation:
STEP 1 Identify the basic fact. 24 ÷ 6
STEP 2 Use place value. 240 = 24 tens
STEP 3 Divide. 24 tens ÷ 6 = 4 tens
240 ÷ 6 = 40
Question 3.
5,400 ÷ 9 = ______
Answer: 600
Explanation:
STEP 1 Identify the basic fact. 54 ÷ 9
STEP 2 Use place value. 5,400 = 54 hundreds
STEP 3 Divide. 54 hundreds ÷ 9 = 6 hundreds
5,400 ÷ 9 = 600
Question 4.
300 ÷ 5 = ______
Answer: 60
Explanation:
STEP 1 Identify the basic fact. 30 ÷ 5
STEP 2 Use place value. 300 = 30 tens
STEP 3 Divide. 30 tens ÷ 5 = 60 tens
300 ÷ 5 = 60
Question 5.
4,800 ÷ 6 = ______
Answer: 800
Explanation:
STEP 1 Identify the basic fact. 48 ÷ 6
STEP 2 Use place value. 4,800 = 48 hundreds
STEP 3 Divide. 48 hundreds ÷ 6 = 80 hundreds
4,800 ÷ 6 = 800
Question 6.
420 ÷ 7 = ______
Answer: 60
Explanation:
STEP 1 Identify the basic fact. 42 ÷ 7
STEP 2 Use place value. 420 = 42 tens
STEP 3 Divide. 42 tens ÷ 7 = 60 tens
420 ÷ 7 = 60
Question 7.
150 ÷ 3 = ______
Answer: 50
Explanation:
STEP 1 Identify the basic fact. 15 ÷ 3
STEP 2 Use place value. 150 = 15 tens
STEP 3 Divide. 15 tens ÷ 3 = 5 tens
150 ÷ 3 = 50
Question 8.
6,300 ÷ 7 = ______
Answer: 900
Explanation:
STEP 1 Identify the basic fact. 63 ÷ 7
STEP 2 Use place value. 6,300 = 63 hundreds
STEP 3 Divide. 63 hundreds ÷ 7 = 9 hundreds
6,300 ÷ 7 = 900
Question 9.
1,200 ÷ 4 = ______
Answer: 300
Explanation:
STEP 1 Identify the basic fact. 12 ÷ 4
STEP 2 Use place value. 1,200 = 12 hundreds
STEP 3 Divide. 12 hundreds ÷ 4 = 3 hundreds
1,200 ÷ 4 = 300
Question 10.
360 ÷ 6 = ______
Answer: 60
Explanation:
STEP 1 Identify the basic fact. 36 ÷ 6
STEP 2 Use place value. 360 = 36 tens
STEP 3 Divide. 36 tens ÷ 6 = 6 tens
360 ÷ 6 = 60
Find the quotient.
Question 11.
28 ÷ 4 = ______
280 ÷ 4 = ______
2,800 ÷ 4 = ______
Answer: 7, 70, 700
Explanation:
Quotient:
A. Use 28 counters to represent the 28 dominoes. Then draw 4 circles to represent the divisor.
B. Share the counters equally among the 4 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 28 ÷ 4
D. Number of circles are equally filled with 7 counters, therefore, the quotient is 7
STEP 1 Identify the basic fact. 28 ÷ 4
STEP 2 Use place value. 280 = 28 tens
STEP 3 Divide. 28 tens ÷ 4 = 7 tens
280 ÷ 4 = 70
STEP 1 Identify the basic fact. 28 ÷ 4
STEP 2 Use place value. 2,800 = 28 hundreds
STEP 3 Divide. 28 hundreds ÷ 4 = 7 hundreds
2,800 ÷ 4 = 700
Question 12.
18 ÷ 3 = ______
180 ÷ 3 = ______
1,800 ÷ 3 = ______
Answer: 6, 60, 600
Explanation:
Quotient:
A. Use 18 counters to represent the 18 dominoes. Then draw 3 circles to represent the divisor.
B. Share the counters equally among the 3 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 18 ÷ 3
D. Number of circles are equally filled with 6 counters, therefore, the quotient is 6
STEP 1 Identify the basic fact. 18 ÷ 3
STEP 2 Use place value. 180 = 18 tens
STEP 3 Divide. 18 tens ÷ 3 = 6 tens
180 ÷ 6 = 60
STEP 1 Identify the basic fact. 18 ÷ 3
STEP 2 Use place value. 1,800 = 18 hundreds
STEP 3 Divide. 18 hundreds ÷ 3 = 6 hundreds
1,800 ÷ 3 = 600
Question 13.
45 ÷ 9 = ______
450 ÷ 9 = ______
4,500 ÷ 9 = ______
Answer: 5, 50, 500
Explanation:
Quotient:
A. Use 45 counters to represent the 45 dominoes. Then draw 9 circles to represent the divisor.
B. Share the counters equally among the 9 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 45 ÷ 9
D. Number of circles are equally filled with 5 counters, therefore, the quotient is 5
STEP 1 Identify the basic fact. 45 ÷ 9
STEP 2 Use place value. 450 = 45 tens
STEP 3 Divide. 45 tens ÷ 9 = 5 tens
450 ÷ 9 = 50
STEP 1 Identify the basic fact. 45 ÷ 9
STEP 2 Use place value. 4,500 = 45 hundreds
STEP 3 Divide. 45 hundreds ÷ 9 = 5 hundreds
4,500 ÷ 9 = 500
Problem Solving
Question 14.
At an assembly, 180 students sit in 9 equal rows. How many students sit in each row?
______ students
Answer: 20
Explanation:
Total number of students= 180
Number of rows= 9
Number of students in each row= 180 ÷9=20
Question 15.
Hilary can read 560 words in 7 minutes. How many words can Hilary read in 1 minute?
______ words
Answer: 80
Explanation:
Total number of words Hilary can read in 7 minutes = 560
Number of words Hilary can read in 1 minute= 560 ÷ 7= 80
Question 16.
A company produces 7,200 gallons of bottled water each day. The company puts 8 one-gallon bottles in each carton. How many cartons are needed to hold all the one-gallon bottles produced in one day?
______ cartons
Answer: 900
Explanation:
Total number of gallons bottled in each day= 7,200
Number of gallons bottled in each carton= 8
Number of cartons used= 7,200 ÷ 8= 900
Question 17.
An airplane flew 2,400 miles in 4 hours. If the plane flew the same number of miles each hour, how many miles did it fly in 1 hour?
______ miles
Answer: 600
Explanation:
Total number of miles flew in 4 hours= 2,400
Number of miles flew in 1 hour= 2,400÷4=600
Common Core – Page No. 220
Lesson Check
Question 1.
A baseball player hits a ball 360 feet to the outfield. It takes the ball 4 seconds to travel this distance. How many feet does the ball travel in 1 second?
Options:
a. 9 feet
b. 40 feet
c. 90 feet
d. 900 feet
Answer: c. 90 feet
Explanation:
The height to which the player hits a ball=360 feet
Height to which the ball travels in 1 second= 360÷4= 90 feet
Question 2.
Sebastian rides his bike 2,000 meters in 5 minutes. How many meters does he bike in 1 minute?
Options:
a. 4 meters
b. 40 meters
c. 50 meters
d. 400 meters
Answer: d. 400 meters
Explanation:
Total number of meters travelled in 5 minutes= 2,000
Number of meters travelled in 1 minute= 2,000÷5= 400
Spiral Review
Question 3.
A full container of juice holds 63 ounces. How many 7-ounce servings of juice are in a full container?
Options:
a. 1
b. 8
c. 9
d. 10
Answer: c. 9
Explanation:
A full container of juice holds= 63 ounces
Quantity of servings of juice in one glass=7 ounce
Number of servings of the juice are= 63÷7=9
Question 4.
Paolo pays $244 for 5 identical calculators. Which is the best estimate of how much Paolo pays for one calculator?
Options:
a. $40
b. $50
c. $60
d. $245
Answer: b. $50
Explanation:
Amount Paolo pays for the identical calculators = $244
Number of identical calculators=5
The best estimated value of each identical calculator=$244 ÷ 5is approximately $50
Question 5.
A football team paid $28 per jersey. They bought 16 jerseys. How much money did the team spend on jerseys?
Options:
a. $44
b. $196
c. $408
d. $448
Answer: d. $448
Explanation:
Cost of each jersey=$28
Number of jerseys= 16
Total cost of the jerseys= $28 x 16= $448
Question 6.
Suzanne bought 50 apples at the apple orchard. She bought 4 times as many red apples as green apples. How many more red apples than green apples did Suzanne buy?
Options:
a. 10
b. 25
c. 30
d. 40
Answer: d. 40
Explanation:
Let the number of green apples be x and the number of red apples be 4x
4x + x = 50
x = 50 ÷ 5= 10
Number of red balls = 4x = 4 x 10 = 40
Page No. 222
Question 1.
Estimate. 1,718 ÷ 4
Think: What number close to 1,718 is easy to divide by 4?
______ is close to 1,718. What basic fact can you use?
______ ÷ 4
______ is close to 1,718. What basic fact can you use?
______ ÷ 4
Choose 1,600 because
__________________________________.
16 ÷ 4 = ______
1,600 ÷ ______ = ______
1,718 ÷ 4 is about ______
Type below:
_________
Answer:
Explanation:
What number close to 1,718 is easy to divide by 4?
1,600 is close to 1,718. What basic fact can you use?
1,600 ÷ 4
Choose 1,600 because it is close to 1,718 and can easily be divided by 4.
16 ÷ 4 = 4
1,600 ÷ 4 = 400
1,600 ÷ 4 is about 400
Use compatible numbers to estimate the quotient.
Question 2.
455 ÷ 9
______
Answer: 50
Explanation:
What number close to 455 is easy to divide by 9?
450 is close to 455. What basic fact can you use?
450 ÷ 9
Choose 450 because it is close to 455 and can easily be divided by 9.
45 ÷ 9 = 5
450 ÷ 9 = 50
455 ÷ 9 is about 50
Question 3.
1,509 ÷ 3
______
Answer: 500
Explanation:
What number close to 1,509 is easy to divide by 3?
1,500 is close to 1,509. What basic fact can you use?
1,500 ÷ 3
Choose 1,500 because it is close to 1,509 and can easily be divided by 3.
15 ÷ 3 = 5
1,500 ÷ 3 = 500
1,509 ÷ 3 is about 500
Question 4.
176 ÷ 8
______
Answer:
Explanation:
What number close to 176 is easy to divide by 8?
160 is close to 176. What basic fact can you use?
160 ÷ 8
Choose 160 because it is close to 176 and can easily be divided by 8.
16 ÷ 8 = 2
160 ÷ 8 = 20
176 ÷ 8 is about 20
Question 5.
2,795 ÷ 7
______
Answer: 400
Explanation:
What number close to 2,795 is easy to divide by 7?
2,800 is close to 2,795. What basic fact can you use?
2,800 ÷ 7
Choose 2,800 because it is close to 2,795 and can easily be divided by 7.
28 ÷ 7 = 4
2,800 ÷ 7 = 400
2,795 ÷ 7 is about 400
Use compatible numbers to find two estimates that the quotient is between.
Question 6.
5,321 ÷ 6
______ and ______
Answer: 900
Explanation:
What number close to 5,321 is easy to divide by 6?
5,400 is close to 5,321. What basic fact can you use?
5,400 ÷ 6
Choose 5,400 because it is close to 5,321 and can easily be divided by 6.
54 ÷ 6 = 9
5,400 ÷ 6 = 900
5,321 ÷ 6 is about 900
Question 7.
1,765 ÷ 6
______ and ______
Answer: 300
Explanation:
What number close to 1,765 is easy to divide by 6?
1,800 is close to 1,765. What basic fact can you use?
1,800 ÷ 6
Choose 1,800 because it is close to 1,765 and can easily be divided by 6.
18 ÷ 6 = 3
1,800 ÷ 6 = 300
1,765 ÷ 6 is about 300
Question 8.
1,189 ÷ 3
______ and ______
Answer: 400
Explanation:
What number close to 1,189 is easy to divide by 3?
1,200 is close to 1,189. What basic fact can you use?
1,200 ÷ 3
Choose 1,200 because it is close to 1,189 and can easily be divided by 3.
12 ÷ 3 = 4
1,200 ÷ 3 = 400
1,189 ÷ 3 is about 400
Question 9.
2,110 ÷ 4
______ and ______
Answer: 500
Explanation:
What number close to 2,110 is easy to divide by 4?
2,000 is close to 2,110. What basic fact can you use?
2,000 ÷ 4
Choose 2,000 because it is close to 2,110 and can easily be divided by 4.
20 ÷ 4 = 5
2,000 ÷ 4 = 500
2,110 ÷ 4 is about 500
Reason Abstractly Algebra Estimate to compare. Write <, >, or =.
Question 10.
613 ÷ 3 ______ 581 ÷ 2
Answer: 613 ÷ 3 < 581 ÷ 2
Explanation:
What number close to 613 is easy to divide by 3?
600 is close to 613. What basic fact can you use?
600 ÷ 3
Choose 600 because it is close to 613 and can easily be divided by 3.
6 ÷ 3 = 2
600 ÷ 3 = 200
613 ÷ 3 is about 200
What number close to 581 is easy to divide by 2?
580 is close to 581. What basic fact can you use?
580 ÷ 2
Choose 580 because it is close to 581 and can easily be divided by 2.
58 ÷ 2 = 29
580 ÷ 2 = 290
581 ÷ 2 is about 290
Question 11.
364 ÷ 4 ______ 117 ÷ 6
Answer: 364 ÷ 4 > 117 ÷ 6
Explanation:
What number close to 364 is easy to divide by 4?
360 is close to 364. What basic fact can you use?
360 ÷ 4
Choose 360 because it is close to 364 and can easily be divided by 4.
36 ÷ 4 = 9
360 ÷ 4 = 90
364 ÷ 4 is about 90
What number close to 117 is easy to divide by 6?
120 is close to 117. What basic fact can you use?
120 ÷ 6
Choose 120 because it is close to 117 and can easily be divided by 6.
12 ÷ 6 = 2
120 ÷ 6 = 20
117 ÷ 6 is about 20
Question 12.
2,718 ÷ 8 ______ 963 ÷ 2
Answer: 2,718 ÷ 8 < 963 ÷ 2
Explanation:
What number close to 2,718 is easy to divide by 8?
2,400 is close to 2,718. What basic fact can you use?
2,400 ÷ 8
Choose 2,400 because it is close to 2,718 and can easily be divided by 8.
24 ÷ 8 = 3
2,400 ÷ 8 = 300
2,718 ÷ 8 is about 300
What number close to 963 is easy to divide by 2?
960 is close to 963. What basic fact can you use?
960 ÷ 2
Choose 960 because it is close to 963 and can easily be divided by 2.
96 ÷ 2 = 48
960 ÷ 2 = 480
963 ÷ 2 is about 480
Question 13.
If Cade shoots 275 free throw baskets in 2 hours, about how many can he shoot in 5 hours?
about ______ free throw baskets
Answer: 688 free throw baskets
Explanation:
Number of free-throw baskets in 2 hours= 275
Number of free-throw baskets in 1 hour = 275÷2=137.5
Number of free-throw baskets in 5 hours= 137.5 x 5= 687.5 =rounding to nearest whole number 688 free throw baskets ( approx)
Question 14.
A carpenter has 166 doorknobs in his workshop. Of those doorknobs, 98 are round and the rest are square. If he wants to place 7 square doorknobs in each bin, about how many bins would he need?
about ______ bins
Answer: 10
Explanation:
The total number of doorknobs in a workshop= 166
Number of round doorknobs in a workshop= 98
Number of square doorknobs in a workshop=166-98=68
Number of square doorknobs in each bin= 7
Number of bins= 68÷7= 9.7= rounding to nearest whole number 10 bins (approx)
Page No. 223
Use the table for 15–17.
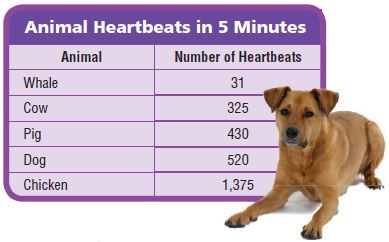
Question 15.
About how many times does a chicken’s heart beat in 1 minute?
about ______ times
Answer: 275
Explanation:
Number of times the chicken’s heartbeats in 5 minutes= 1,375
Number of times the chicken’s heartbeats in 1 minute= 1,375÷ 5= 275
Question 16.
About how many times does a cow’s heart beat in 2 minutes?
about ______ times
Answer: 130
Explanation:
Number of times the cow’s heartbeats in 5 minutes= 325
Number of times the cow’s heartbeats in 1 minute= 325÷5=65
Number of times the cow’s heartbeats in 2 minutes= 65 x 2=130
Question 17.
Use Reasoning About how many times faster does a cow’s heart beat than a whale’s?
about ______ times
Answer: nearly 11 times
Explanation:
Number of times the cow’s heartbeats in 5 minutes= 325
Number of times the cow’s heartbeats in 1 minute= 325÷5=65
Number of times the whale’s heartbeats in 5 minutes= 31
Number of times the whale’s heartbeats in 1 minute= 31÷5=6.2= rounding to nearest whole number 6 (approx)
Number of more times the cow’s heartbeats compared to whale’s=65÷6=10.8 times=rounding to a nearest whole number 11(approx)
Question 18.
Martha had 154 stamps and her sister had 248 stamps. They combined their collections and put the stamps in an album. If they want to put 8 stamps on each page, about how many pages would they need?
about ______ times
Answer: 50.25 pages
Explanation:
Number of stamps Martha has= 154
Number of stamps Martha’s sister has= 248
The total number of stamps they have= 154+248=402
Number of stamps on each page= 8
Number of pages= 402÷8= 50.25 pages= 51 (approx)
Question 19.
Jamie and his two brothers divided a package of 125 toy cars equally. About how many cars did each of them receive?
about ______ times
Answer: 41.67
Explanation:
Number of toys Jamie has= 125 toy cars
Number of toys Jamie and his two brothers divide= 125÷3= 41.67
Question 20.
Harold and his brother collected 2,019 cans over a 1-year period. Each boy collected the same number of cans. About how many cans did each boy collect? Explain how you found your answer.
about ______ times
Answer: 1,010
Explanation:
Number of cans Harold and his brother collected = 2,019 cans
Number of cans each boy collected = 2,019÷2= 1,009.5 cans = 1,010 cans(approx)
Page No. 224
Question 21.
Cause and Effect
The reading skill cause and effect can help you understand how one detail in a problem is related to another detail.

Chet wants to buy a new bike that costs $276. Chet mows his neighbor’s lawn for $15 each week. Since Chet does not have money saved, he needs to decide which layaway plan he can afford to buy the new bike.
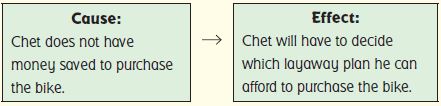
Which plan should Chet choose?
3-month layaway:
$276 ÷ 3
Estimate.
$270 ÷ 3 ______
6-month layaway:
$276 ÷ 6
Estimate.
$300 ÷ 6 _____
Chet earns $15 each week. Since there are usually 4 weeks in a month, multiply to see which payment he can afford.
$15 × 4 = _______
So, Chet can afford the ______ layaway plan.
Type below:
___________
Answer: Chet can afford the 3-months layaway plan.
Explanation:
What number close to $276 is easy to divide by 3?
$270 is close to $276. What basic fact can you use?
$270 ÷ 3
Choose 270 because it is close to 276 and can easily be divided by 3.
27 ÷ 3 = 9
270 ÷ 3 = 90
$276 ÷ 3 is about 90
Use estimation to solve.
Question 21.
Sofia wants to buy a new bike that costs $214. Sofia helps her grandmother with chores each week for $18. Estimate to find which layaway plan Sofia should choose and why.
Type below:
___________
Answer: 3 months
Explanation:
What number close to $214 is easy to divide by 3?
$215 is close to $214. What basic fact can you use?
$215 ÷ 3
Choose 215 because it is close to 214 and can easily be divided by 3.
215 ÷ 3 = 71.6=72 (approx)
$214 ÷ 3 is about 72
Question 22.
Describe a situation when you have used cause and effect to help you solve a math problem.
Type below:
___________
Answer: To buy a bike
Explanation:
3-month layaway:
$276 ÷ 3
Estimate.
$270 ÷ 3 ______
6-month layaway:
$276 ÷ 6
Estimate.
$300 ÷ 6 _____
Chet earns $15 each week. Since there are usually 4 weeks in a month, multiply to see which payment he can afford.
$15 × 4 = _______
So, Chet can afford the ______ layaway plan.
The above is a profit gaining plan to buy a bike.
Common Core – Page No. 224
Estimate Quotients Using Compatible Numbers
Use compatible numbers to estimate the quotient.
Question 1.
389 ÷ 4
400 ÷ 4 = 100
Answer: 100
Explanation:
What number close to 389 is easy to divide by 4?
400 is close to 389. What basic fact can you use?
400 ÷ 4
Choose 400 because it is close to 389 and can easily be divided by 4.
40 ÷ 4 = 10
400 ÷ 4 = 100
389 ÷ 4 is about 100
Question 2.
358 ÷ 3
_____ ÷ 3 = _____
Answer: 120
Explanation:
What number close to358 is easy to divide by 3?
360 is close to 358. What basic fact can you use?
360 ÷ 3
Choose 360 because it is close to 358 and can easily be divided by 3.
36 ÷3 = 12
360 ÷ 3 =120
358 ÷ 3 is about 120
Question 3.
784 ÷ 8
_____ ÷ 8 = _____
Answer: 100
Explanation:
What number close to 784 is easy to divide by 8?
800 is close to 784. What basic fact can you use?
800 ÷ 8
Choose 800 because it is close to 784 and can easily be divided by 8.
80 ÷ 8 = 10
800 ÷ 8 = 100
784 ÷ 8 is about 100
Question 4.
179 ÷ 9
_____ ÷ 9 = _____
Answer: 20
Explanation:
What number close to 179 is easy to divide by 9?
180 is close to 179. What basic fact can you use?
180 ÷ 9
Choose 180 because it is close to 179 and can easily be divided by 9.
18 ÷ 9 = 2
180 ÷ 9 = 20
179 ÷ 9 is about 20
Question 5.
315 ÷ 8
_____ ÷ 8 = _____
Answer: 40
Explanation:
What number close to 315 is easy to divide by 8?
320 is close to 315. What basic fact can you use?
320 ÷ 8
Choose 320 because it is close to 315 and can easily be divided by 8.
32 ÷ 8 = 4
320 ÷ 8 =40
315 ÷ 8 is about 40
Question 6.
2,116 ÷ 7
_____ ÷ 7 = _____
Answer: 300
Explanation:
What number close to 2,116 is easy to divide by 7?
2,100 is close to 2,116. What basic fact can you use?
2,100 ÷ 7
Choose 2,100 because it is close to 2,116 and can easily be divided by 7.
21 ÷ 7= 3
2,100 ÷ 7 = 300
2,116 ÷ 7 is about 300
Question 7.
4,156 ÷ 7
_____ ÷ 7 = _____
Answer: 600
Explanation:
What number close to 4,156 is easy to divide by 7?
4,200 is close to 4,156. What basic fact can you use?
4,200 ÷7
Choose 4,200 because it is close to 4,156 and can easily be divided by 7.
42 ÷ 7 = 6
4,200 ÷ 7 = 600
4,156 ÷ 7 is about 600
Question 8.
474 ÷ 9
_____ ÷ 9 = _____
Answer: 50
Explanation:
What number close to 474 is easy to divide by 9?
450 is close to 474. What basic fact can you use?
450 ÷ 9
Choose 450 because it is close to 474 and can easily be divided by 9.
45 ÷ 9 = 5
450 ÷ 9 = 50
474 ÷ 9 is about 50
Use compatible numbers to find two estimates that the quotient is between.
Question 9.
1,624 ÷ 3
_____ ÷ 3 = _____
_____ ÷ 3 = _____
Answer: The quotient is between 500 and 600
Explanation:
What number close to 1,624 is easy to divide by 3?
1,500 is close to 1,624. What basic fact can you use?
1,500 ÷ 3
Choose 1,500 because it is close to 1,624 and can easily be divided by 3.
15 ÷ 3 = 5
1,500 ÷ 3 = 500
1,624 ÷ 3 is about 500
What number close to 1,624 is easy to divide by 3?
1,800 is close to 1,624. What basic fact can you use?
1,800 ÷ 3
Choose 1,800 because it is close to 1,624 and can easily be divided by 3.
18 ÷ 3 = 6
1,800 ÷ 3 = 600
1,624 ÷ 3 is about 600
Question 10.
2,593 ÷ 6
_____ ÷ 6 = _____
_____ ÷ 6 = _____
Answer: The quotient is between 400 and 500
Explanation:
What number close to 2,593 is easy to divide by 6?
2,400 is close to 2,593. What basic fact can you use?
2,400 ÷ 6
Choose 2,400 because it is close to 2,593 and can easily be divided by 6.
24 ÷ 6 = 4
2,400 ÷ 6 = 400
2,593 ÷ 6 is about 400
What number close to 2,593 is easy to divide by 6?
3,000 is close to 2,593. What basic fact can you use?
3000 ÷ 6
Choose 3,000 because it is close to 2,593 and can easily be divided by 6.
30 ÷ 6 = 5
3,000 ÷ 6 = 500
2,593 ÷ 6 is about 500
Question 11.
1,045 ÷ 2
_____ ÷ 2 = _____
_____ ÷ 2 = _____
Answer: The quotient is between 520 and 525
Explanation:
What number close to 1,045 is easy to divide by 2?
1,040 is close to 1,045. What basic fact can you use?
1,040 ÷ 2
Choose 1,040 because it is close to 1,045 and can easily be divided by 2.
1,04 ÷ 2 = 52
1,040 ÷ 2 = 520
1,045 ÷ 2 is about 520
What number close to 1,045 is easy to divide by 2?
1,050 is close to 1,045. What basic fact can you use?
1,050 ÷ 2
Choose 1,050 because it is close to 1,045 and can easily be divided by 2.
1,050 ÷ 2 = 525
1,045 ÷ 2 is about 525
Question 12.
1,754 ÷ 9
_____ ÷ 9 = _____
_____ ÷ 9 = _____
Answer: The quotient is between 195 and 200
Explanation:
What number close to 1,754 is easy to divide by 9?
1,755 is close to 1,754. What basic fact can you use?
1,755 ÷ 9
Choose 1,755 because it is close to 1,754 and can easily be divided by 9.
1,755 ÷ 9 = 195
1,754 ÷ 9 is about 195
What number close to 1,754 is easy to divide by 9?
1,800 is close to 1,754. What basic fact can you use?
1,800 ÷ 9
Choose 1,800 because it is close to 1,754 and can easily be divided by 9.
18 ÷ 9 = 2
1,800 ÷ 9 = 200
1,754 ÷ 9 is about 200
Question 13.
2,363 ÷ 8
_____ ÷ 8 = _____
_____ ÷ 8 = _____
Answer: The quotient is between 295 and 300
Explanation:
What number close to 2,363 is easy to divide by 8?
2,360 is close to 2,363. What basic fact can you use?
2,360 ÷ 8
Choose 2,360 because it is close to 2,363 and can easily be divided by 8.
2,360 ÷ 8 = 295
2,363 ÷ 8 is about 295
What number close to 2,363 is easy to divide by 8?
2,400 is close to 2,363. What basic fact can you use?
2,400 ÷ 8
Choose 2,400 because it is close to 2,363 and can easily be divided by 8.
24 ÷ 8 = 3
2,400 ÷ 8= 300
2,363 ÷ 8 is about 300
Question 14.
1,649 ÷ 5
_____ ÷ 5 = _____
_____ ÷ 5 = _____
Answer: The quotient is between 329 and 330
Explanation:
What number close to 1,649 is easy to divide by 5?
1,645 is close to 1,649. What basic fact can you use?
1,645 ÷ 5
Choose 1,645 because it is close to 1,649 and can easily be divided by 5.
1,645 ÷ 5 = 329
1,649 ÷ 5 is about 329
What number close to 1,650 is easy to divide by 5?
1,650 is close to 1,649. What basic fact can you use?
1,650 ÷ 5
Choose 1,650 because it is close to 1,649 and can easily be divided by 5.
1,650 ÷ 5 = 330
1,649 ÷ 5 is about 330
Question 15.
5,535 ÷ 7
_____ ÷ 7 = _____
_____ ÷ 7 = _____
Answer: The quotient is between 790 and 791
Explanation:
What number close to 5,535 is easy to divide by 7?
5,530 is close to 5,535. What basic fact can you use?
5,530 ÷ 7
Choose 5,530 because it is close to 5,535 and can easily be divided by 7.
553 ÷ 7 = 79
5,530 ÷ 7 = 790
5,535 ÷ 7 is about 790
What number close to 5,535 is easy to divide by 7?
5,537 is close to 5,535. What basic fact can you use?
5,537 ÷ 7
Choose 5,537 because it is close to 5,535 and can easily be divided by 7.
553 ÷ 7 = 79
5,537 ÷ 7 = 791
5,535 ÷ 7 is about 791
Question 16.
3,640 ÷ 6
_____ ÷ 6 = _____
_____ ÷ 6 = _____
Answer: The quotient is between 606 and 607
Explanation:
What number close to 3,640 is easy to divide by 6?
3,636 is close to 3,640. What basic fact can you use?
3,636 ÷ 6
Choose 3,636 because it is close to 3,640 and can easily be divided by 6.
36 ÷ 6 = 6
3,636 ÷ 6 = 606
3,640 ÷ 6 is about 606
What number close to 3,640 is easy to divide by 6?
3,642 is close to 3,640. What basic fact can you use?
3,642 ÷ 6
Choose 3,642 because it is close to 3,640 and can easily be divided by 6.
3,642 ÷ 6 = 607
3,640 ÷ 6 is about 607
Problem Solving
Question 17.
A CD store sold 3,467 CDs in 7 days. About the same number of CDs were sold each day. About how many CDs did the store sell each day?
about _____ CDs
Answer: 495(approx)
Explanation:
Total number of CDs in the store= 3,467
Number of days= 7
Number of CDs sold on one day= 3,467 ÷ 7=495(approx)
Question 18.
Marcus has 731 books. He puts about the same number of books on each of 9 shelves in his a bookcase. About how many books are on each shelf?
about _____ books
Answer: 81 books(approx)
Explanation:
Total number of books Marcus has= 731
Number of shelves= 9
Number of books on each shelf= 731÷9= 81 (approx)
Common Core – Page No. 226
Lesson Check
Question 1.
Jamal is planting seeds for a garden nursery. He plants 9 seeds in each container. If Jamal has 296 seeds to plant, about how many containers will he use?
Options:
a. about 20
b. about 30
c. about 200
d. about 300
Answer: b. about 30
Explanation:
Total number of seeds Jamal has= 296
Number of seeds placed in each container= 9
Number of containers Jamal used= 296÷9= 32.8=33 (approx)
Therefore, the number of containers used is about 30
Question 2.
Winona purchased a set of vintage beads. There are 2,140 beads in the set. If she uses the beads to make bracelets that have 7 beads each, about how many bracelets can she make?
Options:
a. about 30
b. about 140
c. about 300
d. about 14,000
Answer: c. about 300
Explanation:
Total number of beads Winona has= 2,140
Number of beads in each bracelet= 7
Number of bracelets made= 2,140÷7=305.7=306(approx)
Therefore, the number of bracelets made are about 30
Spiral Review
Question 3.
A train traveled 360 miles in 6 hours. How many miles per hour did the train travel?
Options:
a. 60 miles per hour
b. 66 miles per hour
c. 70 miles per hour
d. 600 miles per hour
Answer: a. 60 miles per hour
Explanation:
Total number of miles travelled by the train= 360
Time taken by the train to cover 360 miles= 6 hours
Number of miles travelled in each hour= 360÷6=60 miles
Question 4.
An orchard has 12 rows of pear trees. Each row has 15 pear trees. How many pear trees are there in the orchard?
Options:
a. 170
b. 180
c. 185
d. 190
Answer: b. 180
Explanation:
Number of rows of pear trees in an orchard= 12
Number of pear trees in each row=15
Total number of pear trees in the orchard= 12 x 15=180
Question 5.
Megan rounded 366,458 to 370,000. To which place did Megan round the number?
Options:
a. hundred thousand
b. ten thousand
c. thousands
d. hundreds
Answer: b. ten thousand
Explanation:
The given number is 366,458, the ten thousand place digit has 6 which while rounding off should be changed to the next consecutive number and the digits in the other places should be written as zeroes.
Question 6.
Mr. Jessup, an airline pilot, flies 1,350 miles a day. How many miles will he fly in 8 days?
Options:
a. 1,358 miles
b. 8,400 miles
c. 10,800 miles
d. 13,508 miles
Answer: c. 10,800 miles
Explanation:
Number of miles flew by Mr.Jessup in one day= 1,350 miles
Number of days=8
Total number of miles flew by Mr.Jessup in 8 days= 1,350 x 8= 10,800 miles
Page No. 229
Model the division on the grid.
Question 1.
26 ÷ 2 = (□ ÷ 2) + (□ ÷ 2)
= □ + □
= □

Type below:
_________
Answer: 26 ÷ 2 = (20 ÷ 2) + (6 ÷ 2)
= 10 + 3
= 13
Explanation:
A. Outline a rectangle on a grid to model 26 ÷ 2. Shade columns of 2 until you have 26 squares.
How many groups of 2 can you make?
B. Think of 26 as 20 + 6. Break apart the model into two rectangles to show (20 + 6 ) ÷ 2. Label and shade the smaller rectangles. Use two different colours.
C. Each rectangle models a division.
26 ÷ 2 = (20÷ 2 ) + (6÷ 2)
= 10+ 3
= 13
Question 2.
45 ÷ 3 = (□ ÷ 3) + (□ ÷ 3)
= □ + □
= □

Type below:
_________
Answer: 45 ÷ 3 = (15 ÷ 3) + (30 ÷ 3)
= 5 + 10
= 15
Explanation:
A. Outline a rectangle on a grid to model 45 ÷ 3.
Shade columns of 3 until you have 45 squares.
How many groups of 3 can you make? _
B. Think of 45 as 15 + 30. Break apart the model into two rectangles to show (15 + 30 ) ÷ 3. Label and shade the smaller rectangles. Use two different colours.
C. Each rectangle models a division.
45 ÷ 3 = (15÷ 3 ) + (30÷ 3 )
= 5 + 10
= 15
Find the quotient.
Question 3.
82 ÷ 2 = (□ ÷ 2) + (□ ÷ 2)
= □ + □
= □
______
Answer: 82 ÷ 2 = (80 ÷ 2) + ( 2÷ 2)
= 40 + 1
= 41
Explanation:
A. Outline a rectangle on a grid to model 82 ÷ 2. Shade columns of 2 until you have 80 squares.
How many groups of 2 can you make?
B. Think of 82 as 80 + 2. Break apart the model into two rectangles to show (80 + 2 ) ÷ 2. Label and shade the smaller rectangles. Use two different colors.
C. Each rectangle models a division.
82 ÷ 2 = (80 ÷ 2 ) + (2÷ 2)
= 40 + 1
= 41
Question 4.
208 ÷ 4 = (□ ÷ 4) + (□ ÷ 4)
= □ + □
= □
______
Answer: 208 ÷ 4 = (200 ÷ 4) + (8 ÷ 4)
= 50 + 4
= 54
Explanation:
A. Outline another model to show 208 ÷ 4.
How many groups of 4 can you make?
B. Think of 208 as 200 + 8. Break apart the model, label, and shade to show two divisions.
208 ÷ 4 = (200 ÷ 4 ) + (8 ÷ 4 )
= 50 + 4
= 54
Use base-ten blocks to model the quotient.
Then record the quotient.
Question 5.
88 ÷ 4 = ______
Answer: 22
Explanation:
A. Outline another model to show 88 ÷ 4.
How many groups of 4 can you make?
B. Think of 88 as 80 + 8. Break apart the model, label, and shade to show two divisions.
88 ÷ 4 = (80 ÷ 4 ) + (8 ÷ 4 )
= 40 + 4
= 44
Question 6.
36 ÷ 3 = ______
Answer: 12
Explanation:
A. Outline a rectangle on a grid to model 36 ÷ 3.
Shade columns of 3 until you have 36 squares.
How many groups of 3 can you make? _
B. Think of 36 as 6 + 30. Break apart the model into two rectangles to show (6 + 30 ) ÷ 3. Label and shade the smaller rectangles. Use two different colours.
C. Each rectangle models a division.
36 ÷ 3 = (30÷ 3 ) + (6÷ 3 )
= 10 + 2
= 12
Question 7.
186 ÷ 6 = ______
Answer: 31
Explanation:
A. Outline a rectangle on a grid to model 186 ÷ 6.
Shade columns of 18 until you have 180 squares.
How many groups of 6 can you make? _
B. Think of 186 as 6 + 180. Break apart the model into two rectangles to show (6 + 180 ) ÷ 6. Label and shade the smaller rectangles. Use two different colours.
C. Each rectangle models a division.
186 ÷ 6 = (180÷ 6 ) + (6÷ 6 )
= 30 + 1
= 31
Question 8.
Explain how you can model finding quotients using the Distributive Property.
Type below:
_________
Answer: We can use the Distributive Property to break apart numbers to
make them easier to divide.
Explanation:
50
The Distributive Property of division says that dividing a sum by
a number is the same as dividing each addend by the number
and then adding the quotients.
Question 9.
Justin earned $50 mowing lawns and $34 washing cars. He wants to divide his money into 3 equal accounts. How much will he put in each account? Explain.
$ ______
Answer: $28
Explanation:
The amount earned by Justin on mowing lawns=$50
The amount earned by Justin on washing cars=$34
Total amount earned=$50 + $34= $84
Number of parts into which he wanted to divide the amount he earned= 3
The amount put in each account= $84 ÷ 3 = $28
Page No. 230
Question 10.
Christelle went to a gift shop. The shop sells candles in a variety of sizes and colors. The picture shows a display of candles. Write a problem that can be solved using the picture.

Pose a problem. Solve your problem
Answer:
Question: How many candles are there in the gift shop?
Explanation:
Count the number of candles in the rows and columns and then multiply them, by this we can find out the total number of candles in the gift shop.
Describe how you could change the problem by changing the number of rows of candles. Then solve the problem.
Type below:
_________
Answer: There will be no change in the solution by changing the number of rows of candles.
Explanation:
By changing the number of rows of candles the number of columns increase but there will be no change in the total number of candles.
Question 11.
For 11a–11d, choose Yes or No to indicate if the expression shows a way to break apart the dividend to find the quotient 147 ÷ 7.
a. (135 ÷ 7) + (10 ÷ 7)
i. yes
ii. no
Answer: ii. no
Explanation:
Because 137+10 is not equal to 147
Question 11.
b. (147 ÷ 3) + (147 ÷ 4)
i. yes
ii. no
Answer: ii. no
Explanation:
Because according to the distributive property we need to divide the dividend into two parts, but not the divisor.
Question 11.
c. (140 ÷ 7) + (7 ÷ 7)
i. yes
ii. no
Answer: i. yes
Explanation:
147 ÷ 7
STEP1 Find the nearest estimates of the number 147
STEP2 We can break the number 147 into 140 + 7
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (140 ÷ 7) + (7 ÷ 7)
STEP5 Add quotients of the above 20 +1= 21
Question 11.
d. (70 ÷ 7) + (77 ÷ 7)
i. yes
ii. no
Answer: i. yes
Explanation:
147 ÷ 7
STEP1 Find the nearest estimates of the number 147
STEP2 We can break the number 147 into 70 + 77
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (70 ÷ 7) + (77 ÷ 7)
STEP5 Add quotients of the above 10 +11= 21
Common Core – Page No. 231
Division and the Distributive Property
Find the quotient.
Question 1.
54 ÷ 3 = (30 ÷ 3) + (24 ÷ 3)
= 10 + 8
= 18
Answer: 18
Explanation:
54 ÷ 3
STEP1 Find the nearest estimates of the number 54
STEP2 We can break the number 54 into 30 + 24
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (30 ÷ 3) + (24÷ 3)
STEP5 Add quotients of the above 10 +8= 18
Question 2.
81 ÷ 3 = ______
Answer: 27
Explanation:
81 ÷ 3
STEP1 Find the nearest estimates of the number 81
STEP2 We can break the number 81 into 21 + 60
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (60 ÷ 3) + (21 ÷ 3)
STEP5 Add quotients of the above 20 +7= 27
Question 3.
232 ÷ 4 = ______
Answer: 58
Explanation:
232 ÷ 4
STEP1 Find the nearest estimates of the number 232
STEP2 We can break the number 232 into 200 + 32
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (200 ÷ 4) + (32 ÷ 4)
STEP5 Add quotients of the above 50 +8= 58
Question 4.
305 ÷ 5 = ______
Answer: 61
Explanation:
305 ÷ 5
STEP1 Find the nearest estimates of the number 305
STEP2 We can break the number 305 into 300 + 5
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (300 ÷ 5) + (5 ÷ 5)
STEP5 Add quotients of the above 60 +1= 61
Question 5.
246 ÷ 6 = ______
Answer: 41
Explanation:
246 ÷ 6
STEP1 Find the nearest estimates of the number 246
STEP2 We can break the number 246 into 240 + 6
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (240 ÷ 6) + (6 ÷ 6)
STEP5 Add quotients of the above 40 +1= 41
Question 6.
69 ÷ 3 = ______
Answer: 23
Explanation:
69 ÷ 3
STEP1 Find the nearest estimates of the number 69
STEP2 We can break the number 69 into 60 + 9
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (60 ÷ 3) + (9 ÷ 3)
STEP5 Add quotients of the above 20 +3= 23
Question 7.
477 ÷ 9 = ______
Answer: 53
Explanation:
477 ÷ 9
STEP1 Find the nearest estimates of the number 477
STEP2 We can break the number 477 into 450 + 27
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (450 ÷ 9) + (27 ÷ 9)
STEP5 Add quotients of the above 50 +3= 53
Question 8.
224 ÷ 7 = ______
Answer: 32
Explanation:
224 ÷ 7
STEP1 Find the nearest estimates of the number 224
STEP2 We can break the number 224 into 210 + 14
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (210 ÷ 7) + (14 ÷ 7)
STEP5 Add quotients of the above 30 +2= 32
Question 9.
72 ÷ 4 = ______
Answer: 18
Explanation:
72 ÷ 4
STEP1 Find the nearest estimates of the number 72
STEP2 We can break the number 72 into 40 + 32
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (40 ÷ 4) + (32 ÷ 4)
STEP5 Add quotients of the above 10 +8= 18
Question 10.
315 ÷ 3 = ______
Answer: 105
Explanation:
315 ÷ 3
STEP1 Find the nearest estimates of the number 315
STEP2 We can break the number 315 into 300 + 15
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (300 ÷ 3) + (15 ÷3)
STEP5 Add quotients of the above 100 +5= 105
Problem Solving
Question 11.
Cecily picked 219 apples. She divided the apples equally into 3 baskets. How many apples are in each basket?
______ apples
Answer: 73 apples
Explanation:
The total number of apples Cecily picked= 219 apples
Number of parts into which she wanted to divide the apples= 3
Number of apples in each part = Quotient of 147 ÷ 7
STEP1 Find the nearest estimates of the number 219
STEP2 We can break the number 219 into 210 + 9
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (210 ÷ 3) + (9 ÷ 3)
STEP5 Add quotients of the above 70 +3= 73
Question 12.
Jordan has 260 basketball cards. He divides them into 4 equal groups. How many cards are in each group?
______ cards
Answer: 65 cards
Explanation:
The total number of basketball cards Jordan has= 260 basketball cards
Number of parts into which he wanted to divide the cards= 4
Number of apples in each part = Quotient of 260 ÷ 4
STEP1 Find the nearest estimates of the number 260
STEP2 We can break the number 260 into 240 + 20
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (240 ÷ 4) + (20 ÷ 4)
STEP5 Add quotients of the above 60 +5= 65
Question 13.
The Wilsons drove 324 miles in 6 hours. If they drove the same number of miles each hour, how many miles did they drive in 1 hour?
______ miles
Answer: 54 miles
Explanation:
The total number of miles drove by Wilson= 324 miles
Number of hours he drove = 6
Number of miles drove in each hour = Quotient of 324 ÷ 6
STEP1 Find the nearest estimates of the number 324
STEP2 We can break the number 324 into 300 + 24
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (300 ÷ 6) + (24 ÷ 6)
STEP5 Add quotients of the above 50 +4= 54
Question 14.
Phil has 189 stamps to put into his stamp album. He puts the same number of stamps on each of 9 pages. How many stamps does Phil put on each page?
______ stamps
Answer: 21 stamps
Explanation:
The total number of stamps Phil has= 189 stamps
Number of pages= 9
Number of stamps put on each page = Quotient of 189 ÷ 9
STEP1 Find the nearest estimates of the number 189
STEP2 We can break the number 189 into 180 + 9
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (180 ÷ 9) + (9 ÷ 9)
STEP5 Add quotients of the above 20 +1= 21
Common Core – Page No. 232
Lesson Check
Question 1.
A landscaping company planted 176 trees in 8 equal rows in the new park. How many trees did the company plant in each row?
Options:
a. 18
b. 20
c. 22
d. 24
Answer: c. 22
Explanation:
The total number of trees in the landscaping= 176 trees
Number of rows= 8
Number of trees in each row = Quotient of 176 ÷ 8
STEP1 Find the nearest estimates of the number 176
STEP2 We can break the number 176 into 160 + 16
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (160 ÷ 8) + (16 ÷ 8)
STEP5 Add quotients of the above 20 +2= 22
Question 2.
Arnold can do 65 pushups in 5 minutes. How many pushups can he do in 1 minute?
Options:
a. 11
b. 13
c. 15
d. 17
Answer: b. 13
Explanation:
The total number of pushups done by Arnold = 65
Number of minutes spent on pushups= 5
Number of pushups done in each minute = Quotient of 65 ÷ 5
STEP1 Find the nearest estimates of the number 65
STEP2 We can break the number 65 into 60 + 5
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (60 ÷ 5) + (5 ÷ 5)
STEP5 Add quotients of the above 12 +1= 13
Spiral Review
Question 3.
Last Saturday, there were 1,486 people at the Cineplex. There were about the same number of people in each of the 6 theaters. Which is the best estimate of the number of people in each theater?
Options:
a. between 20 and 30
b. between 80 and 90
c. between 100 and 200
d. between 200 and 300
Answer: d. between 200 and 300
Explanation:
Total number of people at the Cineplex= 1,486 people
Number of theatres = 6
Number of people at each theatre= estimate of the number of people 1,486 ÷ 6
What number close to 1,486 is easy to divide by 6?
1,488 is close to 1,486. What basic fact can you use?
1,488 ÷ 6
Choose 1,488 because it is close to 1,486 and can easily be divided by 6.
1,488 ÷ 6 = 248
1,486 ÷ 6 is about 248
What number close to 1,486 is easy to divide by 6?
1,482 is close to 1,486 . What basic fact can you use?
1,482 ÷ 6
Choose 1,482 because it is close to 1,486 and can easily be divided by 6.
1,482 ÷ 6 = 247
1,486 ÷ 6 is about 247
Question 4.
Nancy walked 50 minutes each day for 4 days last week. Gillian walked 35 minutes each day for 6 days last week. Which statement is true?
Options:
a. Gillian walked 10 minutes more than Nancy.
b. Gillian walked 20 minutes more than Nancy.
c. Nancy walked 10 minutes more than Gillian.
d. Nancy walked 15 minutes more than Gillian.
Answer: d. Nancy walked 15 minutes more than Gillian.
Explanation:
Time walked by Nancy= 50 minutes
Time walked by Gillian= 35 minutes
Nancy walked more time compared to Gillian
50-35=15 minutes
Therefore, Nancy walked 15 minutes more than Gillian.
Question 5.
Three boys share 28 toy cars equally. Which best describes how the cars are shared?
Options:
a. Each gets 3 cars with 1 left over.
b. Each gets 8 cars with 2 left over.
c. Each gets 9 cars with 1 left over.
d. Each gets 10 cars with 2 left over.
Answer: c. Each gets 9 cars with 1 left over.
Explanation:
Total number of toys three boys have= 28
Number of toys each boy got= 28 ÷3=9.33
Therefore we can say that each gets 9 cars with 1 leftover.
Question 6.
An airplane flies at a speed of 474 miles per hour. How many miles does the plane fly in 5 hours?
Options:
a. 2,070 miles
b. 2,140 miles
c. 2,370 miles
d. 2,730 miles
Answer: c. 2,370 miles
Explanation:
Number of miles flew by aeroplane in one hour= 474
Number of hours the aeroplane flew= 5 hours
Total number of miles flew in 5 hours= 474 x 5= 2,370 miles
Page No. 233
Choose the best term from the box to complete the sentence.

Question 1.
A number that is the product of a number and a counting number is called a _____________.
___________
Answer: Multiple
Explanation:
3 x 4 = 12
In which 4 is a multiple and also 4 is a counting number
Question 2.
Numbers that are easy to compute mentally are called _____________.
___________
Answer: Compatible numbers
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers.
Question 3.
When a number cannot be divided evenly, the amount left over is called the _____________.
___________
Answer: Remainder
Explanation:
When we divide 10 with 3 there will be 1 remaining, which is called remainder.
Divide. Draw a quick picture to help.
Question 4.
26 ÷ 3
_____ R _____
Answer: Quotient: 8 Remainder: 2
Explanation:




Quotient:
A. Use 26 counters to represent the 26 dominoes. Then draw 3 circles to represent the divisor.
B. Share the counters equally among the 8 groups by placing them in the circles.
C. Number of circles filled= quotient of 26 ÷ 3 = 8
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 2
Question 5.
19 ÷ 4
_____ R _____
Answer: Quotient: 4 Remainder: 3
Explanation:







Quotient:
A. Use 19 counters to represent the 19 dominoes. Then draw 4 circles to represent the divisor.
B. Share the counters equally among the 4 groups by placing them in the circles.
C. Number of circles filled= quotient of 19 ÷ 4 = 4
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 3
Use basic facts and place value to find the quotient.
Question 6.
810 ÷ 9 = _____
Answer: 90
Explanation:
STEP 1 Identify the basic fact. 81 ÷ 9
STEP 2 Use place value. 810 = 81 tens
STEP 3 Divide. 81 tens ÷ 9 = 9 tens
810 ÷ 9 = 90
Question 7.
210 ÷ 7 = _____
Answer: 30
Explanation:
STEP 1 Identify the basic fact. 21 ÷ 7
STEP 2 Use place value. 210 = 21 tens
STEP 3 Divide. 21 tens ÷ 7 = 3 tens
210 ÷ 7 = 30
Question 8.
3,000 ÷ 6 = _____
Answer: 500
Explanation:
STEP 1 Identify the basic fact. 30 ÷ 6
STEP 2 Use place value. 3,000 = 30 hundreds
STEP 3 Divide. 30 hundreds ÷ 6 = 5 hundreds
3,000 ÷ 6 = 500
Use compatible numbers to estimate the quotient.
Question 9.
635 ÷ 9
about _____
Answer: 70
Explanation:
What number close to 635 is easy to divide by 9?
630 is close to 635. What basic fact can you use?
630 ÷ 9
Choose 630 because it is close to 635 and can easily be divided by 9.
63 ÷ 9 = 7
630 ÷ 9 = 70
635 ÷ 9 is about 70
Question 10.
412 ÷ 5
about _____
Answer: 82
Explanation:
What number close to 412 is easy to divide by 5?
410 is close to 412. What basic fact can you use?
410 ÷ 5
Choose 410 because it is close to 412 and can easily be divided by 5.
410 ÷ 5 = 82
412 ÷ 5 is about 82
Question 11.
490 ÷ 8
about _____
Answer: 60
Explanation:
What number close to 490 is easy to divide by 8?
480 is close to 490. What basic fact can you use?
480 ÷ 8
Choose 480 because it is close to 490 and can easily be divided by 8.
48 ÷ 8 = 6
480 ÷ 8 = 60
490 ÷ 8 is about 60
Use grid paper or base-ten blocks to model the quotient.
Then record the quotient.
Question 12.
63 ÷ 3 = _____
Answer: 21
Explanation:
A. Outline another model to show 63 ÷ 3.
How many groups of 3 can you make?
B. Think of 63 as 60 + 3. Break apart the model, label, and shade to show two divisions.
63 ÷ 3 = (60 ÷ 3 ) + (3 ÷ 3 )
= 20 + 1
= 21
Question 13.
85 ÷ 5 = _____
Answer: 17
Explanation:
A. Outline another model to show 85 ÷ 5.
How many groups of 5 can you make?
B. Think of 85 as 80 + 5. Break apart the model, label, and shade to show two divisions.
85 ÷ 5 = (80 ÷ 5 ) + (5 ÷ 5)
= 16 + 1
= 17
Question 14.
168 ÷ 8 = _____
Answer:21
Explanation:

A. Outline another model to show 168 ÷ 8.
How many groups of 8 can you make?
B. Think of 168 as 160 + 8. Break apart the model, label, and shade to show two divisions.
168 ÷ 8 = (160 ÷ 8 ) + (8 ÷ 8 )
= 20 + 1
= 21
Page No. 234
Question 15.
Ana has 296 coins in her coin collection. She put the same number of coins in each of 7 jars. About how many coins are in each jar?
about _____ coins
Answer: 42
Explanation:
The total number of coins Ana has= 296 coins
Number of Jars= 7
Number of coins in each Jar= 296 ÷ 7 = 42 coins
Question 16.
Which two estimates is the quotient 345 ÷ 8 between?
_____ and _____
Answer: The quotient is between 42 and 43
Explanation:
What number close to 345 is easy to divide by 8?
336 is close to 1,624. What basic fact can you use?
336 ÷ 8
Choose 336 because it is close to 345 and can easily be divided by 8.
336 ÷ 8 = 42
345 ÷ 8 is about 42
What number close to 345 is easy to divide by 8?
344 is close to 345. What basic fact can you use?
344 ÷ 8
Choose 344 because it is close to 345 and can easily be divided by 8.
344 ÷ 8 = 43
345 ÷ 8 is about 43
Question 17.
A total of 8,644 people went to the football game. Of those people, 5,100 sat on the home side and the rest sat on the visitor’s side. If the people sitting on the visitor’s side filled 8 equal-sized sections, about how many people sat in each of the sections?
about _____ people
Answer: 443
Explanation:
Total number of people in the football game= 8,644
Number of people who sat on the homeside= 5,100
Number of people who sat on the visitor’s side= 3,544
Number of equal-sized sections= 8
Number of people who sat in each of the sections= 3,544 ÷ 8= 443
Question 18.
There are 4 students on a team for a relay race. How many teams can be made from 27 students?
_____ teams
Answer: 7
Explanation:
The total number of students= 27
Number of students in each team= 4
Number of teams = 27 ÷ 4= 6.75 = 7 (approx)
Question 19.
Eight teams of high school students helped clean up trash in the community. Afterwards, they shared 23 pizzas equally. How many pizzas did each team get?
_____ \(\frac{ □ }{ □ }\)
Answer: 3
Explanation:
Total number of pizzas= 23
Number of teams= 8
Number of pizzas each team got= 23 ÷ 8=2.8=3(approx)
Page No. 237
Use repeated subtraction to divide.
Question 1.
84 ÷ 7
_____
Answer: 12
Explanation:
A. Begin with 84 counters. Subtract 7 counters.
B. Subtract 7 counters from 84 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 12.
Question 2.
60 ÷ 4
_____
Answer: 15
Explanation:
A. Begin with 60 counters. Subtract 4 counters.
B. Subtract 4 counters from 60 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 15.
Question 3.
91 ÷ 8
_____ R _____
Answer: 11.3=11(approx)
Explanation:
A. Begin with 91 counters. Subtract 8 counters.
B. Subtract 8 counters from 91 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 11
Draw a number line to divide.
Question 4.
65 ÷ 5 = _____
Answer: 13
Explanation:
A. Begin with 65 counters. Subtract 5 counters.
B. Subtract 5 counters from 65 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 13
Question 5.
Use Appropriate Tools Can you divide 32 by 3 evenly? Use the number line to explain your answer.

Type below:
__________
Answer: 11 (approx)
Explanation:
How many equal groups of 3 did you subtract?
So, 32 ÷ 3 = 10.8=11(approx).
Question 6.
John has $40 to spend at the yard sale. He buys 6 books for $2 each. He would like to spend the rest of his money on model cars for his collection. If the cars cost $7 each, how many can he buy? Explain.
_____ cars
Answer: 4 cars
Explanation:
Total amount John spent at the yard sale= $40
Number of books= 6
Cost of each book= $2
Cost of 6 books= 6 x $2 = $12
Amount left after John bought 6 books= $40 – $12 = $28
Cost of each car= $7
Number of cars bought = $28 ÷ $7 = $4
Page No. 238
Question 7.
A new playground will be 108 feet long. Builders need to allow 9 feet of space for each piece of climbing equipment. They want to put as many climbers along the length of the playground as possible. How many climbers can they place?

a. What are you asked to find?
Type below:
__________
Answer: 12
Explanation:
A. Begin with 108 counters. Subtract 9 counters.
B. Subtract 9 counters from 108 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 12.
Question 7.
b. How can you use repeated subtraction to solve the problem?
Type below:
__________
Answer: Repeated subtraction is a method to solve and find the quotient.
Explanation:
Example:
A. Begin with 65 counters. Subtract 5 counters.
B. Subtract 5 counters from 65 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 13
Question 7.
c. Tell why you might use multiples of the divisor to solve the problem.
Type below:
__________
Answer: The multiple which divides 108 is 12
Explanation:
The number 108 has multiples which divide 108 evenly,
1 x 108 =108
2 x 54 =108
3 x 36 =108
4 x 27 =108
6 x 18 =108
9 x 12 =108
12 x 9 =108
18 x 6 =108
27 x 4 =108
36 x 3 =108
54 x 2 =108
108 x 1 =108
Multiples which divide 108 are 1,2,3,4,5,6,9,12,18,27,36,54,108.
Question 7.
d. Show steps to solve the problem.
Type below:
__________
Answer: 108 ÷ 9 =12
Explanation:
A. Begin with 108 counters. Subtract 9 counters.
B. Subtract 9 counters from 108 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 12
Question 7.
e. Complete the sentences.
There are _______ equal parts of the playground, each _______ feet long.
So, _______ climbers can fit along the length of the playground.
Type below:
__________
Answer: There are ___108____ equal parts of the playground, each __09_____ feet long. So, __12_____ climbers can fit along the length of the playground.
Explanation:
A new playground will be 108 feet long.
Builders need to allow 9 feet of space for each piece of climbing equipment.
Number of climbers that can fit along the length of the playground= 108 ÷ 9 =12
Question 8.
Which model matches each expression?
Write the letter on the line next to the model.
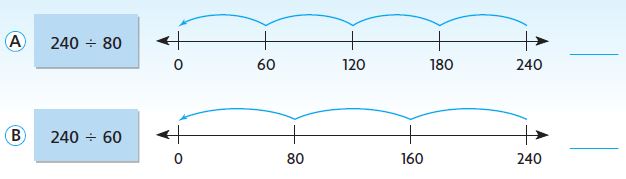
Type below:
__________
Answer: 240 ÷ 80 expression resembles the second model while 240 ÷ 60 expression resembles the first model.
Explanation:
240 ÷ 80
A. Draw a number line with 80 as each interval.
B. Draw up to 240 and count the intervals, it gives the quotient.
C. The quotient is 3
240 ÷ 60
A. Draw a number line with 60 as each interval.
B. Draw up to 240 and count the intervals, it gives the quotient.
C. The quotient is 4
Common Core – Page No. 239
Divide Using Repeated Subtraction
Use repeated subtraction to divide.
Question 1.
42 ÷ 3 = 14
3)\(\overline { 42 } \)
-30 ← 10 × 3 | 10
——-
12
-12 ← 4 × 3 | +4
——- ———–
0 14
Answer: 14
Explanation:
A. Begin with 42 counters. Subtract 3 counters.
B. Subtract 3 counters from 42 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 14
Question 2.
72 ÷ 4 = _____
Answer: 18
Explanation:
A. Begin with 72 counters. Subtract 4 counters.
B. Subtract 4 counters from 72 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 18
Question 3.
93 ÷ 3 = _____
Answer: 31
Explanation:
A. Begin with 93 counters. Subtract 3 counters.
B. Subtract 3 counters from 93 and repeat the processes until the remainder cannot be subtracted from the divisor.
C. Record the number of counters left and the number of times you subtracted.
D. The number of times you subtracted is the quotient is 31
Question 4.
35 ÷ 4 = _____ r _____
Answer: 8r3
Explanation:
Quotient:
A. Use 35 counters to represent the 35 dominoes. Then draw 4 circles to represent the divisor.
B. Share the counters equally among the 4 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 35 ÷ 4
D. Number of circles are equally filled with 4 counters, therefore, the quotient is 8
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 3
For 35 ÷ 4, the quotient is 8 and the remainder is 3, or 8 r3.
Question 5.
93 ÷ 10 = _____ r _____
Answer: 9r3
Explanation:
Quotient:
A. Use 93 counters to represent the 93 dominoes. Then draw 10 circles to represent the divisor.
B. Share the counters equally among the 10 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 93 ÷ 10
D. Number of circles are equally filled with 10 counters, therefore, the quotient is 9
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 3
For 93 ÷ 10, the quotient is 9 and the remainder is 3, or 9 r3.
Question 6.
86 ÷ 9 = _____ r _____
Answer: 9r5
Explanation:
Quotient:
A. Use 86 counters to represent the 86 dominoes. Then draw 9 circles to represent the divisor.
B. Share the counters equally among the 9 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 86 ÷ 9
D. Number of circles are equally filled with 9 counters, therefore, the quotient is 9
Remainder:
The number of counters left over is the remainder. The number of counters leftover= 5
For 86 ÷ 9, the quotient is 9 and the remainder is 5, or 9 r5.
Draw a number line to divide.
Question 7.
70 ÷ 5 = _____
Answer: 14
Explanation:
A. Draw a number line with 5 as each interval.
B. Draw up to 70 and count the intervals, it gives the quotient.
C. The quotient is 14
Problem Solving
Question 8.
Gretchen has 48 small shells. She uses 2 shells to make one pair of earrings. How many pairs of earrings can she make?
_____ pairs
Answer: 24 pairs
Explanation:
Total number of small shells= 48
Number of shells used to make one pair of earrings = 2
Number of pair of earrings made = 48 ÷ 2 =24
Question 9.
James wants to purchase a telescope for $54. If he saves $3 per week, in how many weeks will he have saved enough to purchase the telescope?
_____ weeks
Answer: $18
Explanation:
Cost of the telescope=$54
Amount saved each week = $3
Number of weeks he has to save the money to purchase the telescope = $54 ÷ $3 = $18
Common Core – Page No. 240
Lesson Check
Question 1.
Randall collects postcards that his friends send him when they travel. He can put 6 cards on one scrapbook page. How many pages does Randall need to fit 42 postcards?
Options:
a. 3
b. 4
c. 6
d. 7
Answer: d. 7
Explanation:
Total number of postcards Randall has = 42 postcards
Number of postcards on one scrapbook page = 6 cards
Number of pages needed to fit the postcards = 42 ÷ 6=7
Question 2.
Ari stocks shelves at a grocery store. He puts 35 cans of juice on each shelf. The shelf has 4 equal rows and another row with only 3 cans. How many cans are in each of the equal rows?
Options:
a. 6
b. 7
c. 8
d. 9
Answer: c. 8
Explanation:
Total number of cans of juice on each shelf = 35
Number of rows = 4
Number of cans on the other shelf = 3
Number of cans placed on the first shelf = 35 – 3 = 32
Number of juice cans in the first row = 32 ÷ 4 = 8 cans
Spiral Review
Question 3.
Fiona sorted her CDs into separate bins. She placed 4 CDs in each bin. If she has 160 CDs, how many bins did she fill?
Options:
a. 4
b. 16
c. 40
d. 156
Answer: c. 40
Explanation:
Total number of CD’s in Fiona has = 160 CD’s
Number of CD’s placed in each bin = 4
Number of bins required to place the CD’s = 160 ÷ 4 = 40
Question 4.
Eamon is arranging 39 books on 3 shelves. If he puts the same number of books on each shelf, how many books will there be on each shelf?
Options:
a. 11
b. 12
c. 13
d. 14
Answer: c. 13
Explanation:
Total number of books Eamon has = 39 books
Number of shelves = 3
Number of books in each shelf = 39 ÷ 3 = 13
Question 5.
A newborn boa constrictor measures 18 inches long. An adult boa constrictor measures 9 times the length of the newborn plus 2 inches. How long is the adult?
Options:
a. 142 inches
b. 162 inches
c. 164 inches
d. 172 inches
Answer: c. 164 inches
Explanation:
Length of newborn boa constrictor = 18 inches
Length of an adult boa constrictor = 9 x Length of newborn boa constrictor = 9 x 18 = 162
Total length of an adult boa constrictor = 162 + 2 = 164 inches
Question 6.
Madison has 6 rolls of coins. Each roll has 20 coins. How many coins does Madison have in all?
Options:
a. 110
b. 120
c. 125
d. 130
Answer: b. 120
Explanation:
Number of rolls of coins = 6
Number of coins in each roll = 20
Total number of coins Madison has = 20 x 6 = 120
Page No. 243
Question 1.
Lacrosse is played on a field 330 ft long. How many yards long is a lacrosse field? (3 feet = 1 yard)
Divide. Use partial quotients.

So, the lacrosse field is _____ yards long.
______ yards
Answer: 37 yards (approx)
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor. For example, you know that you can make at least 100 ft which is long 33 yards.
Continue subtracting until the remaining number is less than the multiple, 3.
STEP 2
Subtract smaller multiples, such as 3 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 110 ft = 110 ÷ 3 = 36.6 yards = 37 yards (approx).
Divide. Use partial quotients.
Question 2.
3)\(\overline { 225 } \)
____
Answer: 75
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 50 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 3.
STEP 2
Subtract smaller multiples, such as 3 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 50 x 3 = 150 : 225 – 150 = 75
3 x 25 = 75 : 75 – 75 = 0
Therefore the quotient is 75 ( 50 + 25)
Divide. Use rectangular models to record the partial quotients.
Question 3.
428 ÷ 4 =
____
Answer: 107
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 50 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 4.
STEP 2
Subtract smaller multiples, such as 4 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 50 x 4 = 200 : 428 – 200 = 228
4 x 50 = 200 : 228 – 200 = 28
7 x 4 = 28 : 28 – 28 = 0
Therefore the quotient is 107 ( 50 + 50 + 7)
The rectangle models are given below :
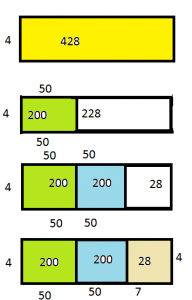
Divide. Use partial quotients.
Question 4.
7)\(\overline { 224 } \)
____
Answer: 32
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 30 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 7.
STEP 2
Subtract smaller multiples, such as 7 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 30 x 7 = 210 : 224 – 210 = 14
7 x 2 = 14 : 14 – 14 = 0
Therefore the quotient is 32 ( 30 + 2)
Question 5.
7)\(\overline { 259 } \)
____
Answer: 37
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 30 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 7.
STEP 2
Subtract smaller multiples, such as 7 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 30 x 7 = 210 : 225 – 210 = 49
7 x 7 = 49 : 49 – 49 = 0
Therefore the quotient is 37 ( 30 + 7)
Question 6.
8)\(\overline { 864 } \)
____
Answer: 108
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 8.
STEP 2
Subtract smaller multiples, such as 8 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 8 = 800 : 864 – 800 = 64
8 x 8 = 64 : 64 – 64 = 0
Therefore the quotient is 108 ( 100 + 8)
Question 7.
6)\(\overline { 738 } \)
____
Answer: 123
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 6.
STEP 2
Subtract smaller multiples, such as 6 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 6 = 600 : 738 – 600 = 138
6 x 23 = 138 : 138 – 138 = 0
Therefore the quotient is 123 ( 100 + 23)
Divide. Use rectangular models to record the partial quotients.
Question 8.
328 ÷ 2 =
____
Answer: 164
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 2.
STEP 2
Subtract smaller multiples, such as 2 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 2 = 200 : 328 – 200 = 128
2 x 64 = 128 : 128 – 128 = 0
Therefore the quotient is 164 ( 100 + 64)
The rectangle models are given below :
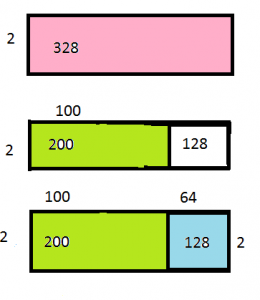
Question 9.
475 ÷ 5 =
____
Answer: 95
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 90 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 5.
STEP 2
Subtract smaller multiples, such as 5 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 90 x 5 = 450 : 475 – 450 = 25
5 x 5 = 25 : 25 – 25 = 0
Therefore the quotient is 95 (90 + 5)
The rectangle models are given below :
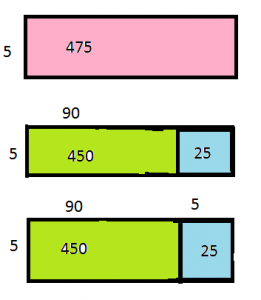
Question 10.
219 ÷ 3 =
____
Answer: 73
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 70 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 3.
STEP 2
Subtract smaller multiples, such as 3 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 70 x 3 = 210 : 219 – 210 = 9
3 x 3 = 9 : 9 – 9 = 0
Therefore the quotient is 73 ( 70 + 3)
The rectangle models are given below :
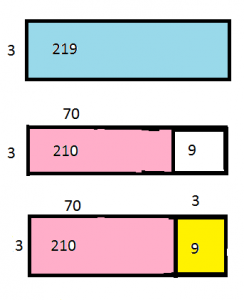
Question 11.
488 ÷ 4 =
____
Answer: 122
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 4.
STEP 2
Subtract smaller multiples, such as 4 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 4 = 400 : 488 – 400 = 88
4 x 22 = 88 : 88 – 88 = 0
Therefore the quotient is 122 ( 100 + 22)
The rectangle models are given below :
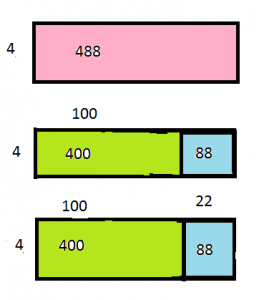
Question 12.
Use Reasoning What is the least number you can divide by 5 to get a three-digit quotient? Explain how you found your answer.
____
Answer: The quotient can be a three-digit number or a two-digit number.
Explanation:
Example:
475 ÷ 5 =
____
Answer: 95
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 90 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 5.
STEP 2
Subtract smaller multiples, such as 5 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 90 x 5 = 450 : 475 – 450 = 25
5 x 5 = 25 : 25 – 25 = 0
Therefore the quotient is 95 (90 + 5)
Page No. 244
Use the table for 13–15.

Question 13.
Rob wants to put 8 baseball cards on each page in an album. How many pages will he fill?
____ pages
Answer: 31 pages
Explanation:
Total number of baseball cards = 248
Number of cards in each page = 8
Number of pages required = 248 ÷ 8 = 31 pages
Question 14.
Rob filled 5 plastic boxes with hockey cards. There were the same number of cards in each box. How many cards did he put in each box? How many cards were left over?
Type below:
___________
Answer: There where 12 hockey cards in each box, number of cards leftover = 4
Explanation:
Total number of hockey cards = 64
Number of boxes = 5
Number of cards in each box = 64 ÷ 5 = 12.8 that is exactly 60 cards can be fit in 5 boxes and 12 in each box
Number of cards leftover = 64 – 60 = 4
Question 15.
Rob filled 3 fewer plastic boxes with football cards than basketball cards. He filled 9 boxes with basketball cards. How many boxes did he fill with football cards? How many football cards were in each box?
____ boxes ____ cards
Answer: 6 boxes and 16 cards in each box
Explanation:
Number of basketball cards= 189
Number of boxes in which the basketball cards were kept= 9 boxes
Number of football cards= 96
Number of boxes in which the football cards were kept = number of boxes in which the basketball cards were kept – 3 =
9-3=6boxes
Number of football cards in each box = 96 ÷ 6 =16 cards
Question 16.
Marshall can buy 5 T-shirts for $60. If each shirt costs the same amount, what is the cost of 4 T-shirts?
$ ____
Answer: $48
Explanation:
Number of T-shirts = 5
Cost of 5 T-shirts = $60
Cost of each T- shirt = $60 ÷ 5 = $12
Cost of 4 T-shirts = 12 x 4 = $48
Question 17.
Use partial quotients. Fill in the blanks.
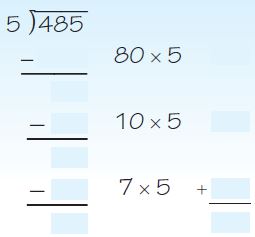
Type below:
___________
Answer: 97
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 80 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 5.
STEP 2
Subtract smaller multiples, such as 5 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 80 x 5 = 400 : 485 – 400 = 85
5 x 17 = 85 : 85 – 85 = 0
Therefore the quotient is 97 ( 80 + 17)
Common Core – Page No. 245
Divide Using Partial Quotients
Divide. Use partial quotients.
Question 1.
8)\(\overline { 184 } \)
-80 ← 10 × 8 10
——-
104
-80 ← 10 × 8 + 10
——-
-24
-24 ← 3 × 8 + 3
——– ——–
0 23
Answer: 23
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 10 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 8.
STEP 2
Subtract smaller multiples, such as 10 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 10 x 8 = 80 : 184 – 80 = 104
10 x 8 = 80 : 104 – 80 = 24 : 3 x 8 = 24 : 24 – 24 = 0
Therefore the quotient is 23 ( 10 + 10 + 3)
Question 2.
6)\(\overline { 258 } \)
_____
Answer: 43
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 40 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 6.
STEP 2
Subtract smaller multiples, such as 3 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 40 x 6 = 240 : 258 – 240 = 18
3 x 6 = 18 : 18 – 18 = 0
Therefore the quotient is 43 ( 40 + 3)
Question 3.
5)\(\overline { 630 } \)
_____
Answer: 126
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 5.
STEP 2
Subtract smaller multiples, such as 20 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 5 = 500 : 630 – 500 = 130
5 x 20 = 100 : 130 – 100 = 30 : 5 x 6 = 30 : 30 – 30 = 0
Therefore the quotient is 126 ( 100 + 20 + 6)
Divide. Use rectangular models to record the partial quotients.
Question 4.
246 ÷ 3 = _____
Answer: 82
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 80 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 3.
STEP 2
Subtract smaller multiples, such as 80 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 80 x 3 = 240 : 246 – 240 = 6
3 x 2 = 6 : 6 – 6 = 0
Therefore the quotient is 82 ( 80 + 2)
The rectangle models are given below :
Question 5.
126 ÷ 2 = _____
Answer: 63
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 60 times the divisor.
Continue subtracting until the remaining number is less than the multiple,2.
STEP 2
Subtract smaller multiples, such as 60 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 60 x 2 = 120 : 126 – 120 = 6
2 x 3 = 6 : 6 – 6 = 0
Therefore the quotient is 63 ( 60 +3)
The rectangle models are given below :
Question 6.
605 ÷ 5 = _____
Answer: 121
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 5.
STEP 2
Subtract smaller multiples, such as 20 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 5 = 500 : 605 – 500 = 105
5 x 20 = 100 : 105 – 100 = 5 : 5 x 1 = 5 : 5 – 5 = 0
Therefore the quotient is 121 ( 100 + 20 + 1)
The rectangle models are given below :
Divide. Use either way to record the partial quotients.
Question 7.
492 ÷ 3 = _____
Answer: 164
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 3.
STEP 2
Subtract smaller multiples, such as 50 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 3 = 300 : 492 – 300 = 192
50 x 3 = 150 : 192 – 150 = 42 : 3 x 14 = 42 : 42 – 42 = 0
Therefore the quotient is 164 ( 100 + 50 + 14)
Question 8.
224 ÷ 7 = _____
Answer: 32
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 30 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 7.
STEP 2
Subtract smaller multiples, such as 30 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 30 x 7 = 210 : 224 – 210 = 14
7 x 2 = 14 : 14 – 14 = 0
Therefore the quotient is 32 ( 30 + 2)
Question 9.
692 ÷ 4 = _____
Answer: 173
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 4.
STEP 2
Subtract smaller multiples, such as 100 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 4 = 400 : 692 – 400 = 392
4 x 50 = 200 : 392 – 200 = 192 : 4 x 48 = 192 : 192 – 192 = 0
Therefore the quotient is 198 ( 100 + 50 + 48)
Problem Solving
Question 10.
Allison took 112 photos on vacation. She wants to put them in a photo album that holds 4 photos on each page. How many pages can she fill?
_____ pages
Answer: 28
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 20 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 4.
STEP 2
Subtract smaller multiples, such as 20 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 20 x 4 = 80 : 112 – 80 = 32
4 x 8 = 32 : 32 – 32 = 0
Therefore the quotient is 28 ( 20 + 8)
Question 11.
Hector saved $726 in 6 months. He saved the same amount each month. How much did Hector save each month?
$ _____
Answer: $121
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 6.
STEP 2
Subtract smaller multiples, such as 100 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 6 = 600 : 726 – 600 = 126
6 x 20 = 120 : 126 – 120 = 6 : 6 x 1 = 6 : 6 – 6 = 0
Therefore the quotient is 121 ( 100 + 20 +1)
Common Core – Page No. 246
Lesson Check
Question 1.
Annaka used partial quotients to divide 145 ÷ 5. Which shows a possible sum of partial quotients?
Options:
a. 50 + 50 + 45
b. 100 + 40 + 5
c. 10 + 10 + 9
d. 10 + 4 + 5
Answer: c. 10 + 10 + 9
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 4.
STEP 2
Subtract smaller multiples, such as 10 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 10 x 5 = 50 : 145 – 50 = 95
5 x 10 = 50 : 95 – 50 = 45 : 5 x 9 = 45 : 45 – 45 = 0
Therefore the quotient is 29 ( 10 + 10 +9)
Question 2.
Mel used partial quotients to find the quotient 378 ÷ 3. Which might show the partial quotients that Mel found?
Options:
a. 100, 10, 10, 9
b. 100, 10, 10, 6
c. 100, 30, 30, 6
d. 300, 70, 8
Answer: b. 100, 10, 10, 6
Explanation:
STEP 1
Start by subtracting a greater multiple, such as 100 times the divisor.
Continue subtracting until the remaining number is less than the multiple, 3.
STEP 2
Subtract smaller multiples, such as 10 times the divisor until the remaining number is less than the divisor. In other words, keep going until you no longer a remainder is left in the place of the remainder. Then add the partial quotients to find the quotient.
So, there are 100 x 3 = 300 : 378 – 300 = 78
10 x 3 =30 : 78 – 30 = 48 : 3 x 16 = 48 : 48 – 48 = 0
Therefore the quotient is 126 ( 100 + 10 +10 + 6)
Spiral Review
Question 3.
What are the partial products of 42 × 5?
Options:
a. 9 and 7
b. 20 and 10
c. 200 and 7
d. 200 and 10
Answer: d. 200 and 10
Explanation:
STEP1
42 x 5
Start by multiplying the digit five with the units digit 2 = 5 x 2 =10
Multiply the digit 5 with 4 in the tens place = 4 x 5 = 20
Since 4 is in the tens place when we multiply 4 and 5 we must place it in the hundreds place by assuming units digit to be zero.
Therefore, the partial product of 42 x 5 = 200
Question 4.
Mr. Watson buys 4 gallons of paint that cost $34 per gallon. How much does Mr. Watson spend on paint?
Options:
a. $38
b. $126
c. $136
d. $1,216
Answer: c. $136
Explanation:
Cost of each gallon of paint = $34
Number of gallons = 4
The total cost of the gallons = $ 34 x 4 = $136
Question 5.
Use the area model to find the product 28 × 32.

Options:
a. 840
b. 856
c. 880
d. 896
Answer: d. 896
Explanation:
The whole rectangle is divided into four small rectangles the areas of these rectangles are:
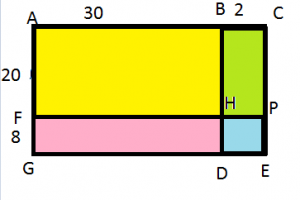
Area of yellow rectangle= 30 x 20=600
Area of green rectangle= 2 x 20 = 40
Area of pink rectangle= 8 x 30= 240
Area of blue rectangle= 2 x 8= 16
Product of 32 and 28 = Area of yellow rectangle + Area of green rectangle + Area of pink rectangle + Area of the blue rectangle = 600+40+240+16 = 896
Question 6.
An adult male lion eats about 108 pounds of meat per week. About how much meat does an adult male lion eat in one day?
Options:
a. about 14 pounds
b. about 15 pounds
c. about 16 pounds
d. about 17 pounds
Answer: b. about 15 pounds
Explanation:
Mass of meat an adult lion eats in one week = 108
Number of days in a week = 7
Mass of meat ate by the lion in one day = 108 ÷ 7 = 15.4 pounds = about 15 pounds
Page No. 249
Divide. Use base-ten blocks.
Question 1.
48 ÷ 3
_____
Answer: 16
Explanation:
A. Draw 3 circles to represent the divisor. Then use base-ten blocks to model 48. Show 48 as 4 tens and 8 ones.
B. Share the tens equally among the 3 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 3 groups.
D. There are 1 ten(s) and 6 one(s) in each group. So, the quotient is 16.
Question 2.
84 ÷ 4
_____
Answer: 21
Explanation:
A. Draw 4 circles to represent the divisor. Then use base-ten blocks to model 84. Show 84 as 8 tens and 4 ones.
B. Share the tens equally among the 4 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 4 groups.
D. There are 2 ten(s) and 1 one(s) in each group. So, the quotient is 21.
Question 3.
72 ÷ 5
_____ R _____
Answer: 14 (approx) with 2 as remainder.
Explanation:
A. Draw 5 circles to represent the divisor. Then use base-ten blocks to model 72. Show 72 as 7 tens and 2 ones.
B. Share the tens equally among the 5 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 5 groups.
D. There are 1 ten(s) and 4 one(s) in each group. So, the quotient is 14.
Question 4.
Divide. Draw a quick picture. Record the steps.
84 ÷ 3
_____
Answer: 28
Explanation:
STEPS:
A. Draw 3 circles to represent the divisor. Then use base-ten blocks to model 84. Show 84 as 8 tens and 4 ones.
B. Share the tens equally among the 3 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 3 groups.
D. There are 2 ten(s) and 8 one(s) in each group. So, the quotient is 28.

Question 5.
Explain why you did not need to regroup in Exercise 2.
Type below:
___________
Answer: We did not regroup in exercise two because we used the method of counters in which we placed the counters one after the other in the circles and concluded with number of counters in each group and the number of counters left over.
Explanation:
Example: 28 ÷ 3(in the form of exercise 2)
A. Use 28 counters to represent the 28 dominoes. Then draw 3 circles to represent the 3 players.
B. Share the counters equally among the 3 groups by placing them in the circles.
C. Find the number of counters in each group and the number of counters left over. Record your answer. 9 counters in each group and 3 counters are leftover.
Example: 84 ÷ 3
A. Draw 3 circles to represent the divisor. Then use base-ten blocks to model 84. Show 84 as 8 tens and 4 ones.
B. Share the tens equally among the 3 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 3 groups.
D. There are 2 ten(s) and 8 one(s) in each group. So, the quotient is 28.
Question 6.
Mindy is preparing fruit boxes for gifts. She divides 36 apples evenly into 6 boxes. Then she divided 54 bananas evenly into the same 6 boxes. How many pieces of fruit are in each of Mindy’s boxes?
_____ pieces of fruit
Answer: 6+9=15 pieces of fruits are in each box of Mindy’s
Explanation:
Total number of apples = 36
Number of boxes in which the apples were kept = 6
Number of apple pieces in each box = 36 ÷ 6 = 6
Total number of bananas = 54
Number of boxes in which the bananas were kept = 6
Number of banana pieces in each box = 54 ÷ 6 = 9
Total number of fruit pieces in each box = 9 + 6 = 15
Question 7.
Ami needs to divide these base-ten blocks into 4 equal groups.

Describe a model that would show how many are in each group.
Type below:
___________
Answer: 14
Explanation:
A. Draw 4 circles to represent the divisor. Then use base-ten blocks to model 56. Show 56 as 5 tens and 6 ones.
B. Share the tens equally among the 4 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 4 groups.
D. There are 1 ten(s) and 4 one(s) in each group. So, the quotient is 14.
Page No. 250
Sense or Nonsense?
Question 8.
Angela and Zach drew quick pictures to find 68 ÷ 4. Whose quick picture makes sense? Whose quick picture is nonsense? Explain your reasoning.
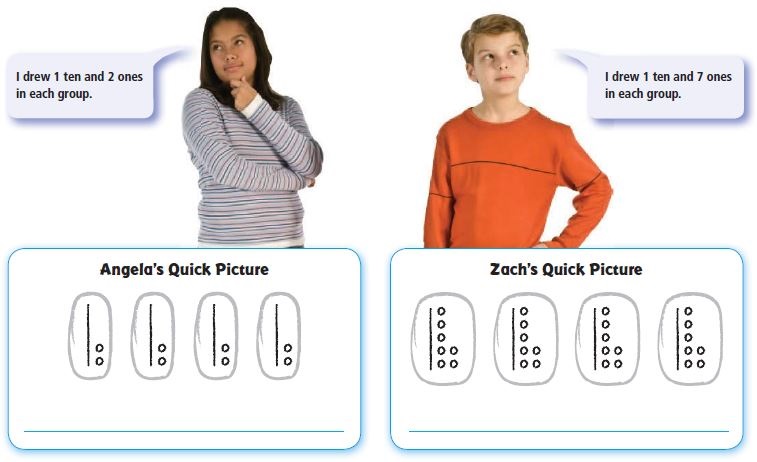
Type below:
___________
Answer: Zach’s quick picture is correct while Angela’s is not correct.
Explanation:
A. Draw 4 circles to represent the divisor. Then use base-ten blocks to model 68. Show 68 as 6 tens and 8 ones.
B. Share the tens equally among the 4 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 4 groups.
D. There are 1 ten(s) and 7 one(s) in each group. So, the quotient is 17.
Hence Zach’s statement and the quick picture are correct.
Question 9.
Analyze What did Angela forget to do after she shared the tens equally among the 4 groups?
Type below:
___________
Answer: Angela forgot to regroup the leftover tens into ones. Share the ones equally among the 4 groups.
Explanation:
Since there are 6 tens and 4 circles only 4 tens can be placed in them while the other 2 tens are leftover which must be converted into 20 ones.
Common Core – Page No. 251
Model Division with Regrouping
Divide. Use base-ten blocks.
Question 1.
63 ÷ 4 = 15 r3
Answer: 15 r 3
Explanation:
A. Draw 4 circles to represent the divisor. Then use base-ten blocks to model 63. Show 63 as 6 tens and 3 ones.
B. Share the tens equally among the 4 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 4 groups.
D. There are 1 ten(s) and 5 one(s) in each group. So, the quotient is 15.
E. After grouping, there are 3 blocks which weren’t grouped. So, the remainder is 3
Question 2.
83 ÷ 3
_____ R _____
Answer: 27 r 2
Explanation:
A. Draw 3 circles to represent the divisor. Then use base-ten blocks to model 83. Show 83 as 8 tens and 3 ones.
B. Share the tens equally among the 3 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 3 groups.
D. There are 2 ten(s) and 7 one(s) in each group. So, the quotient is 27.
E. After grouping, there are 2 blocks which weren’t grouped. So, the remainder is 2




Divide. Draw quick pictures. Record the steps.
Question 3.
85 ÷ 5
_____
Answer: 17
Explanation:
A. Draw 5 circles to represent the divisor. Then use base-ten blocks to model 85. Show 85 as 8 tens and 5 ones.
B. Share the tens equally among the 5 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 5 groups.
D. There are 1 ten(s) and 7 one(s) in each group. So, the quotient is 17.




Question 4.
97 ÷ 4
_____ R _____
Answer: 24 r 1
Explanation:
A. Draw 4 circles to represent the divisor. Then use base-ten blocks to model 97. Show 97 as 9 tens and 7 ones.
B. Share the tens equally among the 4 groups.
C. If there are any tens left, regroup them as ones. Share the ones equally among the 4 groups.
D. There are 2 ten(s) and 4 one(s) in each group. So, the quotient is 24.
E. After grouping, there is 1 block which wasn’t grouped. So, the remainder is 1




Problem Solving
Question 5.
Tamara sold 92 cold drinks during her 2-hour shift at a festival food stand. If she sold the same number of drinks each hour, how many cold drinks did she sell each hour?
_____ cold drinks
Answer: 46 cold drinks
Explanation:
Total number of cold drinks Tamara sold = 92
The time in which she sold the drinks = 2 hours
Number of drinks she sold in each hour = 92 ÷ 2 = 46
Question 6.
In 3 days Donald earned $42 running errands. He earned the same amount each day. How much did Donald earn from running errands each day?
$ _____
Answer: $14
Explanation:
Total amount earned by Donald = $42
Number of days = 3
Amount earned on each day = $42 ÷ 3 = $14
Common Core – Page No. 252
Lesson Check
Question 1.
Gail bought 80 buttons to put on the shirts she makes. She uses 5 buttons for each shirt. How many shirts can Gail make with the buttons she bought?
Options:
a. 14
b. 16
c. 17
d. 18
Answer: b. 16
Explanation:
Total number of buttons = 80
Number of buttons used for each shirt = 5
Number of shirts she can make = 80 ÷ 5 =16
Question 2.
Marty counted how many breaths he took in 3 minutes. In that time, he took 51 breaths. He took the same number of breaths each minute. How many breaths did Marty take in one minute?
Options:
a. 15
b. 16
c. 17
d. 19
Answer: c. 17
Explanation:
Total number of breaths Marty counted = 51
Time in which the breath was counted = 3 minutes
Number of breaths in one minute = 51 ÷ 3 = 17
Spiral Review
Question 3.
Kate is solving brain teasers. She solved 6 brain teasers in 72 minutes. How long did she spend on each brain teaser?
Options:
a. 12 minutes
b. 14 minutes
c. 18 minutes
d. 22 minutes
Answer: a. 12 minutes
Explanation:
Number of brain teasers solved = 6
Number of minutes spent on brain teasers = 72 minutes
Number of minutes spent on each problem = 72 ÷ 6 =12 minutes
Question 4.
Jenny works at a package delivery store. She puts mailing stickers on packages. Each package needs 5 stickers. How many stickers will Jenny use if she is mailing 105 packages?
Options:
a. 725
b. 625
c. 525
d. 21
Answer: c. 525
Explanation:
Number of packages = 105
Number of stickers on each package = 5
Total number of stickers on the packages = 105 x 5 = 525
Question 5.
The Puzzle Company packs standardsized puzzles into boxes that hold 8 puzzles. How many boxes would it take to pack up 192 standard-sized puzzles?
Options:
a. 12
b. 16
c. 22
d. 24
Answer: d. 24
Explanation:
Total number of puzzles = 192
Number of puzzles in each box = 8
Number of boxes used = 192 ÷ 8 = 24 boxes
Question 6.
Mt. Whitney in California is 14,494 feet tall. Mt. McKinley in Alaska is 5,826 feet taller than Mt. Whitney. How tall is Mt. McKinley?
Options:
a. 21,310 feet
b. 20,320 feet
c. 20,230 feet
d. 19,310 feet
Answer: b. 20,320 feet
Explanation:
Height of Mt. Whitney in California = 14,494 feet
Height of Mt. McKinley in Alaska is 5,826 feet taller than Mt. Whitney.
Therefore the height of Mt. McKinley in Alaska = 14,494 feet + 5,826 feet = 20,320 feet
Page No. 255
Question 1.
There are 452 pictures of dogs in 4 equal groups. How many pictures are in each group? Explain how you can use place value to place the first digit in the quotient.

______ pictures
Answer: 113
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 452. 400 hundred can be shared among 4 groups
without regrouping.
Now there is 1 ten to share among 4 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 45 ÷ 4
Multiply. 4 × 11 = 44
Subtract. 45 − 44 = 1 tens
STEP 3 Divide the ones.
Regroup 1 ten as 10 ones.
Now there are 12 ones to share among 4 groups.
Divide. 12 ones ÷ 4
Multiply. 4×3 ones
Subtract. 12 ones − 12 ones = 0
So, the quotient is 113
Divide.
Question 2.
4)\(\overline { 166 } \)
______ R ______
Answer: 41
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 166. 1 hundred cannot be shared among 4 groups
without regrouping.
Now there is 1 ten to share among 4 groups.
The first digit of the quotient will be in the tens place.
STEP 2 Divide the tens.
Divide. 166 ÷ 4
Multiply. 4 × 40 = 160
Subtract. 166 − 160 = 6
STEP 3 Divide the ones.
Now there are 6 ones to share among 4 groups.
Divide. 6 ones ÷ 4
Multiply. 4×1 ones
Subtract. 6 ones − 4 ones = 2
So, the quotient is 41 and remainder is 2
Question 3.
5)\(\overline { 775 } \)
______
Answer: 155
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 775. 700 hundred can be shared among 5 groups
without regrouping.
Now there is 70 ten to share among 5 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 700 ÷ 5
Multiply. 5 × 140 = 700
Subtract. 700 − 700 = 0
STEP 3 Divide the ones.
Now there are 70 tens to share among 5 groups.
Divide. 70 tens ÷ 5
Multiply. 5×14
Subtract. 75 − 70 tens = 5 ones
Multiply 5 x 1 = 5
Subtract 5 ÷ 5 = 0
So, the quotient is 155 (140 + 14 + 1)
Question 4.
4)\(\overline { 284 } \)
______
Answer: 71
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 284. 200 hundred can be shared among 4 groups
without regrouping.
Now there are 20 tens to share among 4 groups.
The first digit of the quotient will be in the tens place.
STEP 2 Divide the tens.
Divide. 200 ÷ 4
Multiply. 4 × 50 = 200
Subtract. 20 − 20 = 0 tens
STEP 3 Divide the ones.
Now there are 80 tens to share among 4 groups.
Divide. 80 tens ÷ 4
Multiply. 4×20 = 80
Subtract. 80 tens − 80 tens = 0 ones
There are 4 ones
Multiply 4 x 1 = 4
Subtract 4-4 =0
So, the quotient is 71 (50+20+1)
Question 5.
5)\(\overline { 394 } \)
______ R ______
Answer: 78
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 394. 300 hundred can be shared among 5 groups
without regrouping.
Now there is 30 ten to share among 5 groups.
The first digit of the quotient will be in the tens place.
STEP 2 Divide the tens.
Divide. 300 ÷ 5
Multiply. 5 × 60 = 300
Subtract. 300 − 300 = 0 tens
STEP 3 Divide the tens.
Now there are 9 tens to share among 5 groups.
Divide. 9 tens ÷ 5
Multiply. 5×18 tens
Subtract. 90 tens − 90 tens = 0 ones
There are 4 ones
4 is the remainder.
So, the quotient is 78(60+18)
Question 6.
3)\(\overline { 465 } \)
______
Answer: 155
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 465. 400 hundred can be shared among 3 groups
without regrouping.
Now there are 40 tens to share among 3 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 400 ÷ 3
Multiply. 3 × 130 = 390
Subtract. 400 − 390 = 1 tens
STEP 3 Divide the tens.
Now there are 7 tens and 5 ones to share among 3 groups.
Divide. 75 ÷ 3
Multiply. 3 × 25 = 75
Subtract. 75 tens − 75 tens = 0
So, the quotient is 155 ( 130+ 25)
Question 7.
8)\(\overline { 272 } \)
______
Answer: 34
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 272. 200 hundred can be shared among 8 groups
without regrouping.
Now there is 27 tens and 2 ones to share among 8 groups.
The first digit of the quotient will be in the tens place.
STEP 2 Divide the tens.
Divide. 270 ÷ 8
Multiply. 8 × 30 = 240
Subtract. 270 − 240 = 3 tens
STEP 3 Divide the ones.
Regroup 3 tens as 30 ones.
Now there are 30 + 2 = 32 ones to share among 8 groups.
Divide. 32 ones ÷ 8
Multiply. 8×4 ones
Subtract. 32 ones − 32 ones = 0
So, the quotient is 34 (30 + 4)
Practice: Copy and Solve Divide.
Question 8.
516 ÷ 2 = ______
Answer: 258
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 516. 500 hundred can be shared among 2 groups
without regrouping.
Now there is 50 tens and 16 ones to share among 2 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 500 ÷ 2
Multiply. 2 × 250 = 500
Subtract. 516 − 500 = 16 ones
STEP 3 Divide the ones.
Now there are 16 ones to share among 2 groups.
Divide. 16 ones ÷ 2
Multiply. 2×8 ones
Subtract. 16 ones − 16 ones = 0
So, the quotient is 258 (250 + 8)
Question 9.
516 ÷ 3 = ______
Answer: 172
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 516. 500 hundred can be shared among 3 groups
without regrouping.
Now there is 50 tens and 16 ones to share among 3 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 500 ÷ 3
Multiply. 3 × 160 = 480
Subtract. 516 − 480 = 36 ones
STEP 3 Divide the ones.
Now there are 36 ones to share among 3 groups.
Divide. 36 ones ÷ 3
Multiply. 3×12 ones
Subtract. 36 ones − 36 ones = 0
So, the quotient is 172 (160 + 12)
Question 10.
516 ÷ 4 = ______
Answer: 129
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 516. 500 hundred can be shared among 4 groups
without regrouping.
Now there is 50 tens and 16 ones to share among 4 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 500 ÷ 4
Multiply. 4 × 125 = 500
Subtract. 516 − 500 = 16 ones
STEP 3 Divide the ones.
Now there are 16 ones to share among 4 groups.
Divide. 16 ones ÷ 4
Multiply. 4×4 ones
Subtract. 16 ones − 16 ones = 0
So, the quotient is 129 (125 + 4)
Question 11.
516 ÷ 5 = ______ R ______
Answer: 103 R 1
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 516. 500 hundred can be shared among 5 groups
without regrouping.
Now there is 50 tens and 16 ones to share among 5 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 500 ÷ 5
Multiply. 5 × 100 = 500
Subtract. 516 − 500 = 16 ones
STEP 3 Divide the ones.
Now there are 16 ones to share among 5 groups.
Divide. 16 ones ÷ 5
Multiply. 5×3 ones
Subtract. 16 ones − 15 ones = 1 one
So, the quotient is 103 (100 + 3) and the remainder is 1
Question 12.
Look back at your answers to Exercises 8–11. What happens to the quotient when the divisor increases? Explain.
The quotient ______
Answer: The quotient gets decreased when we increase the divisor.
Explanation:
Example:
516 ÷ 4 = ______
Answer: 129
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 516. 500 hundred can be shared among 4 groups
without regrouping.
Now there is 50 tens and 16 ones to share among 4 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 500 ÷ 4
Multiply. 4 × 125 = 500
Subtract. 516 − 500 = 16 ones
STEP 3 Divide the ones.
Now there are 16 ones to share among 4 groups.
Divide. 16 ones ÷ 4
Multiply. 4×4 ones
Subtract. 16 ones − 16 ones = 0
So, the quotient is 129 (125 + 4)
516 ÷ 5 = ______ R ______
Answer: 103 R 1
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 516. 500 hundred can be shared among 5 groups
without regrouping.
Now there is 50 tens and 16 ones to share among 5 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 500 ÷ 5
Multiply. 5 × 100 = 500
Subtract. 516 − 500 = 16 ones
STEP 3 Divide the ones.
Now there are 16 ones to share among 5 groups.
Divide. 16 ones ÷ 5
Multiply. 5×3 ones
Subtract. 16 ones − 15 ones = 1 one
So, the quotient is 103 (100 + 3) and the remainder is 1
Question 13.
Reggie has 192 pictures of animals. He wants to keep half and then divide the rest equally among three friends. How many pictures will each friend get?
______ pictures
Answer: 32
Explanation:
Total number of animal pictures = 192
Number of animal pictures he kept with him = 192 ÷ 2 = 96
Number of pictures each of his friends got = 96 ÷ 3 = 32 pictures
Question 14.
There are 146 students, 5 teachers, and 8 chaperones going to the theater. To reserve their seats, they need to reserve entire rows. Each row has 8 seats. How many rows must they reserve?
______ rows
Answer: 20 rows
Explanation:
Total people who went to the theatre = 146 + 5 + 8 = 159
Number of seats in each row = 8
Number of rows which must be reserved for the students = 159 ÷ 8 =19.8 = 20 (approx)
Page No. 256
Question 15.
Nan wants to put 234 pictures in an album with a blue cover. How many full pages will she have in her album?

a. What do you need to find?
Type below:
_________
Answer: How many full pages will she have in her album?
We can find number of pictures in blue pages?
We can find number of pictures in green pages?
We can find number of pictures in red pages?
Explanation:
Question 15.
b. How will you use division to find the number of full pages?
Type below:
_________
Answer: Since the total number of pictures and the number of colour pages are given we can divide the total number of pictures are the number of pages to find the number of full pages.
Explanation:
Total number of pictures =234
Number of pictures per page = 4 + 6+ 8 = 18
Number of full pages = 234 ÷ 18 =13
Question 15.
c. Show the steps you will use to solve the problem.
Type below:
_________
Answer: 13
Explanation:
Total number of pictures =234
Number of pictures per page = 4 + 6+ 8 = 18
Number of full pages = 234 ÷ 18 =13
Question 15.
d. Complete the following sentences.
Nan has _______ pictures.
She wants to put the pictures in an album with pages that each hold _______ pictures.
She will have an album with _______ full pages and _______ pictures on another page.
Type below:
_________
Answer: 234 pictures, 18 pictures, 13 full pages, 0 pictures on another page
Explanation:
Total number of pictures =234
Number of pictures per page = 4 + 6+ 8 = 18
Number of full pages = 234 ÷ 18 =13 full pages
Since the remainder is 0 the number of pictures on another page = 0
Question 16.
Mr. Parsons bought 293 apples to make pies for his shop. Six apples are needed for each pie. If Mr. Parsons makes the greatest number of apple pies possible, how many apples will be left?
_____ pies _____ apples left over.
Answer: 48 pies and 5 apples are leftover
Explanation:
Total number of apples= 293
Number of apples that make a pie = 6
Number of pies = Quotient of 293 ÷ 6 = 48
Number of apples leftover = 5
Question 17.
Carol needs to divide 320 stickers equally among 4 classes. In which place is the first digit of the quotient? Choose the word that completes the sentence.
The first digit of the quotient is in the  place.
place.
_________
Answer: tens
Explanation:
Total number of stickers = 320
Number of classes = 4
Number of stickers in each class = Quotient of 320 ÷ 4 = 80
The first digit of quotient is in the tens place.
Common Core – Page No. 257
Place the First Digit
Divide.
Question 1.
62
——-
3)\(\overline { 186 } \)
-18
——-
06
-6
——-
0
Answer: 62
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 186. 180 hundred can be shared among 3 groups
without regrouping.
Now there is 18 tens and 6 ones to share among 3 groups.
The first digit of the quotient will be in the tens place.
STEP 2 Divide the tens.
Divide. 180 ÷ 3
Multiply. 3 × 60 = 180
Subtract. 186 − 180 = 6 ones
STEP 3 Divide the ones.
Now there are 6 ones to share among 3 groups.
Divide. 6 ones ÷ 3
Multiply. 2×3 ones
Subtract. 6 ones − 2 ones =0 one
So, the quotient is 62 (60 + 2) and the remainder is 0
Question 2.
4)\(\overline { 298 } \)
_____ R _____
Answer:
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 298. 280 hundred can be shared among 4 groups
without regrouping.
Now there is 28 tens and 18 ones to share among 4 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 280 ÷ 4
Multiply. 4 × 70 = 280
Subtract. 280 − 280 = 0 ones
STEP 3 Divide the ones.
Now there are 18 ones to share among 4 groups.
Divide. 18 ones ÷ 4
Multiply. 4×4 ones
Subtract. 18 ones − 16 ones = 2 ones
So, the quotient is 74 (70 + 4) and the remainder is 2
Question 3.
3)\(\overline { 461 } \)
_____ R _____
Answer: 153
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 461. 450 hundred can be shared among 3 groups
without regrouping.
Now there is 45 tens and 11 ones to share among 3 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 450 ÷ 3
Multiply. 3 × 150 = 450
Subtract. 450 − 450 = 0 ones
STEP 3 Divide the ones.
Now there are 11 ones to share among 3 groups.
Divide. 11 ones ÷ 3
Multiply. 3×3 ones
Subtract. 11 ones − 9 ones = 2 ones
So, the quotient is 153 (150 + 3) and the remainder is 2
Question 4.
9)\(\overline { 315 } \)
_____ R _____
Answer: 35
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 315. 310 hundred can be shared among 9 groups
without regrouping.
Now there is 31 tens and 5 ones to share among 9 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide.310 ÷ 9
Multiply. 9 × 30 = 270
Subtract. 310 − 270 = 40 ones
STEP 3 Divide the ones.
Now there are 40 + 5 = 45 ones to share among 9 groups.
Divide. 45 ones ÷ 9
Multiply. 5×9 ones
Subtract. 45 ones − 45 ones = 0 ones
So, the quotient is 35 (30 + 5) and the remainder is 0
Question 5.
2)\(\overline { 766 } \)
_____ R _____
Answer: 383
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 766. 760 hundred can be shared among 2 groups
without regrouping.
Now there is 76 tens and 6 ones to share among 2 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 760 ÷ 2
Multiply. 2 × 380 = 760
Subtract. 760 − 760 = 0 ones
STEP 3 Divide the ones.
Now there are 6 ones to share among 2 groups.
Divide. 6 ones ÷ 2
Multiply. 2×3 ones
Subtract. 6 ones − 6 ones = 0 ones
So, the quotient is 383 (380 + 3) and the remainder is 0
Question 6.
4)\(\overline { 604 } \)
_____ R _____
Answer: 151
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 604. 600 hundred can be shared among 4 groups
without regrouping.
Now there is 60 tens and 4 ones to share among 4 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 600 ÷ 4
Multiply. 4 × 150 = 600
Subtract. 600 − 600 = 0 ones
STEP 3 Divide the ones.
Now there are 4 ones to share among 4 groups.
Divide. 4 ones ÷ 4
Multiply. 4×1 ones
Subtract. 4 ones − 4 ones = 0 ones
So, the quotient is 151 (150 + 1) and the remainder is 0
Question 7.
6)\(\overline { 796 } \)
_____ R _____
Answer: 132
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 796. 790 hundred can be shared among 6 groups
without regrouping.
Now there is 79 tens and 6 ones to share among 6 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 790 ÷ 6
Multiply. 6 × 131 = 786
Subtract. 790 − 786 = 4 ones
STEP 3 Divide the ones.
Now there are 4 + 6 = 10 ones to share among 6 groups.
Divide. 10 ones ÷ 6
Multiply. 6×1 ones
Subtract. 10 ones − 6 ones = 4 ones
So, the quotient is 132 (131 + 1) and the remainder is 4
Question 8.
5)\(\overline { 449 } \)
_____ R _____
Answer: 89
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 449. 440 hundred can be shared among 5 groups
without regrouping.
Now there is 44 tens and 9 ones to share among 5 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 440 ÷ 5
Multiply. 5 × 88 = 440
Subtract. 440 − 440 = 0 ones
STEP 3 Divide the ones.
Now there are 9 ones to share among 5 groups.
Divide. 9 ones ÷ 5
Multiply. 5×1 ones
Subtract. 9 ones − 5 ones = 4 ones
So, the quotient is 89 (88 + 1) and the remainder is 4
Question 9.
6)\(\overline { 756 } \)
_____ R _____
Answer: 126
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 756. 750 hundred can be shared among 6 groups
without regrouping.
Now there is 75 tens and 6 ones to share among 6 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 750 ÷ 6
Multiply. 6 × 125 = 750
Subtract. 750 − 750 = 0 ones
STEP 3 Divide the ones.
Now there are 6 ones to share among 6 groups.
Divide. 6 ones ÷ 6
Multiply. 6×1 ones
Subtract. 6 ones − 6 ones = 0 ones
So, the quotient is 126 (125 + 1) and the remainder is 0
Question 10.
7)\(\overline { 521 } \)
_____ R _____
Answer: 74
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 521. 520 hundred can be shared among 7 groups
without regrouping.
Now there is 52 tens and 1 one to share among 7 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 520 ÷ 7
Multiply. 7 × 74 = 518
Subtract. 520 − 518 = 2 ones
STEP 3 Divide the ones.
Now there are 2 + 1 = 3 ones to share among 7 groups.
Divide. 3 ones ÷ 7 (not possible)
So, the quotient is 74 and the remainder is 3
Question 11.
5)\(\overline { 675 } \)
_____ R _____
Answer: 135
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 675. 670 hundred can be shared among 5 groups
without regrouping.
Now there is 67 tens and 5 ones to share among 5 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 670 ÷ 5
Multiply. 5 × 134 = 670
Subtract. 670 − 670 = 0 ones
STEP 3 Divide the ones.
Now there are 5 ones to share among 5 groups.
Divide. 5 ones ÷ 5
Multiply. 5×1 ones
Subtract. 5 ones − 5 ones = 0 ones
So, the quotient is 135 (134 + 1) and the remainder is 0
Question 12.
8)\(\overline { 933 } \)
_____ R _____
Answer: 116
Explanation:
STEP 1 Use place value to place the first digit. Look at the hundreds in 933. 930 hundred can be shared among 8 groups
without regrouping.
Now there is 93 tens and 3 ones to share among 8 groups.
The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the tens.
Divide. 930 ÷ 8
Multiply. 8 × 116 = 928
Subtract. 930 − 928 = 2 ones
STEP 3 Divide the ones.
Now there are 2 + 3 = 5 ones to share among 8 groups.
Divide. 5 ones ÷ 8 (not possible)
So, the quotient is 116 (100 + 3) and the remainder is 5
Problem Solving
Question 13.
There are 132 projects in the science fair. If 8 projects can fit in a row, how many full rows of projects can be made? How many projects are in the row that is not full?
_____ full rows
_____ projects in the non-full row
Answer: 16 full rows and 4 projects in the non-full row
Explanation:
Total number of projects = 132
Number of projects placed in full row = 8
Number of rows having full projects =Quotient of 132 ÷ 8 = 16
Number of projects in the non-full row = Remainder of 132 ÷ 8 = 4
Question 14.
There are 798 calories in six 10-ounce bottles of apple juice. How many calories are there in one 10-ounce bottle of apple juice?
_____ R _____ calories in one 10-ounce bottles of juice
Answer: 133 calories
Explanation:
Number of calories in 6 bottles of apple juice = 798
Number of calories in each bottle = 798 ÷6 = 133 calories
Common Core – Page No. 258
Lesson Check
Question 1.
To divide 572 ÷ 4, Stanley estimated to place the first digit of the quotient. In which place is the first digit of the quotient?
Options:
a. ones
b. tens
c. hundreds
d. thousands
Answer: c. hundreds
Explanation:
The quotient of 572÷ 4 is 143
STEP 1 Use place value to place the first digit. Look at the hundreds in 572. 560 hundred can be shared among 4 groups
without regrouping.
Now there is 1 ten to share among 4 groups.
The first digit of the quotient will be in the hundreds place.
Question 2.
Onetta biked 325 miles in 5 days. If she biked the same number of miles each day, how far did she bike each day?
Options:
a. 1,625 miles
b. 320 miles
c. 65 miles
d. 61 miles
Answer: c. 65 miles
Explanation:
Total number of miles biked = 325 miles
Number of days biked = 5
Number of miles biked on each day = Quotient of 325 ÷ 5 = 65
Spiral Review
Question 3.
Mort makes beaded necklaces that he sells for $32 each. About how much will Mort make if he sells 36 necklaces at the local art fair?
Options:
a. $120
b. $900
c. $1,200
d. $1,600
Answer: c. $1,200
Explanation:
Cost of each beaded necklace = $32
Number of necklaces = 36
The total cost of the necklaces = $32 x 36 = $1,200 (approx)
Question 4.
Which is the best estimate of 54 × 68?
Options:
a. 4,200
b. 3,500
c. 3,000
d. 350
Answer: b. 3,500
Explanation:
Taking the terms nearest to the 54 x 68 as 54 x 65 = 3510 = 3500 (approx)
Question 5.
Ms. Eisner pays $888 for 6 nights in a hotel. How much does Ms. Eisner pay per night?
Options:
a. $5,328
b. $882
c. $148
d. $114
Answer: c. $148
Explanation:
Total pays of Ms Eisner in a hotel = $888
Number of nights = 6
Amount Ms Eisner pay per night = $888 ÷ 6 = $148
Question 6.
Which division problem does the model show?

Options:
a. 42 ÷ 3
b. 44 ÷3
c. 51 ÷ 3
d. 54 ÷ 3
Answer: d. 54 ÷ 3
Explanation:
Number of counters in each model = 18
Number of models = 3
Total number of counters = 18 x 3 = 54
Therefore the model displays = 54 ÷ 3
Page No. 261
Question 1.
Ollie used 852 beads to make 4 bracelets. He put the same number of beads on each bracelet. How many beads does each bracelet have? Check your answer.

Divide Check
2
4)\(\overline { 852 } \)
So, each bracelet has _____ beads.
_____ beads
Answer: 213
Explanation:
Total number of beads =852
Number of bracelets = 4
Number of beads in each bracelet = 852 ÷ 4 = 213

Divide and check.
Question 2.
2)\(\overline { 394 } \)
_____
Answer: 197
Explanation:
STEP 1 Use place value to place the first digit. The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the hundreds.
STEP 3 Divide the tens.
STEP 4 Divide the ones.

Question 3.
2)\(\overline { 803 } \)
_____ R _____
Answer: 401 R 1
Explanation:
STEP 1 Use place value to place the first digit. The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the hundreds.
STEP 3 Divide the tens.
STEP 4 Divide the ones.

Question 4.
3)\(\overline { 3,448 } \)
_____ R _____
Answer: 1149 R 1
Explanation:
STEP 1 Use place value to place the first digit. Look at the thousands in 3,448. 3 thousand can be shared among 3 groups without regrouping. The first digit of the quotient will be in the thousands place.
STEP 2 Divide the thousands.
STEP 3 Divide the hundreds.
STEP 4 Divide the tens.
STEP 5 Divide the ones.

Question 5.
2)\(\overline { 816 } \)
_____
Answer: 408
Explanation:
STEP 1 Use place value to place the first digit. The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the hundreds.
STEP 3 Divide the tens.
STEP 4 Divide the ones.

Question 6.
4)\(\overline { 709 } \)
_____ R _____
Answer: 177 R 1
Explanation:
STEP 1 Use place value to place the first digit. The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the hundreds.
STEP 3 Divide the tens.
STEP 4 Divide the ones.

Question 7.
3)\(\overline { 267 } \)
_____
Answer: 89
Explanation:
STEP 1 Use place value to place the first digit. The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the hundreds.
STEP 3 Divide the tens.
STEP 4 Divide the ones.

Question 8.
The flower shop received a shipment of 248 pink roses and 256 red roses. The shop owner uses 6 roses to make one arrangement. How many arrangements can the shop owner make if he uses all the roses?
_____ arrangement
Answer: 84 arrangements
Explanation:
Number of pink roses = 248
Number of red roses = 256
Total number of roses = 504
Number of roses in each arrangement = 6
Number of arrangements = 504 ÷ 6 = 84
Page No. 262
Use the table for 9–11.

Question 9.
Four teachers bought 10 origami books and 100 packs of origami paper for their classrooms. They will share the cost of the items equally. How much should each teacher pay?
_____ $
Answer: $210
Explanation:
Number of origami books = 10
Cost of each origami book = $24
Total cost of origami books = $24 x 10 = $240
Number of origami papers = 100
Cost of each origami book = $6
Total cost of origami books = $6 x 100 = $600
Total cost of items = $240 + $600 = $840
Number of teachers = 4
Cost earned by each teacher = $840 ÷ 4 = $210
Question 10.
Communicate Six students shared equally the cost of 18 of one of the items in the chart. Each student paid $24. What item did they buy? Explain how you found your answer.
__________
Answer: The students bought origami kit.
Explanation:
Number of students = 6
Number of items they bought = 18
Amount each student paid = $24
The total amount paid = $24 x 6 =$144
The item they bought can be found by knowing the cost of the item:
Cost of the item=
The total amount paid ÷ Number of items = 144 ÷ 18 = $8
Therefore the item is origami kit.
Question 11.
Ms Alvarez has $1,482 to spend on origami paper. How many packs can she buy?
_____ packs
Answer: 247
Explanation:
Cost of origami paper = $6
Amount Ms Alvarez was supposed to spend on origami paper = $1,482
Number of packs bought = $1,482 ÷ $6 = 247
Question 12.
Evan made origami cranes with red, blue, and yellow paper. The number of cranes in each color is the same. If there are 342 cranes, how many of them are blue or yellow?
_____ blue, or yellow
Answer: 114
Explanation:
Evan made origami cranes with red, blue, and yellow paper.
The number of cranes in each colour is the same.
Total number of cranes = 342
Number of cranes of each colour = 342 ÷ 3 = 114
Therefore there are 114 cranes of blue and yellow.
Question 13.
On Monday 336 fourth graders went on a field trip to a local park. The teachers divided the students into 8 groups.
Use a basic fact. Estimate the number of students in each group. Show your work.
_____ about
Answer: 42
Explanation:
Total number who went to the field trip = 336
Number of groups into which they were divided = 8 groups
Number of students in each group = 336 ÷ 8 = 42 students
Common Core – Page No. 263
Divide by 1-Digit Numbers
Divide and check.
Question 1.
318
2)\(\overline { 636 } \) 318
-6 × 2
—— ——-
03 636
-2
——
16
-16
——-
0
Answer: 318
Explanation:
STEP 1 Use place value to place the first digit. The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the hundreds.
STEP 3 Divide the tens.
STEP 4 Divide the ones.

Question 2.
4)\(\overline { 631 } \)
_____ R _____
Answer:
Explanation:
STEP 1 Use place value to place the first digit. The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the hundreds.
STEP 3 Divide the tens.
STEP 4 Divide the ones.

Question 3.
8)\(\overline { 906 } \)
_____ R _____
Answer:
Explanation:
STEP 1 Use place value to place the first digit. The first digit of the quotient will be in the hundreds place.
STEP 2 Divide the hundreds.
STEP 3 Divide the tens.
STEP 4 Divide the ones.

Question 4.
6)\(\overline { 6,739 } \)
_____ R _____
Answer:
Explanation:
STEP 1 Use place value to place the first digit. Look at the thousands in 6,739. 6 thousand can be shared among 6 groups without regrouping. The first digit of the quotient will be in the thousands place.
STEP 2 Divide the thousands.
STEP 3 Divide the hundreds.
STEP 4 Divide the tens.
STEP 5 Divide the ones.

Question 5.
4)\(\overline { 2,328 } \)
_____ R _____
Answer:
Explanation:
STEP 1 Use place value to place the first digit. Look at the thousands in 2,328. 2 thousand can be shared among 4 groups without regrouping. The first digit of the quotient will be in the thousands place.
STEP 2 Divide the thousands.
STEP 3 Divide the hundreds.
STEP 4 Divide the tens.
STEP 5 Divide the ones.

Question 6.
5)\(\overline { 7,549 } \)
_____ R _____
Answer:
Explanation:
STEP 1 Use place value to place the first digit. Look at the thousands in 7,549. 7 thousand can be shared among 5 groups without regrouping. The first digit of the quotient will be in the thousands place.
STEP 2 Divide the thousands.
STEP 3 Divide the hundreds.
STEP 4 Divide the tens.
STEP 5 Divide the ones.

Problem Solving
Use the table for 7 and 8.
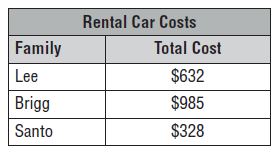
Question 7.
The Briggs rented a car for 5 weeks. What was the cost of their rental car per week?
$ _____
Answer: $197
Explanation:
Cost of the car of Briggs = $985
Number of weeks = 5
Cost of rent per week = $985 ÷ 5 =$ 197
Question 8.
The Lees rented a car for 4 weeks. The Santos rented a car for 2 weeks. Whose weekly rental cost was lower? Explain.
The rental cost of _____
Answer: Weekly rental cost was lower for Lees compared to Santos
Explanation:
Cost of the car of Lees = $632
Number of weeks = 4
Cost of rent per week = $632 ÷ 4 =$ 158
Cost of the car of Santos = $328
Number of weeks = 2
Cost of rent per week = $328 ÷ 2 =$ 164
Therefore weekly rental cost was lower for Lees compared to Santos.
Common Core – Page No. 264
Lesson Check
Question 1.
Which expression can be used to check
the quotient 646 ÷ 3?
Options:
a. (251 × 3) + 1
b. (215 × 3) + 2
c. (215 × 3) + 1
d. 646 × 3
Answer: c. (215 × 3) + 1
Explanation:
Multiply 215 x 3 = 645
Then add 1 to 645
Then the dividend is 645 + 1 = 646
Question 2.
There are 8 volunteers at the telethon. The goal for the evening is to raise $952. If each volunteer raises the same amount, what is the minimum amount each needs to raise to meet the goal?
Options:
a. $7,616
b. $944
c. $119
d. $106
Answer: a. $7,616
Explanation:
Number of volunteers = 8
Amount raised by each volunteer = $952
Total amount raised = $952 x 8 = $7,616
Spiral Review
Question 3.
Which product is shown by the model?
Options:
a. 5 × 15 = 75
b. 5 × 16 = 80
c. 5 × 17 = 75
d. 5 × 17 = 85
Answer: d. 5 × 17 = 85
Explanation:
By counting the number of counters we can give the expression.
Number of counters in one row = 17
Number of rows = 5
Therefore the expression = 5 × 17 = 85
Question 4.
The computer lab at a high school ordered 26 packages of CDs. There were 50 CDs in each package. How many CDs did the computer lab order?
Options:
a. 1,330
b. 1,300
c. 1,030
d. 130
Answer: b. 1,300
Explanation:
Number of packages = 26
Number of CDs in each pack = 50
Total number of CDs the computer lab ordered = 26 x 50 = 1,300
Question 5.
Which of the following division problems has a quotient with the first digit in the hundreds place?
Options:
a. 892 ÷ 9
b. 644 ÷ 8
c. 429 ÷ 5
d. 306 ÷ 2
Answer: d. 306 ÷ 2
Explanation:
Use place value to place the first digit. Look at the hundreds in 306. 300 hundred can be shared among 2 groups
without regrouping.
Now there is 30 tens and 6 ones to share among 2 groups.
The first digit of the quotient will be in the hundreds place.
Question 6.
Sharon has 64 ounces of juice. She is going to use the juice to fill as many 6-ounce glasses as possible. She will drink the leftover juice. How much juice will Sharon drink?
Options:
a. 4 ounces
b. 6 ounces
c. 10 ounces
d. 12 ounces
Answer: a. 4 ounces
Explanation:
The total quantity of juice = 64 ounces
Quantity of juice she filled = 6 ounces
Quantity of juice she drank = Remainder of 64 ÷ 6 = 4

Page No. 267
Question 1.
A firehouse pantry has 52 cans of vegetables and 74 cans of soup. Each shelf holds 9 cans. What is the least number of shelves needed for all the cans?
First, draw a bar model for the total number of cans.
Next, add to find the total number of cans.
Then, draw a bar model to show the number of shelves needed.
Finally, divide to find the number of shelves needed.
So, _______ shelves are needed to hold all of the cans.
_______ shelves
Answer: 14
Explanation:
Number of vegetable cans = 52






Number of soup cans = 74








Total number of cans = 74 +52 = 126
126 ÷ 9 = 14

So, 14 shelves are needed to hold all of the cans.
Question 2.
What if 18 cans fit on a shelf? What is the least number of shelves needed? Describe how your answer would be different.
_______ shelves
Answer: 7 shelves
Explanation:
Total number of cans = 126
Number of cans which can fit in one shelf = 18
Number of shelves required to place all the cans = 126 ÷ 18 = 7 shelves
Question 3.
Julio’s dad bought 10 dozen potatoes. The potatoes were equally divided into 6 bags. How many potatoes are in each bag?
_______ potatoes
Answer: 20 potatoes
Explanation:
Total number of potatoes = 10 dozens x 12 = 120
Number of bags = 6
Number of potatoes in each bag = 120 ÷ 6 = 20
Question 4.
At the garden shop, each small tree costs $125 and each large tree costs $225. How much will 3 small trees and 1 large tree cost?
$ _______
Answer: $600
Explanation:
Number of small trees = 3
Cost of each small tree = $125
Total cost of the small trees = $125 x 3 = $375
Number of large trees = 1
Cost of each large tree = $225
Total cost of the plants = $375 + $225 = $600
Page No. 268
Question 5.
Ms Johnson bought 6 bags of balloons. Each bag has 25 balloons. She fills all the balloons and puts 5 balloons in each bunch. How many bunches can she make?
_______ bunches
Answer: 30
Explanation:
Number of bags = 6
Number of ballons in each bag = 25
Total number of ballons = 25 x 6 = 150
Number of ballons in each bunch = 5
Number of bunches = Total number of ballons ÷ Number of ballons in each bunch = 150 ÷ 5 = 30
Question 6.
An adult’s dinner costs $8. A family of 2 adults and 2 children pays $26 for their dinners. How much does a child’s dinner cost? Explain.
$ _______
Answer: $10
Explanation:
Number of adults = 2
Number of children = 2
Cost of dinner of an adult = $8
The total cost of dinner of the adults = $8 x 2 = $16
Total amount paid = $26
Amount spent on children dinner = $26 – $16 = $10
Cost of dinner for the diner = $10 ÷ 2 = $5
Question 7.
Communicate Use the table at the right. Maria bought 80 ounces of apples. She needs 10 apples to make a pie. How many apples will be left over? Explain.
_______ apples
Answer: 6
Explanation:
Given the average weight of the apples = 5 ounces
Mass of apples Maria bought = 80 ounces
Number of apples = Mass of apples Maria bought ÷ average weight of the apples = 80 ÷ 5 = 16
Number of apples which make a pie = 10
Number of apples leftover = 16 – 10 = 6
Question 8.
Taylor has 16 tacks. She buys 2 packages of 36 tacks each. How many garage sale posters can she put up if she uses 4 tacks for each poster?
_______ posters
Answer: 18
Explanation:
Number of packages = 2
Number of posters in each package = 36
Total number of tacks = 36 x 2 = 72
Number of tacks for each poster = 4
Number of garage sale posters = 72 ÷ 4 = 18
Question 9.
Ryan bought 8 dozen bandages for the track team first-aid kit. The bandages were divided equally into 4 boxes. How many bandages are in each box?
_______ bandages
Answer: 24
Explanation:
Number of bandages bought for the track team first-aid kit = 8 dozens x 12 = 96
Number of boxes = 4
Number of bandages in each box = 96 ÷ 4 = 24
Common Core – Page No. 269
Problem Solving Multistep Division Problems
Solve. Draw a diagram to help you.
Question 1.
There are 3 trays of eggs. Each tray holds 30 eggs. How many people can be served if each person eats 2 eggs?

Think: What do I need to find? How can I draw a diagram to help?
45 people can be served
Answer: 45 people can be served.
Explanation:
Drawbar models to visualize the information given.
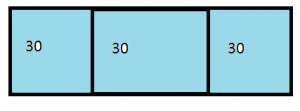
First, draw the model and compare to find the number of eggs they had.
Then we must model and divide to find how many eggs are served to each person.

Question 2.
There are 8 pencils in a package. How many packages will be needed for 28 children if each child gets 4 pencils?
________ packages
Answer: 14 packages
Explanation:
Number of pencils in each package = 8
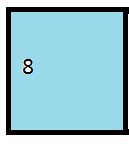
Number of children = 28
![]()
Number of pencils each child needs = 4
Total number of pencils = 28 x 4 =112
Number of packages = 112 ÷ 8 = 14
Question 3.
There are 3 boxes of tangerines. Each box has 93 tangerines. The tangerines will be divided equally among 9 classrooms. How many tangerines will each classroom get?
________ tangerines
Answer:31
Explanation:
Number of boxes = 3
Number of tangerines in each box = 93
Total number of tangerines = 93 x 3 = 279
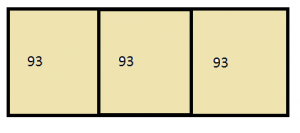
Number of classrooms = 9
Number of tangerines in each classroom = 279 ÷ 9 = 31
Question 4.
Misty has 84 photos from her vacation and 48 photos from a class outing. She wants to put all the photos in an album with 4 photos on each page. How many pages does she need?
______ pages
Answer: 33
Explanation:
Number of photos from her vacation = 84









Number of photos from her class outing = 48






Total number of photos = 84 + 48 = 132
Number of photos in each page = 4
Number of pages required = 132 ÷ 4 = 33
Common Core – Page No. 270
Lesson Check
Question 1.
Gavin buys 89 blue pansies and 86 yellow pansies. He will plant the flowers in 5 rows with an equal number of plants in each row. How many plants will be in each row?
Options:
a. 875
b. 175
c. 35
d. 3
Answer: c. 35
Explanation:
Number of blue pansies = 89
Number of yellow pansies = 86
Total number of pansies = 89 + 86 = 175
Number of rows = 5
Number of plants in each row = 175 ÷ 5 = 35
Question 2.
A pet store receives 7 boxes of cat food. Each box has 48 cans. The store wants to store the cans in equal stacks of 8 cans. How many stacks can be formed?
Options:
a. 8
b. 42
c. 56
d. 336
Answer: b. 42
Explanation:
Number of boxes of cat food = 7
Number of cans in a box = 48
Total number of cans = 48 x 7 = 336
Number of cans in each stack = 8
Number of stacks = 336 ÷ 8 = 42
Spiral Review
Question 3.
What product does the model show?

Options:
a. 284
b. 304
c. 340
d. 364
Answer: d. 364
Explanation:
Length = 20 +6 = 26
Breadth = 10 + 4 = 14
Area of the rectangle = 26 x 14 = 364
Question 4.
Mr. Hatch bought 4 round-trip airplane tickets for $417 each. He also paid $50 in baggage fees. How much did Mr. Hatch spend?
Options:
a. $467
b. $1,698
c. $1,718
d. $16,478
Answer: c. $1,718
Explanation:
Cost of each ticket of the airplane = $417
Cost baggage fees = $50
Number of trips of the airplane = 5
Cost of the trips = $417 x 5 = $1,668
The total cost of the trip = $1,668 + $50 = $1,718
Question 5.
Mae read 976 pages in 8 weeks. She read the same number of pages each week. How many pages did she read each week?
Options:
a. 109
b. 120
c. 122
d. 984
Answer: c. 122
Explanation:
Total number of pages = 976
Number of weeks = 8
Number of pages Mae read in each week = 976 ÷ 8 = 122
Question 6.
Yolanda and her 3 brothers shared a box of 156 toy dinosaurs. About how many dinosaurs did each child get?
Options:
a. 40
b. 50
c. 60
d. 80
Answer: b. 50
Explanation:
Total number of toy dinosaurs = 156
Number of brothers = 3
Number of toy dinosaurs each brother got = 156 ÷ 3 = 50
Page No. 271
Question 1.
There are 9 showings of a film about endangered species at the science museum. A total of 459 people saw the film. The same number of people were at each showing. About how many people were at each showing? Select the numbers the quotient is between.

Options:
A. 40
B. 50
C. 60
D. 70
E. 80
Answer: B. 50 C. 60 The quotient is between 50 and 60
Explanation:
Number of people at the showings = 459
Number of showings of a film = 9
Number of people at each showing = Quotient of 459 ÷ 9 = 51

Question 2.
Between which two numbers is the quotient of 87 ÷ 5? Write the numbers in the boxes.

The quotient is between _____ and _____.
Answer: The quotient is between 15 and 20.
Explanation:

Therefore the quotient is 17 and the remainder is 2.
Question 3.
Look at the model. What division does it show?
_____ ÷ _____ = _____ r _____
Answer: 19 ÷ 3 = 6 r 1
Explanation:
Count the total number of counters =Dividend = 19
Number of circles = Divisor = 3
After the distribution of the counters,
The quotient is 6 because in each circle there are 6 counters
The leftover counter is the remainder = 1
For 4a–4d, choose Yes or No to tell whether the division sentence has a remainder.
Question 4.
a. 28 ÷ 4
i. yes
ii. no
Answer: ii. no
Explanation:

Therefore the quotient is 7 and the remainder is 0
Question 4.
b. 35 ÷ 2
i. yes
ii. no
Answer: i. yes
Explanation:

Therefore the quotient is 17 and the remainder is 1
Question 4.
c. 40 ÷ 9
i. yes
ii. no
Answer: i. yes
Explanation:

Therefore the quotient is 4 and the remainder is 4
Question 4.
d. 45 ÷ 5
i. yes
ii. no
Answer: ii. no
Explanation:

Therefore the quotient is 5 and the remainder is 0
Page No. 272
Question 5.
A park guide plans the swan boat rides for 40 people. Each boat can carry 6 people at a time. What is the best way to interpret the remainder in this situation so that everyone gets a ride?
Type below:
____________
Answer: 4 people are leftover after the boat takes 6 people at a time for a ride, therefore, these four people go on the ride in the next round.
Explanation:
Quotient:
A. Use 40 counters to represent the 40 people. Then draw 6 circles to represent the divisor.
B. Share the counters equally among the 6 groups by placing them in the circles.
C. Number of counters formed in each group = quotient of 40 ÷ 6
D. Number of circles are equally filled with 6 counters, therefore, the quotient is 6
Therefore, the quotient is 6 and the remainder is 4
It means that the boat takes 7 rounds in which 6 are filled with 6 people while 4 people are leftover they take the last ride.
Question 6.
Nolan divides his 88 toy cars into boxes. Each box holds 9 cars. How many boxes does Nolan need to store all of his cars?
______ boxes
Answer: 10
Explanation:
Total number of toys Nolan has = 88
Number of cars placed in each box = 9
Number of boxes = 88 ÷ 9 = 9.7 = 10 (approx)
We take approximate value because all the toys must be fit in the box.
A group of 140 tourists are going on a tour. The tour guide rents 15 vans. Each van holds 9 tourists.
Question 7.
Part A
Write a division problem that can be used to find the number of vans needed to carry the tourists. Then solve.
Type below:
____________
Answer: 140 divided by 9 gives the number of vans needed to carry the tourists
Explanation:

Total number of tourists = 140
Number of students who fit in each van = 9
Number of vans = Quotient of 150 ÷ 9 = 15
The leftover of tourists = Remainder =5
Can be placed in a different van or can be adjusted in the 15 vans.
Question 7.
Part B
What does the remainder mean in the context of the problem?
Type below:
____________
Answer: The leftover of tourists = Remainder =5
Explanation:
The leftover of tourists= Remainder =5
Can be placed in a different van or can be adjusted in the 15 vans.
Question 7.
Part C
How can you use your answer to determine if the tour guide rented enough vans? Explain.
Type below:
____________
Answer: The number of vans would be correct if they were 16 instead of 15
Explanation:
Then the answer can be determined as all the 140 tourists have enjoyed their trip to the fullest and traveled comfortably without any hassle and bustle.
Question 8.
Solve.
3,200 ÷ 8 = ______
Answer: 400
Explanation:

Therefore we can say that the quotient is 400 while the remainder is 0
Page No. 273
Question 9.
Which quotients are equal to 300? Mark all that apply.
Options:
a. 1,200 ÷ 4
b. 180 ÷ 9
c. 2,400 ÷ 8
d. 2,100 ÷ 7
e. 90 ÷ 3
f. 3,000 ÷ 3
Answer: a. 1,200 ÷ 4, c. 2,400 ÷ 8, d. 2,100 ÷ 7
Explanation:
1,200 ÷ 4

Therefore the quotient is 300 and the remainder is 0.
2,400 ÷ 8

Therefore the quotient is 300 and the remainder is 0.
2,100 ÷ 7

Therefore the quotient is 300 and the remainder is 0.
Question 10.
Margo estimated 188 ÷ 5 to be between 30 and 40. Which basic facts did she use to help her estimate? Mark all that apply.
Options:
a. 10 ÷ 5
b. 15 ÷ 5
c. 20 ÷ 5
d. 25 ÷ 5
Answer: b. 15 ÷ 5 c. 20 ÷ 5
Explanation:
188 ÷ 5
STEP 1 Identify the basic fact. 15 ÷ 5
STEP 2 Use place value. 150 = 15 tens
STEP 3 Divide. 15 tens ÷ 5 = 3 tens
150 ÷ 3 = 30
STEP 1 Identify the basic fact. 20 ÷ 5
STEP 2 Use place value. 200 = 20 tens
STEP 3 Divide. 20 tens ÷ 5 = 4 tens
200 ÷ 5 = 40
Therefore we can say that the quotient is between 30 to 40
Question 11.
Mathias and his brother divided 2,029 marbles equally. About how many marbles did each of them receive?
About _________
Answer: about 1,014 marbles each one recieved
Explanation:
Total number of marbles = 2,029
Number of people = 2
Number of marbles each one received = 2,029 ÷ 2 = 1,014
For 12a–12d, choose Yes or No to show how to use the Distributive Property to break apart the dividend to find the quotient 132 ÷ 6.
Question 12.
a. (115 ÷ 6) + (17 ÷ 6)
i. yes
ii. no
Answer: ii. no
Explanation:
According to the question, the nearest estimates are 115 and 17 but these are not divisible by 6.
Question 12.
b. (100 ÷ 6) + (32 ÷ 6)
i. yes
ii. no
Answer: ii. no
Explanation:
According to the question, the nearest estimates are 100 and 32 but these are not divisible by 6.
Question 12.
c. (90 ÷ 6) + (42 ÷ 6)
i. yes
ii. no
Answer: i. yes
Explanation:
STEP1 Find the nearest estimates of the number 132
STEP2 We can break the number 132 into 90 + 42
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (90 ÷ 6) + (42 ÷ 6)
STEP5 Add quotients of the above 15 +7= 22
Question 12
d. (72 ÷ 6) + (60 ÷ 6)
i. yes
ii. no
Answer: i. yes
Explanation:
STEP1 Find the nearest estimates of the number 132
STEP2 We can break the number 132 into 72 + 60
STEP3 We must divide the two parts of the number (dividend) with the divisor.
STEP4 (72 ÷ 6) + (60 ÷ 6)
STEP5 Add quotients of the above 12 +10= 22
Question 13.
There are 60 people waiting for a river raft ride. Each raft holds 15 people. Silvia used the work below to find the number of rafts needed. Explain how Silvia’s work can be used to find the number of rafts needed.
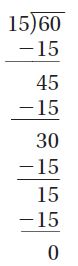
Type below:
_________
Answer: 4
Explanation:
Total number of people = 60
Number of people each river raft can hold = 15
Number of rafts needed to give a ride to all the people = 60 ÷ 15 = 4
Page No. 274
A travelling circus brings along everything it needs for a show in big trucks.
Question 14.
Part A
The circus sets up chairs in rows with 9 seats in each row. How many rows will need to be set up if 513 people are expected to attend the show?
______ rows
Answer: 57
Explanation:
The total number of people = 513
Number of seats in each row = 9
Number of rows = 513 ÷ 9 = 57
Question 14.
Part B
Can the rows be divided into a number of equal sections? Explain how you found your answer.
Type below:
_________
Answer: Yes, the rows can be divided into equal sections. 57 ÷ 3 = 19
Explanation:
We can divide 57 using the divisor as 3, then the quotient is 19 and the remainder is 0.
Question 14.
Part C
Circus horses eat about 250 pounds of horse food per week. About how many pounds of food does a circus horse eat each day? Explain.
About ______ pounds
Answer: About 35 pounds
Explanation:
Mass of food the horses ate in one week = 250 pounds
Number of days in a week =7
Mass of food the horses ate per day = Quotient of 250 ÷ 7 = about 35

Question 15.
Hilda wants to save 825 digital photographs in an online album. Each folder of the album can save 6 photographs. She uses division to find out how may full folders she will have. In what place is the first digit of the quotient?
_________
Answer: Hundreds place
Explanation:
Use place value to place the first digit. Look at the hundreds in 825. 800 hundred can be shared among 6 groups
without regrouping.
Now there is 80 tens and 25 ones to share among 6 groups.
The first digit of the quotient will be in the hundreds place.
Page No. 275
Question 16.
Which model matches each expression? Write the letter in the box next to the model.

Answer: 1st picture – 150 ÷ 30
2nd picture – 160 ÷ 40
3rd picture – 150 ÷ 50
4th picture – 160 ÷ 80
Explanation:
150 ÷ 30

160 ÷ 40

150 ÷ 50

160 ÷ 80

Question 17.
Popcorn was donated for the school fair by 3 different popcorn vendors. They donated a total of 636 bags of popcorn. Each vendor donated the same number of bags. How many bags of popcorn did each vendor donate?
______ bags
Question 18.
Use partial quotients. Fill in the blanks.

Answer: 212
Explanation:
Total number of popcorn bags = 636
Number of popcorn vendors = 3
Number of popcorn bags donated by each vendor = 636 ÷ 3 = 212

Therefore the number of bags donated by each vendor = 212
Page No. 276
Question 19.
Zack needs to divide these base-ten blocks into 3 equal groups.

Draw or describe a model to show how many are in each group.
Type below:
________
Answer: 16
Explanation:
Total number of counters = 48
Number of groups they are supposed to be divided = 3
Then, 48 ÷ 3


Therefore the quotient is 16 and the remainder is 0.
Question 20.
Jim needs to divide 750 coupon books equally among 9 stores. In which place is the first digit of the quotient? Choose the word that makes the sentence true.
The first digit of the quotient is in the  place.
place.
________
Answer: tens place
Explanation:
Use place value to place the first digit. Look at the hundreds in 750. 720 hundred can be shared among 9 groups
without regrouping.
Now there is 72 tens and 30 ones to share among 9 groups.
The first digit of the quotient will be in the tens place.
Question 21.
Ursula bought 9 dozen rolls of first aid tape for the health office. The rolls were divided equally into 4 boxes. How many rolls are in each box?
_____ rolls
Answer: 27 rolls
Explanation:
Number of rolls = 9 dozen x 12 = 108
Number of boxes = 4
Number of rolls in each box = Quotient of 108 ÷ 4 = 27 rolls
Question 22.
There are 112 seats in the school auditorium. There are 7 seats in each row. There are 70 people seated, filling up full rows of seats. How many rows are empty?
_____ empty rows
Answer: 6 rows are empty
Explanation:
Total number of seats = 112
Number of seats in each row = 7
Number of rows = 112÷7 = 16
Number of people seated = 70
Number of rows fully occupied by the people = 70 ÷ 7 = 10
Number of empty rows = 16 – 10 = 6
Page No. 280
Question 1.
Use the arrays to name the factors of 12.
a. ![]()
_____ × _____ = 12
Answer: 6 x 2 = 12
Explanation:
There are a total of 12 counters in the given figure.
So, we can see that 6 + 6 = 12 from the above figure.
Hence we can write as 6 x 2 = 12
Question 1.
b. 
_____ × _____ = 12
Question 1.
Answer: 4 x 3 = 12
Explanation:
The number of columns and rows are 4 and 3 respectively.
So we can calculate the multiplication by 4 x 3 = 12
c. ![]()
_____ × _____ = 12
Answer: 6 x 2 = 12
Explanation:
The number of columns and rows are 4 and 3 respectively.
So we can calculate the multiplication by 4 x 3 = 12.
Use tiles to find all the factors of the product. Record the arrays and write the factors shown.
Question 2.
5: __________
Type below:
________
Answer:
Explanation:
Question 3.
20: __________
Type below:
________
Answer:
Explanation:
Question 4.
25: __________
Type below:
________
Answer:
Explanation:
Page No. 281
Practice: Copy and Solve Use tiles to find all the factors of the product. Record the arrays on grid paper and write the factors shown.
Question 5.
9: ______________
Type below:
________
Answer:
Explanation:
Question 6.
21: ______________
Type below:
________
Answer:
Explanation:
Question 7.
17: ______________
Type below:
________
Answer:
Explanation:
Question 8.
18: ______________
Type below:
________
Answer:
Explanation:
Use the diagram for 9–10.

Question 9.
Pablo is using 36 tiles to make a patio. Can he arrange the tiles in another way and show the same factors? Draw a quick picture and explain.
Type below:
________
Answer:
Explanation:
Question 10.
How many different rectangular arrays can Pablo make with all 36 tiles, so none of the arrays show the same factors?
________ rectangular arrays
Answer:
Explanation:
Question 11.
If 6 is a factor of a number, what other numbers must be factors of the number?
Type below:
________
Answer:
Explanation:
Question 12.
Jean spent $16 on new T-shirts. If each shirt cost the same whole-dollar amount, how many could she have bought?
Type below:
________
Answer:
Explanation:
Page No. 282
Question 13.
Carmen has 18 connecting cubes. She wants to model a house shaped like a rectangle. If the model has a height of one connecting cube, how many different ways can Carmen model the house using all 18 connecting cubes?

a. What do you need to know?
Type below:
________
Answer:
Explanation:
Question 13.
b. How is finding the number of ways to model a rectangular house related to finding factor pairs?
Type below:
________
Answer:
Explanation:
Question 13.
c. Why is finding the factor pairs only the first step in solving the problem?
Type below:
________
Answer:
Explanation:
Question 13.
d. Show the steps you used to solve the problem.
Type below:
________
Answer:
Explanation:
Question 13.
Complete the sentences. Factor pairs for 18 are ___________________ .
There are ______ different ways Carmen can arrange the cubes to model the house.
Type below:
________
Answer:
Explanation:
Question 14.
Sarah was organizing vocabulary words using index cards. She arranged 40 index cards in the shape of a rectangle on a poster. For 14a–14e, choose Yes or No to tell whether a possible arrangement of cards is shown.
a. 4 rows of 10 cards
i. yes
ii. no
Answer:
Explanation:
Question 14.
b. 6 rows of 8 cards
i. yes
ii. no
Answer:
Explanation:
Question 14.
c. 20 rows of 2 cards
i. yes
ii. no
Answer:
Explanation:
Question 14.
d. 40 rows of 1 card
i. yes
ii. no
Answer:
Explanation:
Question 14.
e. 35 rows of 5 cards
i. yes
ii. no
Answer:
Explanation:
Conclusion:
I think the answers provided in the Go Math Grade 4 Answer Key Chapter 4 Divide by 1-Digit Numbers are beneficial for all the students of 4th grade. Our aim is to help the students to become masters in maths. So, Refer to our HMH Go Math 4th Grade Answer Key Chapter 4 Divide by 1-Digit Numbers and secure good marks in the exams.
