Go Math Grade 3 Answer Key Chapter 9 Compare Fractions Assessment Test

Enhance your skills using the Go Math Grade 3 Answer Key Chapter 9 Compare Fractions Assessment Test. Score better grades in the exam by practicing using the 3rd Grade Go Math Answer Key Ch 9 Compare Fractions Assessment Test. We have listed all the topics of Chapter 9 in our Assessment Test and even provided Solutions to all the problems given.

Students can check how much they understood the topics by solving the Questions in Grade 3 Go Math Chapter 9 Compare Fractions Assessment Test. Get acquainted with the areas you are lagging and improvise on them accordingly.

Chapter 9: Compare Fractions Assessment Test

• Test – Page 1 – Page No. 91
• Test – Page 2 – Page No. 92
• Test – Page 3 – Page No. 93
• Test – Page 4 – Page No. 94
• Test – Page 5 – Page No. 95
• Test – Page 6 – Page No. 96

Test – Page 1 – Page No. 91

Question 1.
Frank and Dwayne weed their gardens that are the same size. Frank’s garden is divided into 6 equal sections. Dwayne’s garden is divided into 4 equal sections. Each boy has weeded 2 sections of his garden.
Write a fraction to describe what part of his garden each boy has weeded. Then tell who weeded a larger area. Explain
_________

Answer: Dwayne’s part 2/4 > Frank’s part 2/6.

Explanation:
Frank and Dwayne has the same size of gardens
Frank’s garden is divided into 6 equal sections
Dwayne’s garden is divided into 4 equal sections
Since each has weeded 2 sections of their gardens, Frank’s part would be = 2/6,
Dwayne’s part would be = 2/4.
Therefore Dwayne’s part 2/4 > Frank’s part 2/6,
Since the garden with a greater number of sections will have a smaller area per section.

Question 2.
Eli, Beth, and Cory are reading the same book for class. Eli read \(\frac{3}{4}\) of his book. Beth read \(\frac{3}{8}\) of her book and Cory read \(\frac{3}{6}\) of his book. For 2a–2d, choose Yes or No to indicate whether the comparisons are correct.
a. \(\frac{3}{4}\) > \(\frac{3}{8}\)
i. yes
ii. no

Answer: Yes.

Explanation: 3/4 > 3/8. Since both are reading the same book and book with a greater number of sections will have a lesser value.

Question 2.
b. \(\frac{3}{6}\) < \(\frac{3}{8}\)
i. yes
ii. no

Answer: No, 3/6 < 3/8.

Explanation: It’s not true, Since both are reading the same book, and books with a greater number of sections will have a lesser value. Therefore 3/6 > 3/8).

Question 2.
c. \(\frac{3}{8}\) = \(\frac{3}{6}\)
i. yes
ii. no

Answer: No

Explanation: 3/8 = 3/6. Both are not equal, since the same book has been divided into different no of parts. Therefore both are not equal.

Question 2.
d. \(\frac{3}{6}\) < \(\frac{3}{4}\)
i. yes
ii. no

Answer: Yes.

Explanation: 3/6 < 3/4. Since both are reading the same book and book with a greater number of sections will have a lesser value.

Question 3.
Mark and Lisa are on the swim team. Mark swims \(\frac{3}{8}\) mile each day. Lisa swims \(\frac{5}{8}\) mile each day. Which statement is correct? Mark all that apply.
Options:
a. Mark swims farther than Lisa each day.
b. Lisa swims the same distance as Mark each day.
c. Lisa swims less than 1 mile each day.
d. Lisa swims farther than Mark each day.

Answer: Both c and d are correct.

Explanation: Lisa swims less than 1 mile while 5/8 mile each day and She swims farther than Mark each day. i.e. 5/8 > 3/8.

Test – Page 2 – Page No. 92

Question 4.
MacKenzie and Cassie used fabric to make costumes for a play. MacKenzie used \(\frac{3}{4}\) yard of fabric and Cassie used \(\frac{5}{6}\) yard. Who used more fabric? Explain the strategy you used to solve the problem.
_________

Answer:
MacKenzie divided fabric into 4 equal parts and used 3/4 of it. So, 1/4 of it is left. Cassie divided the same yard of fabric into 6 equal parts and used 5/6 of it. Here 1/6 part of it is left, by comparing leftover pieces we can conclude 1/4 > 1/6. Since the larger piece was left with MacKenzie, Cassie has used more fabric.

Question 5.
The soccer team practices passing for \(\frac{3}{4}\) hour and shooting for \(\frac{4}{5}\) hour. On which drill does the team spend less time? Explain how you can use the model to find the answer.

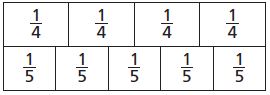
Answer: From the model, we can understand that team has spent less time on Passing. Since the model for 3/4 is shorter than the model for 4/5.

Question 6.
Andrew bought \(\frac{7}{8}\) pound of mixed nuts. Margaret bought \(\frac{5}{8}\) pound of mixed nuts. Use the fractions and symbols to show which amount is greater.

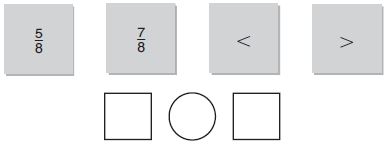
Answer: 5/8 < 7/8 or 7/8 > 5/8

Explanation:

Test – Page 3 – Page No. 93

Question 7.
Mr. Worth opened new jars of 4 different colors of paint for an art project. All of the jars were the same size.

Part A Draw lines to show how Mr. Worth could divide one jar of paint into halves, one into thirds, one into fourths, and one into sixths.
Part B Students in his class used an equivalent amount of two paint colors. Use the models to show the amount of paints used. Write two pairs of equivalent fractions to represent the models.

Answer: The below figure represents halves, one-third, one into fourth, one into sixths.

Explanation:

Representing Halves           one-third                      one into fourth           one into sixths
Therefore from the above figure, two pairs of equivalent fractions representing the models are 1/2 = 2/4, 1/3 = 2/6.

Question 8.
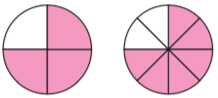
Dalton rode his skateboard for \(\frac{3}{4}\) mile. Amelia rode her skateboard for an equal distance. What is an equivalent fraction that describes how far Amelia rode? Use the models to show your work.

\(\frac{3}{4}\) = \(\frac{□}{□}\)

Answer: \(\frac{3}{4}\) = \(\frac{6}{8}\).

Explanation: Below two pictures give Dalton and Amelia distance covered while riding a skateboard. Though they both rode the same distance to represent them in similar different fractions. We can divide Dalton’s covered as in the 1^st circle and Amelia’s in 2^nd Circle. From the pictures, equivalent fractions will be 3/4 for Dalton and 6/8 for Amelia.

Question 9.
Mr. Barrows opens 2 packs of paper. He puts \(\frac{2}{5}\) of a pack in one pile and \(\frac{3}{5}\) of a pack in another pile. Which pile has more paper? Show your work.
\(\frac{□}{□}\) of a pack

Answer: 3/5 of a pack has more papers.

Explanation: The pile with 3/5 of a pack has more papers. Since 2/5 is there in another pack.

Test – Page 4 – Page No. 94

Question 10.
Treyvon watched \(\frac{2}{8}\) a movie. Juan watched \(\frac{2}{6}\) of the same movie. Use >, =, or < to compare the parts that they watched.
\(\frac{2}{8}\) _____ \(\frac{2}{6}\)

Answer: \(\frac{2}{8}\) < \(\frac{2}{6}\) or \(\frac{2}{6}\) > \(\frac{2}{8}\).

Question 11.
Alison used \(\frac{7}{8}\) quart of orange juice and \(\frac{3}{8}\) quart of cranberry juice to make some punch.
For 11a–11d, select True or False for each comparison.
a. \(\frac{7}{8}\) < \(\frac{3}{8}\)
i. True
ii. False

Answer: False.

Explanation: 7/8 is greater than 3/8.

Question 11.
b. \(\frac{7}{8}\) > \(\frac{3}{8}\)
i. True
ii. False

Answer: True.

Explanation: Since both have the same denominators, we can compare their numerators directly. Here 7 is greater than 3, therefore 7/8 is greater than 3/8.

Question 11.
c. \(\frac{3}{8}\) < \(\frac{7}{8}\)
i. True
ii. False

Answer: True.

Explanation: \(\frac{3}{8}\) < \(\frac{7}{8}\)

Question 11.
d. \(\frac{3}{8}\) = \(\frac{7}{8}\)
i. True
ii. False

Answer: False.

Explanation: Both are not equal.

Question 12.
Will, Ann, and Jim are working on their science fair projects. Will has finished \(\frac{1}{4}\) of his project. Ann has finished \(\frac{3}{4}\) of her project, and Jim has finished \(\frac{2}{3}\) of his project.
Part A
Who has finished less of their project, Will or Ann?
Explain how you know.
__________

Answer: Will has finished less compared to Ann.

Explanation: Given that will has finished 1/4 of his project wherein Ann has finished 3/4 of her project. Since 1/4 and 3/4 have the same denominator, so we can compare the numerator directly. Since 1 is less than 3, we can say 1/4 is less than 3/4. Thus Will has finished less part of his project compared to Ann.

Question 12.
Part B
Who has finished less of their project, Ann or Jim?
Explain how you know.
__________

Answer: 2/3 is less than 3/4. Therefore, Jim has finished less part of his project compared to Ann.

Explanation: Given that Jim has finished 2/3 of his project were in Ann has finished 3/4 of her project. Since denominators are not the same to compare first we shall make the same. Therefore multiply Jim’s work (2/3) with (4/4) which gives = 8/12 and Ann’s work (3/4) with (3/3) which gives = 9/12. Now by comparing numerators 8/12 is less than 9/12, which means Jim has finished less part of his project compared to Ann.

Test – Page 5 – Page No. 95

Question 13.
Sarah needs \(\frac{4}{6}\) yard of ribbon to wrap a gift. She has 6 pieces of ribbon with the following lengths. She can cut the piece if it is too long. Mark all of the pieces of ribbon that Sarah could use.
Options:
a. \(\frac{1}{2}\) yard
b. \(\frac{6}{6}\) yard
c. \(\frac{3}{8}\) yard
d. \(\frac{4}{4}\) yard
e. \(\frac{1}{3}\) yard
f. \(\frac{5}{6}\) yard

Answer: Sarah could use 6/6 yard, 4/4 yard and 5/6 yard of ribbons to wrap gift.

Explanation:
Given that Sarah needs a 4/6 yard of ribbon to wrap a gift.
Lengths of available ribbons are 1/2, 6/6, 3/8, 4/4,1/3, and 5/6.
Comparing all the lengths with 4/6 – 6/6 and 5/6 are having the same denominators. So we compare only their numerators, both 6 and 5 are greater than 4. So these two ribbons are more than enough for her gift wrapping. With ribbon length, 4/4 yard – since complete ribbons all the parts of the ribbon are available thus this length also enough to wrap the gift. Remaining 1/2, 3/8, and 1/3 – we shall make their denominators equal to 4/6 to compare
multiply (1/2) with (3/3) = 3/6, 3 is less than 4 in 4/6. So this is not having enough length
multiply (1/3) with (2/2) = 2/6, 2 is also less than 4. So this also not having enough length.
multiply (3/8) with (6/6) = 18/48 and (4/6) with (8/8) = 32/48. Since 18 is less than 32, this ribbon length also won’t be enough to wrap gifts. Thus Sarah could use only 6/6 yard, 4/4 yard, and 5/6 yard of ribbons to wrap the gift.

Question 14.
There are 8 people having breakfast. Each person wants \(\frac{1}{2}\) of an omelet. How many whole omelets are needed? Use the models to show your answer.

_____ omelets

Answer: Total they need 4 omelets.

Explanation:
Total no of having omelets are = 8
Each person need 1/2 of omelette, so for 8 persons = (1/2) * 8 = 4.

Question 15.
Michele mixed \(\frac{3}{4}\) cup of flour with \(\frac{1}{2}\) cup of water to make paste for an art project. Compare the fractions. Choose the symbol that makes the statement true.

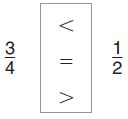
\(\frac{3}{4}\) _____ \(\frac{1}{2}\)

Answer: \(\frac{3}{4}\) > \(\frac{1}{2}\).

Explanation:

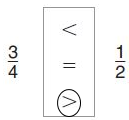
Let’s make 3/4 and 1/2 denominators the same (1/2) * (2/2) = 2/4.
Since 3 is greater than 2, 3/4 > 1/2.

Question 16.
Jeff has three boxes that weigh \(\frac{5}{8}\), \(\frac{1}{8}\), and \(\frac{3}{8}\) pound. Write the weights in order from least to greatest.

Answer: \(\frac{1}{8}\), \(\frac{3}{8}\), \(\frac{5}{8}\).

Explanation: Weights in the least to greatest form 1/8, 3/8, 5/8.

Test – Page 6 – Page No. 96

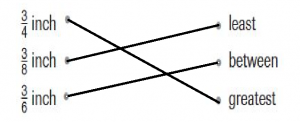
Question 17.
Ben measures the lengths of three insects. Draw a line to match each length on the left to the word on the right that describes its place in the order of lengths.

Answer:

Question 18.
Kerri drew a model to show equivalent fractions.

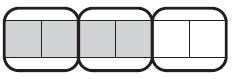
Use the model to complete the number sentence.
\(\frac{2}{3}\) = \(\frac{□}{□}\)

Answer: \(\frac{2}{3}\) = \(\frac{4}{6}\).

Explanation: Here from the model four parts are shaded out of 6, which also equal to \(\frac{2}{3}\) by value.

Question 19.
Elaine brought \(\frac{3}{4}\) pound of potato salad to a picnic. Jake brought \(\frac{2}{3}\) pound of macaroni salad. Who brought more salad? Explain the strategy you used to solve the problem.

Answer: Elaine has brought more Salad compared to Jake.

Explanation:
Elaine has brought \(\frac{3}{4}\) pound of potato salad
Jake brought \(\frac{2}{3}\) pound of macaroni salad
Lets compare both parts by making their denominators same.Therefore multiply (3/4) * (3/3) = (9/12) and (2/3) * (4/4) = (8/12)
Since 8 is less than 9,\(\frac{8}{12}\)  < \(\frac{9}{12}\).
Which means \(\frac{2}{3}\) < \(\frac{3}{4}\). Thus Elaine has brought more Salad compared to Jake.

Question 20.
It took Mike \(\frac{2}{6}\) hour to clean his room.

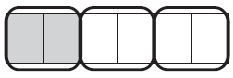
What fraction is equivalent to \(\frac{2}{6}\) ?
\(\frac{2}{6}\) = \(\frac{□}{□}\)

Answer: \(\frac{2}{6}\) = \(\frac{1}{3}\).

Final Words

Hope the knowledge shared regarding the Go Math Grade 3 Answer Key Chapter 9 Compare Fractions Assessment Test. To know more such info feel free to reach us via comment box and we will get back to you. Check out Go Math Grade 3 Answer Key Chapter 9 Compare Fractions to know more related topics.