Know the definition of a circle, the general form of the equation of a circle. Get the various terms involved in the general and standard form of a circle, formulae, and definition, etc. Refer to solved examples of a circle, standard equation of a circle. For your reference, we have included the solved examples on how to find the general form of an equation of the circle, conversion from standard form to general form and vice versa, etc.
Also, Read: Circumference and Area of Circle
Circle Definition
The circle is defined as the locus of a point that moves in a plane such that its distance from a fixed point in that plane is always constant. The center of the circle is the fixed point. The set of points in the plane at a fixed distance is called the radius of the circle.
General Form of the Equation of a Circle
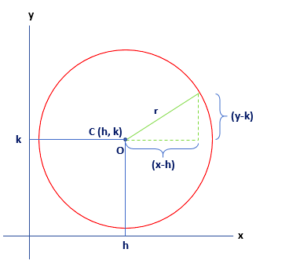
To find the general form of the equation of a circle, we use the below-given graph. Each circle form has its own advantages. Here, we can take an example of a standard form which is great for determining the radius and center just with a glance at the above equation. The general form of a circle is good at substituting ordered pairs and testing them. We use both of these forms. So this gives us an idea that we should interchange between these forms. Firstly, we will transform the standard form to the general form.
General form of equation is (x-h)2 + (y-k)2 = r2
where r is defined as the radius of the circle
h, k is defined as the center coordinates
Standard Form to General Form
Here, we will take an example that gives us an idea to transform an equation from a Standard form to a general form
Eg: Transform (x – 3)2 + (y + 5)2 = 64 to general form.
(x – 3)2 + (y + 5)2 = 64
Now, all the binomial should be multiplied and rearranged till we get the general form.
(x – 3) (x – 3) + (y + 5) (y + 5) = 64
(x2 – 3x – 3x + 9) + (y2 + 5y + 5y + 25) = 64
x2 – 6x + 9 + y2 + 10y + 25 = 64
x2 + y2 – 6x + 10y + 9 + 25 – 64 = 0
(x2) + (y2) – 6(x) + 10(y) – 30 = 0
x2+y2–6x+10y–30 = 0
This is the general form of the equation as transformed from Standard from.
General to Standard Form
To transform an equation to standard form from a general form, we must first complete the equation balanced and complete the square. Here, completing the square implies creating Perfect Square Trinomials(PST’s).
To give you an idea about Perfect Square Trinomials, here are some examples
Example 1:
x2 + 2x + 1
When we factor PSTs, we get two identical binomial factors.
x2 + 2x + 1 = (x + 1)(x + 1) = (x + 1)2
Example 2:
x2 – 4x + 4
When we factor PSTs, we get two identical binomial factors.
x2 – 4x + 4= (x – 2)(x – 2) = (x – 2)2
We can observe that the sign for the middle term can either be positive or negative.
We have a relationship between the last term and the coefficient of the middle term
(b/2)2
Now, we see a few examples of circle equation that include the transformation of the equation from a standard form to the general form
General Form of the Equation of a Circle Examples
Problem 1:
The circle equation is: x2 + y2 – 8x + 4y + 11 = 0. Find the centre and radius?
Solution:
To find the centre and radius of the circle, we first need to transform the equation from general form to standard form
x2 + y2 – 8x + 4y + 11 = 0
x2 – 8x + y2 + 4y + 11 = 0
(x2 – 8x + ) + (y2 + 4y + ) = -11
We are leaving the spaces empty for PST’s.
We must complete the square of the PST’ds by adding appropriate values
To maintain balance on the above equation, we must add same values on the right side which we add on the left side of the equation to keep the equation equal on both the sides
(x2 – 8x + 16) + (y2 + 4y + 4) = -11 + 16 + 4
(x – 4)2 + (y + 2)2 = 9
By comparing the above equation with the standard form of the circle, we observe that
Centre =(4,-2)
Radius = 3
Problem 2:
Find the standard form of the equation of a circle of radius 4 whose centre is (-3,2). Convert the equation into general form
Solution:
As given in the question,
radius = 4
h = -3
k = 2
General form of equation is (x-h)2 + (y-k)2 = r2
(x-(-3))2 + (y-2)2 = 42
(x+3)2 + (y-2)2 = 16
x2 + 6x + 9 + y2 -4y + 4 = 16
x2 + y2 + 6x – 4y – 3 = 0
Therefore, the general solution is x2 + y2 + 6x – 4y – 3 = 0
Problem 3:
Write the equation in the general form given the radius and centre
r = 3, centre = (1,2)
Solution:
As given in the question,
r = 3
h = 1
k = 2
General form of equation is (x-h)2 + (y-k)2 = r2
(x-1)2 + (y-2)2 = 32
x2 – 2x + 1 + y2 -4y + 4 = 9
x2 + y2 – 2x – 4y – 4 = 0
Therefore, the general solution is x2 + y2 – 2x – 4y – 4 = 0