Know the fundamental concepts of Geometry here. We are providing detailed information regarding point, plane, ray, line segment, incidence properties of lines in a plane, collinear points, concurrent lines, two lines in a plane, etc. Follow the important points and basics of geometry. Go through the below sections to know the formulas, examples of all the basic geometry concepts.
Fundamental Concepts of Geometry – Introduction
The term “Geometry” is derived from the Greek word “Geometron” where Geo means “Earth” and Metron means “Measurement”. Geometrical ideas are basically reflected in various forms of engineering, architecture, art, measurements, etc. Different objects have different shapes where the ball is round in shape and the ruler is straight. Know some of the interesting facts that enable us to learn more about shapes around us.
Geometry is basically divided into two types such as solid geometry and plane geometry. There are certain formulae for measuring all the geometric concepts. The basic geometric concepts are as follows:
Point
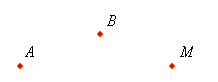
Point is considered as the fundamental object in euclidean geometry. It determines the location which has no length, breadth, and thickness. The small dot marked by pencil or pen on a paper or sheet made by a fine needle is few examples of a point. It is represented with (.). Every point has to be denoted with a name and we have to use a single capital letter for it. Representation of points of A, B and M are as follow:
Lines
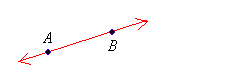
The basic concept of a line is its straightness which can indefinitely extend in both ways or directions. The 2 arrowheads placed in opposite directions indicate that the line length is unlimited. The line has only length but not thickness or breadth which has no endpoints. Lines are made up of an infinite number of points. Lines also must have names as the points do, therefore we can refer to them easily. Lines are represented with (↔). If a line is passing through the points A and B, then it is denoted with line notation of AB ↔ and graphically represented as:
Plane
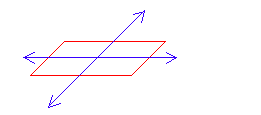
Planes are nothing but flat surfaces. The plane has length and breadth but not thickness. The basic concept of the plane is its flatness and it extends in all directions indefinitely. The length and breadth of the plane are always unlimited and are two-dimensional. The plane is made up of an infinite amount of lines and two-dimensional figures are called plane figures. All the lines and points which lie on the same plane are known as coplanar. Plane in graphical representation is represented as:
Line Segment
The line segment is the portion of a line between the points. Two or more line segments are said to be equal if and only if they have the same length. If two lines are parallel, then their line segments are said to be in parallel. If the length of the line is infinite, we use a part of the line where the line segment connects both the endpoints. The line segment with both endpoints A and B are denoted with the line segment notation AB —.
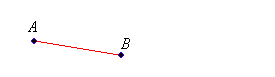
The line segment will be drawn as part of the line.
Ray
The line of unlimited length and one end is called the ray. The unlimited number of rays can be drawn with the initial point. If there are two rays with similar initial point and extending in opposite direction are called as opposite rays. Two rays are said to be in parallel if and only if the lines between them are parallel. The ray that is starting from A and passing through B is denoted by AB→
Angles
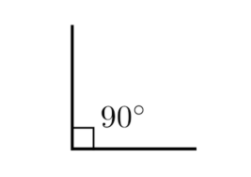
The angle is a combination of both rays with the common endpoint. The angle is represented with the symbol “⌊”. The point of the corner at an angle is called the vertex. The angle contains two straight sides which are called the arms of the angle.
How to Measure Angles?
The angle consists of 2 rays with the common endpoint. Both rays are known as the sides of the angle and the common endpoint is the angle vertex. For each angle that is rotated about the vertex will have a measure which is determined by terminal side rotation about the initial side. If it is rotated counterclockwise, it generates the positive angle measure and a clockwise rotation generates the negative angle measure.
Angles are measured in units called radians or degrees. Angles are classified into various types based on the measure: right angle, obtuse angle, acute angle, straight angle
There are specific conditions for the angles like
- If two positive angles measure a sum of 90°, then the angles are called complementary angles
- If two positive angles measure a sum of 180°, then the angles are called supplementary angles
Difference between Line Segment, Line and Ray
| Line Segment | Ray | Line |
|---|---|---|
| Line Segment is the part of the line with two fixed points | Ray is the part of the line with one infinite end and one fixed starting point | The line can be drawn on a plane with o fixed endpoints |
| Line Segment can be drawn on the piece of the paper | Ray cannot be drawn on the paper and can be represented in the diagram only | The line cannot be drawn on the paper and can be represented in the diagram only |
| The length of the line segment is definite so it can be measured | The length of the ray cannot be measured as one of its ends is indefinite | The length of the line cannot be measured as one of its lengths is indefinite |
| Line Segment can be represented with AB— | Ray can be represented with AB→ | The line can be represented with AB↔ |
| Symbol of Line Segment is ⋅—⋅ with 2 dots which are at the either ends to indicate that they are fixed | The symbol of Ray is ⋅—> with 1 dot at the starting and an arrowhead to indicate it and goes in the other direction | Symbol of Line is <—> with two arrow marks at either ends to indicate they go in both directions |
Collinear Points
Two or more points that lie on the same line in the plane are known as collinear points.
- Here the line is known as the line of colinearity.
- Both the points are always collinear.

In the above diagram,
Points A, B, and C are the points collinear lying on a line.

X, Y, and Z are not collinear points because those three points do not lie on the same line. Therefore, they are non-collinear points.

In the above diagram M, N, O, P, Q are collinear points and A, B are non-collinear points.
Quick Links
| Nets of Solids | Triangle | Types of Lines |
| Some Geometric Terms and Results | Geometric Design and Models | Points, Lines, and Shapes |
Incidence Properties of a Line in a Plane
If a point is given in a plane, then an infinite number of lines can be drawn to pass through it. With the given point in the plane, infinitely many lines can be drawn to pass through it.
Two clear points in the plane will determine the unique line. Only one line can be drawn to pass through the given points and the line lies in the plane completely.
![]()
An infinite number of points will lie on a similar plane.
![]()
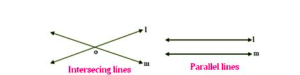
Two lines in the plane will either intersect or are parallel to each other.
Concurrent Lines
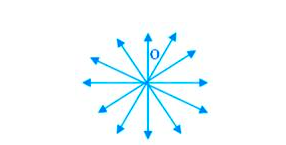
Three or more lines that pass through the same point are known as concurrent lines and the common point of the line is called the point of concurrency.
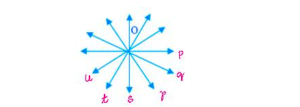
In the above figure p, q, r, s, t, u meet and intersect at the point O which are called concurrent lines.
Geometric Theorems
The Triangle Angle Sum Theorem
All the interior angles of a triangle will have the sum of 180°
The (OAT) Opposite Angle Theorem
The opposite angles are equal, if two straight lines cross
Parallel Lines Theorem
If the parallel lines are cut by the transversal
a) alternate angles will be equal (PLT – Z)
b) corresponding angles will be equal (PLT – F)
c) interior angles will have the sum of 180° (PLT – C)
