In general, we use Subtraction to obtain the difference, find missing parts, or compare numbers. By the end of this article, you will get acquainted with the details such as the relationship between addition and subtraction facts, solve questions when addition and subtraction operations are given together, etc. You can find the difference when a number is subtracted from the other number, when zero is subtracted from a number. Check out solved examples on finding the difference using properties of subtraction.
Do Refer:
- Subtraction
- Subtraction Worksheets
- Subtraction Placing the Numbers
- Subtracting Numbers in Expanded Form
How to find the Difference using Subtraction Properties?
- We can subtract only if the number to be subtracted is smaller than the number from which it is to be subtracted, i.e. minuend should always be greater than the subtrahend.
- We can subtract the numbers even in the case of Minuend and Subtrahend being the Same i.e. the difference will be zero.
- On Subtracting Zero from a number, the number remains the same.
- When a Number is Subtracted from itself the difference is zero.
- Subtraction is nothing but the inverse of addition Operation. For every Subtraction Fact, there are two Addition Facts. It is applicable for Addition Operation too i.e. for every Addition Fact, there are two Subtraction Facts.
Examples on Finding the Difference using Subtraction Property
Example 1.
Subtract 30 from 64?
Solution:
Here the Minuend is 64 and Subtrahend is 30.
We can perform the subtraction operation as the minuend is greater than the subtrahend. i.e. 64>30
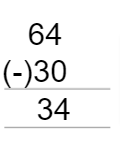
Example 2.
Subtract the first number from the second number in the following
(i)12, 45
(ii)5, 12
(iii)20, 35
Solution:
(i)12, 45
Here the Minuend 45 is greater than 12. On Subtracting them, we will get the difference as under
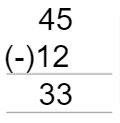
The difference between 45 and 12 is 33.
(ii)5, 12
In this case, the minuend is 12 and the subtrahend is 5. We will get the difference as follows
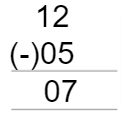
Thus, 12-5 is 07
(iii)20, 35
Here, the minuend is 35 and subtrahend is 20. we will have the difference as below
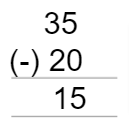
Thus, 35-20 is 15.
Example 3.
(i) 4 + 6 = 10, then 10 – 6 = 4, and 10 – 4 = 6
(ii) 12 + 5 = 17, then 17-5 = 12, 17-12 =5
(iii) 07 + 15 = 22, then 22 – 15 = 07, and 22 – 07 = 15
(iv) 13 + 06= 19, then 19 – 06 = 13, and19 -13 = 06
Example 4.
(i) 18 – 2 = 16, then 16 + 2 = 18, and 2 + 16 =18
(ii) 11 – 6 = 05, then 6 + 05 = 11, and 05+ 6 = 11
(iii) 60 – 40 = 20, then 40 + 20 = 60, and 20 + 40 = 60
(iv) 48 – 20 =28, then 20 + 28 = 48, and 28 + 20 = 48
Example 5.
(i) 12-0 =12
(ii) 24-0 = 24
(iii)48 -0 = 48
(iv)56-0 = 56
If Zero is Subtracted from a number then the number remains the same.
Example 6.
Find the Difference in the following
(i)9-9 = 0
(ii)12-12 = 0
(iii)142-142 = 0
(iv)265-265 = 0
(v)323-323=0
If you subtract the numbers having both the same minuend and subtrahend the difference would be zero.
