When a dividend divides the divisor completely, the quotient and divisor are called the factors of the dividend and the dividend called the multiple. We can also compute the factors of the multiple by using the division facts. Get the simple steps to get the multiples and factors by using the division fact along with the solved examples in the below sections.
Do Read:
Factors and Multiples by using Division Facts
In maths, a factor is a number that is an exact divisor with no remainder. Multiple is nothing but a number obtained when multiplied by other numbers. We use multiplication to find the multiples. Multiplication is the inverse operation of division. When a dividend is divided by a divisor, we get a quotient and the dividend is again divided by the quotient that gives the divisor.
We can use division facts to get the factor and multiples of the expression. The division fact formula is the dividend ÷ divisor = quotient. Here, quotient and divisor are the factors of the multiple dividend.
Examples:
Divide 64 by 4
64 ÷ 4 = 16
Here, 4 and 16 are factors of 64.
Divide 18 by 9
18 ÷ 9 = 2
Here, 9 and 2 are factors of 18.
Also, Check:
How to Find Multiples, Factors Using Division Facts?
Get a detailed explanation on how to find the factors of multiple using the division facts in the below sections.
- Get the multiple by observing the division fact.
- At, first divide the multiple by 1 and get the result.
- Divide the multiple by another number which leaves the remainder zero.
- Continue the process, till you get all the factors.
Examples on Finding Multiples and Factors Using Division Facts
Example 1:
Find the factors of the division fact 180 ÷ 6 = 30.
Solution:
Given division fact is 180 ÷ 6 = 30.
Multiple is 180
Find the factors of 180
180 ÷ 1 = 180
180 ÷ 2 = (18 ÷ 2) x 10 = 9 x 10 = 90
180 ÷ 3 = (18 ÷ 3) x 10 = 6 x 10 = 60
180 ÷ 4 = 45
180 ÷ 5 = 36
180 ÷ 6 = 30
180 ÷ 9 = 20
180 ÷ 10 = 18
180 ÷ 12 = 15
180 ÷ 15 = 12
180 ÷ 18 = 10
180 ÷ 20 = 9
180 ÷ 30 = 6
180 ÷ 36 = 5
180 ÷ 45 = 4
180 ÷ 60 = 3
180 ÷ 90 = 2
180 ÷ 180 = 1
The factors f 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180
Example 2:
Find the factors of 42.
Solution:
Given multiple is 42
Write the factors of 42 using the division fact.
42 ÷ 1 = 42
42 ÷ 2 = 21
42 ÷ 3 = 14
42 ÷ 6 = 7
42 ÷ 7 = 6
42 ÷ 14 = 3
42 ÷ 21 = 2
42 ÷ 42 = 1
So, the factors of multiple 42 are 1, 2, 3, 6, 7, 14, 21, and 42.
Example 3:
Is 500 is a multiple of 11? Use division.
Solution:
Given that,
Dividend = 500
Divisor = 11
Divide 500 by 11
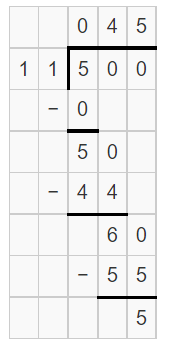
500 ÷ 11 = 45 with a remainder of 5
It leaves a remainder, so 500 is not a multiple of 11.
Example 4:
Is 7 a factor of 21?
Solution:
Given that,
Dividend = 21
divisor = 7
divide 21 by 7
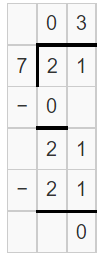
21 divided by 7 doesn’t leave a remainder.
So, 7 is a factor of 21.
FAQs’s on Factors and Multiples by using Division Facts
1. What is the division method?
The division is one of the basic arithmetic operations, which means repeated subtraction. The division method is used to split a group into a number of equal parts. The parts of division are dividend, divisor, remainder and quotient.
2. What is a basic division fact?
Division fact is nothing but a number that should be completely divisible by dividend to get the quotient. In division fact, the remainder is always zero. For any three numbers, it is possible to write exactly two division facts.
3. How do you factor a number by a division method?
Divide the multiple by the smallest possible number that divides the number exactly and repeat the process. The numbers that divide the multiple are called the factors.
