Examples to find the Least Common Multiple of three numbers by using the Division Method are available on this page. We write the given numbers in a row separately by commas, then divide the numbers by a common prime number. The lowest common multiples for two numbers or three numbers are the same. The least common multiples are used to add and subtract the fraction with different denominators. Students who wish to become master in 5th Grade Math are suggested to refer to this article and practice the problems given below.
Do Refer:
- To Find Lowest Common Multiple by using Division Method
- Examples to find Least Common Multiple of two numbers by using Division Method
- To find Least Common Multiple by using Prime Factorization Method
- Examples to find Least Common Multiple by using Prime Factorization Method
LCM of Three Numbers using Division Method Examples with Answers
Example 1.
What is the least common multiple (L.C.M) of 7, 14, and 21 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
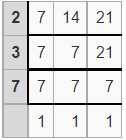
LCM = 2 x 3 x 7
Thus the least common multiple (L.C.M) of 7, 14, and 21 = 42
Therefore, LCM(7, 14, 21) = 42
Example 2.
What is the least common multiple (L.C.M) of 6, 12, and 18 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
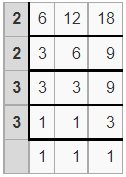
LCM = 2 x 2 x 3 x 3
Thus the least common multiple (L.C.M) of 6, 12 and 18 = 36
Therefore, LCM(6, 12, 18) = 36
Example 3.
What is the least common multiple (L.C.M) of 4, 16, and 24 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
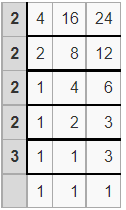
LCM = 2 x 2 x 2 x 2 x 3
Thus the least common multiple (L.C.M) of 4, 16 and 24 = 48
Therefore, LCM(4, 16, 24) = 48
Example 4.
What is the least common multiple (L.C.M) of 18, 48, and 64 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
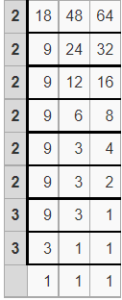
LCM = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3
Thus the least common multiple (L.C.M) of 18, 48 and 64 = 576
Therefore, LCM(18, 48, 64) = 576
Example 5.
What is the least common multiple (L.C.M) of 12, 30, and 40 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
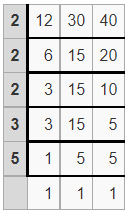
LCM = 2 x 2 x 2 x 3 x 5
Thus the least common multiple (L.C.M) of 12, 30 and 40 = 120
Therefore, LCM(12, 30, 40) = 120
Example 6.
What is the least common multiple (L.C.M) of 3, 6, and 27 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
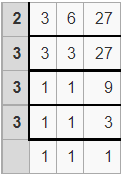
LCM = 2 x 3 x 3 x 3
Thus the least common multiple (L.C.M) of 3, 6 and 27 = 54
Therefore, LCM(3, 6, 27) = 54
Example 7.
What is the least common multiple (L.C.M) of 5, 15, and 25 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
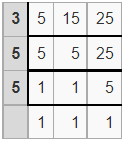
LCM = 3 x 5 x 5
Thus the least common multiple (L.C.M) of 5, 15, 25 = 75
Therefore, LCM(5, 15, 25) = 75
Example 8.
What is the least common multiple (L.C.M) of 10, 14, and 16 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
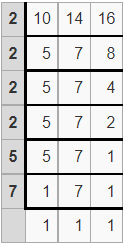
LCM = 2 x 2 x 2 x 2 x 5 x 7
Thus the least common multiple (L.C.M) of 10, 14 and 16 = 560
Therefore, LCM(10, 14, 16) = 560
Example 9.
What is the least common multiple (L.C.M) of 20, 30, and 60 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
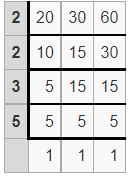
LCM = 2 x 2 x 3 x 5
Thus the least common multiple (L.C.M) of 20, 30 and 60 = 60
Therefore, LCM(20, 30, 60) = 60
Example 10.
What is the least common multiple (L.C.M) of 6, 18, and 30 by using the division method?
Solution:
Write your numbers in the top row.
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
Bring down any numbers that are not evenly divisible by the prime number.
When the last row of results is all 1’s you are done.
Find the product of the prime numbers in the first column to get the LCM:
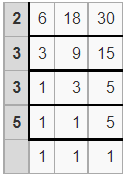
LCM = 2 x 3 x 3 x 5
Thus the least common multiple (L.C.M) of 6, 18 and 30 = 90
Therefore, LCM(6, 18, 30) = 90
