Multiplying two whole numbers gives a product. The numbers that we multiply are the factors of the product. The Examples on Factors on various questions are explained step by step. Know how to make use of the properties of factors from here and solve problems. Practice the given questions on finding factors using various methods such as prime factorization, factor tree, etc, and learn how to find factors of a number. Check your answers with the given solutions and test your knowledge.
Factor × Whole Number = Multiple
Do Refer:
Examples on Factors
Example 1.
What are the factors of 50?
Solution:
The factors of 50 are as follows
1 × 50
2 × 25
5 × 10
10 × 5
25 × 2
50 × 1
Thus the factors of 50 are 1, 2, 5, 10, 25, 50.
Example 2.
What are the factors of 74?
Solution:
The factors of 74 are as follows
1 × 74
2 × 37
37 × 2
74 × 1
Thus the factors of 74 are 1, 2, 37 and 74.
Example 3.
What are the common factors of 20 and 24?
Solution:
To find the common factors of 20 and 24 we have to write the factors of 20 and 24 first.
Factors of 20 are 1, 2, 4, 5, 10, 20.
Factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
Thus the common factors of 20 and 24 are 1, 2, 4.
Example 4.
Write the prime factors of 64.
Solution:
The prime factors of 64 are as follows
64 = 2 × 32
= 2 × 2 × 16
= 2 × 2 × 2 × 8
= 2 × 2 × 2 × 2 × 4
= 2 × 2 × 2 × 2 × 2 × 2
Thus the prime factors of 64 are 2, 4, 8, 16, 32 and 64.
Example 5.
Write the prime factors of 26.
Solution:
The prime factors of 26 are as follows
26 = 2 × 13
Therefore 2 and 13 are the prime factors of 26.
Example 6.
Check if 8 is a factor of 96.
Solution:
To check whether 8 is a factor of 96 we have to write the factors of 96.
The factors of 96 are as follows
1 × 96
2 × 48
3 × 32
4 × 24
6 × 16
8 × 12
16 × 6
24 × 4
32 × 3
48 × 2
96 × 1
Thus the factors of 96 are 1, 2, 3, 4, 6, 8, 12, 24, 32, 48, and 96.
Therefore we can say that 8 is a factor of 96.
Example 7.
Check whether 2 is a factor of 18.
Solution:
To check whether 2 is a factor of 18 we have to write the factors of 18.
The factors of 18 are as follows
1 × 18
2 × 9
3 × 6
6 × 3
9 × 2
18 × 1
Thus the factors of 18 are 1, 2, 3, 6, 9, 18.
Hence 2 is a factor 18.
Example 8.
Find the factors of 20 using the factor tree method.
Solution:
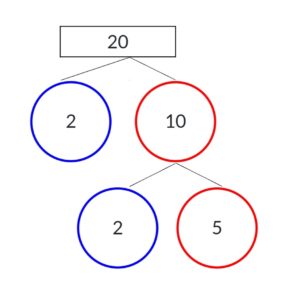
Factor tree of 20 is the list of prime numbers when multiplied results in the original number 20.
20 = 2 × 10
10 = 2 × 5
20 = 2 × 2 × 5
Example 9.
Find the factors of 36 using the factor tree method.
Solution:
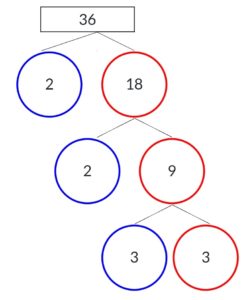
Factor tree of 36 is the list of prime numbers when multiplied results in the original number 36.
Split 36 until you get the prime numbers.
36 = 2 × 18
Split 18 into 18 = 2 × 9
Split 9 into 3 × 3
9 = 3 × 3
Factors of 36 are 2 × 2 × 3 × 3
Thus the prime factors of 36 are 2, 2, 3, 3
Example 10.
Write the prime factors of 15.
Solution:
The prime factors of 15 can be written as
15 = 3 × 5
Here 3 and 5 are the prime numbers.
Thus the prime factors of 15 are 3, 5.
Example 11.
Find the missing factors
i. 256 × _ = 256
ii. _ × 5 = 25
iii. 12 × _ = 60
Solution:
i. 256 × _ = 256
Let the missing factor be x
256 × x = 256
x = 256/256
x = 1
Thus the missing factor is 1.
ii. _ × 5 = 25
Let the missing factor be y.
y × 5 = 25
y = 25/5
y = 5
Thus the missing factor is 5.
iii. 12 × _ = 60
Let the missing factor be z.
12 × z = 60
z = 60/12
z = 5
Thus the missing factor is 5.
