The Highest Common Factor (H.C.F) of two numbers is the highest number among all the common factors of the given numbers. The HCF is also known as Greater Common Factor(GCF). Division Method, Prime Factorization Method, and Factorization methods are used to find the Highest Common Factor of the given numbers.
For better understanding, we’ve covered various questions with a quick explanation here. In this article, we have covered different methods questions on HCF to enhance their math skills as well as provide you better practice. You just need to solve the HCF Problems available on this page and test your conceptual knowledge.
Also, Read Some More Article:
HCF Example Problems
Example 1:
Find the Highest Common Factor of 45 and 50.
Solution:
As given in the question the values are 45 and 50.
The factors of 45 are 1, 3, 5, 9.
The factors of fifty are 1, 2, 5, 10
So, the Common Factors of 45 and 50 are 1, 5.
Therefore, the Common Highest Factor among them is 5.
Example 2:
What is the HCF of 18 and 36 using the Prime Factorization Method?
Solution:
Given the values 18 and 36.
Using Prime Factorization Method, we can find the HCF value.
The Prime Factorization of 18 is 2 x 9
The Prime Factorization of 36 is 2 x 2 x 9
So, the common factors of 18 and 36 are 2 x 9
Thus, the HCF of the two given numbers is 2 x 9 is 18.
Example 3:
What is the Highest Common Factor of 28 and 44 using the Factorization method?
Solution:
As given the values are 28 and 44.
Using the Factorization method, to find the HCF value.
The factor of 28 are 1, 2, 4, 14
The factors of 44 are 1, 2, 4, 11, and 44.
So, the common factors of given numbers are 1, 2, 4.
Thus, the Highest Common Factor of 28 and 44 is 4.
Example 4:
Find the possible numbers. The HCF of the two numbers is 29 and their sum is 174.
Solution:
Given the HCF of the two numbers is 29 and their sum is 174.
Now, we will find the possible numbers.
Let the numbers be
29(a+b) = 174 (or) 27a + 27b = 174
So, a +b = 174/ 29 = 6.
The values of co-primes with sum 6 is 1,5
Therefore, the possible pairs of numbers are 29 x 1, and 29 x 5. It will become the 29 and 145.
Thus, the possible numbers are 29 and 145.
Practice Math Online with Unlimited Questions provided in 5th Grade Math Activity Sheets and become a blossoming mathematician in no time.
Example 5:
Find the HCF of 65, 45 using the division method and leaving 5 as the remainder?
Solution:
Given,
The number divides 65 and leaves 5 as the remainder.
So, the number divides 65 – 5 = 60 exactly.
The number divides 45 and leaves 5 as the remainder.
So, the number divides 45 – 5 = 40 exactly.
Now, we have to find the HCF(60, 40)
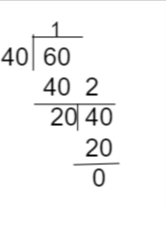
Therefore, the HCF of a given number 65, 45 is 20.
Example 6:
Find the HCF OF 9, 84 using the Division Method?
Solution:
Given the value is 9, 84
Using the division Method, we will find the value.
First, divide 9 and 84. So, 9 will be the divisor and 84 will be dividend
Now the remainder will become the new divisor and 9 will become the new dividend.
Proceed with this process till the remainder is zero and the last divisor will be the HCF of the given number.
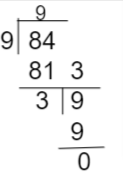
Thus, the HCF of 9, 84 using the Division Method is 3.
Example 7:
Find the Highest Common Factor 6, 72, 26 using the Prime Factorization Method.
Solution:
As given in the question, the values are 6, 72, 26.
Now, we will find the HCF value using the Prime Factorization Method.
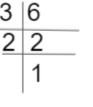
The factors of 6 are 1, 2, and 3.
Next, 72 factors are

So, the factors of 72 are 1, 3, and 4.
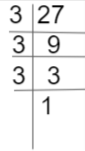
The factors 27 are 1, 3
So, the common factors of 6, 72, 27 are 1, 3.
Thus, the Highest Common Factor among them is 3.
Example 8:
Find the Highest Common Factors of the following using Factorization,
(i) 81, 99
(ii) 47, 63
Solution:
(i) Given the values 81, 99
Using factorization, we will find the values.
The factors of 81 are 1, 3, 9
The factors of 99 are 1, 3, 9, 11.
The common factors are 1, 3, 9.
Therefore, the Highest Common Factor of the given numbers is 9.
(ii) Given the values are 47, 63
Using factorization, we will find the values.
The factors of 47 are 1, 7.
The factors of 63 are 1, 3, 7, 9, and 63.
The common factors are 1, 7.
Therefore, the Highest Common Factor of the given numbers is 7.
Example 9:
Find the H.C.F. of three numbers 44, 48, 52 by the prime factorization method.
Solution:
Given the values are 44, 48, 52.
Using the prime factorization method, we have to find the factors.
First, we have to write down the factors of the given numbers.
The factors of 44 are 1, 2, 4, 11.
The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24.
The factors of 52 are 1, 2, 4, 5,12, 13, and 52.
Now, we have to write the common factors of all three numbers.
Common factors of 44, 48, 52 is 1, 2, 4.
Thus, the HCF of three numbers of given numbers is 4.
Example 10:
John has 16 red pens and Ryan has 24 green pens. They want to arrange the pens in such a way that each row contains an equal number of pens and also each row should have only red pens or green pens. What is the greatest number of pens that can be arranged in each row?
Solution:
As given in the question,
Now, find the highest number of pens which will be arranged in equal rows, we have to seek out the HCF of two numbers.
The factors of 16 are 1, 2, 4, 8, and 16.
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
The common factors are 1, 2, 4, 8. The highest common factor among them is 8.
Therefore, the greatest number of pens that can be arranged in each row is 8.
FAQ’s on HCF Example Questions
1. What are the methods used for finding the HCF?
There are three methods to find H.C.F of two or more numbers
1. Division Method
2. Factorization method
3. Prime Factorization method
2.What’s Highest Common Factor?
It is the Highest of the common factor of two or more given numbers. It is also named Greatest Common Divisor(GCD).
3. How do we use Highest Common Factor?
The HCF is used to simplify the fractions. The Highest Common Factor (HCF) or GCD is that the greatest number that divides exactly into two numbers.
