Everyday Mathematics 6th Grade Answer Key Unit 8 Applications: Ratios, Expressions, and Equations
Everyday Mathematics Grade 6 Home Link 8.1 Answers
Increasing Yield per Square Foot
The diagram below shows the layout of a garden that has both rows and squares.
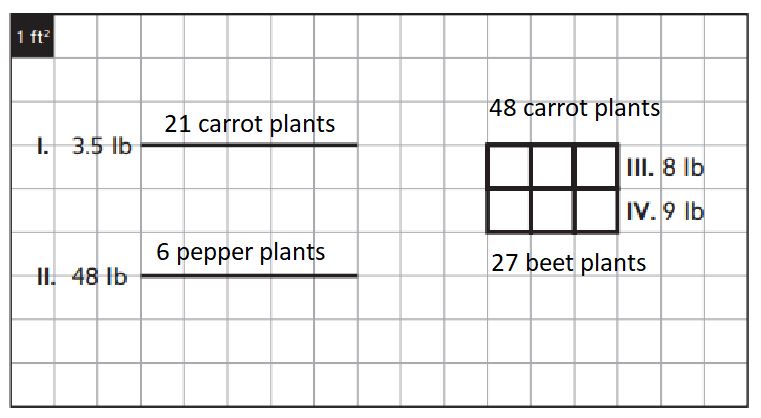
Use the yields on the diagram and the table information to determine which plant is in each row or square foot.
Question 1.
Label each garden bed to show what kind of plant and how many of the plants fill the row or square foot.
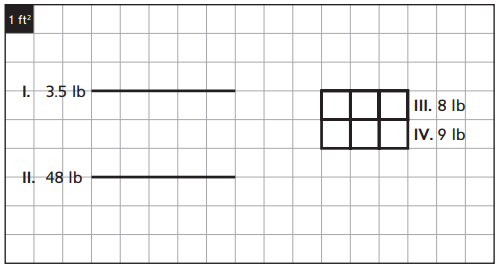
Answer:
Question 2.
a. What is the total expected yield for the garden in Problem 1? ____________
b. What is ? ____________
Answer:
a. The total expected yield for the garden in problem 1 is 68.5 pounds
b. The overall rate of plants per square foot is about 2/3 plant to 1 ft 2
Question 3.
a. About how much more should the garden yield if beds I and II are changed from row garden beds to square-foot garden beds? (Assume the same plant would still be planted in each.) ____________
b. What would the overall rate of plants per square foot be? ____________
Answer:
a. About 2 more pounds should the garden yield if beds I and II are changed from row garden beds to square-foot garden beds.
b. The overall rate of plants per square foot is is 1 plant to 1 ft 2
Practice
Solve the equations.
Question 4.
\(\frac{1}{2}\)p = 87; p = ________
Answer:
174
Explanation :
1/2 x p = 87
p = 87 x 2 = 174
Therefore, the value of p is 174
Question 5.
\(\frac{2}{3}\)d = 56; d = __________
Answer:
84
Explanation :
2/3 x d = 56
d = 56 x 3 / 2
d = 28 x 3 = 84
Therefore, the value of d is 84
Question 6.
\(\frac{7}{8}\)k = 84; k = __________
Answer:
96
Explanation :
7/8 x k = 84
k = 84 x 8 /7
K = 12 x 8 = 96
Therefore, the value of k is 96
Everyday Math Grade 6 Home Link 8.2 Answer Key
Question 1.
Using Scale Drawings Julian made a scale drawing of his bedroom wall. He has artwork that he and his brother made hanging on the wall. His wall is 7 feet high and 12 feet long.
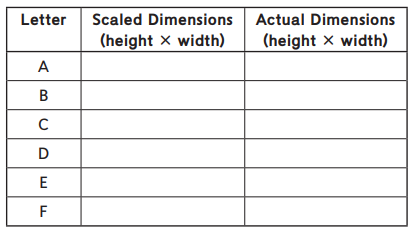
a. What scale did he use? ________
b. Use his scale drawing to complete the table.
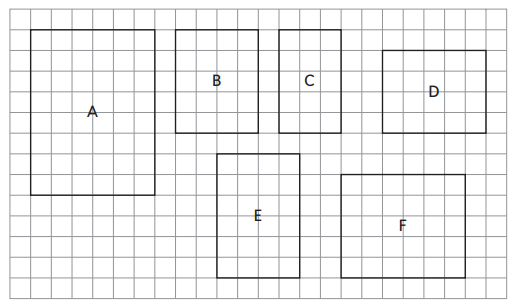
Answer:
a. The scale he used is 1/2 inch equals to 1 foot ( 1/2 inch = 1 foot )
b.
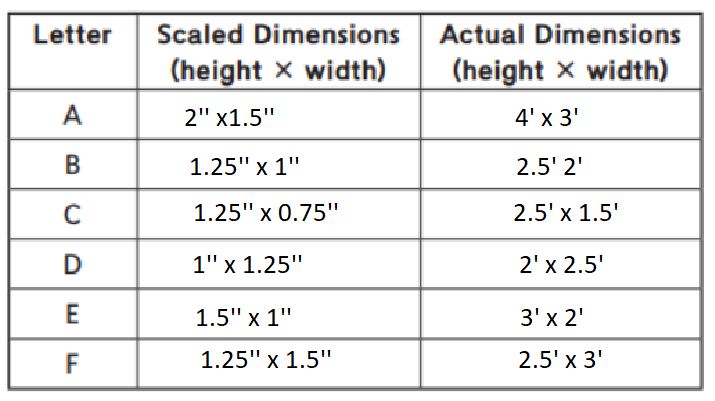
Question 2.
Explain how you found the actual dimensions for Artwork B.
_______________________
______________________
Answer:
2 Squares = 1 foot
4 Squares = 2 feet
So, 5 squares = 25 Feet
Question 3.
Why might someone make a scale drawing of a planned artwork arrangement?
_______________________
________________________
Answer:
To make sure that result is so perfect and so accurate.
Practice Solve.
Question 4.
15% of x is 6. 100% of x is ________
Answer:
40
Explanation :
15 % = 15/100
Given,
15% of x is 6
= 15/100 X x -= 6
x = 100 X 6 /15
x = 40
And 100% = 100/100 = 1
Therefore, 100% of 40 is 1 x 40 = 40.
Question 5.
90% of y is 18. 100% of y is ________.
Answer:
20
Explanation:
90% = 90/100
Given,
90% of y is 18
= 90/100 X y = 18
y = 18 X 100 /90
y = 20
And 100% = 100/100 = 1
Therefore, 100% of 20 is 1 X 20 =20
Everyday Mathematics Grade 6 Home Link 8.3 Answers
Stretching Triangles
Question 1.
Plot the original ordered pairs from the table in Problem 2, and connect points to make triangle ABC and triangle ADE.
Answer:
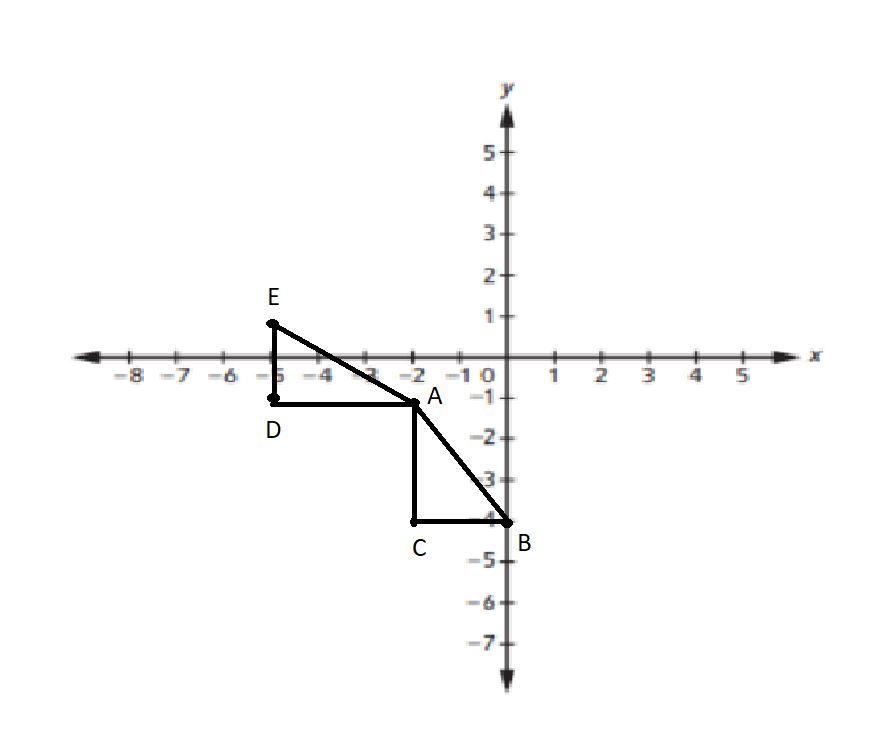
Question 2.
If you want to make triangle ABC and triangle ADE twice as tall and twice as wide, what would the new coordinates be? Write them in the table below.
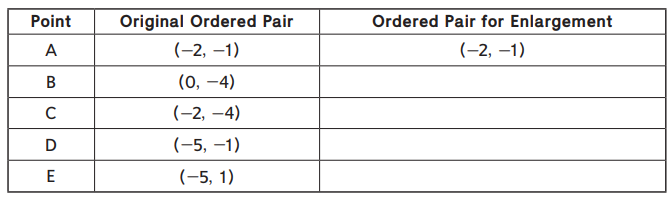
Answer:
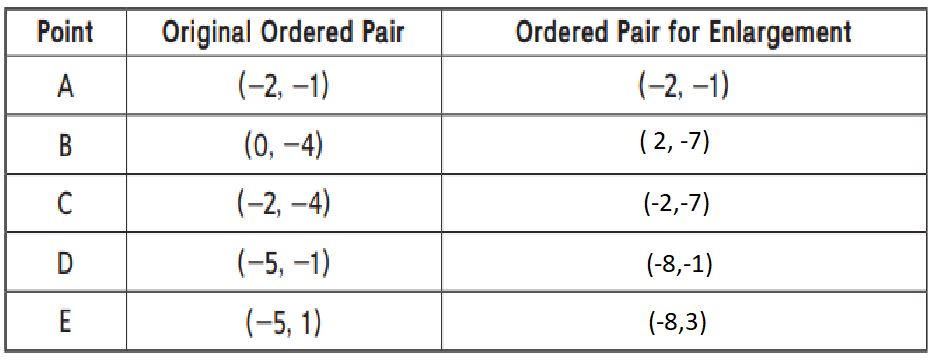
Question 3.
What is the distance from D to E in the enlarged figure? ________
Answer:
The distance from D to E in the enlarged figure is 4 units
Question 4.
What is the distance from D to E in the original figure? __________
Answer:
The distance from D to E in the original figure is 2 Units
Question 5.
Use ratio notation to represent the ratio of side length \(\ over line{D E}\) in the enlarged figure to side length \(\over line{D E}\) in the original figure. _______
Answer:
2 :1
Practice Solve.
Question 6.
\(\frac{3}{4}\) (4 – \(\frac{2}{3}\)) = _______
Answer:
3/4 X [4-2/3]
3/4 X[ 10/3]
= 5/2
Question 7.
3 + \(\frac{1}{2}\) ÷ 3 = ________
Answer:
3 + [ 1/2 / 3]
3 + [1/6]
= 19/6
Question 8.
______ = 2\(\frac{1}{2}\) ÷ (\(\frac{4}{3}\) – \(\frac{1}{2}\))
Answer:
[5/2] / (4/3-1/2)
[5/2] / ( 5/6)
= 3
Everyday Math Grade 6 Home Link 8.4 Answer Key
Modeling Distances in the Solar System
Today the class made scale models of celestial bodies.
Imagine you are modeling the distance of each planet from the Sun.
Question 1.
Calculate the distance from the Sun in your model using the scale given in the table. Complete the table.
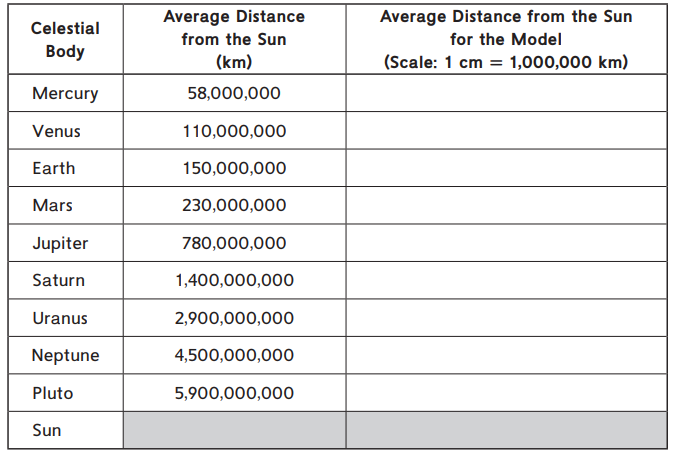
Answer:
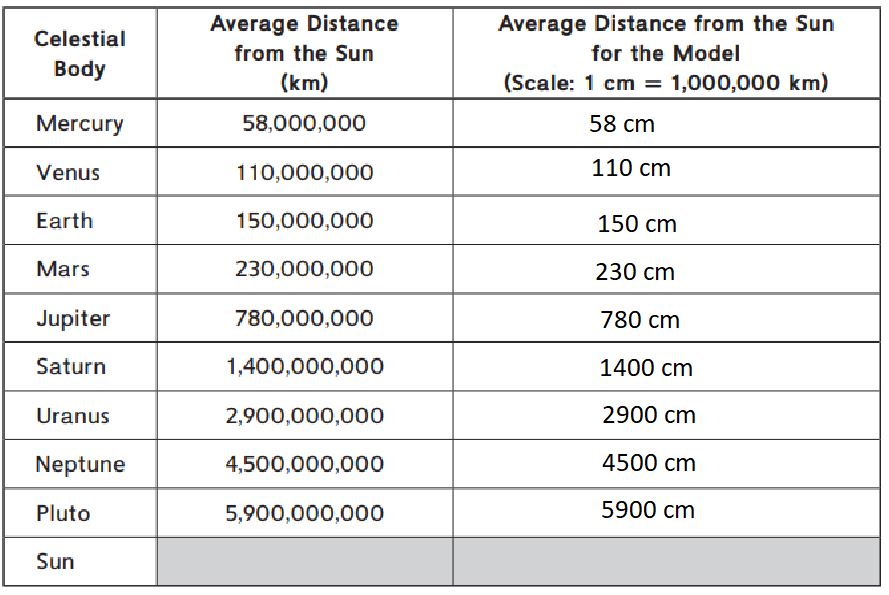
Question 2.
Would this scale work for building the model in your classroom? Why or why not?
_____________________________
______________________________
Answer:
No, this scale not work for building the model in our classroom. Because, this scale is too large for the distances.
Question 3.
What scale for distance might work for a model in your classroom?
___________________________________
Answer:
The scale for distance might work for a model in our classroom is
1 cm = 10 million kilometres
Practice
Solve.
Question 4.
\(\frac{t}{12}\) = 8 ______
Answer:
t/12 =8
t = 8 X 12
Therefore, t = 96
Question 5.
p ÷ 9 = 11 _______
Answer:
p/9 =11
p= 99
Question 6.
n + 0.35 = 5 ________
Answer:
n+0.35 = 5
n = 4.65
Everyday Mathematics Grade 6 Home Link 8.5 Answers
Comparing Player Density
The dimensions of the playing surfaces for four sports are listed below.
Football: 360 ft by 160 ft
Hockey: 200 ft by 85 ft (Ignore round corners)
Basketball: 50 ft by 94 ft
Baseball: 108,500 ft2 (Average for major league parks)
During a game, there are 22 players on a football field, 10 on a basketball court, 10 on a baseball diamond (not counting base runners), and 12 on an ice hockey rink. Calculate the square feet of playing area per player for each sport.
Question 1.
Football playing area: ___________
Area per player: ____________
Answer:
Football playing area is 57,600 Square feet
Area per player is 2618 Square feet
Question 2.
Basketball playing area: ____________
Area per player: ____________
Answer:
Basketball playing area is 4700 Square feet
Area per player is 470 Square feet
Question 3.
Hockey playing area: ____________
Area per player: ____________
Answer:
Hockey playing area is 17,000 Square feet
Area per player is 1417 Square feet
Question 4.
Baseball playing area: ____________
Area per player: ____________
Answer:
Baseball playing area is 108,500 Square feet
Area per player is 10,850 Square feet
Question 5.
a. Which sport is the most “crowded”? ____________
b. Justify your answer. ____________
Answer:
a. Basket ball is the sport is most crowded
b. Number of players are same as other sports even though Basketball has the smallest area. Hence, Basketball is most crowded.
Question 6.
Describe the relationship between square feet per player and player density.
__________________________
Answer:
The relationship between square feet per player and player density is “the number of square feet per player is directly proportional to spread of the player ” means the larger the number of square feet per player, the more spread of the players.
Question 7.
If the player density is lower, how might that affect their role in the game?
___________________________
Answer:
The team in which the player density is low , then it’ll be in a chance of losing side. Hence, it is the responsibility of each player to cover more of the playing the field.
Practice Simplify the expressions.
Question 8.
7t – 4t ________
Answer:
7t-4t = 3t
Question 9.
5 + 7r – 1.5 – 2r _______
Answer:
5 + 7r – 1.5 – 2r
(5-1.5) +(7r-2r)
3.5+5r
Question 10.
9(3c) ______
Answer:
27c
Question 11.
\(\frac{1}{2}\) (4b + 12) _______
Answer:
1/2 (4b/12)
(4b/2)/(12/2)
2b/6.
Everyday Math Grade 6 Home Link 8.6 Answer Key
Mobiles
The mobiles shown in Problems 1 and 2 are in balance.
All measures are in feet for distances or pounds for weight.
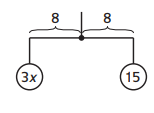
Question 1.
What is the weight of the object on the left of the fulcrum?
W = __________
D = _________
w = _________
d = _________
Equation: _________
Solution: _________
Weight: _________
Answer:
W = 3x
D = 8
w = 15
d = 8
Equation : (3x)8 =(15)8
Solution: x = 15 ,5
Weight:
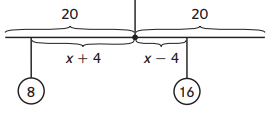
Question 2.
What is the distance of each object from the fulcrum?
W = _________
D = _________
w = _________
d = _________
Equation: _________
Solution: _________
Distance on the left of the fulcrum: _________
Distance on the right of the fulcrum: _________
Answer:
W = 8
D = x+4
w = 16
d = x-4
Equation: 8(x+4) = 16(x-4)
Solution: x=12
Distance on the left of the fulcrum: 16 lb
Distance on the right of the fulcrum: 8 lb
Question 3.
a. Sketch a mobile that will balance.
Label all lengths and weights.
Answer:
b. Use the mobile formula to explain why your mobile balances.
Answer:
Practice
Divide.
Question 4.
34.5 ÷ 0.5 = ______
Answer:
69
Question 5.
8.46 ÷ 4.7 = _______
1.8
Answer:
Question 6.
______ = 1.22 ÷ 4
Answer:
0.305
Question 7.
______ = 26.88 ÷ 0.48
Answer:
56
Everyday Mathematics Grade 6 Home Link 8.7 Answers
Generalizing Patterns
Question 1.
Use the pattern pictured below. Shade a constant part of the pattern.
a. In the table, record numeric expressions for the total number of squares that represent what is shaded and how the pattern is growing.
Plan your numeric expressions to show one part of the expression as constant and the other part as varying.
b. Write an algebraic expression for the number of squares in Step n.
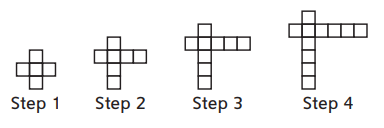
Answer:
a.
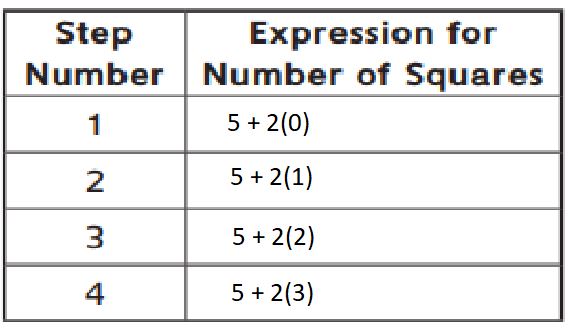
b.
an algebraic expression for the number of squares in Step ‘n’ is 5+2(n-1)
Question 2.
Circle an expression for finding the number of squares needed to build Step n that best represents how the pattern is shaded.
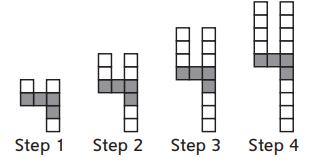
3 + 2n + n + 1
4 + 3n
6 + n + 2(n – 1)
7 + 3(n – 1)
Answer:
3+2n+n+1
Question 3.
Explain why the expression you chose in Problem 2 is the best match.
Answer:
The expression 3+2n+n+1 is best match because it is showing the third (3rd) row is shaded and also showing that multiple of 2 is added on top and also the number added at the bottom also the same number shaded at bottom.
Practice Simplify.
Question 4.
5(x + 10) = ______
Answer:
5x+50
Question 5.
2(x + 8) = _______
Answer:
2x+16
Question 6.
6x + 2x = _____
Answer:
8x
Everyday Math Grade 6 Home Link 8.8 Answer Key
Using Anthropometry
The following passage is from Gulliver’s Travels by Jonathan Swift. The setting is Lilliput, a country where the people are only 6 inches tall. “Two hundred seamstresses were employed to make me shirts . . . . The seamstresses took my measure as I lay on the ground, one standing at my neck, and another at my mid leg, with a strong cord extended, that each held by the end, while the third measured the length of the cord with a rule of an inch long. Then they measured my right thumb and desired no more; for by a mathematical computation, that twice round the thumb is once round the wrist, and so on to the neck and the waist, and by the help of my old shirt, which I displayed on the ground before them for a pattern, they fitted me exactly.”

Question 1.
Four body parts are referenced in the text. What are they?
Choose a variable to represent each one.
Answer:
Four body parts are Neck (N) , Leg (L) , Thumb(T) , Waist(W)
Question 2.
Take these four measures on yourself, measuring to the nearest \(\frac{1}{4}\) inch.
Answer:
The four measurements are 1/4, 2/4, 3/4, 4/4.
Question 3.
Use the variables you recorded in Problem 1 to write three rules described in the text.
Answer:
The three rules are W=2T ; N=2W ; L=2N
Question 4.
Based on your data, how well do you think Gulliver’s new clothes fit? Explain.
Answer:
Being the measurements are by a mathematical computation, the measurements are accurately and fit exactly for Gulliver.
Practice
Evaluate.
Question 5.
5 \(\frac{1}{2}\) ÷ \(\frac{1}{4}\) = ________
Answer:
22
Question 6.
______ = 2 \(\frac{2}{3}\) ÷ \(\frac{3}{4}\)
Answer:
32/9
Everyday Mathematics Grade 6 Home Link 8.9 Answers
Which Would You Rather Have ?
Don’s boss is offering him two choices to get paid for June.
- Choice #1 is to receive $10 on June 1st, $20 on June 2nd, $30 on June 3rd, and so on through June 30th.
- Choice #2 is to receive 1 penny the first day, 2¢ the second day, 4¢ the third day, and so on, doubling the amount each day for the rest of the month.
Question 1.
a. Predict which is the better plan. _________
b. Explain how you made your choice. ___________
Answer:
a.
Choice 1
b.
Because, at the end of the month, total will be higher in first case when compared to second case
Question 2.
Enter formulas to complete the table for the first five days of each plan.
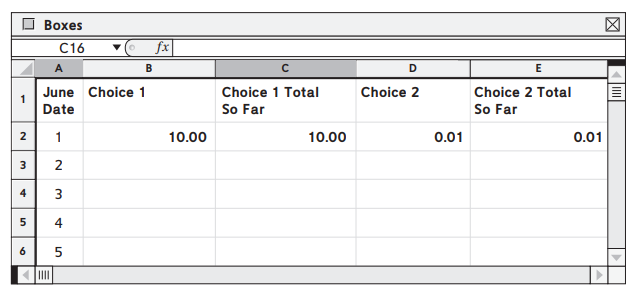
Answer:
for choice 1 : 10x
for second case : (0.01)(2^(x-1))
Question 3.
Use a spreadsheet program or a calculator to determine how much Don would receive for the day on June 30th for each choice.
Choice 1: _________
Choice 2: _________
Answer:
Choice 1: $300
Choice 2: 5,368,709.12
Question 4.
If you have a spreadsheet program, find the total amount Don receives for both choices. If you do not, explain how to find the totals on the back of this page
Choice 1: _________
Choice 2: ________
Answer:
Choice 1: $4,650
Choice 2: $10,737,418.23
Practice
Write three equivalent ratios for each ratio.
Question 5.
2.5 to 2 ______
Answer:
1.25:1 , 5:4 , 10:8
Question 6.
1 : 1.4 ________
Answer:
2:2.8 , 20:28 , 40:56
Question 7.
\(\frac{1}{2}\) to 3 _______
Answer:
1:6 , 2:12 , 5:30
Question 8.
\(\frac{1}{2}\) : \(\frac{3}{4}\) _______
Answer:
1:1.5 , 2:3 , 4:6