Everyday Mathematics 6th Grade Answer Key Unit 5 Area and Volume Explorations
Everyday Mathematics Grade 6 Home Link 5.1 Answers
Polygon Side Lengths
Question 1.
Find any missing coordinates. Plot and label the points on the coordinate grid. Draw the polygon by connecting the points.
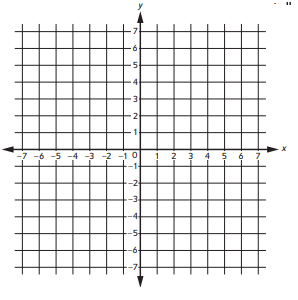
a. Rectangle ABCD
A: (1, 1) B: (-1, 1)
The length of \(\overline{B C}\) is represented by
|1| + |-4| = _______.
C: (_______, _______)
D: (_______, _______)
Answer:
b. Right triangle XYZ
X: (-5, 1) Z: (-3, 6)
The length of \(\overline{Z Y}\) is represented by |6| – |1| = _______.
The length of \(\overline{X Y}\) is represented by |-5| – |-3| = _______.
Y: (_______, _______)
Answer:
Question 2.
Use rectangle ABCD and triangle XYZ to fill in the following tables. The first row has been done as an example.
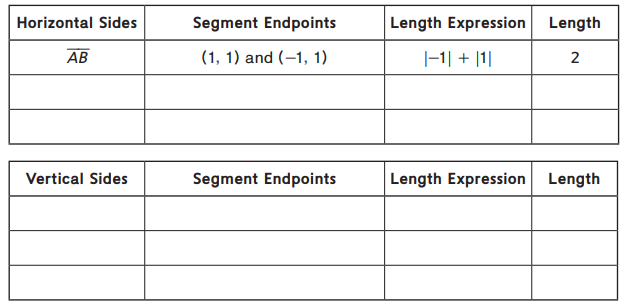
Answer:
Practice
Divide.
Write any remainders using R.
Question 3.
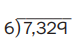
Answer:
Question 4.
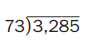
Answer:
Question 5.
![]()
Answer:
Question 6.
![]()
Answer:
Everyday Math Grade 6 Home Link 5.2 Answer Key
Finding the Areas of Parallelograms
Find the area of each parallelogram. Show your work.
Question 1.
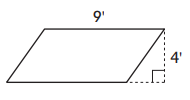
Area: ___________
Answer:
Question 2.
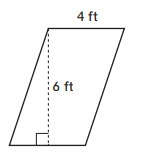
Area: ___________
Answer:
Question 3.
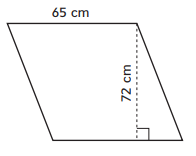
Area: ___________
Answer:
Question 4.
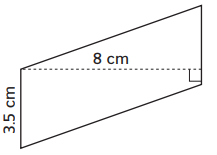
Area: ___________
Answer:
Try This
The area of each parallelogram is given. Find the length of each base.
Question 5.

Area: 26 square inches
Base: ___________
Answer:
Question 6.
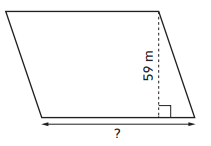
Area: 5,015 square meters
Base: ___________
Answer:
Practice
Evaluate.
Question 7.
20% of 45 ________
Answer:
Question 8.
45% of 60 ________
Answer:
Question 9.
83% of 110 ________
Answer:
Everyday Mathematics Grade 6 Home Link 5.3 Answers
Triangle Area
Find the area of each triangle. Remember: A = \(\frac{1}{2}\)bh.
Question 1.
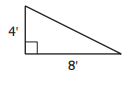
Number model: _________
Area = _________
Answer:
Question 2.
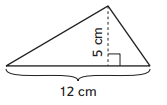
Number model: _________
Area = _________
Answer:
Question 3.
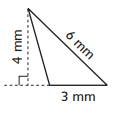
Number model: _________
Area = _________
Answer:
Question 4.
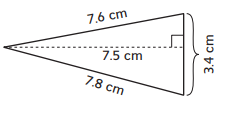
Number model: _________
Area = _________
Answer:
Question 5.
Find the length of the base.
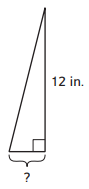
Area = 18 in.2
Base = _________
Answer:
Try This
Question 6.
Draw a height for the triangle. Find the length of the height.
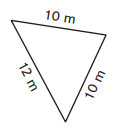
Area = 48 m2
Height = _________
Answer:
Practice
Compute.
Question 7.
|-7| = ____
Answer:
Question 8.
|4| = ____
Answer:
Question 9.
______ = |-3|
Answer:
Everyday Math Grade 6 Home Link 5.4 Answer Key
Areas of Complex Shapes
In Problems 1–4, decompose the shapes into polygons for which area formulas can be used. Label the areas. Find the total area for each shape. Use appropriate units.
Question 1.
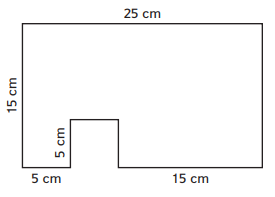
Area: ________
Answer:
Question 2.
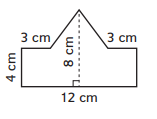
Area: ________
Answer:
Question 3.
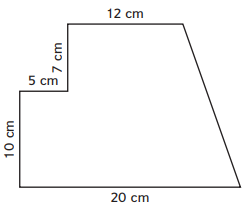
Area: ________
Answer:
Try This
Question 4.
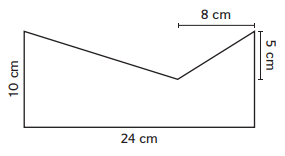
Area: ________
Answer:
Practice
Calculate.
Question 5.
12 – 8.25 = ________
Answer:
Question 6.
_______ = 9.03 + 0.7 + 18
Answer:
Question 7.
125.29 – 16.7 = ______
Answer:
Question 8.
_______ = 0.01 + 0.99
Answer:
Everyday Mathematics Grade 6 Home Link 5.5 Answers
Real- World Nets
Circle the solid that can be made from each net.
Question 1.

Answer:
Question 2.
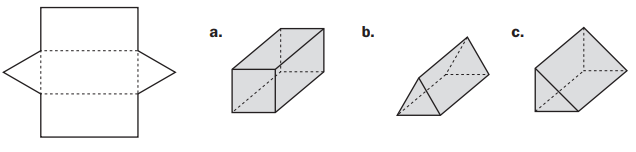
Answer:
Question 3.
Use the net and its corresponding geometric solid in Problem 2.
a. Which polygons make up the faces of your solid? How many are there of each kind? __________
b. Which faces are parallel? __________
c. Which faces are congruent? __________
d. How many edges are there? How many vertices? __________
Answer:
Practice
Multiply.
Question 4.
5.2 ∗ 3 = ______
Answer:
Question 5.
1.04 ∗ 2 = ______
Answer:
Question 6.
______ = 0.14 ∗ 3
Answer:
Everyday Math Grade 6 Home Link 5.6 Answer Key
Surface Area Using Nets
Silly Socks is trying to choose a type of plastic box for their socks. The nets for three different box designs are given below.
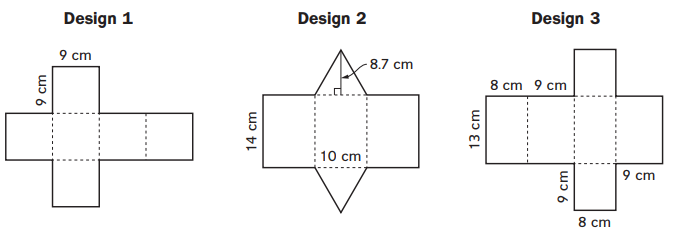
Question 1.
Without calculating, predict which design will require the least amount of plastic to produce.
Answer:
Question 2.
Find the surface area for each plastic-box design. Write a number sentence to show how you found the surface area. Remember to use the correct order of operations.
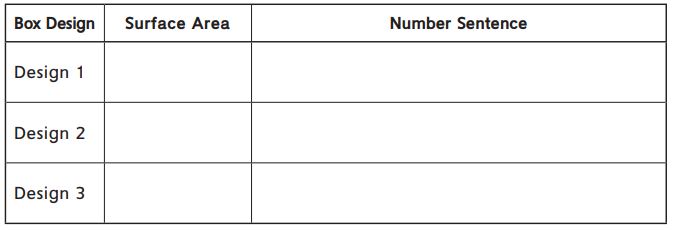
Answer:
Question 3.
Explain how to find the surface area for any rectangular or triangular prism.
Answer:
Practice
Divide. Find your answer to the nearest hundredth.
Question 4.
![]()
Answer:
Question 5.
![]()
Answer:
Question 6.
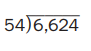
Answer:
Everyday Mathematics Grade 6 Home Link 5.7 Answers
Surface Area
Question 1.
Sam is painting the outside of a doghouse dark green (except for the bottom, which is on the ground).
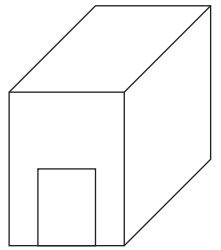
The doghouse measures 3 feet wide by 4.5 feet long. It is 4 feet high.
The roof is flat, so the doghouse looks like a rectangular prism.
The entrance to the dog house is 1.5 feet wide by 2 feet high.
a. Label the doghouse diagram with the measurements.
Answer:
b. On the grid below, draw a net for a prism that could represent Sam’s doghouse.
Scale: ☐ = 1 square foot

Answer:
c. How many square feet is he painting?
Answer:
d. One pint of paint covers about 44 ft2. How many pints does he need?
Answer:
Practice
Evaluate.
Question 2.
43 ______
Answer:
Question 3.
1.52 _______
Answer:
Question 4.
150 ______
Answer:
Question 5.
(\(\frac{2}{3}\))2 ______
Answer:
Everyday Math Grade 6 Home Link 5.8 Answer Key
Arguing about Areas
Jayson was comparing the areas of the polygons at the right.
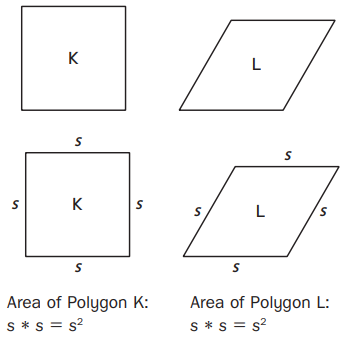
Here is Jayson’s reasoning: I think that Polygons K and L have the same area. I lined up the sides of each polygon and they were equal, so I labeled the sides with the same variables. So the area of Polygon K is equal to the area of Polygon L.
Question 1.
Explain the flaw in Jayson’s reasoning.
Answer:
Trace Polygon K above, and cut out your tracing. Use it to help you solve Problems 2–3.
Question 2.
Draw two different polygons that have the same area as PolygonK.
Answer:
Question 3.
Choose one of your polygons from Problem 2. Describe how you used Polygon K to draw a polygon that has the same area.
Answer:
For Lesson 5-9, bring a rectangular prism, such as an empty tissue box, to class.
Practice
Find the whole.
Question 4.
10% is 7, so 100% is ______.
Answer:
Question 5.
25% is 90, so 100% is _______.
Answer:
Everyday Mathematics Grade 6 Home Link 5.9 Answers
Volume of Rectangular Prisms
Find the volume for each prism.
Question 1.
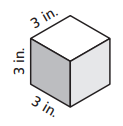
Volume ________
Answer:
Question 2.
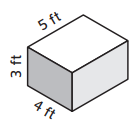
Volume _______
Answer:
Question 3.
The Blueberry Blast cereal box is a rectangular prism that is 12 inches × 8 inches × 4 inches.
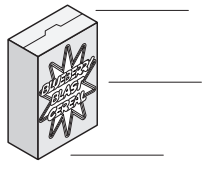
a. Label the diagram with the dimensions.
b. What is its volume?
Answer:
Question 4.
Greta’s gift shop has three sizes of gift boxes. They are all shaped like rectangular prisms. The dimensions are shown below.
Small: 10 cm × 10 cm × 10 cm
Large: 40 cm × 30 cm × 15 cm
Medium: The area of the base is 1,000 cm2 and the height is 8 cm.
Find the volume of each gift box
Small: ________
Large: ________
Medium: ________
Answer:
Practice
Evaluate
Question 5.
\(\frac{2}{3}\) + \(\frac{5}{6}\) = ________
Answer:
Question 6.
4\(\frac{3}{4}\) + \(\frac{7}{8}\) = _________
Answer:
Question 7.
\(\frac{4}{5}\) – \(\frac{3}{4}\) = _________
Answer:
Question 8.
10 – \(\frac{5}{12}\) = __________
Answer:
Everyday Math Grade 6 Home Link 5.10 Answer Key
Calculating Luggage Volume
You may want to consider how much volume your luggage holds when you travel. If you know how to calculate the area of a rectangular prism, you can also find the approximate volume of a suitcase. Below are the measurements of some common suitcase sizes.

Question 1.
a. Find the volume of each suitcase.
Answer:
b. Find the approximate volume of the interiors. Round to the nearest 0.01 in.3.
Answer:
Suitcase 1
Exterior: 17″ × 15″ × 8″
a. Volume: __________
Interior: 16″ × 13.75″ × 6.5″
b. Volume:__________
Suitcase 2
Exterior: 21″ × 14″ × 7″
a. Volume: __________
Interior: 19.5″ × 13″ × 5.75″
b. Volume: __________
Suitcase 3
Exterior: 24″ × 16″ × 9.75″
a. Volume: __________
Interior: 22.5″ × 14.75″ × 8.25″
b. Volume: __________
Suitcase 4
Exterior: 28″ × 19″ × 9″
a. Volume: __________
Interior: 26″ × 17.5″ × 7.5″
b. Volume: __________
Question 2.
Describe how you can estimate the interior volume of a suitcase if you know the exterior measurements.
Answer:
Practice
Evaluate.
Question 3.
\(\frac{2}{3}\) ÷ \(\frac{1}{6}\) = ________
Answer:
Question 4.
\(\frac{5}{12}\) ÷ \(\frac{7}{12}\) = _________
Answer:
Question 5.
_________ = 2\(\frac{2}{3}\) ÷ \(\frac{1}{2}\)
Answer:
Question 6.
8 ÷ 2\(\frac{2}{3}\) = ____________
Answer:
Everyday Mathematics Grade 6 Home Link 5.11 Answers
Volume of Letters
The Santiago Balloon Emporium sells custom balloons shaped like letters of the alphabet. Clarissa orders balloons that spell DOLLIE for her friend’s birthday. She wants the balloons to float, so she plans to fill them with helium. To estimate how much it will cost, Clarissa needs to calculate the approximate volume of helium she will need to fill the balloons.
The volume of each balloon can be estimated based on rectangular prisms.

Measure the dimensions in millimeters for each rectangular part of the letters.
Question 1.
The scale is 1 mm = 1 inch. Each letter has a depth of 5 inches. Estimate the volume of each letter.
D: _________ O: _________ L:_________
I: _________ E: _________
Answer:
Question 2.
What is the approximate total volume of helium (in cubic inches) needed to fill the letters?
Answer:
Question 3.
a. Helium comes in tanks that hold either 8.9 ft3, which cost $19.99 each, or 14.9 ft3, which cost $28.99 each. What is the least amount Clarissa can spend to fill her letters with helium? Hint: There are 1,728 in.3 in 1 ft3.
Answer:
b. Explain how you found your answer to Part a.
Answer:
Practice
Divide.
Question 4.
![]()
Answer:
Question 5.
![]()
Answer:
Question 6.
![]()
Answer:
Question 7.
![]()
Answer:
Everyday Math Grade 6 Home Link 5.12 Answer Key
Could a Giant Breathe?
Think about how area and volume change in relation to changes in linear measurements.
Question 1.
How many centimeters are in 1 meter? ____________
Answer:
Question 2.
How many square centimeters are in 1 square meter? ____________
Answer:
Question 3.
How many cubic centimeters are in 1 cubic meter? ____________
One cubic centimeter of water has a mass of about 1 gram.
Answer:
Question 4.
One cubic meter of water has a mass of:
____________ grams ____________ kilograms
Answer:
Question 5.
One kilogram has a weight equivalent to about 2.2 pounds.
One cubic meter of water weighs about how many pounds? ____________
Answer:
Oxygen enters your body through the surface area of your lungs.
Question 6.
A giant who is 10 times as tall as you would have lungs that provide ____________ as much oxygen as your lungs.
Answer:
Question 7.
If the surface area of the giant’s lungs were 100 times greater than yours, and if the giant required oxygen in the same proportions as a human, how do you know the giant would not have enough oxygen? Explain.
Answer:
Try This
Question 8.
Your lungs fit in a relatively small space inside your rib cage. Research how your lungs increase surface area to be able to supply all the oxygen you need.
Answer:
Practice
For Problems 9–10 , record the opposite of the number.
Question 9.
-7 _______
Answer:
Question 10.
0 ______
Answer:
Question 11.
The opposite of the opposite of -3 ________
Answer: