Everyday Mathematics 6th Grade Answer Key Unit 2 Fraction Operations and Ratios
Everyday Math Grade 6 Home Link 2.1 Answer Key
Finding the Greatest Common Factor
Question 1.
Use any method to find the greatest common factor for the number pairs.
a. GCF (42, 56) = ___
b. GCF (32, 80) = ___
c. GCF (72, 16) = ___
d. GCF (10, 40, 25) = ____
Answer:
a. GCF of 42 and 56 = 14.
b. GCF of 32 and 80 = 16.
c. GCF of 72 and 16 = 8.
d. GCF of 10, 40, and 25 = 5.
Explanation:
In the above-given question,
given that,
Use any method to find the greatest common factor for the number pairs.
GCF = Greatest Common Factor.
a. GCF of 42 and 56 = 14.
factors of 42 = 1, 2, 3, 6, 7, 14, 21, and 42.
factors of 56 = 1, 2, 4, 7, 8, 14, 28, and 56.
so among those the greatest common factor is 14.
b. GCF of 32 and 80 = 16.
factors of 32 = 1, 2, 4, 8, 16, and 32.
factors of 80 = 1, 2, 4, 5, 8, 10, 16, 20, 40, and 80.
so among those the greatest common factor is 16.
c. GCF of 72 and 16 = 8.
factors of 72 = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
factors of 16 = 1, 2, 4, 8, and 16.
so among those the greatest common factor is 8.
d. GCF of 10, 40, and 25 = 5.
factors of 10 = 1, 2, 5, and 10.
factors of 40 = 1, 2, 4, 5, 8, 10, 20, and 40.
factors of 25 = 1, 5, and 25.
so among those the greatest common factor is 5.
Question 2.
Explain how you found GCF (42, 56) in Problem 1a.
Answer:
GCF of 42 and 56 = 14.
Explanation:
In the above-given question,
given that,
GCF = Greatest Common Factor.
GCF of 42 and 56 = 14.
factors of 42 = 1, 2, 3, 6, 7, 14, 21, and 42.
factors of 56 = 1, 2, 4, 7, 8, 14, 28, and 56.
so among those, the greatest common factor is 14.
Question 3.
Use the GCF to find an equivalent fraction for \(\frac{48}{64}\). Show your work.
Answer:
48/64 = 3/4.
Explanation:
In the above-given question,
given that,
use the GCF to find an equivalent fraction for 48/64.
48 = 6 x 8.
64 = 8 x 8.
6/8 = 3/4.
6 = 2 x 3.
8 = 2 x 4.
so 48/64 = 6/8.
Question 4.
Jenny will use 28 blue beads and 21 red beads to make identical bracelets.
a. What is the greatest number of bracelets she can make?
Answer:
The greatest number of bracelets she can make = 7.
Explanation:
In the above-given question,
given that,
Jenny will use 28 blue beads and 21 red beads to make identical bracelets.
factors of 28 = 1, 2, 4, 7, 14, and 28.
factors of 21 = 1, 3, 7, and 21.
so among those, the greatest common factor = 7.
b. How many blue beads and how many red beads will be on each bracelet?
Answer:
The number of blue beads and red beads will be on each bracelet = 7.
Explanation:
In the above-given question,
given that,
the number of blue beads = 4.
the number of red beads = 3.
4 + 3 = 7.
so the number of blue beads and red beads will be on each bracelet = 7.
Question 5.
Explain how a set of numbers can have a GCF greater than 1.
Answer:
Try This
Question 6.
GCF (12, 24, 30, 42) =
Answer:
GCF of 12, 24, 30, and 42= 6.
Explanation:
In the above-given question,
given that,
GCF of 12, 24, 30, and 42.
factors of 12 = 1, 2, 3, 4, 6, and 12.
factors of 24 = 1, 2, 3, 4, 6, 8, 12, and 24.
factors of 30 = 1, 2, 3, 5, 6, 10, 15, and 30.
factors of 42 = 1, 2, 3, 6, 7, 14, 21, and 42.
so among those, the greatest common factor = 6.
Practice
Insert the missing digits to make each number sentence true.
Question 7.
___, ____ 63 – 3,9 ___ 9 = 2,83 ___
Answer:
Question 8.
71, __ 4 ___ – 4,8 6 = 6 ___ ,270
Answer:
Everyday Mathematics Grade 6 Home Link 2.2 Answers
Least Common Multiple
Question 1.
Find the least common multiple for each pair of numbers.
a. LCM (10, 15) = ___
b. LCM (12, 15) = ___
c. LCM (6, 10) = ___
d. LCM (7, 5) = _____
Answer:
a. LCM of 10 and 15 = 30.
b. LCM of 12 and 15 = 60.
c. LCM of 6 and 10 = 30.
d. LCM of 7 and 5 = 35.
Explanation:
In the above-given question,
given that,
LCM of 10 and 15.
2 x 5 = 10.
3 x 5 = 15.
5 x 1 = 5.
2 x 3 x 5 = 30.
so LCM of 10 and 15 = 30.
LCM of 12 and 15.
12 = 3 x 4.
15 = 3 x 5.
3 x 4 x 5 = 60.
LCM of 6 and 10.
6 = 2 x 3.
10 = 2 x 5.
3 x 1 = 3.
5 = 5 x 1.
2 x 3 x 5 = 30.
LCM of 5 and 7.
5 x 7 = 35.
Question 2.
Find the greatest common factor and least common multiple for each pair of numbers.
a. GCF (75, 100) = ___
LCM (75, 100) =
Answer:
a. GCF of 75 and 100 = 25.
b. LCM of 75 and 100 = 300.
Explanation:
In the above-given question,
given that,
LCM of 75 and 100.
75 = 5 x 15.
100 = 5 x 20.
15 = 5 x 3.
20 = 5 x 4.
5 x 5 x 3 x 4 = 300.
GCF of 75 and 100.
75 = 3 x 5 x 5.
100 = 2 x 2 x 5 x 5.
5 x 5 = 25.
b. GCF (36, 48) = ___
LCM (36, 48) =
Answer:
a. GCF of 36 and 48 = 12.
b. LCM of 36 and 48 = 144.
Explanation:
In the above-given question,
given that,
LCM of 36 and 48.
36 = 2 x 2 x 3 x 3.
48 = 2 x 2 x 2 x 2 x 3.
2 x 3 x 2 x 2 x 2 = 144.
GCF of 36 and 48.
36 = 2 x 2 x 3 x 3.
48 = 2 x 2 x 2 x 2 x 3.
2 x 2 x 3 = 12.
Use the LCM to find equivalent fractions with the least common denominator.
Question 3.
\(\frac{3}{4}\) and \(\frac{5}{6}\)
LCM (4, 6) = ____
Fractions: ____
Answer:
LCM of 4 and 6 = 12.
Explanation:
In the above-given question,
given that,
LCM of 4 and 6.
4 = 2 x 2.
6 = 2 x 3.
2 x 2 x 3 = 12.
Question 4.
\(\frac{1}{6}\) and \(\frac{3}{8}\)
LCM (6, 8) = ___
Fractions: ____
Answer:
LCM of 6 and 8 = 24.
Explanation:
In the above-given question,
given that,
LCM of 6 and 8.
8 = 2 x 4.
6 = 2 x 3.
2 x 4 x 3 = 24.
Question 5.
\(\frac{4}{25}\) and \(\frac{4}{15}\)
LCM (25, 15) = ___
Fractions: ____
Answer:
LCM of 25 and 15 = 75.
Explanation:
In the above-given question,
given that,
LCM of 25 and 15.
25 = 5 x 5.
15 = 3 x 5.
5 x 5 x 3 = 75.
Question 6.
a. On a website, there is an ad for jeans every 5 minutes, an ad for sneakers every 10 minutes, and an ad for scarves every 45 minutes.
If they all appeared together at 9:00 P.M., when is the next time they will all appear together? _____
Answer:
The next time they will all appear together = 10:00 P.M.
Explanation:
In the above-given question,
given that,
On a website, there is an ad for jeans every 5 minutes, an ad for sneakers every 10 minutes, and an ad for scarves every 45 minutes.
5 + 10 = 15.
45 + 15 = 60 minutes.
60 minutes = 1 hour.
9:00 + 1 hour = 10: 00.
the next time they will all appear together = 10:00 p.m.
b. Explain how you used GCF or LCM to solve the problem.
Answer:
LCM of 5, 10, and 45 = 450.
GCF of 5, 10, and 45 = 5.
Explanation:
In the above-given question,
given that,
LCM of 5, 10, and 45.
5 = 5 x 1.
10 = 2 x 5.
45 = 3 x 15.
15 = 3 x 5.
2 x 3 x 3 x 5 x 5 = 450.
GCF of 5, 10, and 45.
5 = 1, 5.
10 = 5, 1, 10, and 2.
45 = 1, 45, 15, 3, 5, 9.
among all those, the greatest common factor is 5.
Question 7.
Explain why the LCM is at least as large as the GCF.
Answer:
LCM = Least common multiple.
GCF = greatest common factor.
Explanation:
In the above-given question,
given that,Aa
In LCM we will write the answer as the least common multiple.
In GCF we will write the answer as the greatest common factor.
Practice
Estimate.
Question 8.
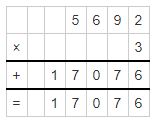
5,692 ∗ 3 = ____
Answer:
5692 x 3 = 17076.
Explanation:
In the above-given question,
given that,
5692 x 3.
Question 9.
69 ∗ 54 = ___
Answer:
69 x 54 = 3726.
Explanation:
In the above-given question,
given that,
69 x 54.

Question 10.
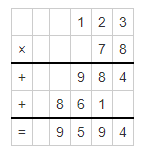
78 ∗ 123 = ___
Answer:
78 x 123 = 9594.
Explanation:
In the above-given question,
given that,
78 x 123.
Everyday Math Grade 6 Home Link 2.3 Answer Key
Fraction-Multiplication Review
Represent the problem on a number line, and then solve the problem.
Question 1.
\(\frac{2}{3}\)*\(\frac{9}{12}\) = ___

Answer:
2/3 x 9/12 = 0.42.
Explanation:
In the above-given question,
given that,
2/3 x 9/12.
2/3 = 0.6.
9/12 = 0.7.
0.6 x 0.7 = 0.42.
5/12 = 0.42.
2/3 x 9/12 = 5/12.
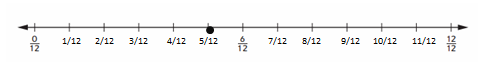
Question 2.
Maliah has \(\frac{2}{3}\) cup of raisins. She used \(\frac{1}{2}\) of her raisins to make muffins. What fraction of a cup of raisins did she use?

Number sentence: ____
Answer:
2/3 – 1/2 = 0.6.
Explanation:
In the above-given question,
given that,
Maliah has 2/3 cups of raisins.
she used 1/2 of her raisins to make muffins.
2/3 = 0.6.
0.3 + 0.3 = 0.6.
so Maliah use 0.6 cups of her raisins.
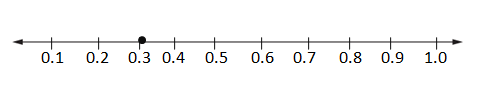
Question 3.
On the back of this page, write and solve a number story for \(\frac{1}{4}\) * \(\frac{1}{2}\).
Answer:
1/4 x 1/2 = 1/10.
Explanation:
In the above-given question,
given that,
1/4 x 1/2.
1/4 = 0.25.
1/2 = 0.5.
0.2 x 0.5 = 0.1.
Try This
Question 4.
Ryse sprinted \(\frac{3}{4}\) of a lap around the running track at school. A whole lap is \(\frac{1}{4}\) mile. How far did he sprint?
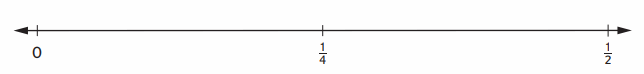
Number sentence: _______
Answer:
3/4 x 1/4 = 1/2.
Explanation:
In the above-given question,
given that,
Ryse sprinted 3/4 of a lap around the running track at school.
A whole lap is 1/4 mile.
3/4 x 1/4.
3/4 = 0.75.
1/4 = 0.25..
0.75 – 0.25 = 0.50.
1/2 = 0.5.
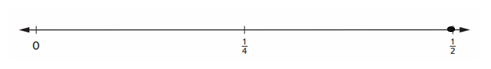
Practice
Estimate.
Question 5.
845 ÷ 24 = ___
Answer:
845 ÷ 24 = 35.
Explanation:
In the above-given question,
given that,
845 ÷ 24 = 35.
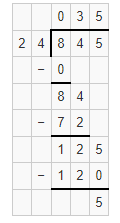
Question 6.
6,450 ÷ 639 = ___
Answer:
6450 ÷ 639 = 10.
Explanation:
In the above-given question,
given that,
6450 ÷ 639 = 10.

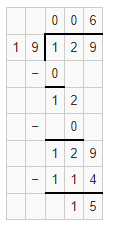
Question 7.
129 ÷ 19 = ___
Answer:
129 ÷ 19 = 10.
Explanation:
In the above-given question,
given that,
129 ÷ 19 = 10.
Everyday Mathematics Grade 6 Home Link 2.4 Answers
Companion Gardening
Draw and label area models and write number sentences to represent and solve Problems 1–2.
Question 1.
In companion planting, marigold flowers are used to repel insects that harm melon plants. Community gardeners plant \(\frac{2}{3}\) of a rectangular garden bed with melon plants. They plant \(\frac{3}{4}\) of the melon area with marigolds. What fraction of the garden bed will have both plants growing together? _____
Number sentence: _______
Answer:
Question 2.
Two plants that grow well together are tomatoes and basil. This year, \(\frac{1}{5}\) of a garden bed was planted with tomatoes and basil. Next year, the area will be 3 times as large. What will the area be next year? ____
Number sentence: ____
Answer:
First estimate, then use a partial-products diagram to solve Problem 3.
Question 3.
Last year a community garden produced 5\(\frac{1}{3}\) pounds of carrots. This year, better weather resulted in a harvest 2\(\frac{2}{3}\) times as large. How many pounds of carrots were harvested this year?
Estimate: ____
Number sentence: ___
Practice Find equivalent fractions.
Question 4.
\(\frac{3}{4}\) = 
Answer:
3/4 = 9/12.
Explanation:
In the above-given question,
given that,
equivalent fractions of 3/4.
3/4 = 3 x 3/4 x 3.
3 x 3 = 9.
4 x 3 = 12.
3/4 = 9/12.
Question 5.
\(\frac{18}{20}\) = 
Answer:
18/20 = 9/10.
Explanation:
In the above-given question,
given that,
equivalent fraction of 18/20.
18/20 = 9 x 2/10 x 2.
9 x 2 = 18.
10 x 2 = 20.
18/20 = 9/10.
Question 6.
\(\frac{6}{7}\) = 
Answer:
6/7 = 24/28.
Explanation:
In the above-given question,
given that,
equivalent fraction of 6/7.
6/7 = 6 x 4/7 x 4.
6 x 4 = 24.
7 x 4 = 28.
6/7 = 24/28.
Question 7.
\(\frac{24}{36}\) 
Answer:
24/36 = 2/3.
Explanation:
In the above-given question,
given that,
equivalent fraction of 24/36.
24/36 = 60/90.
6/9 = 4/6.
4/6 = 2/3.
24/26 = 2/3.
Everyday Math Grade 6 Home Link 2.5 Answer Key
Fraction Multiplication
Mara’s strategy: \(\frac{6}{8}\) ∗ \(\frac{2}{3}\) = (6 ∗ \(\frac{1}{8}\)) ∗ (2 ∗ \(\frac{1}{3}\))
= (6 ∗ 2) ∗ (\(\frac{1}{8}\) ∗ \(\frac{1}{3}\))
= 12 ∗ \(\frac{1}{24}\)
= \(\frac{12}{24}\)
Question 1.
Use Mara’s strategy to rename the fractions as whole numbers and unit fractions. Then group your factors to make the problem easier. Show the steps you use.
a. \(\frac{5}{2}\) ∗ \(\frac{2}{4}\)=
w
Answer:
\(\frac{10}{8}\).
Explanation:
In the above-given question,
given that,
Use Mara’s strategy to rename the fractions as whole numbers and unit fractions.
(5 ∗ \(\frac{1}{2}\)) ∗ (2 ∗ \(\frac{1}{4}\))
(5 ∗ 2) ∗ (\(\frac{1}{2}\) ∗ \(\frac{1}{4}\))
= 10 ∗ \(\frac{1}{8}\)
= \(\frac{10}{8}\)
b. \(\frac{10}{8}\) ∗ \(\frac{8}{10}\) =
Answer:
\(\frac{80}{80}\).
Explanation:
In the above-given question,
given that,
Use Mara’s strategy to rename the fractions as whole numbers and unit fractions.
(10 ∗ \(\frac{1}{8}\)) ∗ (8 ∗ \(\frac{1}{10}\))
(10 ∗ 8) ∗ (\(\frac{1}{8}\) ∗ \(\frac{1}{10}\))
= 80 ∗ \(\frac{1}{80}\)
= \(\frac{80}{80}\)
c. __ = 12 ∗ \(\frac{5}{6}\)
Answer:
\(\frac{60}{6}\).
Explanation:
In the above-given question,
given that,
Use Mara’s strategy to rename the fractions as whole numbers and unit fractions.
(12 ∗ \(\frac{5}{6}\)).
(12 ∗ 5) ∗ (\(\frac{1}{6}\).
= 60 ∗ \(\frac{1}{6}\)
= \(\frac{60}{6}\)
d. ___ = \(\frac{5}{2}\) ∗ 4
Answer:
\(\frac{20}{2}\).
Explanation:
In the above-given question,
given that,
Use Mara’s strategy to rename the fractions as whole numbers and unit fractions.
(4 ∗ \(\frac{5}{2}\)).
(4 ∗ 5) ∗ (\(\frac{1}{2}\).
= 20 ∗ \(\frac{1}{2}\)
= \(\frac{20}{2}\)
e. \(\frac{21}{3}\) ∗ \(\frac{6}{7}\) = ___
Answer:
\(\frac{126}{21}\).
Explanation:
In the above-given question,
given that,
Use Mara’s strategy to rename the fractions as whole numbers and unit fractions.
(21 ∗ \(\frac{1}{3}\)) ∗ (6 ∗ \(\frac{1}{7}\))
(21 ∗ 6) ∗ (\(\frac{1}{3}\) ∗ \(\frac{1}{7}\))
= 126 ∗ \(\frac{1}{21}\)
= \(\frac{126}{21}\)
f. 9 ∗ \(\frac{2}{9}\) = ___
Answer:
\(\frac{18}{9}\).
Explanation:
In the above-given question,
given that,
Use Mara’s strategy to rename the fractions as whole numbers and unit fractions.
(9 ∗ \(\frac{2}{9}\)).
(9 ∗ 2) ∗ (\(\frac{1}{9}\).
= 18 ∗ \(\frac{1}{9}\)
= \(\frac{18}{9}\)
Question 2.
Choose two problems from above that are alike in some way. Describe how they are alike.
Answer:
Use any model or strategy to solve Problems 3–4. Write a number sentence.
Question 3.
Samantha had 6 pages of homework. She finished \(\frac{2}{3}\) of her assignment. How many pages did she finish?
Number sentence:
_____________
Answer:
The number of pages did she finish = 5 pages.
Explanation:
In the above-given question,
given that,
Samantha had 6 pages of homework.
She finished 2/3 of her assignment.
2/3 = 0.6.
6 – 0.6 = 5.4.
so the number of pages did she finish = 5 pages.
Question 4.
A room measures 8\(\frac{1}{2}\) feet by 10\(\frac{2}{3}\)feet. What is the area of the room?
Number sentence:
________________
Answer:
\(\frac{160}{6}\).
Explanation:
In the above-given question,
given that,
(8 ∗ \(\frac{1}{2}\)) ∗ (10 ∗ \(\frac{2}{3}\))
(8 ∗ 10) ∗ (\(\frac{1}{2}\) ∗ \(\frac{2}{3}\))
= 80 ∗ \(\frac{2}{6}\)
= \(\frac{160}{6}\)
Practice
Question 5.
389 ∗ 17 = _________
Answer:
389 x 17 = 6613.
Explanation:
In the above-given question,
given that,
389 x 17.
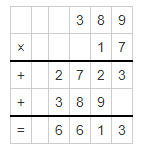
Question 6.
____ = 176 ∗ 48
Answer:
176 x 48 = 8448.
Explanation:
In the above-given question,
given that,
176 x 48.
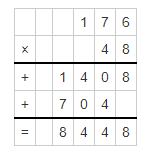
Question 7.
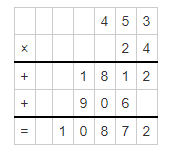
453 ∗ 24 = ____
Answer:
453 x 24 = 10872.
Explanation:
In the above-given question,
given that,
453 x 24.
Everyday Mathematics Grade 6 Home Link 2.6 Answers
Division Using Home Link 2-6 Common Denominators
Question 1.
Draw a picture or diagram and solve the problem. Rudi has 4 cups of almonds. His trail mix recipe calls for \(\frac{2}{3}\) cup of almonds. How many batches of trail mix can he make?
Answer:
Question 2.
Use common denominators to solve the problems.
Write a number sentence to show how you rewrote the problem with common denominators.
Check your answers.
a. \(\frac{3}{4}\) ÷ \(\frac{3}{8}\) = _______ Number sentence: _________
Answer:
3/4 ÷ 3/8 = 2.
Explanation:
In the above-given question,
given that,
Use common denominators to solve the problems.
3/4 = 0.75.
3/8 = 0.3.
0.75/0.375 = 2.
b. 3\(\frac{1}{3}\) ÷ \(\frac{5}{6}\) = ___ Number sentence: ____
Answer:
3(1/3) ÷ 5/6 = 4.
Explanation:
In the above-given question,
given that,
Use common denominators to solve the problems.
3 x 3 = 9.
9 + 1 = 10.
10/3 = 3.3.
5/6 = 0.8.
3.3/0.8 = 4.1.
c. \(\frac{36}{8}\) ÷ \(\frac{1}{2}\) = ___ Number sentence: _______
Answer:
36/8 ÷ 1/2 = 9.
Explanation:
In the above-given question,
given that,
Use common denominators to solve the problems.
36/8 = 4.5.
1/2 = 0.5.
4.5/0.5 = 9.
Question 3.
Michelle is cutting string to make necklaces. She has 15 feet of string. She needs 1\(\frac{1}{2}\) feet of string for each necklace.
How many necklaces can she make? Number model: ______ Solution: _________
Answer:
The number of necklaces she can make = 10.
Explanation:
In the above-given question,
given that,
Michelle is cutting string to make necklaces.
She has 15 feet of string.
she needs 3/2 feet of string for each necklace.
3/2 = 1.5.
1.5 x 10 = 15.
so she can make 10 necklaces.
Question 4.
A rectangular window has an area of 4\(\frac{1}{2}\) square meters. Its width is \(\frac{3}{4}\) meter. What is its length?
Number model: ____ Solution: ___
Answer:
The length of the rectangular window = 6 m.
Explanation:
In the above-given question,
given that,
A rectangular window has an area of 4 x 1/2 sq m.
4 x 2 = 8.
8 + 1 = 9.
9/2 = 4.5.
width = 3/4.
3/4 = 0.75.
area = l x w.
4.5 = l x 0.75.
l = 4.5/0.75.
length = 6.
so the length of the rectangular window = 6 meters.
Practice
Solve.
Question 5.
GCF (20, 30) = ___
Answer:
GCF of 20 and 30 = 10.
Explanation:
In the above-given question,
given that,
GCF of 2 and 30.
GCF = greatest common factor.
factors of 20 = 1, 2, 4, 5, 10, and 20.
factors of 30 = 1, 2, 3, 5, 6, 10, 15, and 30.
among all those 10 is the common factor.
Question 6.
GCF (6, 16) = ___
Answer:
GCF of 6 and 16 = 2.
Explanation:
In the above-given question,
given that,
GCF of 6 and 16.
GCF = greatest common factor.
factors of 6 = 1, 2, and 3.
factors of 16 = 1, 2, 4, and 8.
among all those 2 is the common factor.
Question 7.
GCF (36, 54) = __
Answer:
GCF of 36 and 54 = 2.
Explanation:
In the above-given question,
given that,
GCF of 36 and 54.
GCF = greatest common factor.
factors of 36 = 1, 2, and 3.
factors of 54 = 1, 2, 4, and 8.
among all those 2 is the common factor.
Everyday Math Grade 6 Home Link 2.7 Answer Key
More Exploring Fraction Division
For problems 1–3, circle the best estimate and the correct number model. Then solve the problem.
Question 1.
Stan is in wood working class with 6 friends. They have to split a board that is 4\(\frac{2}{3}\) feet long equally among the seven of them. How long will each person’s piece be?
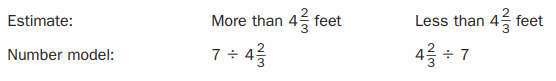
Answer: ____
The long will each person’s piece be = 4.6 feet.
Explanation:
In the above-given question,
given that,
Stan is in woodworking class with 6 friends.
They have to split a board that is 4\(\frac{2}{3}\) feet long equally among the seven of them.
4(2/3) = 3 x 4 = 12.
12 + 2 = 14.
14/3 = 4.6.
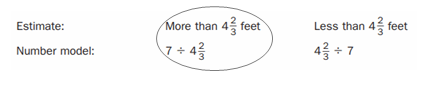
Question 2.
The area of a rectangle is 10\(\frac{1}{2}\) square feet. The length is 5\(\frac{1}{4}\) feet. How wide is the rectangle?
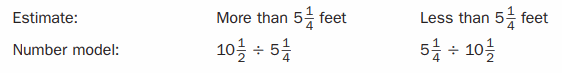
Answer: ____
The width of the rectangle = 2 ft.
Explanation:
In the above-given question,
given that,
the area of a rectangle is 10(1/2) sq ft.
length = 5 (1/4) ft.
10 x 2 = 20.
20 + 1 = 21.
21/2 = 10.5.
5 x 4 = 20.
20 + 1 = 21.
21/4 = 5.25.
area = l x w.
10.5 = 5.25 x w.
w = 10.5/5.25.
w = 2 ft.
so the width of the rectangle = 2 ft.
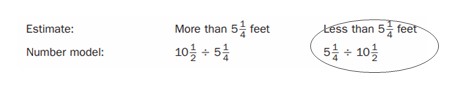
Question 3.
Sounya walks dogs on Saturdays. It takes \(\frac{3}{4}\) of an hour to walk each dog. She has 5\(\frac{1}{4}\) hours. How many dogs can she walk?
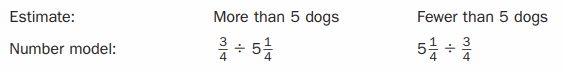
Answer: ___
The number of dogs she can walk = more than 5 dogs.
Explanation:
In the above-given question,
given that,
Sounya walks dogs on Saturdays.
It takes 3/4 of an hour to walk each dog.
she has 5(1/4) hours.
3/4 = 0.75.
5(1/4) = 5 x 4 = 20.
20 + 1 = 21.
21/4 = 5.25.
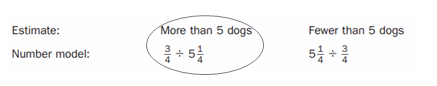
Practice
Find the LCM.
Question 4.
LCM (3, 7) = ___
Answer:
LCM of 3 and 7 = 21.
Explanation:
In the above-given question,
given that,
LCM of 3 and 7.
LCM = least common multiple.
3 = 3 x 1.
7 = 7 x 1.
3 x 7 = 21.
Question 5.
LCM (8, 4) = __
Answer:
LCM of 8 and 4 = 8.
Explanation:
In the above-given question,
given that,
LCM of 8 and 4.
LCM = least common multiple.
4 = 2 x 2.
2 = 2 x 1.
8 = 2 x 4.
4 = 2 x 2.
2 = 2 x 1.
2 x 2 x 2 = 8.
Question 6.
LCM (10, 4) = ___
Answer:
LCM of 10 and 4 = 20.
Explanation:
In the above-given question,
given that,
LCM of 10 and 4.
LCM = least common multiple.
10 = 2 x 5.
4 = 2 x 2
5 = 5 x 1.
2 x 2 x 5 = 20.
Everyday Mathematics Grade 6 Home Link 2.8 Answers
Fraction Division
Rewrite and solve the division problems using the Division of Fractions Property.
Example: \(\frac{3}{8}\) ÷ \(\frac{2}{5}\) = \(\frac{3}{8}\) ∗ \(\frac{5}{2}\) = \(\frac{15}{16}\)
Question 1.
3 ÷ \(\frac{2}{3}\) = ___
Answer:
3 ÷ 2/3 = 9/2.
Explanation:
In the above-given question,
given that,
3 ÷ 2/3.
3 ÷ 3/2.
9/2.
Question 2.
\(\frac{1}{5}\) ÷ \(\frac{8}{9}\) = ___
Answer:
\(\frac{9}{40}\).
Explanation:
In the above-given question,
given that,
\(\frac{1}{5}\) ÷ \(\frac{8}{9}\)
\(\frac{1}{5}\) ∗ \(\frac{8}{9}\).
\(\frac{1}{5}\) ∗ \(\frac{9}{8}\).
\(\frac{9}{40}\)
Question 3.
4 ÷ \(\frac{5}{7}\) = ___
Answer:
\(\frac{28}{5}\)
Explanation:
In the above-given question,
given that,
4 ÷ \(\frac{5}{7}\)
4 ∗ \(\frac{5}{7}\).
4 ∗ \(\frac{7}{5}\).
\(\frac{28}{5}\)
Question 4.
1\(\frac{2}{3}\) ÷ \(\frac{3}{5}\) = ______
Answer:
\(\frac{25}{9}\)
Explanation:
In the above-given question,
given that,
1\(\frac{2}{3}\) ÷ \(\frac{3}{5}\)
\(\frac{5}{3}\) ∗ \(\frac{3}{5}\).
\(\frac{5}{3}\) ∗ \(\frac{5}{3}\).
\(\frac{25}{9}\)
Question 5.
\(\frac{2}{5}\) ÷ \(\frac{3}{4}\) = ____
Answer:
\(\frac{8}{15}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{5}\) ÷ \(\frac{3}{4}\)
\(\frac{2}{5}\) ∗ \(\frac{3}{4}\).
\(\frac{2}{5}\) ∗ \(\frac{4}{3}\).
\(\frac{8}{15}\)
Question 6.
\(\frac{3}{5}\) ÷ 4 = ____
Answer:
\(\frac{20}{3}\)Explanation:
In the above-given question,
given that,
4 ÷ \(\frac{3}{5}\)
4 ∗ \(\frac{3}{5}\).
4 ∗ \(\frac{5}{3}\).
\(\frac{20}{3}\)
Question 7.
How many \(\frac{1}{4}\)-cup servings of cottage cheese are in a 3-cup container?
Division number model: ______ Multiplication number model: _______
Solution: _________
Answer:
\(\frac{12}{1}\)
Explanation:
In the above-given question,
given that,
3 ÷ \(\frac{1}{4}\)
3 ∗ \(\frac{1}{4}\).
3 ∗ \(\frac{4}{1}\).
\(\frac{12}{1}\)
Question 8.
Philip went on a 3\(\frac{1}{2}\)-mile hike. He hiked for 2 hours.
About how far did he go in 1 hour?
Division number model: ____ Multiplication number model: ______
Solution: _________
Answer:
Question 9.
Adam is using ribbon to decorate name tags for the class picnic.
He has 8\(\frac{2}{3}\) feet of blue ribbon. He needs \(\frac{1}{3}\) foot of ribbon for each name tag. How many name tags can he decorate?
Division number model: ______ Multiplication number model: ________
Solution: _______
Answer:
The number of name tags he can decorate = 28.
Explanation:
In the above-given question,
given that,
Adam is using ribbon to decorate name tags for the class picnic.
he as 8(2/3) feet of blue ribbon.
8 x 3 = 24.
24 + 2 = 26.
26/3 = 8.6.
1/3 = 0.3.
0.3 x 28 = 8.6.
so the number of name tags he can decorate = 28.
Practice
Add or subtract.
Question 10.
$4.50 + $3 = ___
Answer:
$4.50 + $3 = $7.5.
Explanation:
In the above-given question,
given that,
Add or Subtract.
$4.50 + $3.
$7.5.
Question 11.
$5.00 – $3.20 = ___
Answer:
$5 – $3.2 = $1.8.
Explanation:
In the above-given question,
given that,
Add or Subtract.
$5 – $3.2.
$1.8.
Question 12.
___ = $6.30 + $0.45 + $1.35
Answer:
$6.30 + $0.45 + $1.35 = $8.1
Explanation:
In the above-given question,
given that,
$6.30 + $0.45 + $1.35.
$6.30 + $0.45 = $6.75.
$6.75 + $1.35 = $8.1.
Everyday Math Grade 6 Home Link 2.9 Answer Key
Using Ratios to Represent Situations
Question 1.
Lenore’s dog gave birth to a litter of 9 puppies.
Two of the puppies are male. Write ratios for the following:
Number of female puppies to the total number of puppies ___________
Number of male puppies to female puppies ________
Answer:
The number of female puppies to the total number of puppies = 7: 9.
The number of male puppies to the total number of puppies = 2: 9.
Explanation:
In the above-given question,
given that,
Lenore’s dog gave birth to a litter of 9 puppies.
Two of the puppies are male.
The number of female puppies to the total number of puppies = 7: 9.
The number of male puppies to the total number of puppies = 2: 9.
For Problems 2–4, draw a picture to help you solve the problem. Record a ratio.
Question 2.
There are 15 tiles. 2 out of 5 tiles are white. How many tiles are white? ____ Write the ratio of white tiles to total tiles.
Answer:
The ratio of white tiles to total tiles = 5:15.
Explanation:
In the above-given question,
given that,
There are 15 tiles.
2 out of 5 tiles are white.
5:15.
so the ratio of white tiles to the total tiles = 5;15.
Question 3.
There are 24 tiles. 3 out of 4 tiles are white. How many tiles are white? ___ Write the ratio of white tiles to shaded tiles.
Answer:
The ratio of white tile to shaded tiles = 3:20.
Explanation:
In the above-given question,
given that,
There are 24 tiles.
3 out of 4 tiles are white.
3: 20.
so the ratio of white tiles to shaded tiles = 3:20.
Question 4.
There are 3 times as many white tiles as there are shaded tiles. Write this ratio. How many tiles are white if there are 12 tiles in total?
Answer:
The number of tiles are white = 9.
Explanation:
In the above-given question,
given that,
There are 3 times as many white tiles as there are shaded tiles.
3 x 3 = 9.
so the number of tiles are white = 9.
Question 5.
The Mighty Marble Company fills bags of marbles with a ratio of 3 Special Swirls out of every 9 marbles. How many Special Swirls are in a bag that has 21 marbles? ____
Answer:
The number of Special Swirls are in a bag that has 21 marbles = 7.
Explanation:
In the above-given question,
given that,
The Mighty marble Company fills bags of marbles with a ratio of 3 special swirls out of every 9 marbles.
3 x 3 = 9.
6 x 3 = 18.
7 x 3 = 21.
so the number of special swirls are in a bag that has 21 marbles = 7.
Try This
Question 6.
One class of 28 students has a ratio of 3 girls to 4 boys. What is the ratio for the number of boys to total number of students in the class?
______________
There are 60 girls in the whole sixth grade and the ratio is the same. How many students are there in sixth grade?
Answer:
The total number of boys to the total number of students = 7:28.
Explanation:
In the above-given question,
given that,
One class of 28 students has a ratio of 3 girls to 4 boys.
7 x 4 = 28.
7: 28.
so the total number of boys to the total number of students = 7:28.
Practice Solve.
Question 7.
\(\frac{5}{6}\) ∗ \(\frac{3}{4}\) = ___
Answer:
5/6 x 3/4 = 0.6225.
Explanation:
In the above-given question,
given that,
5/6 x 3/4.
5/6 = 0.8.
3/4 = 0.75.
0.83 x 0.75 = 0.6225.
Question 8.
\(\frac{2}{3}\) ∗ 1\(\frac{1}{2}\) = ___
Answer:
2/3 x 3/2 = 0.9.
Explanation:
In the above-given question,
given that,
2/3 x 1(1/2).
2 x 1 = 2.
2 + 1 = 3.
3/2 = 1.5.
2/3 = 0.6.
2/3 x 3/2 = 0.9.
Question 9.
\(\frac{8}{9}\) ∗ \(\frac{2}{7}\) =
Answer:
8/9 x 2/7 = 0.16.
Explanation:
In the above-given question,
given that,
8/9 x 2/7.
8/9 = 0.8.
2/7 = 0.2.
8/9 x 2/7 = 0.16.
Everyday Mathematics Grade 6 Home Link 2.10 Answers
More with Tape Diagrams
Draw tape diagrams to solve the problems. Label your diagrams and your answers.
Frances is helping her father tile their bathroom floor. They have tiles in two colors: green and white. They want a ratio of 2 green tiles to 5 white tiles.
a. They use 30 white tiles. How many green tiles do they use?
______________
Answer:
b. How many white tiles would they need if they use 16 green tiles?
Answer:
c. They use 35 tiles in all. How many are green?
Answer:
d. They use 49 tiles. How many of each color did they use?
Answer:
e. Explain how you used the tape diagram to solve Part d.
Answer:
Try This
Question 2.
Frances and her father decide to also tile their kitchen floor. For every 3 white tiles they plan to use 7 green tiles. The kitchen floor has room for 63 tiles total. Explain why they cannot cover the kitchen floor using the ratio 3 : 7.
Answer:
Yes, they cannot cover the kitchen floor using 3:7.
Explanation:
In the above-given question,
given that,
Frances and her father decide to also tile their kitchen floor.
For every 3 white tiles, they plan to use 7 green tiles.
but they used to keep for every 9 white tiles they plan to use 7 green tiles.
7 x 9 = 63.
Practice Divide.
Question 3.
\(\frac{4}{5}\) ÷ \(\frac{1}{5}\) = ____
Answer:
4/5 ÷ 1/5 = 4.
Explanation:
In the above-given question,
given that,
4/5 = 0.8.
1/5 = 0.2.
0.8/0.2 = 4.
4/5 ÷ 1/5 = 4.
Question 4.
\(\frac{1}{5}\) ÷ \(\frac{4}{5}\) = ____
Answer:
1/5 ÷ 4/5 = 1/4.
Explanation:
In the above-given question,
given that,
4/5 = 0.8.
1/5 = 0.2.
0.2/0.8 = 0.25.
1/5 ÷ 4/5 = 1/4.
Question 5.
7 ÷ \(\frac{1}{2}\) = _____
Answer:
7 ÷ 1/2 = 14.
Explanation:
In the above-given question,
given that,
1/2 = 0.5.
7 ÷ 0.5 = 14.
Everyday Mathematics Grade 6 Home Link 2.11 Answers
Finding Equivalent Ratios
Use the pictures to help you figure out the equivalent ratios
Question 1.

Answer:
1 foot = 12 inches.
3 feet = 36 inches.
7 feet = 84 inches.
144 inches = 12 feet.
Explanation:
In the above-given question,
given that,
the ratio of the foot to inches.
1 foot = 12 inches.
3 feet = 36 inches.
3 x 12 = 36.
7 feet = 84 inches.
7 x 12 = 84.
12 feet = 144 inches.
12 x 12 = 144.

Question 2.

Answer:
10 mm = 1 cm.
50 mm = 5 cm.
3000 mm = 300 cm.
250 mm = 25 cm.
Explanation:
In the above-given question,
given that,
the ratio of the mm to cm.
10 mm = 1 cm.
50 mm = 5 cm.
5 x 10 = 50 mm.
3000 mm = 300 cm.
300 x 10 = 3000.
250 mm = 25 cm.
25 x 10 = 250.

Question 3.

Answer:
8 legs = 1 spider.
Explanation:
In the above-given question,
given that,
the ratio of the legs to the spider.
8 legs are there in the figure.
8 legs = 1 spider.

Question 4.
a. Circle the similar rectangles.
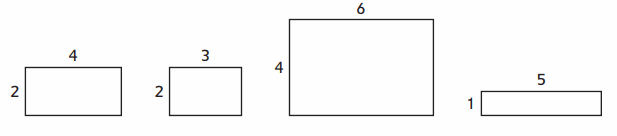
Answer:
The rectangles are not similar.
Explanation:
In the above-given question,
given that,
circle the similar rectangles.
the area of the rectangle = l x b.
where l = length and b = breadth.
the area of A = 4 x 2.
4 x 2 = 8.
rectangle B = 3 x 2
3 x 2 = 6.
rectangle C = 6 x 4.
6 x 4 = 24.
rectangle D = 5 x 1.
5 x 1 = 5.
b. Explain why the rectangles you circled are similar.
Answer:
The rectangles are not similar.
Explanation:
In the above-given question,
given that,
rectangle A = 4 x 2.
4 x 2 = 8.
rectangle B = 3 x 2
3 x 2 = 6.
rectangle C = 6 x 4.
6 x 4 = 24.
rectangle D = 5 x 1.
5 x 1 = 5.
so the rectangles are not similar.
c. Under each rectangle, use fraction notation to write the width-to-height ratio.
Answer:
Rectangle A = 4 : 2.
Rectangle B = 3 : 2.
Rectangle C = 6 : 4.
Rectangle D = 5 : 1.
Explanation:
In the above-given question,
given that,
rectangle A = 4 x 2.
4 x 2 = 8.
rectangle B = 3 x 2
3 x 2 = 6.
rectangle C = 6 x 4.
6 x 4 = 24.
rectangle D = 5 x 1.
5 x 1 = 5.
Practice Multiply mentally to find the cost.
Question 5.
4 pens at $2.98 each ___
Answer:
4 x $2.98 = 11.92.
Explanation:
In the above-given question,
given that,
4 pens at $2.98 each.
4 x $2.98.
11.92.
Question 6.
3 books at $24.95 each ____
Answer:
3 x $24.95 = $74.85.
Explanation:
In the above-given question,
given that,
3 books at $24.95 each.
3 x $24.95.
$74.85.
Everyday Math Grade 6 Home Link 2.12 Answer Key
Using Ratios to Make Fruit Cups
Oliver has two fruit-cup recipes that have different ratios of raspberries and watermelon.

Question 1.
a. Which fruit-cup recipe would have a stronger raspberry taste? ______
Answer:
Recipe A has a stronger raspberry taste.
Explanation:
In the above-given question,
given that,
Oliver has two fruit-cup recipes that have different ratios of raspberries and watermelon.
Recipe A has 2 cups raspberries and 3 cups watermelon.
Recipe B has 5 cups raspberries 11 cups total.
so Recipe A has a stronger raspberry taste.
b. Draw a picture or diagram to support your answer.
Answer:
c. Explain how your picture or diagram supports your answer.
Answer:
Question 2.
Create a fruit-cup recipe that would taste the same as Recipe B, but uses more than 11 cups of fruit.
List your ingredients: ______
Answer:
The ingredients are bananas and grapes.
Explanation:
In the above-given question,
given that,
create a fruit-cup recipe that would taste the same as Recipe B, but uses more than 11 cups of fruit.
the 8 cups of bananas and 4 cups of grapes.
Question 3.
Create a fruit-cup recipe that would make a fruit cup with a weaker raspberry taste than Recipes A and B.
List your ingredients: _______
Answer:
The ingredients are bananas and grapes.
Explanation:
In the above-given question,
given that,
create a fruit-cup recipe that would make a fruit cup with a weaker raspberry taste than recipes A and B.
the 8 cups of bananas and 3 cups of grapes.
Try This
Question 4.
If you only want 1 cup of fruit salad made from Recipe A, what measurements of watermelon and raspberries do you need?
Answer:
Practice Divide.
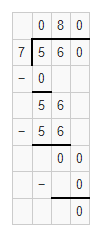
Question 5.
560 ÷ 7 = ____
Answer:
560 ÷ 7 = 80.
Explanation:
In the above-given question,
given that,
560 / 8.
Question 6.
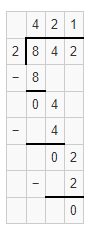
842 ÷ 2 = ____
Answer:
842 ÷ 2 = 421.
Explanation:
In the above-given question,
given that,
842 / 2.
Question 7.
930 ÷ 3 = ____
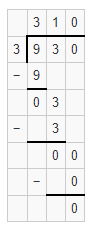
Answer:
930 ÷ 3 = 310.
Explanation:
In the above-given question,
given that,
930 / 3.
Everyday Math Grade 6 Home Link 2.13 Answer Key
Ratio/Rate Tables and Unit Rates
Question 1.
List three examples of a rate:
____________
Draw a ratio/rate table to solve each problem. The first table has been drawn for you, but it is not complete.
Answer:
Question 2.
One 12-ounce can of frozen juice is mixed with three 12-ounce cans of water. How many cans of water do you need for 4 cans of juice?
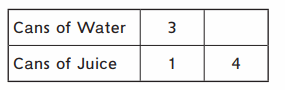
_____________
Answer:
The number of cans of water need for 4 cans of juice = 12 cans.
Explanation:
In the above-given question,
given that,
One 12-ounce can of frozen juice is mixed with three 12-ounce cans of water.
1 x 3 = 3.
4 x 3 = 12.
so the 4 cans of juice are mixed with 12 cans of water.
Question 3.
A hiker’s map has a scale of 3 inches to 10 miles. The trail is 4 inches long on the map. How long is the actual hike? ______
Answer:
Question 4.
Amy types 125 words in 2 minutes. About how long will it take her to type a 1,500-word report? ____
Answer:
Amy types a 1,500-word report in 24 minutes.
Explanation:
In the above-given question,
given that,
Amy types 125 words in 2 minutes.
125 + 125 = 250.
250 x 6 = 1500.
Amy types a 1,500-word report in 24 minutes.
Try This
Question 5.
A recipe for lime salad dressing calls for \(\frac{1}{4}\) cup lime juice and \(\frac{3}{4}\) cup olive oil. How much lime juice would you use with 1 cup olive oil? _______
Answer:
Practice Record >, <, or =.
Question 6.
-3 ___ -5
Answer:
-3 > -5.
Explanation:
In the above-given question,
given that,
-3 and -5.
-3 is greater than -5.
-3 > -5.
Question 7.
6 ____ -7
Answer:
6 > -7.
Explanation:
In the above-given question,
given that,
6 and -7.
6 is greater than -7.
6 > -7.
Question 8.
-8 ____ -9
Answer:
-8 > -9.
Explanation:
In the above-given question,
given that,
-8 and -9.
-8 is greater than -9.
-8 > -9.
Everyday Math Grade 6 Home Link 2.14 Answer Key
Graphing Rates
Snails move slowly. Jada, Reality, and Barb had a snail race. Then they compared the rates at which the snails crawled.
Question 1.
Fill in the ratio/rate table with equivalent rates.
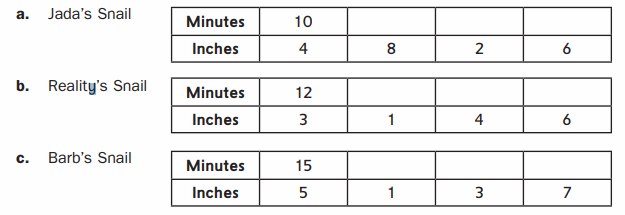
Answer:
Question 2.
Treat each rate as an ordered pair. Graph each snail’s rate using a different color.
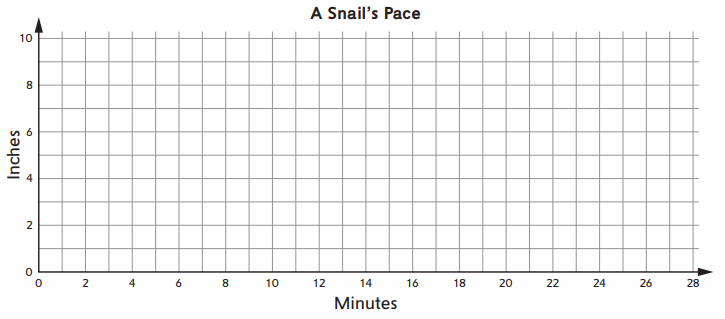
Answer:
Question 3.
Which snail is the fastest? Use the graph to explain how you know
Answer:
Practice Insert >, <, or = to make each sentence true.
Question 4.
7 ___ 4.65
Answer:
7 > 4.65.
Explanation:
In the above-given question,
given that,
7 and 4.65.
7 is greater than 4.65.
4.65 = 5.
7 > 4.65.
Question 5.
0.1 __ 0.01
Answer:
0.1 > 0.01.
Explanation:
In the above-given question,
given that,
0.1 and 0.01.
0.1 is greater than 0.01.
0.1 > 0.01.
Question 6.
0.205 ___ 0.22
Answer:
0.205 < 0.22.
Explanation:
In the above-given question,
given that,
0.205 and 0.22.
0.205 is less than 0.22.
0.205 < 0.22.