Everyday Math Grade 5 Answers Unit 8 Applications of Measurement, Computation, and Graphing

Everyday Mathematics 5th Grade Answer Key Unit 8 Applications of Measurement, Computation, and Graphing

Everyday Mathematics Grade 5 Home Link 8.1 Answers

Comparing Yard Sizes

Question 1.
Some neighbors are deciding where to hold the annual cookout and block party. They would like to have it in the largest backyard. Use the dimensions given to find the area of each neighbor’s backyard in square feet and square yards. Then answer the questions.

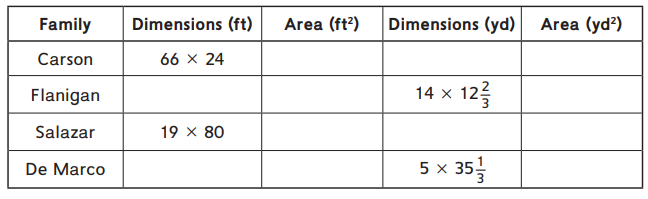
Answer:
Carson: area = 1584 sq ft, Dimensions = 22 x 8 yds, area in sq yds = 176.
Flanigan: Dimensions in feet = 42 x 38 ft, Area in sq ft = 1596, Area in sq yds = 177(1/3).
Salazar: Area in sq ft = 1520, Dimensions = 6(1/3) x 26(2/3), Area in sq yds = 168(8/9).
De Marco: Dimensions in feet = 15 x 106 ft, Area in sq ft = 1590, Area in sq yds = 176(2/3).

Explanation:
In the above-given question,
given that,
Families neighbor’s backyard in square feet and square yards.
area = l x w.
where l = length, and w = width.
area = 66 x 24.
area = 1584.
1 feet = 0.333 yds.
66 x 0.333 = 21.978.
21.978 = 22.
24 x 8 = 7.992.
7.992 = 8 yds.
area = 22 x 8 = 176.
Flanigan: Dimensions in feet = 42 x 38 ft, Area in sq ft = 1596, Area in sq yds = 177(1/3).
Salazar: Area in sq ft = 1520, Dimensions = 6(1/3) x 26(2/3), Area in sq yds = 168(8/9).
De Marco: Dimensions in feet = 15 x 106 ft, Area in sq ft = 1590, Area in sq yds = 176(2/3).

Question 2.
a. Which family has the largest yard?
b. Which family has the smallest yard?

Answer:
a. Flanigan family has the largest yard.
b. Salazar family has the smallest yard.

Explanation:
In the above-given question,
given that,
a. Flanigan dimensions = 14 x 12(2/3).
area = l x w.
where l = 14.
w = 38/3.
area = 14 x 12(2/3).
area = 177(1/3) sq yds.
b. Salazar dimensions = 19 x 80.
area = l x b.
where l = 19.
b = 80.
area = 1520.

Question 3.
Look at the number of square feet and the number of square yards in each family’s yard. What number could you multiply the number of square yards by to get the number of square feet? Explain why this makes sense.

Answer:
9.

Explanation:
In the above-given question,
given that,
There are 9 square feet in 1 square yard.
so it makes sense that an area in square feet would be 9 times the area in square yards.

Practice
Question 4.
$\frac{3}{4}$ ∗ 7 = ______

Answer:
$\frac{3}{4}$ ∗ 7 = 21/4.

Explanation:
In the above-given question,
given that,
multiply.
$\frac{3}{4}$ ∗ 7.
3/4 x 7.
7 x 3/4 = 21/4.
$\frac{3}{4}$ ∗ 7 = 21/4.

Question 5.
17 ∗ $\frac{2}{5}$ = ________

Answer:
17 ∗ $\frac{2}{5}$ = 34/5.

Explanation:
In the above-given question,
given that,
multiply.
$\frac{2}{5}$ ∗ 17.
2/5 x 17.
17 x 2/5 = 34/5.
$\frac{2}{5}$ ∗ 17 = 34/5.

Question 6.
9 ∗ $\frac{11}{12}$ = ______

Answer:
9 ∗ $\frac{11}{12}$ = 99/12.

Explanation:
In the above-given question,
given that,
multiply.
$\frac{11}{12}$ ∗ 9.
11/12 x 9.
9 x 11/12 = 99/12.
$\frac{11}{12}$ ∗ 9 = 99/12.

Question 7.
$\frac{15}{16}$ ∗ 5 = _________

Answer:
$\frac{15}{16}$ ∗ 5 = 75/16.

Explanation:
In the above-given question,
given that,
multiply.
$\frac{15}{16}$ ∗ 5.
15/16 x 5.
5 x 15/16 = 75/16.
$\frac{15}{16}$ ∗ 5 = 75/16.

Everyday Math Grade 5 Home Link 8.2 Answer Key

Finding Area with the Rectangle Method

Use the rectangle method to find the area of each figure. To use the rectangle method:

Draw one or more rectangles around the figure or parts of the figure.
Use the area of the rectangle(s) to determine the area of the original figure.

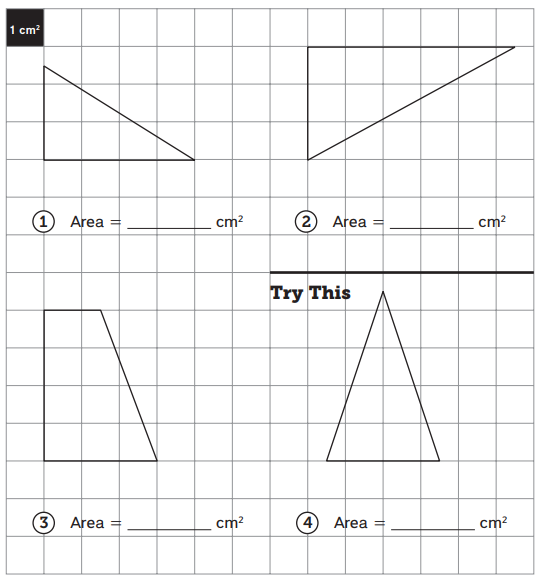
$Everyday Math Grade 5 Home Link 8.2 Answer Key 1$

Answer:
1: 5, 2: 8(1/4), 3: 9, 4: 6(3/4).

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
where b = base and h = height.
1.area = 1/2 x 5 x 2.5.
area = 5.
where 2 and 2.5 get canceled.
2.area = 1/2 x 5.5 x 3.
area = 5.5 x 3/2.
area = 8(1/4).
3.area = 1/2 x 3 x 4.
area = 12/2.
area = 6.

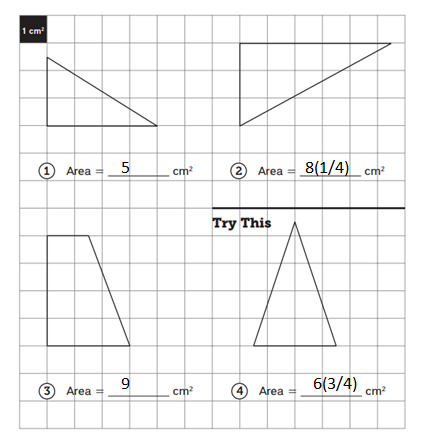
Practice
Solve. Show your work on the back of this page.
Question 5.
0.14 ∗ 8 = ______

Answer:
0.14 x 8 = 1.12.

Explanation:
In the above-given question,
given that,
multiply.
0.14 x 8.
1.12.

Question 6.
2.75 ∗ 4.3 = ________

Answer:
2.75 x 4.3 = 11.825.

Explanation:
In the above-given question,
given that,
multiply.
2.75 x 4.3.
11.825.

Everyday Mathematics Grade 5 Home Link 8.3 Answers

Solving Remodeling Problems

Therese is remodeling her bedroom. A drawing of her bedroom is shown below. Solve Therese’s remodeling problems. Show your work.
Question 1.
How many square feet of carpet should Therese buy to cover the entire floor of her room? ________ ft²

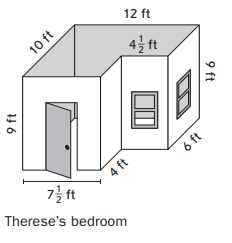
Answer:
The Therese buy to cover the entire floor of her room = 102 sq ft.

Explanation:
In the above-given question,
given that,
area of the rectangle 1 = b x h.
where b = base, h = height.
area = 7(1/2) x 9.
area = 63/2.
area of the rectangle 2 = b x h.
area = 4 x 9.
area = 36.
area of the rectangle 3 = b x h.
area = 6 x 9.
area = 54.
the total area of all the rectangles = areas of rectangle 1+ 2 + 3.
63 + 36 + 54.
90 + 12 = 102 sq ft.
so therese buy to cover the entire floor of her room = 102 sq ft.

Question 2.
Which air conditioner should Therese buy for her room?
The Coolmax: Cools up to 800 cubic feet
The Ice Storm: Cools up to 1,500 cubic feet
The Polar Extreme: Cools up to 2,500 cubic feet
Explain your choice.

Answer:
The Ice Storm should Therese buy for her room.

Explanation:
In the above-given question,
given that,
CoolMax cools up to 800 cubic feet.
Ice storm cools up to 1500 cubic feet.
Polar Extreme cools up to 2500 cubic feet.
so Therese buys medium temperature.

Practice
Solve. Show your work on the back of this page.
Question 3.
4 $\frac{3}{4}$ ∗ $\frac{1}{2}$ = __________

Answer:
4 $\frac{3}{4}$ ∗ $\frac{1}{2}$ = 19/8.

Explanation:
In the above-given question,
given that,
4 x 3/4 = 4 x 4.
4 x 4 = 16.
16 + 3/4 x 1/2.
4 x 2 = 8.
19/8.
4 $\frac{3}{4}$ ∗ $\frac{1}{2}$ = 19/8.

Question 4.
$\frac{2}{3}$ ∗ 10 $\frac{1}{5}$ = _________

Answer:
$\frac{2}{3}$ ∗ 10 $\frac{1}{5}$ = 6(12/15).

Explanation:
In the above-given question,
given that,
2/3 x 10(1/5).
10 x 5 = 50.
50 + 1/5 = 51/5.
5 x 3 = 15.
51 x 1/2 = 102/15.

Everyday Math Grade 5 Home Link 8.4 Answer Key

Milk Carton Volume

Myles poured milk from a carton into glasses for his family for breakfast on Monday and Tuesday. Each day he poured 200 cubic centimeters of milk for each of his 2 sisters and himself. He also poured 300 cubic centimeters of milk for his mom and the same amount for his dad.

The milk carton is a rectangular prism. The length is 15 centimeters and the width is 10 centimeters.
Question 1.
What is the minimum height of the milk carton if all of the milk for both days came from one carton? Show your work and explain your answer.

Answer:
The minimum height of the milk carton if all of the milk for both days came from one carton = 16 cms.

Explanation:
In the above-given question,
given that,
Myles poured milk from a carton into glasses for his family for breakfast on Monday and Tuesday.
Each day he poured 200 cubic centimeters of milk for each of his 2 sisters and himself.
He also poured 300 cubic centimeters of milk for his mom and the same amount for his dad.
the milk carton is a rectangular prism.
The length is 15 centimeters and the width is 10 cms.
8 x 2 = 16.
so the minimum height of the milk carton if all of the milk for both days came from one carton = 16 cms.

Practice
Solve. Show your work on the back of this page.
Question 2.
36.4 ÷ 1.3 = _______

Answer:
36.4 ÷ 1.3 = 28.

Explanation:
In the above-given question,
given that,
divide.
36.4 ÷ 1.3.
28.
36.4 ÷ 1.3 = 28.

Question 3.
33.66 ÷ 0.55 = ________

Answer:
33.66 ÷ 0.55 = 61.2

Explanation:
In the above-given question,
given that,
divide.
33.66 ÷ 0.55.
61.2.
33.66 ÷ 0.55 = 61.2.

Everyday Mathematics Grade 5 Home Link 8.5 Answers

Spending $500

Y ou are planning a camping trip for yourself and two friends. After saving money for a few months, you and your friends have $500 to spend on the trip.

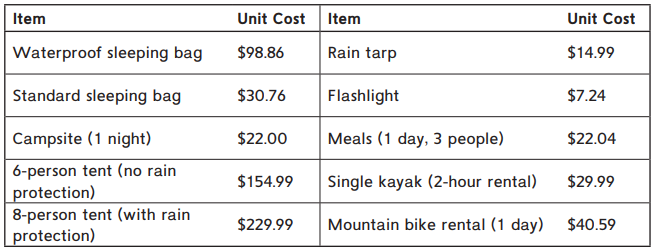
Question 1.
Use the prices above to plan how you will spend $500. Round each unit cost to find approximate total costs. Write a number sentence in the last column to show how you estimated. Spend as clos e to $500 as yo u can.

Answer:
Campsite in 1 night = $522.
6 – person tent (no rain protection) = $654.
8 – person tent (with rain protection) = $729.
Meals (1 day) = $522.04.
Single kayak (2-hour rental) = $529.99.
Mountain bike rental (1 day) = $540.59.

Explanation:
In the above-given question,
given that,
Campsite in 1 night = $22.
6 – person tent (no rain protection) = $154.99.
8 – person tent (with rain protection) = $229.99.
Meals (1 day) = $ 22.04.
Single kayak (2-hour rental) = $29.99.
Mountain bike rental (1 day) = $40.59.

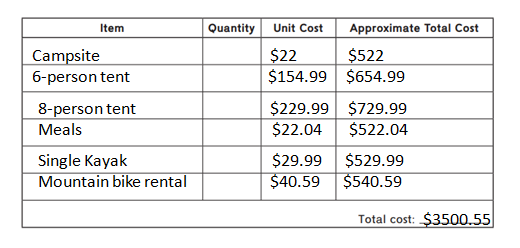
Question 2.
On the back of this page, explain one decision you made as you planned.

Practice
Question 3.
6 $\frac{2}{3}$ ∗ 4 $\frac{7}{8}$ = ________

Answer:
6 $\frac{2}{3}$ ∗ 4 $\frac{7}{8}$ =780/24.

Explanation:
In the above-given question,
given that,
6 $\frac{2}{3}$ ∗ 4 $\frac{7}{8}$.
6 x 3 = 18.
18 + 2/3 = 20/3.
4 x 8 = 32.
32 + 7/8 = 39/8.
20/3 x 39/8 = 780/24.

Question 4.
10$\frac{5}{6}$ ∗ 5 $\frac{3}{4}$ = ________

Answer:
10$\frac{5}{6}$ ∗ 5 $\frac{3}{4}$ = 1495/24.

Explanation:
In the above-given question,
given that,
10 $\frac{5}{6}$ ∗ 5 $\frac{3}{4}$.
10 x 6 = 60.
60 + 5/6 = 65/6.
5 x 4 = 20.
20 + 3/4 = 23/4.
65/6 x 23/4 = 1495/24.

Everyday Math Grade 5 Home Link 8.6 Answer Key

Calculating Earnings

Solve. Show your work. Write a number model to show how you solved.
Question 1.
Jeremiah mows his neighbor’s lawn to earn money. His neighbor pays him $50 per month. It takes Jeremiah 1 hour and 15 minutes to mow the lawn once. He mows the lawn 4 times per month.
a. How many hours does Jeremiah spend mowing the lawn each month?
Number model: __________

Answer:
The number of hours does Jeremiah spends mowing the lawn each month = 5 hours.

b. How much money does Jeremiah earn per hour?
Number model: __________

Answer:
The money does Jeremiah earns per hour = $10.

c. How long would it take Jeremiah to earn $1,000? Give your answer in both months and hours.
Number model(s): __________
Jeremiah would have to work for __________ months, or __________ hours.

Answer:
The number of months would it take Jeremiah to earn $1,000 = 20 months.

Explanation:
In the above-given question,
given that,
Jeremiah mows his neighbor’s lawn to earn money.
His neighbor pays him $50 per month.
It takes Jeremiah 1 hour and 15 minutes to mow the lawn once.
He mows the lawn 4 times per month.
for 1 month = $ 100.
100 x 100 = 1000.
so the number of months would it take Jeremiah to earn $1000 = 20 months.
Practice
Solve using common denominators. Show your work.
Question 2.
8 ÷ $\frac{1}{5}$ = ?
8 ÷ $\frac{1}{5}$ = ________

Answer:
8 ÷ $\frac{1}{5}$ = 40.

Explanation:
In the above-given question,
given that,
8 ÷ $\frac{1}{5}$.
8 ÷ 1/5.
8 x 5 = 40.
8 ÷ $\frac{1}{5}$ = 40.

Question 3.
$\frac{1}{4}$ ÷ 12 = ?
$\frac{1}{4}$ ÷ 12 = ________

Answer:
$\frac{1}{4}$ ÷ 12 =1/48.

Explanation:
In the above-given question,
given that,
$\frac{1}{4}$ ÷ 12.
12 x 4 = 48.
1 x 1/48 = 1/48.

Everyday Mathematics Grade 5 Home Link 8.7 Answers

Paying Off Debts

Solve Problems 1–3. Write a number model to show how you solved.
Question 1.
Kendall lent Kel $40 to buy a game. Kel is earning money by washing cars. He charges $7 per car. How many cars will Kel need to wash in order to pay Kendall back?
Number model: ___________

Answer:
The number of cars will Kel need to wash in order to pay Kendall back = 6 cars.

Explanation:
In the above-given question,
given that,
Kendall lent Kel $40 to buy a game.
Kel is earning money by washing cars.
He charges $7 per car.
6 x $7 = 42.
so the The number of cars will Kel need to wash in order to pay Kendall back = 6 cars.

Question 2.
Josie borrowed $65 from her mom for a class trip to Washington, D.C. When she returns from the trip, Josie will start working for her neighbors. She will make $8.50 each time she walks their dogs.
a. How many times will Josie have to walk the dogs in order to repay her debt?
Number model: ______________

Answer:
The number of times will Josie have to walk the dogs in order to repay her debt = 8 times.

Explanation:
In the above-given question,
given that,
Josie borrowed $65 from her mom for a class trip to Washington, D.C.
When she returns from the trip Josie will start working for her neighbors.
She will make $8.50 each time she walks their dogs.
$8.50 x $8.50 = $65.
8 x 8 = 64.
$50 + $50 = $100.
64 + 1 = 65.
so the number of times will Josie have to walk the dogs in order to repay her debt = 8 times.

b. If Josie walks 3 miles each time she takes the dogs out, how many miles will she have walked by the time she repays her debt?
Number model: ______________

Answer:
The number of miles she walked by the time she repays her debt = 24 miles.

Explanation:
In the above-given question,
given that,
If Josie walks 3 miles each time she takes the dogs out.
3 x 8 = 24 miles.
so the number of miles she walked by the time she repays her debt = 24 miles.

Question 3.
Langdon earns $23 an hour at a law office. He works about 55 hours per week.
a. If there are about 4 weeks in one month, how much money does Langdon earn each month?
Number model: ______________
Answer: About __________

Answer:
The money does Langdon earn a month = $5060

Explanation:
In the above-given question,
given that,
Langdon earns $23 an hour at a law office.
He works about 55 hours per week.
$23 x 55 = 1265.
1265 x 4 = 5060.
so the money does Langdon earn a month = $5060.

b. Langdon took out a $5,000 loan to help pay for college. Would one month’s earnings pay off his loan?

Answer:
Yes.

Explanation:
In the above-given question,
given that,
Langdon took out a $5,000 loan to help pay for college.
the money does Langdon earns a month = $5060.
so the money he earns for 1 month is enough to pay the loan.

Practice
Question 4.
4.53 ∗ 10³ = ________

Answer:
4.53 ∗ 10^{3 = 4530.}

Explanation:
In the above-given question,
given that,
multiply.
4.53 x 10 x 10 x 10.
10 x 10 x 10 = 1000.
4.53 x 1000 = 4530.

Question 5.
62.8 ÷ 10⁴ = ________

Answer:
62.8 ÷ 10^{4 = 0.00628.}

Explanation:
In the above-given question,
given that,
divide.
6.28 ÷ 10^{4.

6.28 x 10 x 10 x 10 x 10.

6.28 x 10000.

0.00628.}

Question 6.
29.1 ∗ 10⁶ = ________

Answer:
29.1 ∗ 10⁶ = 29,100.000.

Explanation:
In the above-given question,
given that,
multiply.
29.1 x 10 x 10 x 10 x 10 x 10 x 10.
29.1 x 1000000.
29,100.000.

Question 7.
7,354.2 ÷ 10² = __________

Answer:
7,354.2 ÷ 10^{2 = 73.542.}

Explanation:
In the above-given question,
given that,
divide.
7354.2 ÷ 10 x 10.
7354.2 ÷ 100.
73.542.

Everyday Math Grade 5 Home Link 8.8 Answer Key

Hiking a New Zealand Trail

Use the information from journal page 300 to fill in the blank.
Length of one footstep: About ________ feet

A group of hikers in New Zealand is walking to a campsite. They will hike from Wellington to Ruapehu, a distance of about 200 miles. Then they will follow a trail for another 12 miles to their campsite. (The campsite is not shown on the map.) Use your class information about step length to solve the problems. Reminder: 1 mile = 5,280 feet
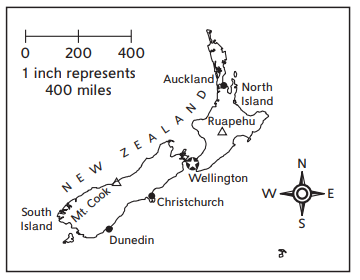
$Everyday Math Grade 5 Home Link 8.8 Answer Key 1$
Question 1.
About how many total miles is it from Wellington to the campsite?
About ________ miles

Answer:
The number of total miles is it from wellington to the campsite = 212 miles.

Explanation:
In the above-given question,
given that,
They will hike from Wellington to Ruapehu, a distance of about 200 miles.
1 inch represents = 400 miles.
200 + 12 = 212.
so the number of total miles is it from wellington to the campsite = 212 miles.

Question 2.
About how many steps would a hiker take to walk from Wellington to the campsite? Show your work below.
About ________ miles

Answer:
The number of steps would a hiker take to walk from wellington to the campsite = 11,19,360 feet.

Explanation:
In the above-given question,
given that,
They will hike from Wellington to Ruapehu, a distance of about 200 miles.
1 inch represents = 400 miles.
200 + 12 = 212.
1 mile = 5280 feet.
212 x 5280 = 11,19,360 feet.
so number of steps would a hiker take to walk from wellington to the campsite = 11,19,360 feet.

Practice
Question 3.
2 $\frac{2}{3}$ ∗ 4 $\frac{1}{5}$ = ?
2 $\frac{2}{3}$ ∗ 4 $\frac{1}{5}$ = __________

Answer:
2 $\frac{2}{3}$ ∗ 4 $\frac{1}{5}$ =168/15.

Explanation:
In the above-given question,
given that,
multiply.
2 x 3 = 6.
6 + 2/3 = 8/3.
4 x 5 = 20.
20 + 1/5 = 21/5.
5 x 3 = 15.
8/3 x 21/5 = 168/15.

Question 4.
9 $\frac{1}{2}$ ∗ 3 $\frac{5}{6}$ = ?
2 $\frac{2}{3}$ ∗ 4 $\frac{1}{5}$ = ________

Answer:
9 $\frac{1}{2}$ ∗ 3 $\frac{5}{6}$ = 437/12.

Explanation:
In the above-given question,
given that,
multiply.
9 x 2 = 18.
18 + 1/2 = 19/2.
3 x 6 = 18.
18 + 5/6 = 23/6.
6 x 2 = 12.
19/2 x 23/6 = 437/12.

Everyday Mathematics Grade 5 Home Link 8.9 Answers

How Many Blueberries?

Question 1.
Fill in the blanks.
1 pint = __________ cups
1 quart = __________ pints

Answer:
1 pint = 2 cups.
1 quart = 2 pints.

Explanation:
In the above-given question,
given that,
1 pint = 2 cups.
1 quart = 2 pints.

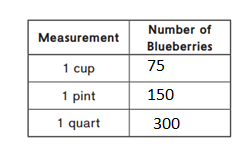
Question 2.
About 75 blueberries fill a 1-cup container.
Use this information and your answers to Problem 1 to help you complete the table.
Hint: If 75 blueberries are in 1 cup, how can you find how many are in 2 cups?

Answer:
The number of blueberries = 75.
the number of blueberries in 1 pint = 150.
the number of blueberries in 1 quart = 300.

Explanation:
In the above-given question,
given that,
About 75 blueberries fill a 1-cup container.
1 pint = 2 cups.
1 quart = 2 pints.
75 = 75.
75 x 2 = 150.
150 x 2 = 300.
The number of blueberries = 75.
the number of blueberries in 1 pint = 150.
the number of blueberries in 1 quart = 300.

Question 3.
One blueberry plant can produce 4 quarts of blueberries in 1 year. How many blueberries does one plant produce in 1 year? Explain how you know.

Answer:
The number of blueberries does one plant can produce in 1 year = 1200.

Explanation:
In the above-given question,
given that,
One blueberry plant can produce 4 quarts of blueberries in 1 year.
300 x 4 = 1200.
so the number of blueberries does one plant can produce in 1 year = 1200.

Question 4.
A farmer can fit about 1,100 blueberry plants in a 1-acre field. About how many blueberries would a well-tended blueberry field produce in 1 year?
About __________ blueberries

Answer:
The number of blueberries would a well-tended blueberry field produces in 1 year = 1320000 blueberries.

Explanation:
In the above-given question,
given that,
A farmer can fit about 1,100 blueberry plants in a 1-acre field.
1100 x 1200.
1320,000.
so the number of blueberries would a well-tended blueberry field produces in 1 year = 1320000 blueberries.

Question 5.
With proper maintenance, a blueberry plant can live for 20 years.
a. Suppose you have one blueberry plant in your backyard. About how many blueberries would it produce in its lifetime?
About __________ blueberries

Answer:
The number of blueberries would it produce in its lifetime = 24000.

Explanation:
In the above-given question,
given that,
a blueberry plant can live for 20 years.
12 x 20 = 24000.
so the number of blueberries would it produce in its lifetime = 24000.

b. Suppose a farmer had a 1-acre blueberry field. About how many blueberries would the field produce in the plants’ lifetime?
About __________ blueberries

Answer:
The number of blueberries would the field produces in the plant’s lifetime = 26,400,000.

Explanation:
In the above-given question,
given that,
suppose a farmer had a 1-acre blueberry field.
300 x 1200 = 26,400,000.
so the number of blueberries would the field produces in the plant’s lifetime = 26,400,000.

Practice
Estimate. Then multiply. Show your work on the back of this page.
Question 6.
23.3 ∗ 1.28 = _______
Estimate: _________

Answer:
23.3 x 1.28 = 29.824.

Explanation:
In the above-given question,
given that,
multiply.
23.3 x 1.28.
29.824.
23.3 x 1.28 = 29.824.

Question 7.
326.2 ∗ 0.52 = __________
Estimate: __________

Answer:
326.2 x 0.52 = 169.624.

Explanation:
In the above-given question,
given that,
multiply.
326.2 x 0.52.
169.624.
326.2 x 0.52 = 169.624.

Everyday Math Grade 5 Home Link 8.10 Answer Key

Cardiac Output

Today you learned that cardiac output is the amount of blood a heart pumps in 1 minute. You can find your cardiac output using your heart rate and the amount of blood your heart pumps with each heartbeat.
Cardiac output = heart rate ∗ amount of blood pumped with each heartbeat

Question 1.
The typical resting heart rate for a healthy adult is about 72 beats per minute. A healthy adult heart pumps about 2.4 fluid ounces of blood per heartbeat.
a. What is the cardiac output of a healthy adult?
__________ beats per minute ∗ __________ fluid ounces of blood per heartbeat = __________ fluid ounces of blood per minute

Answer:
The number of beats per minute = 72.
A healthy adult heart pumps about 2.4 fluid ounces of blood per heartbeat = 2.4.
The number of fluid ounces of blood per minute = 172.8.

Explanation:
In the above-given question,
given that,
The typical resting heart rate for a healthy adult is about 72 beats per minute.
A healthy adult heart pumps about 2.4 fluid ounces of blood per heartbeat.
72 x 2.4 = 172.8.
so the number of fluid ounces of blood per minute = 172.8.

b. How many fluid ounces of blood will a healthy adult’s heart pump in one hour?
About ________ fluid ounces

Answer:
The healthy adult’s heart pump in one hour = 10.368.

c. How many cups of blood is that? About ________ cups

Answer:
The number of cups = 1296.

Explanation:
In the above-given question,
given that,
1 pint = 2 cups.
1 quart = 2 pints.
172.8 x 2 = 1296.
so the number of cups = 1296.

Question 2.
A newborn baby’s heart beats about 135 times per minute, but it pumps only about 0.25 fluid ounce of blood per heartbeat.
a. What is the cardiac output of a newborn baby?
__________ beats per minute ∗ __________ fluid ounces of blood per heartbeat = __________ fluid ounces of blood per minute

Answer:
The number of fluid ounces of blood per minute = 33.75.

Explanation:
In the above-given question,
given that,
A newborn baby’s heart beats about 135 times per minute,
but it pumps only about 0.25 fluid ounce of blood per heartbeat.
135 x 0.25 = 33.75.
so The number of fluid ounces of blood per minute = 33.75.

b. How many fluid ounces of blood will a newborn baby’s heart pump in one hour?
About __________ fluid ounces

Answer:
The newborn baby’s heart pump in one hour = 2.025.

Explanation:
In the above-given question,
given that,
A newborn baby’s heart beats about 135 times per minute,
but it pumps only about 0.25 fluid ounces of blood per heartbeat.
135 x 0.25 = 33.75.
so The number of fluid ounces of blood per minute = 33.75.
1 hour = 60 minutes.
33.75 x 60 = 2.025.

c. How many cups of blood is that? About __________ cups

Answer:
The number of cups of blood is = 253.

Practice
Estimate. Then divide. Show your work.
Question 3.
361.2 ÷ 14 = ?
Estimate: _________
361.2 ÷ 14 = _________

Answer:
361.2 ÷ 14 = 25.8.

Explanation:
In the above-given question,
given that,
divide.
361.2 ÷ 14.
25.8.

Question 4.
7.28 ÷ 0.8 = ?
Estimate: _________
7.28 ÷ 0.8 = ________

Answer:
7.28 ÷ 0.8 = 9.1.

Explanation:
In the above-given question,
given that,
divide.
7.28 ÷ 0.8.
9.1.

Everyday Mathematics Grade 5 Home Link 8.11 Answers

Latitude and Temperature

Latitude is a measure of how far north or south a location is from the equator. This table shows the approximate latitude and average high temperature in April for five cities.

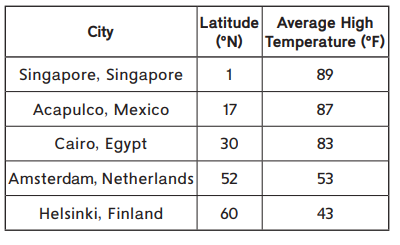
Question 1.
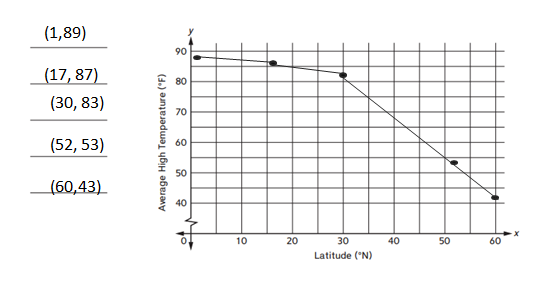
Write the data as ordered pairs. The latitudes are the x-coordinates. The average high temperatures for April are the y-coordinates. Graph the points and use line segments to connect them.

Answer:
The ordered pairs are (1,89), (17, 87), (30,83), (52, 53), (60, 43).

Explanation:
In the above-given question,
given that,
Latitude is a measure of how far north or south a location is from the equator.
The latitudes are the x-coordinates.
The average high temperatures for April are the y-coordinates.
the city of Singapore = 1 and 89.
Acapulco and Mexico = 17 and 87.
Cairo and Egypt = 30 and 83.
Amsterdam and Netherlands = 52 and 53.
so they can be written in ordered pairs are (1,89), (17, 87), (30,83), (52, 53), (60, 43).

Question 2.
The city of Nassau, Bahamas, is located at latitude 25°N. Based on your graph, what would you predict for the average high temperature in Nassau in April?

Answer:
About 84°F.

Explanation:
In the above-given question,
given that,
The city of Nassau, Bahamas, is located at latitude 25°N.
by seeing the graph we can notice the temperature of Nassau.
so the average temperature in Nassau in April is 84°F.

Question 3.
Does latitude seem to have an effect on average high temperature? Explain your answer.

Answer:
Yes.

Explanation:
In the above-given question,
given that,
As the latitude increases, the average temperature seems to go down.
I can tell because as you move to the right on the graph, the point gets lower.
yes, the latitude seems to have an effect on average high temperature.

Everyday Math Grade 5 Home Link 8.12 Answer Key

The Boiling Point

The boiling point of water is the temperature at which it boils. The graphs show how altitude and salt affect the boiling point of water. (Altitude is the measure of how high a location is.) Study the graphs. Then use the m to answer the questions.
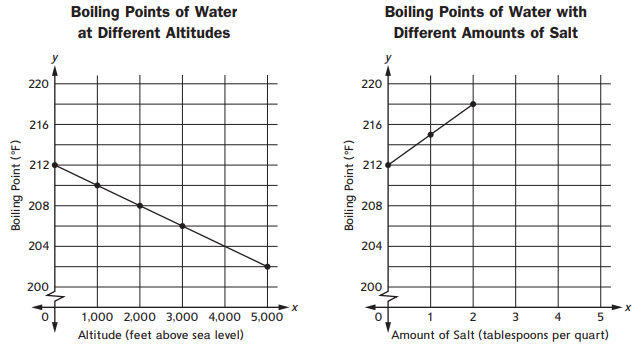
$Everyday Math Grade 5 Home Link 8.12 Answer Key 1$

Question 1.
What would you expect the boiling point of water to be at an altitude of 2,500 feet above sea level?
About _________

Answer:
The boiling point of water to be at an altitude of 2500 feet above sea level = 207°F.

Explanation:
In the above-given graph,
given that,
by seeing the above graph we can notice that the boiling point of water to be at an altitude of 2000 feet above sea level = 208.
so the boiling point of water to be at an altitude of 2500 feet above sea level = 207°F.

Question 2.
What would you expect the boiling point of a quart of water to be if it contained $\frac{1}{2}$ tablespoon of salt?
About _________

Answer:
The boiling point of a quart of water to be if it contained 1/2 tablespoon of salt = 214°F.

Explanation:
In the above-given graph,
given that,
by seeing the above graph we can notice that the boiling point of water to be at an altitude of salt = 214.
so the boiling point of a quart of water to be if it contained 1/2 tablespoon of salt = 214°F.

Question 3.
How does altitude affect the boiling point of water?

Answer:
The altitude affects the boiling point of water decreases.

Explanation:
In the above-given graph,
given that,
On x-axis altitude.
on y-axis boiling point.
so the altitude affects the boiling point of water decreases.

Question 4.
How does salt affect the boiling point of water ?

Answer:
The salt affects the boiling point of water increases.

Explanation:
In the above-given graph,
given that,
On x-axis amount of salt.
on y-axis boiling point.
so the salt affects the boiling point of water increases.

Practice
Divide using the common denominator method. Show your work on the back of this page.
Question 5.
$\frac{1}{4}$ ÷ 6 = ________

Answer:
6 ÷ $\frac{1}{4}$ = 1/24.

Explanation:
In the above-given question,
given that,
6 ÷ $\frac{1}{4}$.
6 ÷ 1/4.
6 x 4 = 24.
6 ÷ $\frac{1}{4}$ = 1/24.

Question 6.
5 ÷ $\frac{1}{10}$= ________

Answer:
5 ÷ $\frac{1}{10}$ = 50.

Explanation:
In the above-given question,
given that,
5 ÷ $\frac{1}{10}$.
5 ÷ 1/10.
10 x 5 = 50.
5 ÷ $\frac{1}{10}$ = 50.