Everyday Math Grade 5 Answers Unit 7 Multiplication of Mixed Numbers; Geometry; Graphs

Everyday Mathematics 5th Grade Answer Key Unit 7 Multiplication of Mixed Numbers; Geometry; Graphs

Everyday Mathematics Grade 5 Home Link 7.1 Answers

Mixed-Number Multiplication

For Problems 1 and 2:

• Use the rectangle to make an area model. Label the sides. The model in Problem 1 has been started for you.
• Find and list the partial products. Label the partial products in the area model.
• Add the partial products to find your answer. You may need to rename fractions with a common denominator .

Question 1.
4\(\frac{3}{8}\) ∗ 5 = ?
Partial products:
4\(\frac{3}{8}\) ∗ 5 = _________

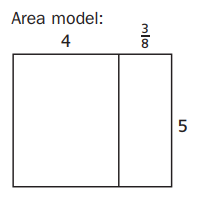
Answer:
20 x 15/8.

Explanation:
In the above-given question,
given that,
the length of the large rectangle = 4.
the length of the small rectangle = 3/8.
the width of the larger rectangle = 5.
the width of the smaller rectangle = 5.
area = l x w.
where l = length, and w = width.
area = 3/8 x 5.
area = 15/8.
area = 5 x 4.
area = 20.
area = 20(15/8).

Question 2.
2\(\frac{3}{5}\) ∗ 3\(\frac{1}{3}\) = ?
Partial products:
2\(\frac{3}{5}\) ∗ 3\(\frac{1}{3}\) = _________
Area Model:

Answer:
8(10/15).

Explanation:
In the above-given question,
given that,
the length of the large rectangle = 4.
the length of the small rectangle = 5/5.
the width of the larger rectangle = 2.
the width of the smaller rectangle =2/3 .
area = l x w.
where l = length, and w = width.
area = 4 x 2.
area = 8.
area = 5/5 x 2/3.
area = 10/15.
8(10/15).

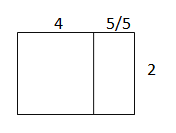
Question 3.
Write a number story that matches Problem 1.

Answer:
20 x 15/8.

Explanation:
In the above-given question,
given that,
the length of the large rectangle = 4.
the length of the small rectangle = 3/8.
the width of the larger rectangle = 5.
the width of the smaller rectangle = 5.
area = l x w.
where l = length, and w = width.
area = 3/8 x 5.
area = 15/8.
area = 5 x 4.
area = 20.

Practice
Solve.
Question 4.
\(\frac{2}{3}\) + \(\frac{5}{8}\) = _________

Answer:
2/3 + 5/8 = 31/24.

Explanation:
In the above-given question,
given that,
\(\frac{2}{3}\) + \(\frac{5}{8}\).
8 x 3 = 24.
24 + 2 = 26.
26 + 5 = 31.
2/3 + 5/8 = 31/24.

Question 5.
\(\frac{1}{16}\) + \(\frac{3}{4}\) = ___________

Answer:
1/16 + 3/4 = 13/16.

Explanation:
In the above-given question,
given that,
\(\frac{1}{16}\) + \(\frac{3}{4}\).
4 x 4 = 16.
4 x 3 = 12.
12 + 1 = 13.
1/16 + 3/4 = 13/16.

Everyday Math Grade 5 Home Link 7.2 Answer Key

More Mixed-Number Multiplication

Solve Problems 1 and 2 using the method in the example below. Show your work.
Example: 2\(\frac{1}{5}\) ∗ 1\(\frac{3}{4}\)

• Rename any mixed or whole numbers as fractions: 2\(\frac{1}{5}\) = \(\frac{11}{5}\); 1\(\frac{3}{4}\) = \(\frac{7}{4}\)
• Rewrite the problem using the fractions as factors: \(\frac{11}{5}\) * \(\frac{7}{4}\)
• Multiply using a fraction multiplication algorithm: \(\frac{(11 * 7)}{(5 * 4)}=\frac{77}{20}\), or 3\(\frac{17}{20}\)

Question 1.
1\(\frac{3}{5}\) ∗ 6 = ?
1\(\frac{3}{5}\) ∗ 6 = __________

Answer:
48/5.

Explanation:
In the above-given question,
given that,
1\(\frac{3}{5}\) ∗ 6.
1\(\frac{3}{5}\) = \(\frac{8}{5}\).
8/5 x 6.
6 x 8 = 48.
48/5.

Question 2.
4\(\frac{1}{2}\) ∗ 1\(\frac{5}{6}\) = ?
4\(\frac{1}{2}\) ∗ 1\(\frac{5}{6}\) = __________

Answer:
99/12.

Explanation:
In the above-given question,
given that,
4\(\frac{1}{2}\) ∗ 1\(\frac{5}{6}\).
\(\frac{9}{2}\) ∗ \(\frac{11}{6}\).
latex]\frac{(11 * 9)}{(6 * 2)}=\frac{99}{12}[/latex]
99/12.

Solve Problems 3 and 4 using the method of your choice.
Question 3.
What is the area of a table that is 1\(\frac{1}{4}\) m long and 2\(\frac{1}{3}\) m wide? Write a number model with a letter for the unknown. Then solve. Show your work.
Number model: _________________
The area of the table is _________________ m².

Answer:
The area of the table is 35/12 sq m.

Explanation:
In the above-given question,
given that,
1\(\frac{1}{4}\) ∗ 2\(\frac{1}{3}\).
\(\frac{5}{4}\) ∗ \(\frac{7}{3}\).
latex]\frac{(5 * 7)}{(6 * 2)}=\frac{35}{12}[/latex]
5 x 7 = 35.
4 x 3 = 12.
35/12.
so the area of the table is 35/12 sq m.

Question 4.
Write a number story that can be solved by multiplying 2\(\frac{3}{4}\) and \(\frac{1}{2}\). Then solve the problem. Show your work on the back of this page.
Number story:

Answer:
11/8.

Explanation:
In the above-given question,
given that,
2\(\frac{3}{4}\) ∗ \(\frac{1}{2}\).
\(\frac{11}{4}\) ∗ \(\frac{1}{2}\).
latex]\frac{(11 * 1)}{(4 * 2)}=\frac{11}{8}[/latex]

Practice
Question 5.
\(\frac{11}{12}\) – \(\frac{3}{4}\) = ________

Answer:
\(\frac{11}{12}\) – \(\frac{3}{4}\) = 2/12.

Explanation:
In the above-given question,
given that,
\(\frac{11}{12}\) – \(\frac{3}{4}\).
14 – 2/12.
2/12 = 1/6.

Question 6.
\(\frac{7}{8}\) – \(\frac{1}{6}\) = _________

Answer:
\(\frac{7}{8}\) – \(\frac{1}{6}\) = 17/24.

Explanation:
In the above-given question,
given that,
\(\frac{7}{8}\) – \(\frac{1}{6}\).
lcm of 6 and 8 = 24.
7 x 3 = 21.
1 x 4 = 4.
21 – 4 = 17.
17/24.

Everyday Mathematics Grade 5 Home Link 7.3 Answers

Solving More Area Problems

Solve. Sho w your work. Write a number model to summarize each solution.
Question 1.
The cover of Martina’s book measures 7\(\frac{1}{4}\) inches by 9 inches. What is the area of the book cover?
Area: ____________
Number Model: ____________

Answer:
The area of the book cover = 65(1/4) sq in.

Explanation:
In the above-given question,
given that,
The cover of Martina’s book measures 7(1/4) inches by 9 inches.
7(1/4) = 7 x 4 = 28.
28 + 1 = 29.
29 x 9 = 261.
261/4.
so the area of the book cover = 261/4 sq in.

Question 2.
The hallway floor in Ryan’s school is covered with square tiles that are \(\frac{1}{2}\) foot by \(\frac{1}{2}\) foot. Ryan counted and found that the hallway is 15 tiles wide and 60 tiles long.
a. How many tiles cover the hallway floor?
b. What is the area of the hallway floor?
Area: ____________
Number Model: ____________

Answer:
a.The number of tiles cover the hallway floor = 900 tiles.
b. The area of the hallway floor = 225 sq ft.

Explanation:
In the above-given question,
given that,
The hallway floor in Ryan’s school is covered with square tiles that are 1/2 foot by 1/2.
Ryan counted and found that the hallway is 15 tiles wide and 60 tiles long.
60 x 15.
60 x 15 = 900.
so no of tiles = 900 tiles.
area = 15 x 15.
area = 225 sq ft.

Question 3.
An artist made a stained-glass window that is 3\(\frac{1}{2}\) feet by 2 \(\frac{3}{4}\) feet.
a. What is the area of the window?
Area: ____________
Number Model: ____________

Answer:
The area of the window = 77/8 sq ft.

Explanation:
In the above-given question,
given that,
An artist made a stained-glass window that is 3(1/2) feet by 2(3/4).
3 x 2 = 6.
6 + 1/2 = 7/2.
4 x 2 = 8.
8 + 3/4 = 11/4.
7/2 x 11/4.
11 x 7 = 77.
4 x 2 = 8.
77/8.
so the area of the window = 77/8 sq ft.

b. The artist’s design used squares of colored glass that measure \(\frac{1}{4}\) foot by \(\frac{1}{4}\) foot. How many colored squares did the artist use?
Area: ____________
Number Model: ____________

Answer:
The number of colored squares did the artist use = 154 tiles.

Explanation:
In the above-given question,
given that,
The artist’s design used squares of colored glass that measure 1/4 foot by 1/4.
4 x 4 = 16.
16 x 9 = 144.
144 + 10 = 154.
so the number of colored squares did the artist use = 154 tiles.

Practice
Question 4.
3\(\frac{1}{8}\) + 4\(\frac{2}{3}\) = _________

Answer:
3\(\frac{1}{8}\) + 4\(\frac{2}{3}\) = 187.

Explanation:
In the above-given question,
given that,
3\(\frac{1}{8}\) + 4\(\frac{2}{3}\).
3(1/8) + 4(2/3).
3 x 8 = 24.
24 + 1/8 = 25/8.
4 x 3 = 12.
12 + 2/3 = 14/3.
lcm of 8 and 3 = 24.
25 x 3 = 75.
14 x 8 = 112.
112 + 75 = 187.

Question 5.
2\(\frac{1}{6}\) + 1\(\frac{5}{8}\) = __________

Answer:
2\(\frac{1}{6}\) + 1\(\frac{5}{8}\) = 62/18.

Explanation:
In the above-given question,
given that,
2\(\frac{1}{6}\) + 1\(\frac{5}{8}\).
2(1/6) + 1(5/8).
6 x 2 = 12.
12 + 1/6 = 13/6.
8 x 1 = 8.
8 + 5/8 = 13/8.
lcm of 6 and 8 = 18.
13 + 3 = 16.
16/18 + 46/18 = 62/18.

Everyday Math Grade 5 Home Link 7.4 Answer Key

Solving Fraction Division Problems

Using Common Denominators to Divide 210
One way to divide fractions is to use common denominators. This method can be used to divide whole numbers by fractions and fractions by whole numbers.
Step 1 Rename the dividend and divisor as fractions with a common denominator
Step 2 Divide the numerators

Example:
\(\frac{1}{3}\) ÷ 4 = \(\frac{1}{3}\) ÷ \(\frac{12}{3}\)
1 ÷ 12 = \(\frac{1}{12}\)

Solve Problems 1–4. Show your work. Use multiplication to check your answer.
Question 1.
5 ÷ \(\frac{1}{3}\)= ?
Check: _______

Answer:
\(\frac{1}{15}\)

Explanation:
In the above-given question,
given that,
5 ÷ \(\frac{1}{3}\).
\(\frac{1}{3}\) ÷ \(\frac{15}{3}\).
1 ÷ 15.
\(\frac{1}{15}\).

Question 2.
4 ÷ \(\frac{1}{8}\) = ?
Check: _______

Answer:
\(\frac{1}{32}\).

Explanation:
In the above-given question,
given that,
4 ÷ \(\frac{1}{8}\).
\(\frac{1}{8}\) ÷ \(\frac{32}{8}\).
1 ÷ 32.
\(\frac{1}{32}\).

Question 3.
\(\frac{1}{6}\) 4 = ?
Check: _______

Answer:
\(\frac{1}{24}\).

Explanation:
In the above-given question,
given that,
4 ÷ \(\frac{1}{6}\).
\(\frac{1}{6}\) ÷ \(\frac{24}{6}\).
1 ÷ 24.
\(\frac{1}{24}\).

Question 4.
\(\frac{1}{5}\) 6 = ?
Check: _________

Answer:
\(\frac{1}{30}\).

Explanation:
In the above-given question,
given that,
6 ÷ \(\frac{1}{5}\).
\(\frac{1}{5}\) ÷ \(\frac{30}{6}\).
1 ÷ 30.
\(\frac{1}{30}\).

Question 5.
Write a number story to match Problem 2.

Answer:
\(\frac{1}{32}\).

Explanation:
In the above-given question,
given that,
4 ÷ \(\frac{1}{8}\).
\(\frac{1}{8}\) ÷ \(\frac{32}{8}\).
1 ÷ 32.
\(\frac{1}{32}\).

Practice
Question 6.
4\(\frac{1}{2}\) – 1\(\frac{3}{4}\) = _________

Answer:
4\(\frac{1}{2}\) – 1\(\frac{3}{4}\) = 11/4.

Explanation:
In the above-given question,
given that,
4\(\frac{1}{2}\) – 1\(\frac{3}{4}\).
4(1/2) – 1(3/4).
4 x 2 = 8.
8 + 1/2 = 9/2.
1 x 4 = 4.
4 + 3/4 = 7/4.
lcm of 2 and 4 is 4.
9 x 2 = 18.
18 – 7 = 11/4.

Question 7.
2\(\frac{7}{8}\) – 1\(\frac{1}{3}\) = __________

Answer:
2\(\frac{7}{8}\) – 1\(\frac{1}{3}\) = 37/24.

Explanation:
In the above-given question,
given that,
2\(\frac{7}{8}\) – 1\(\frac{1}{3}\).
2(7/8) – 1(1/3).
8 x 2 = 16.
16 + 7/8 = 23/8.
1 x 3 = 3.
3 + 1/3 = 4/3.
lcm of 8 and 3 is 24.
23 + 3/8 = 26/8.
4 + 8 = 12/8.
26 + 11 = 37/24.

Everyday Mathematics Grade 5 Home Link 7.5 Answers

Using a Hierarchy

A pentagon is a shape with 5 sides. The shape below is a pentagon.

An equilateral pentagon is a pentagon with 5 sides that are all the same length. The shape below is an equilateral pentagon.

Consider the pentagon hierarchy below. Use it to answer the questions.
Question 1.
Answer Parts a–c to classify this shape on the hierarchy.

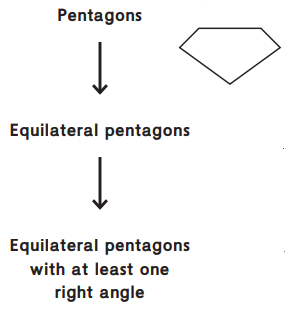
a. Can this shape go in the top category, Pentagons? How do you know?

Answer:
Yes.

Explanation:
In the above-given question,
given that,
pentagons are in the above diagrams.
so the shape belongs to this category.

b. Can this shape go in the first subcategory, Equilateral pentagons? How do you know?

Answer:
No.

Explanation:
In the above-given question,
given that,
Equilateral pentagons are in the second subcategory.
so the shape does not belong to the 1st category.

c. Can this shape go into the second subcategory, Equilateral pentagons with at least one right angle? How do you know?

Answer:
No.

Explanation:
In the above-given question,
given that,
Equilateral pentagons with at least one right angle are in the third subcategory.
so the shape does not belong to the second subcategory.

Question 2.
Describe how you would classify the shape below on the hierarchy. Start at the top and describe how you know if the shape fits in each category and subcategory.

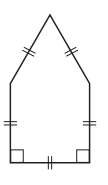
Answer:
The shape fits the Equilateral pentagon.

Explanation:
In the above-given question,
given that,
Equilateral pentagons are in the second subcategory.
so the shape does not belong to the 1st category.

Everyday Math Grade 5 Home Link 7.6 Answer Key

The Quadrilateral Hierarchy

The quadrilateral hierarchy you used in class is below. Use it to answer the questions.

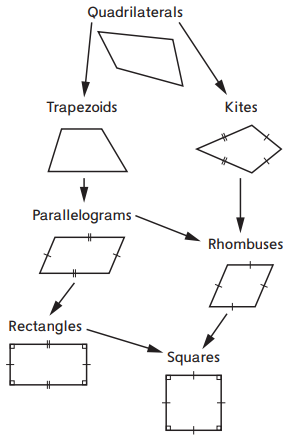
Question 1.
Fill in the blanks
a. All trapezoids are quadrilaterals, but not all quadrilaterals are trapezoids .

b. All __________ are __________, but not all __________ are __________.
c. All __________are __________, but not all __________ are __________

Answer:
a.Yes.
b. All parallelograms are rhombuses, but not all rectangles are squares.

Explanation:
In the above-given question,
given that,
All quadrilaterals are trapezoids and kites.
All trapezoids are parallelograms.
All parallelograms are rectangles.
All parallelograms are rhombuses.
All rhombuses are squares.

Question 2.
a. All parallelograms have two pairs of parallel sides. Does this mean that all rectangles have two pairs of parallel sides? Explain how you can tell by looking at the hierarchy.

Answer:
Yes.

Explanation:
In the above-given question,
given that,
All parallelograms have two pairs of parallel sides.
Yes, it means that all rectangles have two pairs of parallel sides.

b. All trapezoids have at least one pair of parallel sides. Which other shapes have at least one pair of parallel sides? Explain how you can tell by looking at the hierarchy.

Answer:
Yes, All trapezoids have at least one pair of parallel sides.
Rhombuses have at least one pair of parallel sides.
All rectangles are squares.

Explanation:
In the above-given question,
given that,
Yes, All trapezoids have at least one pair of parallel sides.
Rhombuses have at least one pair of parallel sides.
All rectangles are squares.

Practice
Question 3.
\(\frac{1}{4}\) ÷ 8 = ________

Answer:
\(\frac{1}{4}\) ÷ 8 = 1/32.

Explanation:
In the above-given question,
given that,
\(\frac{1}{4}\) ÷ 8.
1/4 ÷ 8.
8 x 4 = 32.
1/32.
\(\frac{1}{4}\) ÷ 8 = 1/32.

Question 4.
\(\frac{1}{10}\) ÷ 3 = __________

Answer:
\(\frac{1}{10}\) ÷ 3 = 1/30.

Explanation:
In the above-given question,
given that,
\(\frac{1}{10}\) ÷ 3.
1/10 ÷ 3.
10 x 3 = 30.
1/30.
\(\frac{1}{10}\) ÷ 3 = 1/30.

Question 5.
\(\frac{1}{6}\) ÷ 2 = ___________

Answer:
\(\frac{1}{6}\) ÷ 2 = 1/12.

Explanation:
In the above-given question,
given that,
\(\frac{1}{6}\) ÷ 2.
1/6 ÷ 2.
6 x 2 = 12.
1/12.
\(\frac{1}{6}\) ÷ 2 = 1/12.

Question 6.
\(\frac{1}{5}\) ÷ 12 = _________

Answer:
\(\frac{1}{5}\) ÷ 12 = 1/60.

Explanation:
In the above-given question,
given that,
\(\frac{1}{5}\) ÷ 12.
1/5 ÷ 12.
12 x 5 = 60.
1/60.
\(\frac{1}{5}\) ÷ 12 = 1/60.

Everyday Mathematics Grade 5 Home Link 7.7 Answers

Property Pandemonium

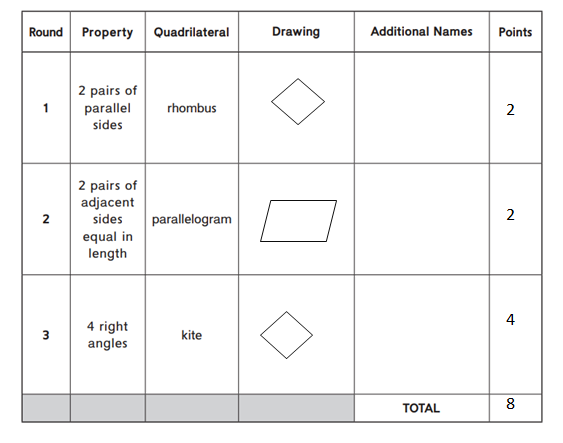
Question 1.
Imagine that you are playing Property Pandemonium. You already chose all of your cards and filled in the Property and Quadrilateral columns. Complete the Drawing, Additional Names, and Points columns for each round. Then find your total score.

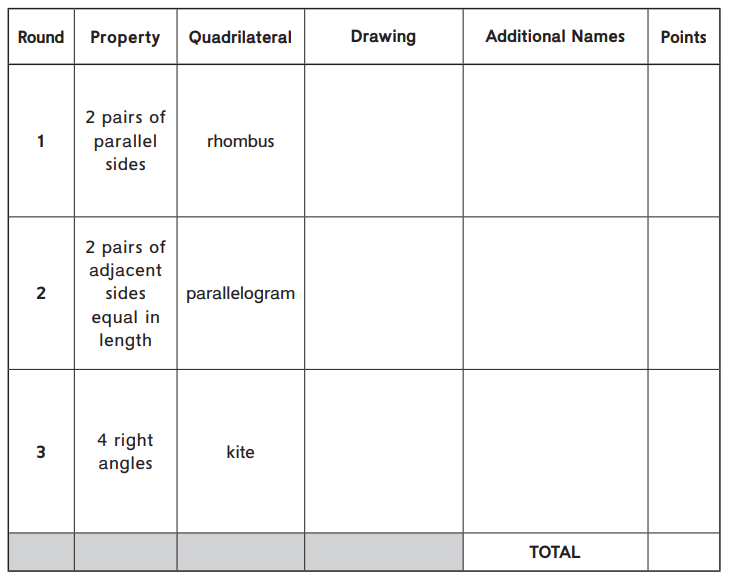
Answer:
The total score = 8.

Explanation:
In the above-given question,
given that,
2 pairs of parallel sides = rhombus.
2 pairs of adjacent sides equal in length = parallelogram.
4 right angles = kite.
2 + 2 + 4 = 8.
the total number of points = 8.

Practice
Divide.
Question 2.
9 ÷ \(\frac{1}{3}\) = _______

Answer:
9 ÷ \(\frac{1}{3}\) = 27.

Explanation:
In the above-given question,
given that,
9 ÷ \(\frac{1}{3}\).
9 x 3 = 27.
9 ÷ \(\frac{1}{3}\) = 27.

Question 3.
4 ÷ \(\frac{1}{5}\) = _________

Answer:
4 ÷ \(\frac{1}{5}\) = 20.

Explanation:
In the above-given question,
given that,
4 ÷ \(\frac{1}{5}\).
5 x 4 = 20.
4 ÷ \(\frac{1}{5}\) = 20.

Question 4.
2 ÷ \(\frac{1}{10}\) = _________

Answer:
2 ÷ \(\frac{1}{10}\) = 20.

Explanation:
In the above-given question,
given that,
2 ÷ \(\frac{1}{10}\).
10 x 2 = 20.
2 ÷ \(\frac{1}{10}\) = 20.

Question 5.
12 ÷ \(\frac{1}{4}\) = __________

Answer:
12 ÷ \(\frac{1}{4}\) = 48.

Explanation:
In the above-given question,
given that,
12 ÷ \(\frac{1}{4}\).
12 x 4 = 48.
12 ÷ \(\frac{1}{4}\) = 48.

Everyday Math Grade 5 Home Link 7.8 Answer Key

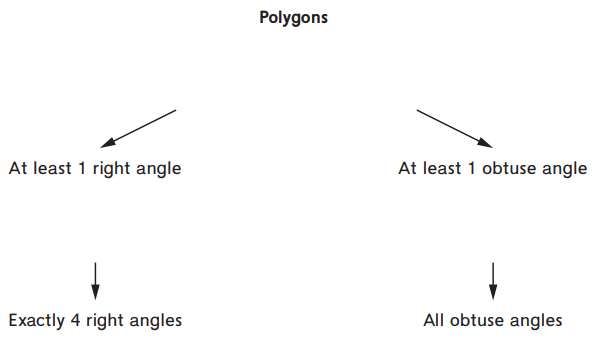
Classifying Polygons

Question 1.
Draw the 12 shapes above in the correct categories on the hierarchy.

Answer:
The shapes that have at least 1 right angle = rhombus.
The shapes that have exactly 4 right angles = 90 degrees.
The shapes that have at least 1 obtuse angle = trapezoid, rhombus, acute angle, diamond shape.
The shapes that have exactly all obtuse angles = hexagon, pentagon, octagon, parallelogram.

Explanation:
In the above-given question,
given that,
the shapes.
The shapes that have at least 1 right angle = rhombus.
The shapes that have exactly 4 right angles = 90 degrees.
The shapes that have at least 1 obtuse angle = trapezoid, rhombus, acute angle, diamond shapes.

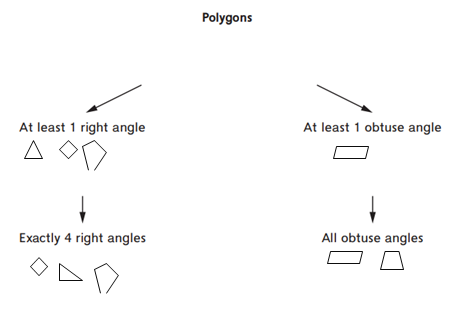
Question 2.
Explain how you decided where to place the hexagon.

Answer:
Hexagon is placed in all obtuse angles.

Explanation:
In the above-given question,
given that,
The shape Hexagon has all the sides 120 degrees.
so hexagon is placed in all obtuse angles.

Practice
Solve.
Question 3.
6.8 ∗ 10³ = ________

Answer:
6.8 x 10^{3 = 6800.}

Explanation:
In the above-given question,
given that,
Multiply.
6.8 x 10^{3.
6.8 x 10 x 10 x 10.
6.8 x 1000.
6800.}

Question 4.
12.7 ÷ 10⁴ = __________

Answer:
12.7 ÷ 10⁴ = 0.00127.

Explanation:
In the above-given question,
given that,
Divide.
12.7 ÷ 10^4.
12.7 ÷ 10 x 10 x 10 x 10.
0.00127.

Question 5.
0.4 ∗ _________ = 4,000

Answer:
0.4 x 10^{4. = 4000.}

Explanation:
In the above-given question,
given that,
Multiply.
0.4 x 10^{4..
0.4 x 10 x 10 x 10 x 10.
4000.}

Question 6.
64.3 ÷ ________ = 0.643

Answer:
64.3 x 10 x 10 = 0.643.

Explanation:
In the above-given question,
given that,
Divide.
64.3 x 10 x 10.
64.3 x 100.
0.643.

Everyday Mathematics Grade 5 Home Link 7.9 Answers

Plotting and Interpreting Line-Plot Data

Marisela and her class are finding their finger-stretch measurements. The finger stretch is measured from the tip of the pinkie to the tip of the index finger with an outstretched hand. Below are the measurements for Marisela and her classmates to the nearest \(\frac{1}{2}\) inch.

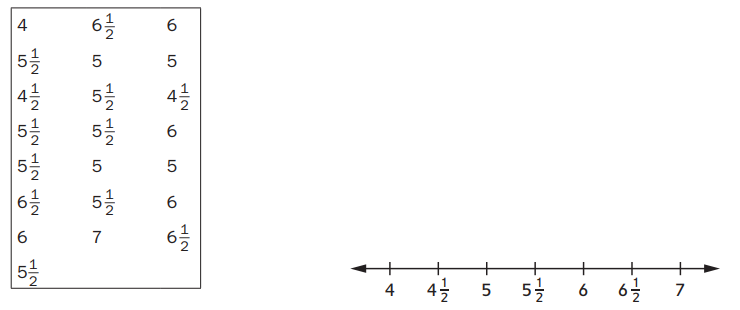
Question 1.
Plot the data on the line plot.

Answer:
The fingers on 4 inches = 1.
4.5 in = 2, 5 in = 4, 5.5 in = 7, 6 in = 4, 6.5 = 3, 7 = 1.

Explanation:
In the above-given question,
given that,
The finger length in inches.
fingers on 4 inches = 1.
4.5 in = 2.
on 5 in = 4.
on 5.5 in = 7.
on 6 in = 4.
on 6.5 in = 3.
on 7 in = 1.

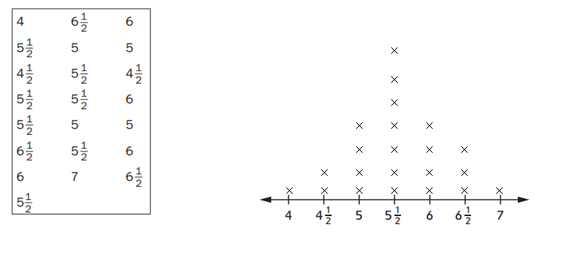
Question 2.
Marisela wants to find the total length of all the 6 \(\frac{1}{2}\)inch finger stretches. Write a number model using addition to help her find the total, then solve.
Number model: __________
________ inches

Answer:
The total length of all 6-inch finger stretches = 39/2.

Explanation:
In the above-given question,
given that,
Marisela wants to find the total length of all the 6(1/2) inch finger stretches.
6 x 2 = 12.
6 x 5 = 30.
30 + 9/2 = 39/2.
so the total length of all 6-inch finger stretches = 39/2.

Question 3.
Now Marisela wants to use multiplication to find the total length of all the 5 \(\frac{1}{2}\) inch finger stretches. Write a number model. Then solve.
Number model: __________
__________ inches

Answer:
The total length of all the 5(1/2) inch finger stretches = 77/2.

Explanation:
In the above-given question,
given that,
Now Marisela wants to use multiplication to find the total length of all the 5(1/2) inch finger stretches.
5 x 2 = 10.
10 + 1/2 = 11/2.
11 x 7/2 = 77/2.

Question 4.
Find the total length of all the finger stretches in Marisela’s class.
__________ inches

Answer:
The total length of all the finger stretches in Marisela’s class = 122.

Explanation:
In the above-given question,
given that,
Now Marisela wants to use multiplication to find the total length of all the 5(1/2) inch finger stretches.
5 x 2 = 10.
10 + 1 = 11.
11 x 12 = 120.
120 + 2 = 122.
so the total length of all the finger stretches in Marisela’s class = 122.

Practice
Question 5.
4 \(\frac{1}{5}\) ∗ \(\frac{1}{3}\) = ________

Answer:
4 \(\frac{1}{5}\) ∗ \(\frac{1}{3}\) = 21/15.

Explanation:
In the above-given question,
given that,
4 \(\frac{1}{5}\) ∗ \(\frac{1}{3}\) .
4(1/5) x 1/3.
5 x 4 = 20.
20 + 1/5 = 21/5.
21/5 x 1/3.
5 x 3 = 15.
4(1/5) x 1/3 = 21/15.

Question 6.
2 \(\frac{5}{6}\) ∗ 7 \(\frac{1}{4}\) = ________

Answer:
2 \(\frac{5}{6}\) ∗ 7 \(\frac{1}{4}\) = 493/24.

Explanation:
In the above-given question,
given that,
2 \(\frac{5}{6}\) ∗ 7 \(\frac{1}{4}\) .
2(5/6) x 7 (1/4).
6 x 2 = 12.
12 + 5/6 = 17/6.
7 x 4 = 28.
28 + 1/4 = 29/4.
lcm of 6 and 4 is 24.
17 + 4 = 21.
29 + 6 = 31.
493/24.

Everyday Math Grade 5 Home Link 7.10 Answer Key

Identifying Patterns

Question 1.
a. Each column in the table below has a rule at the top. Use the rules to fill in the columns.

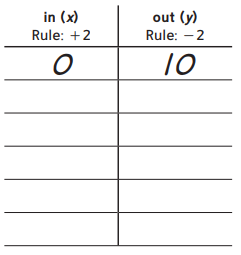
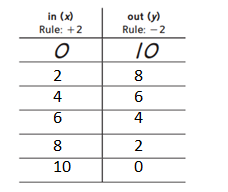
Answer:
In (x) = 2, 4, 6, 8, and 10.
In (Y) = 8, 6, 4, 2, and 0.

Explanation:
In the above-given question,
given that,
in (x) Rule: 0 + 2 = 2.
2 + 2 = 4.
4 + 2 = 6.
6 + 2 = 8.
8 + 2 = 10.
in (Y) Rule: 10 – 2 = 8.
8 – 2 = 6.
6 – 2 = 4.
4 – 2 = 2.
2 – 2 = 0.

b. What rule relates the numbers in the in column to the numbers in the out column? Hint: What happens when you add the numbers in each row?

Answer:
Subtract the numbers in from 10 to get out.

Explanation:
In the above-given question,
given that,
when we add the numbers in each row is
to subtract the numbers in from 10 to get out.

c. Write the numbers from the table as ordered pairs. Graph the ordered pairs on the grid. Draw a line to connect the points.
Ordered pairs:

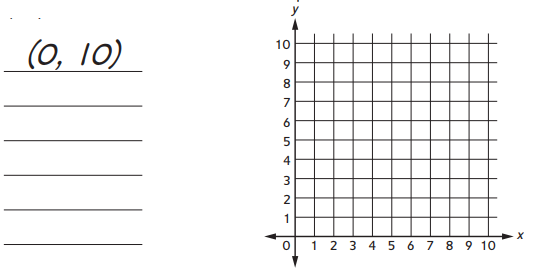
Answer:
The order pairs are (2,8), (6, 4), (8, 2), (10, 0).

Explanation:
In the above-given question,
given that,
write the numbers from the table as ordered pairs.
the ordered pairs are (2,8), (6, 4), (8, 2), (10, 0).

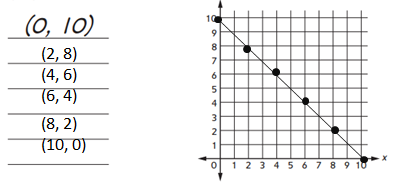
Question 2.
How does your graph in Problem 1c show the + 2 rule from the in column?

Answer:
The graph shows the problem + 2 rule.

Explanation:
In the above-given question,
given that,
in (x) Rule: 0 + 2 = 2.
2 + 2 = 4.
4 + 2 = 6.
6 + 2 = 8.
8 + 2 = 10.
in (Y) Rule: 10 – 2 = 8.
8 – 2 = 6.
6 – 2 = 4.
4 – 2 = 2.
2 – 2 = 0.

Practice
The digits in each product or quotient are given. Use an estimate to place the decimal point. Write a number sentence to show how you estimated.
Question 3.
42.96 ÷ 1.2 = 3 5 8
Number sentence: ___________

Answer:
42.96 ÷ 1.2 = 35.8.

Explanation:
In the above-given question,
given that,
Divide.
42.96 ÷ 1.2.
35.8.

Question 4.
19.2 ∗ 8.8 = 1 6 8 9 6
Number sentence: ___________

Answer:
19.2 ∗ 8.8 = 168.96.

Explanation:
In the above-given question,
given that,
Multiplication.
19.2 x 8.8.
168.96.

Everyday Mathematics Grade 5 Home Link 7.11 Answers

Working with Rules, Tables, and Graphs

Use the rule to complete the table. Write ordered pairs to represent the data. Then graph the ordered pairs and answer the questions.
Question 1.
Cherry tomatoes cost $2.50 per p ound.
Rule: Cost = $2.50 ∗ weight in pounds
a.

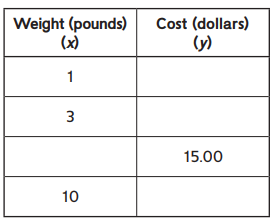
Answer:
The weight in pounds 1 = $2.50, 3 = $7.50, 6 = $15, 10 = $25.00.

Explanation:
In the above-given question,
given that,
Cherry tomatoes cost $2.50 per pound.
2.50 + 2.50 + 2.50 = 7.50.
2.50 x 6 = $15.
2.50 x 10 = $25.00.

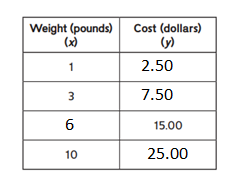
b. Ordered pairs:
___________ ___________ ___________ ___________

Answer:
The ordered pairs are (1, 2.50), (3, 7.50), (6, 15.00), (10, 25.00).

Explanation:
In the above-given question,
given that,
Cherry tomatoes cost $2.50 per pound.
2.50 + 2.50 + 2.50 = 7.50.
2.50 x 6 = $15.
2.50 x 10 = $25.00.
The ordered pairs are (1, 2.50), (3, 7.50), (6, 15.00), (10, 25.00).

c.

Answer:

d. Plot a point to show the cost of 8 pounds of cherry tomatoes. What is the cost?

Answer:
The cost of 8 pounds of cherry tomatoes = $20.00.

Explanation:
In the above-given question,
given that,
Cherry tomatoes cost $2.50 per pound.
2.50 + 2.50 + 2.50 = 7.50.
2.50 x 8 = 20.00.
so the cost of 8 pounds of cherry tomatoes = $20.00.

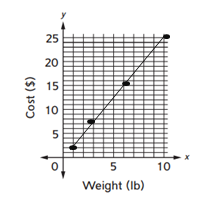
e. Julius has $12.00. Does he have enough money to buy 5 pounds of cherry tomatoes? Explain.

Answer:
No.

Explanation:
In the above-given question,
given that,
Julius has $12.00.
2.50 x 5 = $12.5.
so he does not have enough money.

f. Would you use the graph, the table, or the rule to find out how much 50 pounds of cherry tomatoes would cost? Explain.

Answer:
50 x 2.50 = $125.

Explanation:
In the above-given question,
given that,
50 x 2.50 = $125.

Practice
Multiply. Show your work on the back of this page.
Question 2.
29.5 ∗ 62.3 = ___________

Answer:
29.5 x 62.3 = 1837.85.

Explanation:
In the above-given question,
given that,
Multiply.
29.5 x 62.3.
1837.85.

Question 3.
4.1 ∗ 250.8 = ___________

Answer:
4.1 x 250.8 = 1028.28.

Explanation:
In the above-given question,
given that,
Multiply.
4.1 x 250.8.
1028.28.

Everyday Math Grade 5 Home Link 7.12 Answer Key

Interpreting Tables and Graphs

Ami runs 6 yards per second. Derek runs 5 yards per second. Ami challenged Derek to an 80-yard race. She told him he could have a 12-yard head start.

• Complete the tables to show the distances Ami and Derek are from the starting line during the first 5 seconds of the race.
• Write 3 ordered pairs each for Ami and Derek.
• Graph the ordered pairs you wrote and connect them with a line. Extend each line to the 80-yard mark to find out who wins. Label each line.

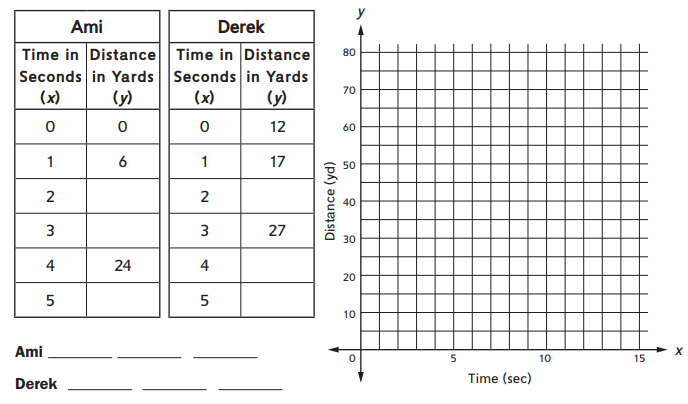
Question 1.
Who wins the race? How do you know?

Answer:
Ami wins the race.

Explanation:
In the above-given question,
given that,
Ami run in seconds 1 = 6 yards.
2 = 12 yds.
3 = 18 yds.
4 = 24 yds.
5 = 30 yds.
Derex run in seconds 0 = 12 yds.
1 = 17 yds.
2 = 22 yds.
4 = 32 yds.
5 = 37 yds.

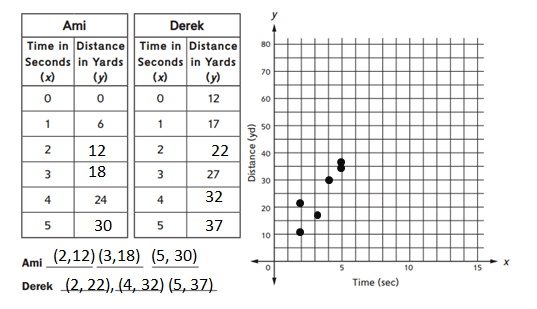
Practice
Write an equivalent problem with a whole-number divisor. Then solve.
Question 2.
68 ÷ 0.5 = ________

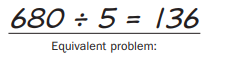
Answer:
68 ÷ 0.5 = 136.

Explanation:
In the above-given question,
given that,
Equivalent problems.
680 ÷ 5.
136.
68 ÷ 0.5 = 136.

Question 3.
7.92 ÷ 0.22 = _________

Answer:
7.92 ÷ 0.22 = 36.

Explanation:
In the above-given question,
given that,
Equivalent problems.
7.92 ÷ 0.22.
36.
7.92 ÷ 0.22 = 36.

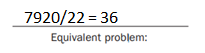
Everyday Mathematics Grade 5 Home Link 7.13 Answers

Analyzing Patterns and Relationships

Question 1.
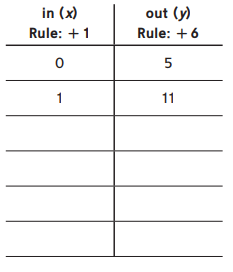
Use the given rules to complete each column of the table.

Answer:
In Rule 1: 2, 3, 4, and 5.
In Rule 2: 17, 23, 29, and 35.

Explanation:
In the above-given question,
given that,
In rule 1 adding 1 to the other number.
In rule 2 adding 6 to the other number.
In Rule 1: 2, 3, 4, and 5.
In Rule 2: 17, 23, 29, and 35.

Question 2.
Find a rule that relates the in numbers to the corresponding out numbers.
Rule: ______________

Answer:
In number x 6 + 5 = out number.

Explanation:
In the above-given question,
given that,
1 x 6 + 5 = 11.
in rule 1 = rule 11.
in number x 6 + 5 = out number.

Question 3.
Write the numbers in the table as ordered pairs.

Answer:
The numbers in ordered pairs are (0,5), (1, 11), (2, 17), (3, 23), (4, 29), (5, 35).

Explanation:
In the above-given question,
given that,
In rule 1 adding 1 to the other number.
In rule 2 adding 6 to the other number.
In Rule 1: 2, 3, 4, and 5.
In Rule 2: 17, 23, 29, and 35.

Question 4.
Graph the ordered pairs on the grid.

Answer:
The numbers in ordered pairs are (0,5), (1, 11), (2, 17), (3, 23), (4, 29), (5, 35).

Explanation:
In the above-given question,
given that,
In rule 1 adding 1 to the other number.
In rule 2 adding 6 to the other number.
In Rule 1: 2, 3, 4, and 5.
In Rule 2: 17, 23, 29, and 35.

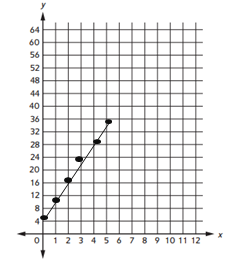
Question 5.
Use the graph to answer the questions below. Use the formula to check your answers.
a. When the in number is 8, what is the out number? ___________
b. When y is 64, about how much is x? About __________

Answer:
5a = 53.
5b = 10.

Explanation:
In the above-given question,
given that,
The In number is 8.
8 x 6 + 5 = 53.
48 + 5 = 53.
x x 6 + 5 = 5.
4 + 60 = x.
x = 64.

Practice
Solve. Show your work on the back of this page.
Question 6.
3 \(\frac{1}{5}\) ∗ 2 \(\frac{2}{3}\) = ________

Answer:
3 \(\frac{1}{5}\) ∗ 2 \(\frac{2}{3}\) =128/15.

Explanation:
In the above-given question,
given that,
3 \(\frac{1}{5}\) ∗ 2 \(\frac{2}{3}\).
3(1/5) x 2 (2/3).
3 x 5 = 15.
15 + 1/5 = 16/5.
2 x 3 = 6.
6 + 2/3 = 8/3.
lcm of 3 and 5 = 15.
16 x 3 = 48.
8 x 5 = 40.
80 + 48 = 128/15.

Question 7.
8 \(\frac{1}{2}\) ∗ 12 = _________

Answer:
8 \(\frac{1}{2}\) ∗ 12 = 204/2.

Explanation:
In the above-given question,
given that,
8 x 2 = 16.
16 + 1/2 = 17/2.
17/2 x 12 = 204/2.

Question 8.
9 ∗ 5 \(\frac{1}{7}\) = __________

Answer:
9 ∗ 5 \(\frac{1}{7}\) = 324/7.

Explanation:
In the above-given question,
given that,
7 x 5 = 35.
35 + 1/7 = 36/7.
36/7 x 9 = 324/7.