Everyday Mathematics 4th Grade Answer Key Unit 8 Fraction Operations; Applications
Everyday Math Grade 4 Home Link 8.1 Answer Key
Multistep Number Stories
The fourth-grade students in Mr. Kennedy’s class are investigating energy and motion. Students worked in teams to build two machines: a car that is propelled by a mousetrap and a boat that is propelled by balloons. Today the teams are competing to see which cars and boats go farthest.
Each car or boat gets 3 trials. The total distance from all 3 trials is used to determine which car or boat went farthest. Solve the number stories to help Mr. Kennedy’s class compare the machines made by various teams.
Question .1
Team A’s car went 173 cm on the first trial, 206 cm on the second trial, and 245 cm on the third trial. Team B’s car went 217 cm on each of the three trials.
Which car went the farthest overall? ____
How much farther did it go? ____
Answer:
Distance travelled by Team A car in first trial = 173 cm
Distance travelled by Team A car in second trial = 206 cm
Distance travelled by Team A car in third trial = 245 cm
Total Distance travelled by Team A car 3 trials = 173 + 206 + 245 = 624 cm
Distance travelled by Team B car in each trial = 217 cm
Total Distance travelled by Team B car 3 trials = 217 + 217 + 217 = 651 cm
651 cm > 624 cm
Team B car went the farthest overall .
Distance More covered by Team B car than Team A car = 651 – 624 = 27 cm .
Therefore the farther distance it went is 27 cms
Question 2.
Team A’s boat went 130 cm in all. Team B’s boat went the same distance on all 3 trials and lost to Team A’s boat by 7 cm.
How far did Team B’s boat go on each trial? ____
Answer:
Distance travelled by Team A’s boat in all trials= 130 cm .
Distance travelled by Team B’s boat in each trial = x
Distance travelled by Team B’s boat in all trials = 3x cms .
Team B is lost by 7 cms that means distance travelled by Team B + 7cms = Distance travelled by Team A .
3x + 7 = 130
3x = 130 – 7
3x = 123
x = 41 cms
Therefore, Distance travelled by Team B’s boat in each trial = 41 cms .
Question 3.
Team D’s car went the same distance on each of its trials. Team C’s car went exactly 1 cm farther in each trial than Team D’s car. Team C’s car went 543 cm in all.
How far did Team D’s cargo on each trial? ___
Answer :
Distance travelled by Team D car in each trial = x
Distance travelled by Team D car in 3 trials = 3x
Distance travelled by Team C car in each trial = 1 cm farther in each trial than Team D’s car. = x + 1.
Distance travelled by Team C car in 3 trials = 3 ( x + 1 ) = 3x + 3 .
Distance travelled by Team C car in 3 trials = 543 .
3x + 3 = 543 .
3x = 543 – 3
3x = 540 .
x = 180 cms.
Therefore, Distance travelled by Team D car in each trial = x = 180 cms .
Practice
Question 4.
5,624 ÷ 8 = ____
Answer:
5,624 ÷ 8 = 703
Explanation :
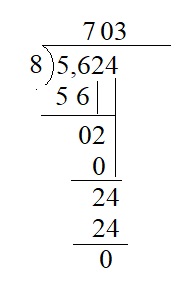
Question 5.
8,500 ÷ 3 = ___
Answer :
8,500 ÷ 3 = 2833 remainder 1
Explanation :
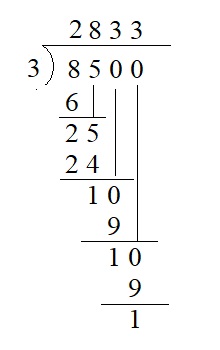
Question 6.
![]()
Answer:
9,207 ÷ 4 = 2301 remainder 3
Explanation :
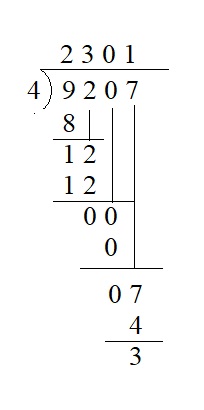
Question 7.
![]()
Answer:
3,578 ÷ 5 = 715 remainder 3
Explanation :
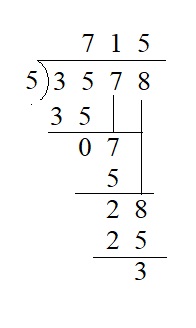
Everyday Math Grade 4 Home Link 8.2 Answer Key
Finding Unknown Angle Measures
Find the missing angle measures. For each problem, write an equation with a letter for the unknown to show how you found your answer.
Question 1.
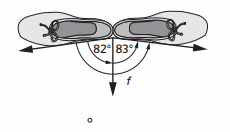
f = ___
Equation: ____
Answer:
f = 165 °
Equation :
82 ° + 83 ° = f
165 ° = f .
Question 2.
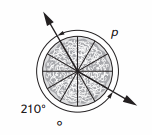
p = ___
Equation: ____
Answer:
The given figure is circle . the Total angle = 360°
the total angle = 210 ° + p = 360 °
Equation:
210 ° + p = 360 °
p = 360 ° – 210 °
p = 150°
Question 3.
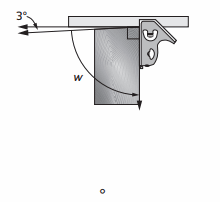
w = ___
Equation: ____
Answer:
The angle formed in the above figure is right angle = 90 °
Equation :
3 ° + w = 90 °
w = 90 ° – 3 °
w = 87 °
Question 4.

l = ___
Equation: ____
Answer:
The angle forward in a straight line.
Total angle = 180 ° .
Equation :
I + 75 ° = 180 °
I = 180 ° – 75 °
I = 105 °
Question 5.
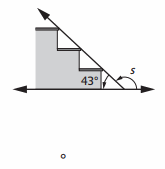
s = ___
Equation: ____
Answer:
The angle forward in a straight line.
Total angle = 180 ° .
Equation :
s + 43 ° = 180 °
s = 180 ° – 43 °
s = 137 °
Question 6.
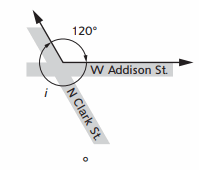
i = ___
Equation: ____
Answer:
The given figure is circle . the Total angle = 360°
the total angle = 120 ° + i = 360 °
Equation:
120 ° + i = 360 °
i = 360 ° – 120 °
i = 240°
Practice
Question 7.
\(\frac{1}{3}\) + \(\frac{2}{3}\) + \(\frac{2}{3}\) = ___
Answer:
\(\frac{1}{3}\) + \(\frac{2}{3}\) + \(\frac{2}{3}\)
All denominators are equal so add directly .
= \(\frac{5}{3}\) = 1\(\frac{2}{3}\)
Question 8.
\(\frac{1}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) = ____
Answer:
\(\frac{1}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) = \(\frac{7}{4}\) = 1\(\frac{3}{4}\)
Question 9.
\(\frac{4}{5}\) + \(\frac{4}{5}\) + \(\frac{3}{5}\) = ____
Answer:
\(\frac{4}{5}\) + \(\frac{4}{5}\) + \(\frac{3}{5}\) = \(\frac{11}{5}\) = 2\(\frac{1}{5}\)
Question 10.
\(\frac{5}{12}\) + \(\frac{3}{12}\) + \(\frac{7}{12}\) = ___
Answer:
\(\frac{5}{12}\) + \(\frac{3}{12}\) + \(\frac{7}{12}\) = \(\frac{15}{12}\) = 1\(\frac{3}{12}\)
Everyday Math Grade 4 Home Link 8.3 Answer Key
Finding Pattern-Block Measures
Molly is using pattern blocks to find angle measures of other pattern blocks. She knows that the measure of the small angle of a white rhombus is 30°.
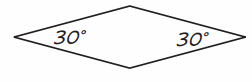
Question 1.
Molly fills an angle of the green triangle with the small angles of white rhombuses. What is the measure of the triangle’s angle? Explain how you know.
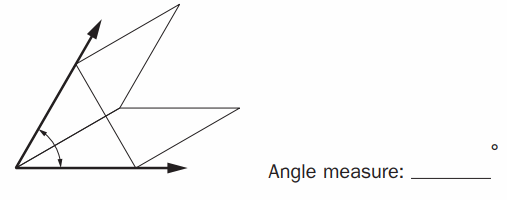
Answer:
Given Angle of small angles of white Rhombus = 30°
Angle formed in the above figure is by two small white rhombuses.
Angle formed = 30 ° + 30 ° = 60 ° .
Therefore, Angle Measure = 60 °
Question 2.
Molly fills a red trapezoid’s large angle with angles of the green triangle. What is the measure of the red trapezoid’s large angle? Explain how you know.
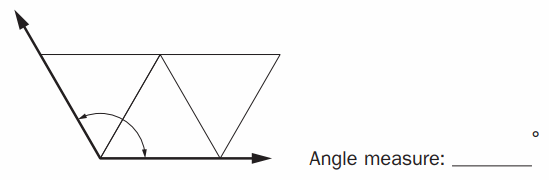
Answer :
Angle of the green triangle = 60 ° .
Angle formed by two green triangles .
Angle Measure of the red trapezoid’s large angle = 60 ° + 60 ° = 120 °
Therefore, Angle Measure of the red trapezoid’s large angle = 120 °
Practice
Question 3.
5,588 ∗ 3 = ____
Answer:
5,588 ∗ 3 = 16764
Explanation :
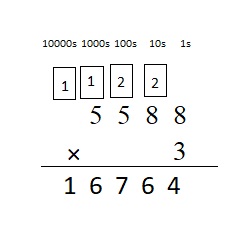
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 3.
8 × 3 = 24 = 2 ten + 4 ones
Write 4 in the ones column and carry 1 ten to tens place.
Step III: Multiply the digit at the tens place by 3.
8 × 3 = 24 tens
24 + 2 (carried) = 26 tens = 2 hundreds + 6 ten
Write 6 in ten place and carry 2 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 3.
5 hundred × 3 = 15 hundreds
15 hundreds + 2 hundreds (carried) = 1 thousands + 7 hundreds
Write 7 in hundreds place and carry 1 thousands to thousands place.
Step V: Multiply the digit at thousands place by 3.
5 thousands × 3 = 15 thousands
Write 5 in thousands place and carry 1 ten thousands to ten thousands place.
Question 4.
9,037 ∗ 5 = ___
Answer:
9,037 ∗ 5 = 45,185
Explanation :
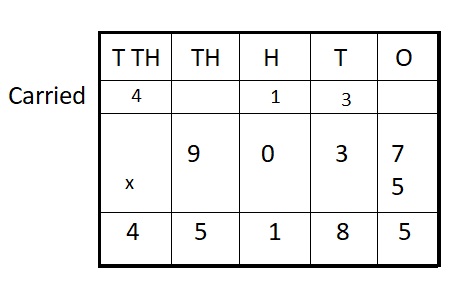
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 5.
7 × 5 = 35 = 3 ten + 5 ones
Write 5 in the ones column and carry 3 ten to tens place.
Step III: Multiply the digit at the tens place by 5.
3 × 5 = 15 tens
15 + 3 (carried) = 18 tens = 1 hundreds + 8 ten
Write 8 in ten place and carry 1 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 5
0 hundred × 5 = 0 hundreds
0 hundreds + 1 hundreds (carried) = 1 hundreds
Write 1 in hundreds place .
Step V: Multiply the digit at thousands place by 5.
9 thousands × 5 = 45 thousands
Write 5 in thousands place and carry 4 ten thousands to ten thousands place.
Question 5.
52 ∗ 94 = ___
Answer:
52 ∗ 94 = 4,888
Explanation :
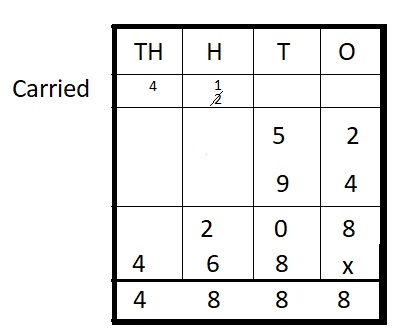
Step I: Arrange the numbers vertically.
Step II: Multiply 52 by 4 ones
52 × 4 = 208
Step III: Multiply 52 by 9 tens
52 × 90 = 4680
Step IV: Add
208 + 4680 = 4888
Question 6.
83 ∗ 77 = ___
Answer:
83 ∗ 77 = 6,391
Explanation :
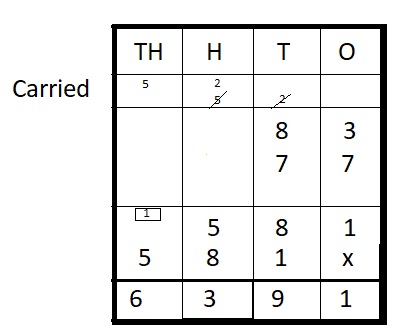
Step I: Arrange the numbers vertically.
Step II: Multiply 83 by 7 ones
83 × 7 = 581
Step III: Multiply 83 by 7 tens
83 × 70 = 5810
Step IV: Add
581 + 5810 = 6391
Everyday Math Grade 4 Home Link 8.4 Answer Key
Line Symmetry
Use a straightedge to draw the lines of symmetry on each shape.
Question 1.
Draw 2 lines of symmetry.
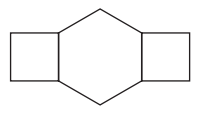
Answer:
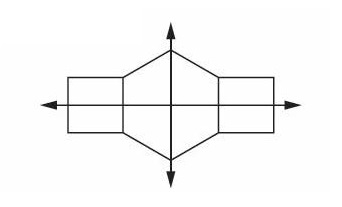
Explanation :
Something is symmetrical when it is the same on both sides. A shape has symmetry if a central dividing line (a mirror line) can be drawn on it, to show that both sides of the shape are exactly the same.
Question 2.
Draw 6 lines of symmetry
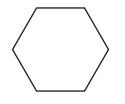
Answer:
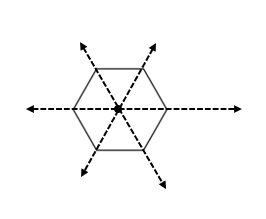
6 symmetrical lines are drawn from centre and 6 identical shapes are formed .
Explanation :
Something is symmetrical when it is the same on both sides. A shape has symmetry if a central dividing line (a mirror line) can be drawn on it, to show that both sides of the shape are exactly the same.
Question 3.
Draw 1 line of symmetry.
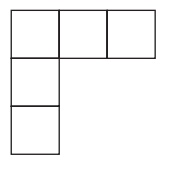
Answer:
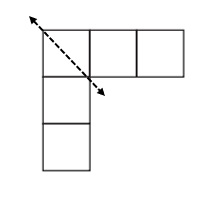
1 symmetrical lines is drawn and 2 identical shapes are formed .
Explanation :
Something is symmetrical when it is the same on both sides. A shape has symmetry if a central dividing line (a mirror line) can be drawn on it, to show that both sides of the shape are exactly the same.
Question 4.
Draw 3 lines of symmetry.
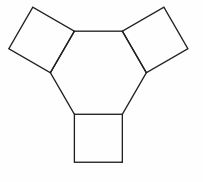
Answer:
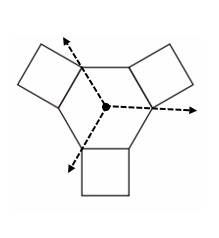
3 symmetrical lines is drawn from the centre and 3 identical shapes are formed .
Explanation :
Something is symmetrical when it is the same on both sides. A shape has symmetry if a central dividing line (a mirror line) can be drawn on it, to show that both sides of the shape are exactly the same.
Question 5.
How many lines of symmetry does this shape have? ___
Draw the line(s) of symmetry.
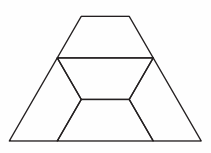
Answer:
Number of lines of symmetry for above shape = 1.
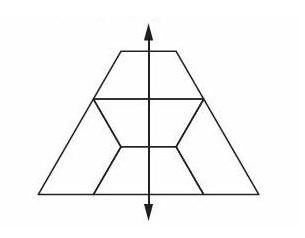
1 symmetrical lines is drawn and 2 identical shapes are formed .
Explanation :
Something is symmetrical when it is the same on both sides. A shape has symmetry if a central dividing line (a mirror line) can be drawn on it, to show that both sides of the shape are exactly the same.
Question 6.
Draw your own shape. Show the lines of symmetry. Be sure your shape includes at least 1 right angle.
Answer:
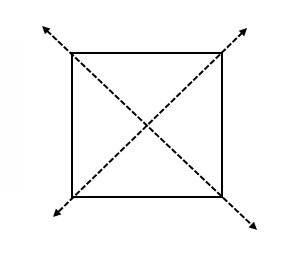
2 symmetrical lines is drawn and 4 identical shapes are formed .
Explanation :
Something is symmetrical when it is the same on both sides. A shape has symmetry if a central dividing line (a mirror line) can be drawn on it, to show that both sides of the shape are exactly the same.
Practice
Question 7.
6 ∗ \(\frac{5}{6}\) = ___
Answer:
6 ∗ \(\frac{5}{6}\) = 5
Question 8.
3 ∗ \(\frac{3}{8}\) = ___
Answer :
3 ∗ \(\frac{3}{8}\) = \(\frac{9}{8}\) = 1\(\frac{1}{8}\)
Question 9.
4 ∗ \(\frac{7}{10}\) = ___
Answer:
4 ∗ \(\frac{7}{10}\) = 2 ∗ \(\frac{7}{5}\) = \(\frac{14}{5}\) = 2\(\frac{4}{5}\)
Question 10.
6 * \(\frac{4}{12}\) = ___
Answer:
6 * \(\frac{4}{12}\) = 1 * \(\frac{4}{2}\) = \(\frac{2}{1}\) = 2
Everyday Math Grade 4 Home Link 8.5 Answer Key
Designing a Bookcase
Nicholas is building a bookcase. To help with the design, he measured the height
of each of his books to the nearest \(\frac{1}{8}\) inch. His measurements are given below.
6\(\frac{1}{2}\), 9\(\frac{1}{4}\), 7\(\frac{1}{8}\), 7\(\frac{1}{2}\), 8, 6\(\frac{7}{8}\), 9\(\frac{1}{4}\), 9\(\frac{1}{4}\), 9\(\frac{1}{4}\), 9\(\frac{1}{4}\), 9\(\frac{1}{4}\), 8\(\frac{1}{4}\), 8, 8\(\frac{1}{4}\), 8\(\frac{3}{8}\)
6\(\frac{1}{2}\), 7\(\frac{1}{8}\), 9, 6\(\frac{7}{8}\), 7\(\frac{1}{2}\), 8, 8\(\frac{1}{4}\), 9\(\frac{1}{4}\), 6\(\frac{7}{8}\), 6\(\frac{7}{8}\), 8\(\frac{1}{4}\), 8\(\frac{1}{4}\), 8\(\frac{1}{4}\)
Plot the data set on the line plot below
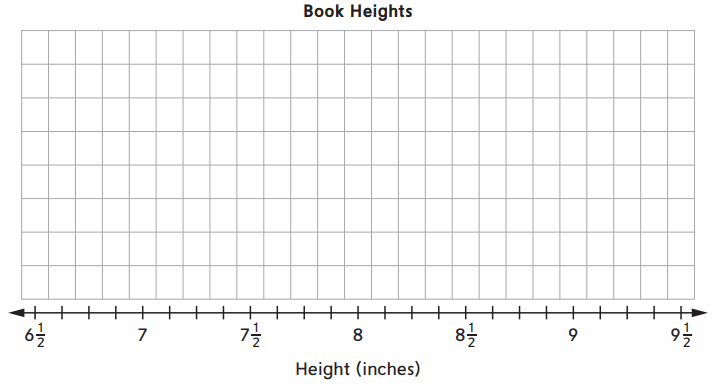
Use the completed line plot to answer the questions below.
Answer :
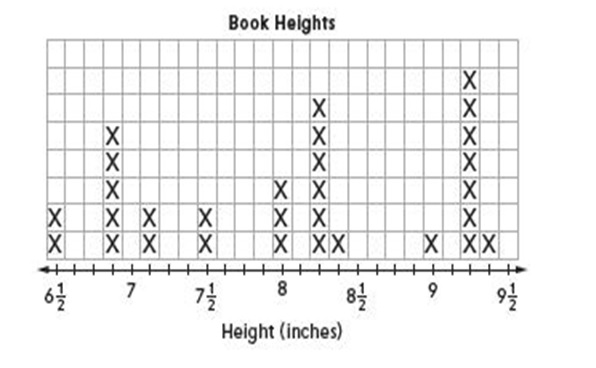
Question 1.
What is the difference in height between the tallest and shortest books? __ in.
Answer:
Height of tallest book = 9\(\frac{3}{8}\) inches
Height of the shortest book = 6\(\frac{1}{2}\) inches
The difference in height between the tallest and shortest books = 9\(\frac{3}{8}\) – 6\(\frac{1}{2}\) = \(\frac{75}{8}\)– \(\frac{13}{2}\) =\(\frac{75}{8}\)– \(\frac{52}{8}\) = \(\frac{23}{8}\)= 2\(\frac{7}{8}\) .
Therefore, the difference in height between the tallest and shortest books = 2\(\frac{7}{8}\) inches
Question 2.
Nicholas wants the space between the shelves to be \(\frac{7}{8}\) inch taller than his tallest book.
a. How far apart should he make the shelves? ___ in.
b. If the thickness of the wood he uses for the shelves is \(\frac{5}{8}\) inch, what will be the total height of each shelf? (Hint: The total height is the thickness of one piece of wood plus the distance between shelves.) __ in.
Answer :
a. Height of tallest book = 9\(\frac{3}{8}\) = \(\frac{75}{8}\) inches
the space between the shelves to be \(\frac{7}{8}\) inch
Height of the shelves to apart = \(\frac{75}{8}\) + \(\frac{7}{8}\) = \(\frac{82}{8}\) = \(\frac{41}{4}\) inches .
Practice
Question 3.
8,207 ÷ 7 → ___
Answer:
8,207 ÷ 7 → 1172 + 3 remainder
Explanation :
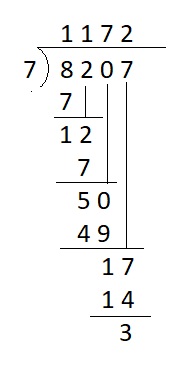
Question 4.
7,109 ÷ 8 → ___
Answer:
7,109 ÷ 8 → 888 + 5 remainder
Explanation :
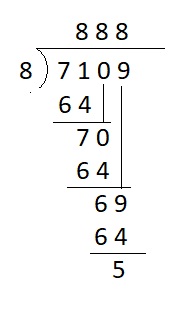
Everyday Math Grade 4 Home Link 8.6 Answer Key
Perimeters and Missing Measures
Use a formula to find the perimeter of each rectangle. Show your work in the space provided.
Question 1.
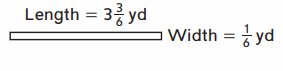
Perimeter: ___ yd
Answer:
Length of the Rectangle = 3\(\frac{3}{6}\) = \(\frac{21}{6}\) yd
Width of the rectangle = \(\frac{1}{6}\) yd
Perimeter of a Rectangle = 2 ( length + width ) = 2 ( \(\frac{21}{6}\) + \(\frac{1}{6}\) ) = 2 ( \(\frac{22}{6}\) ) = \(\frac{22}{3}\) yds .
Therefore, Perimeter of a Rectangle =\(\frac{22}{3}\) yds .
Question 2.
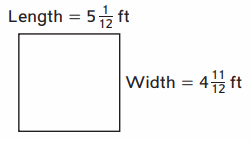
Perimeter: __ ft
Answer:
Length of the Rectangle = 5\(\frac{1}{12}\) = \(\frac{61}{12}\) ft
Width of the rectangle = 4\(\frac{11}{12}\) ft = \(\frac{59}{12}\) ft
Perimeter of a Rectangle = 2 ( length + width ) = 2 ( \(\frac{61}{12}\) + \(\frac{59}{12}\) ) = 2 ( \(\frac{120}{12}\) ) = 2 ( 10 ) = 20 ft .
Therefore, Perimeter of a Rectangle = 20 ft .
Question 3.
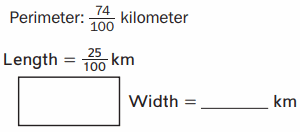
Answer:
Perimeter of a Rectangle = \(\frac{74}{100}\) kms
Length of the Rectangle = \(\frac{25}{100}\) km
Width of the Rectangle = W
Perimeter of a Rectangle = 2 ( length + width )
=> \(\frac{74}{100}\) = 2 ( \(\frac{25}{100}\) + W )
=> \(\frac{74}{100}\) = \(\frac{50}{100}\) + 2W
=> \(\frac{74}{100}\) – \(\frac{50}{100}\) = 2W
=> \(\frac{24}{100}\) = 2W
=> W = \(\frac{24}{200}\)
=> W = \(\frac{3}{25}\) km .
Therefore,Width of a Rectangle = \(\frac{3}{25}\) km
Question 4.
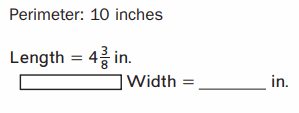
Answer:
Perimeter of a Rectangle = 10 in
Length of the Rectangle = 4\(\frac{3}{8}\) = \(\frac{35}{8}\) in
Width of the Rectangle = W
Perimeter of a Rectangle = 2 ( length + width )
=> 10 = 2 ( \(\frac{35}{8}\) + W )
=> 10 = \(\frac{35}{8}\)+ 2W
=> \(\frac{80}{8}\) – \(\frac{35}{8}\) = 2W
=> \(\frac{45}{8}\) = 2W
=> W = \(\frac{45}{16}\) = 2\(\frac{13}{16}\) in
Therefore,Width of a Rectangle = 2\(\frac{13}{16}\) in
Question 5.
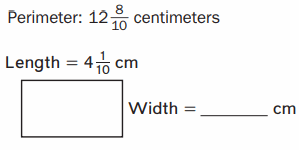
Answer:
Perimeter of a Rectangle = 12\(\frac{8}{10}\) = \(\frac{128}{10}\) cm
Length of the Rectangle = 4\(\frac{1}{10}\) = \(\frac{41}{10}\) cm
Width of the Rectangle = W
Perimeter of a Rectangle = 2 ( length + width )
=> \(\frac{128}{10}\) = 2 ( \(\frac{41}{10}\) + W )
=> \(\frac{128}{10}\) = \(\frac{82}{10}\) + 2W
=> \(\frac{128}{10}\) – \(\frac{82}{10}[/latex = 2W
=> [latex]\frac{46}{10}\) = 2W
=> W = \(\frac{46}{20}\)
=> W = \(\frac{23}{10}\) cm .
Therefore,Width of a Rectangle = \(\frac{23}{10}\) cm
Try this
Question 6.
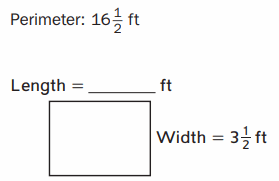
Answer:
Perimeter of a Rectangle = 16\(\frac{1}{2}\) = \(\frac{33}{2}\) ft
Width of the rectangle = 3\(\frac{1}{2}\) ft = \(\frac{7}{2}\) ft
Length of the Rectangle = L
Perimeter of a Rectangle = 2 ( length + width )
=> \(\frac{33}{2}\) = 2 ( L + \(\frac{7}{2}\) )
=> \(\frac{33}{2}\) = 2L + \(\frac{14}{2}\)
=> \(\frac{33}{2}\) – \(\frac{14}{2}\) = 2L
=> \(\frac{19}{2}\) = 2L
=> L = \(\frac{19}{4}\) = 4\(\frac{3}{4}\) ft
Therefore, Perimeter of a Rectangle = 4\(\frac{3}{4}\) ft .
Practice
Question 7.
2 ∗ \(\frac{2}{3}\) = ___
Answer:
2 ∗ \(\frac{2}{3}\) = 1 \(\frac{1}{3}\)
Explanation :
2 ∗ \(\frac{2}{3}\) = \(\frac{4}{3}\) =1 \(\frac{1}{3}\)
Question 8.
5 ∗ \(\frac{3}{4}\) = __
Answer:
5 ∗ \(\frac{3}{4}\) = 3\(\frac{3}{4}\)
Explanation :
5 ∗ \(\frac{3}{4}\) = \(\frac{15}{4}\) = 3\(\frac{3}{4}\)
Question 9.
9 ∗ \(\frac{4}{5}\) = __
Answer:
9 ∗ \(\frac{4}{5}\) = 7\(\frac{1}{5}\)
Explanation :
9 ∗ \(\frac{4}{5}\) = \(\frac{36}{5}\) = 7\(\frac{1}{5}\)
Question 10.
8 ∗ \(\frac{6}{12}\) = ___
Answer:
8 ∗ \(\frac{6}{12}\) = 4
Explanation :
8 ∗ \(\frac{6}{12}\) = 8 ∗ \(\frac{1}{2}\) = 4 ∗ \(\frac{1}{1}\) = 4
Everyday Math Grade 4 Home Link 8.7 Answer Key
Decimal Number Stories
Solve each number story. Write your answer as a decimal. Show how you found your answer.
Question 1.
An Olympic men’s shot put weighs 7.26 kilograms. An Olympic women’s shot put weighs 4 kilograms. How much more does the men’s shot put weigh than the women’s shot put?
__ kilograms
Answer:
Weight of the Olympic men’s shot put = 7.26 kilograms
Weight of the Olympic women’s shot put = 4 kilograms
More Weight of men’s shot put weigh than the women’s shot put = 7.26 – 4.00 = 3.26 kilograms .
Therefore, More Weight of men’s shot put weigh than the women’s shot put = 3.26 kilograms .
Question 2.
The recipe for homemade glue calls for 0.5 liter of skim milk, 0.09 liter of vinegar, and 0.06 liter of water. When you combine the ingredients, how much liquid will you have?
__ liter
Answer:
Quantity of skim milk = 0.5 liter
Quantity of vinegar = 0.09 liter
Quantity of water = 0.06 liter
Quantity of liquid formed = 0.5 + 0.09 + 0.06 = 0.65 liters .
Therefore, Quantity of liquid formed = 0.65 liters .
Question 3.
Ben cut a piece of string 11.4 cm long. Then he cut 3.6 cm off of it. How long is the string now?
__ cm
Answer:
Length of the string = 11.4 cm long
Quantity of Length cut off = 3.6 cm
Quantity of length of the string left off = 11.4 – 3.6 = 7.8 cm .
Therefore, length of the string now = 7.8 cm .
Try This
Question 4.
What is the answer to Problem 3 in millimeters? __ millimeters
Answer:
length of string now = 7.8 cm
1cm = 10 m
multiply cm value into 10 to get the quantity in millimeters .
7.8 cm = 78 millimeters .
Therefore, length of string now = 7.8 cm = 78 millimeters .
Practice
Question 5.
3,579 ∗ 4 = __
Answer:
3,579 ∗ 4 = 14,316
Explanation :
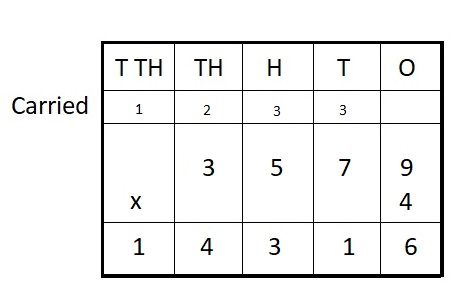
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 4.
9 × 4 = 36 = 3 ten + 6 ones
Write 6 in the ones column and carry 3 ten to tens place.
Step III: Multiply the digit at the tens place by 4.
7 × 4 = 28 tens
28 + 3 (carried) = 31 tens = 3 hundreds + 1 ten
Write 1 in ten place and carry 3 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 4
5 hundred × 4 = 20 hundreds
20 hundreds + 3 hundreds (carried) = 23 hundreds = 2 thousands + 3 hundreds
Write 3 in hundreds place carry 2 thousands to thousands place.
Step V: Multiply the digit at thousands place by 4.
3 thousands × 4 = 12 thousands
12 + 2 (carried) = 14 thousands = 1 ten thousands + 4 thousands
Write 4 in thousands place and carry 1 ten thousands to ten thousands place.
Question 6.
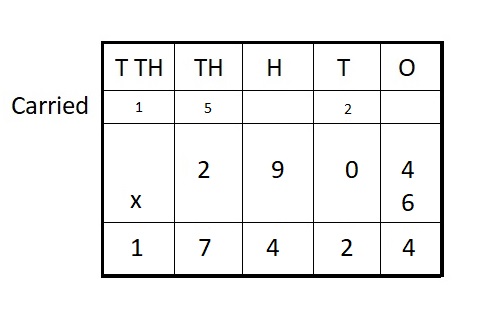
2,904 ∗ 6 = __
Answer:
2,904 ∗ 6 = 17,424
Question 7.
36 ∗ 56 = ___
Answer:
36 ∗ 56 = 2,116
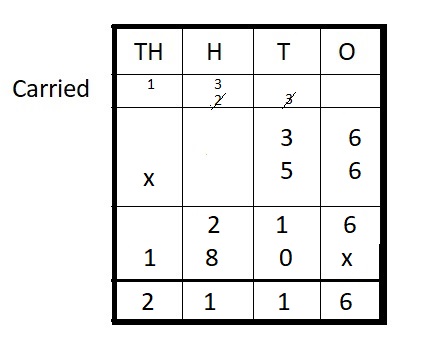
Step I: Arrange the numbers vertically.
Step II: Multiply 36 by 6 ones
36 × 6 = 216
Step III: Multiply 36 by 50 tens
36 × 50 = 1800
Step IV: Add
216 + 1800 = 2116
Question 8.
47 ∗ 72 = __
Answer:
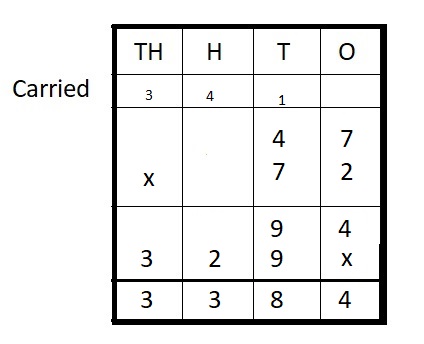
Step I: Arrange the numbers vertically.
Step II: Multiply 47 by 2 ones
47 × 2 = 94
Step III: Multiply 36 by 50 tens
47 × 70 = 3290
Step IV: Add
94 + 3290 = 3384
Everyday Math Grade 4 Home Link 8.8 Answer Key
Area and Perimeter
Solve the problems below.
Question 1.
The Murphy family bought two rectangular dog beds for their pets. Fluffy’s bed was 3 feet by 1\(\frac{9}{12}\) feet. Pete’s bed was 4 feet by 2\(\frac{4}{12}\) feet.
a. How much more area does Pete’s bed have than Fluffy’s?
Answer: ____ square feet
Length of the Fluffy’s bed = 3 feet
Width of Fluffy’s bed = 1\(\frac{9}{12}\) = \(\frac{21}{12}\) feet .
Area of the fluffy’s bed = length × Width = 3 × \(\frac{21}{12}\) = \(\frac{63}{12}\) feet .
Length of the pete’s bed = 4 feet
Width of pete’s bed = 2\(\frac{4}{12}\) = \(\frac{28}{12}\) feet .
Area of the pete’s bed = length × Width = 4 × \(\frac{28}{12}\) = \(\frac{112}{12}\) feet .
Quantity of more Area of Pete’s bed have than Fluffy’s = \(\frac{112}{12}\) – \(\frac{63}{12}\) = \(\frac{49}{12}\) feet .
Therefore, Quantity of more Area of Pete’s bed have than Fluffy’s = \(\frac{49}{12}\) feet
b. What is the perimeter of Pete’s bed?
Answer: ___ feet
Length of the pete’s bed = 4 feet
Width of pete’s bed = 2\(\frac{4}{12}\) = \(\frac{28}{12}\) feet .
Perimeter of the pete’s bed = 2 ( l + w ) = 2 ( 4 + \(\frac{28}{12}\) ) = 2 ( \(\frac{48}{12}\) + \(\frac{28}{12}\) ) = 2 ( \(\frac{76}{12}\) ) = \(\frac{76}{6}\) = \(\frac{38}{3}\) feet .
Therefore, Perimeter of the pete’s bed = \(\frac{38}{3}\) feet
Question 2.
The Cho family bought two rectangular cat beds for their cats. George’s bed is 2 feet by 1\(\frac{2}{12}\) feet. Sammie’s bed is 2 feet by 1\(\frac{7}{12}\) feet.
a. What is the total area of these two beds? Answer: __ square feet
b. What is the perimeter of George’s bed? Answer: ___ feet
Answer :
a .
Length of George’s bed = 2 feet
Width of George’s bed = 1\(\frac{2}{12}\) = \(\frac{14}{12}\) Feet .
Area of George’s bed = length × Width = 2 × \(\frac{14}{12}\) = \(\frac{28}{12}\) square Feet .
Length of Sammie’s bed = 2 feet
Width of Sammie’s bed = 1\(\frac{7}{12}\) = \(\frac{19}{12}\) Feet .
Area of Sammie’s bed = length × Width = 2 × \(\frac{19}{12}\) = \(\frac{38}{12}\) square Feet .
Total Area of two beds = \(\frac{28}{12}\) + \(\frac{38}{12}\) = \(\frac{66}{12}\) = \(\frac{11}{2}\) square feet.
Therefore,Total Area of two beds = \(\frac{11}{2}\) square feet .
b.
Length of George’s bed = 2 feet
Width of George’s bed = 1\(\frac{2}{12}\) = \(\frac{14}{12}\) Feet .
Perimeter of George’s bed = 2 ( l + w ) = 2 ( 2 + \(\frac{14}{12}\) ) = 2 ( \(\frac{24}{12}\) + \(\frac{14}{12}\) ) = 2 ( \(\frac{38}{24}\) ) = \(\frac{38}{12}\) = \(\frac{19}{6}\) feet .
Therefore, Perimeter of George’s bed = \(\frac{19}{6}\) feet
Question 3.
Perimeter: 12\(\frac{2}{10}\) inches
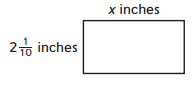
Area: __ square inches
Answer:
Perimeter of the Rectangle = 12\(\frac{2}{10}\) = \(\frac{122}{10}\) inches
Length of the Rectangle = x inches .
Width of the Rectangle = 2\(\frac{1}{10}\) = \(\frac{21}{10}\) inches
Perimeter of the Rectangle = 2 ( l + b) = 2 ( x + \(\frac{21}{10}\) )
=> \(\frac{122}{10}\) = 2x + \(\frac{42}{10}\)
=>\(\frac{122}{10}\) – \(\frac{42}{10}\) = 2x
=> \(\frac{80}{10}\) = 2x
=> 8 = 2x
=> x = 4 inches.
Therefore, length of the Rectangle = 4 inches .
Question 4.
Area: 9\(\frac{3}{8}\) square feet
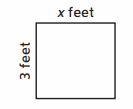
Width: ___ feet
Answer :
Area of the Rectangle = 9\(\frac{3}{8}\) = \(\frac{75}{8}\) square feet
Length of Rectangle = x feet.
Width of the Rectangle = 3 feet .
Area of the Rectangle = length × Width = x × 3
=> \(\frac{75}{8}\) = x × 3
=> \(\frac{75}{8 × 3 }\) = x
= > x = \(\frac{75}{24}\) = \(\frac{25}{8}\) feet
Therefore, Length of Rectangle = x = \(\frac{25}{8}\) feet .
Practice
Question 5.
\(\frac{5}{6}\) – \(\frac{1}{6}\) = ___
Answer:
\(\frac{5}{6}\) – \(\frac{1}{6}\) = \(\frac{4}{6}\) = \(\frac{2}{3}\)
Question 6.
\(\frac{8}{8}\) – \(\frac{3}{8}\) = __
Answer:
\(\frac{8}{8}\) – \(\frac{3}{8}\) = \(\frac{5}{8}\)
Question 7.
\(\frac{9}{10}\) – \(\frac{5}{10}\) = __
Answer:
\(\frac{9}{10}\) – \(\frac{5}{10}\) = \(\frac{4}{10}\) = \(\frac{2}{5}\)
Question 8.
\(\frac{11}{12}\) – \(\frac{5}{12}\) = __
Answer:
\(\frac{11}{12}\) – \(\frac{5}{12}\) = \(\frac{6}{12}\) = \(\frac{1}{2}\)
Everyday Math Grade 4 Home Link 8.9 Answer Key
Using Doghouse Dimensions
Dan and Diane’s Doghouse Dynasty builds doghouses to order. They can change the length and width for doghouses, but they always build them to have the same height. Solve the number stories about doghouses built to certain widths and lengths based on the information given in the table. Use drawings or equations to show how you solved each problem.
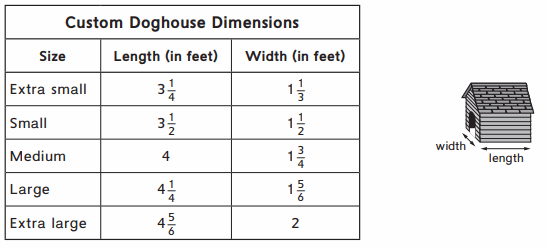
Question 1.
Mrs. Swift ordered 3 medium-size doghouses. What will their combined width be? __ feet
Answer:
Length of the Medium size dog house = 4 feet
Width of the Medium size dog house = 1\(\frac{3}{4}\) = \(\frac{7}{4}\) .
Width of 3 medium size dog house = 3 × \(\frac{7}{4}\) = \(\frac{21}{4}\) = 5\(\frac{1}{4}\) .
Therefore, The Combined width = 5\(\frac{1}{4}\) feet .
Question 2.
Kisa’s Kennel has a space that is 18 feet wide in which they want to place doghouses side by side. If they order 5 small and 4 medium doghouses, will they all fit in the space? ___
Answer :
Width of the space = 18 feet .
Width of small dog house = 1\(\frac{1}{2}\) = \(\frac{3}{2}\) feet .
Width of 5 small dog houses = 5 × \(\frac{3}{2}\) = \(\frac{15}{2}\) feet = 7.5 feet
Width of the Medium size dog house = 1\(\frac{3}{4}\) = \(\frac{7}{4}\) .
Width of the 4 Medium size dog houses = 4 × \(\frac{7}{4}\) = 7 .
Total width of 5 small and 4 medium doghouses = 7.5 + 7 = 14.5 feet
14.5 < 18 feet so, Yes, they will fit in the 18 feet space.
Practice
Question 3.
2 ∗ \(\frac{3}{6}\) = ___
Answer :
2 ∗ \(\frac{3}{6}\) = 1 ∗ \(\frac{3}{3}\) = 1
Question 4.
5 ∗ \(\frac{7}{10}\) = __
Answer:
5 ∗ \(\frac{7}{10}\) = 1 ∗ \(\frac{7}{2}\) = \(\frac{7}{2}\) = 3\(\frac{1}{2}\)
Question 5.
9 ∗ \(\frac{6}{100}\) = ___
Answer:
9 ∗ \(\frac{6}{100}\) = \(\frac{54}{100}\)
Question 6.
7 ∗ \(\frac{8}{12}\) = __
Answer:
7 ∗ \(\frac{8}{12}\) = 7 ∗ \(\frac{2}{3}\) = \(\frac{14}{3}\)
Everyday Math Grade 4 Home Link 8.10 Answer Key
Liquid Measurement and Fractions
Complete the “What’s My Rule?” tables and state the rules.
Question 1.
Rule: __
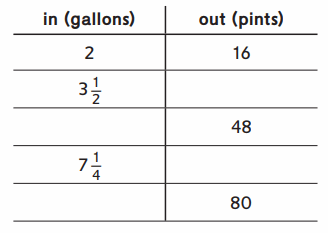
Answer:
Rule: Out(pints) is 8 times in(gallons) .
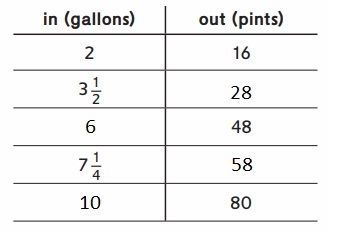
Explanation :
=> in = 3\(\frac{1}{2}\) = \(\frac{7}{2}\)
out = 8 × \(\frac{7}{2}\) = 4 × \(\frac{7}{1}\) = 28 .
=> out = 48 .
in = \(\frac{out}{8}\) = \(\frac{48}{8}\) = 6 .
=> in = 7\(\frac{1}{4}\) = \(\frac{29}{4}\)
out = 8 × \(\frac{29}{4}\) = 2 × \(\frac{29}{1}\) = 58 .
=> out = 80 .
in = \(\frac{out}{8}\) = \(\frac{80}{8}\) = 10 .
Question 2.
Rule: __
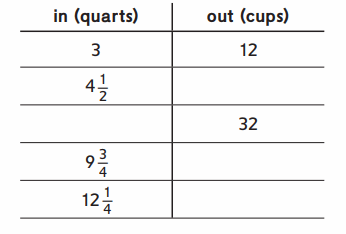
Answer:
Rule: 4 times in (quarts) is the out ( cups) .
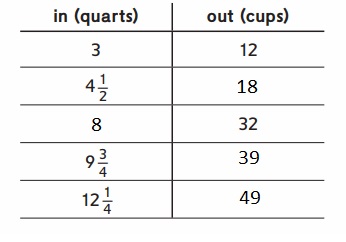
Explanation :
=> in = 4\(\frac{1}{2}\) = \(\frac{9}{2}\)
out = 4 × \(\frac{9}{2}\) = 2 × \(\frac{9}{1}\) = 18 .
=> out = 32
in = \(\frac{out}{4}\) = \(\frac{32}{4}\) = 8 .
=> in = 4\(\frac{1}{2}\) = \(\frac{9}{2}\)
out = 4 × \(\frac{9}{2}\) = 2 × \(\frac{9}{1}\) = 18 .
=> in = 9\(\frac{3}{4}\) = \(\frac{39}{4}\)
out = 4 × \(\frac{39}{4}\) = 1 × \(\frac{39}{1}\) = 39 .
=> in = 12\(\frac{1}{4}\) = \(\frac{49}{4}\)
out = 4 × \(\frac{49}{4}\) = 1 × \(\frac{49}{1}\) = 49 .
Use this recipe for a Creamsicle Smoothie to solve the problems below. \(\frac{3}{4}\) cup orange juice 4 fluid ounces cold water 1 cup vanilla ice cream
Combine all ingredients.
Question 3.
a. Will this recipe fit in a glass that holds 24 fluid ounces? _____
Explain your thinking.
Answer:
Yes, the Sample will fill .
Explanation :
The total amount of all combined ingredients is 18 fluid ounces, so, the smoothie will fit in the 24-fluid ounce glass .
b. About how many more cup(s) of smoothie could fit in the glass? ___ cup(s)
Answer:
glass Quantity = 24 ounces .
Ingredients Quantity = 18 ounces .
More Quantity can fill = 24 – 18 ounces = 6 ounces .
6 ounces = \(\frac{3}{4}\) cup
c. Frank wants to triple the recipe. How much of each ingredient will he need?
__ orange juice
__ cold water
___ vanilla ice cream
Answer:
\(\frac{3}{4}\) cup orange juice , 4 fluid ounces cold water 1 cup vanilla ice cream
triple the given quantities by multiplying into 3 , we get.
\(\frac{9}{4}\) cup orange juice , 12 fluid ounces cold water 3 cup vanilla ice cream
d. After tripling the recipe, how much smoothie will Frank have? __ fluid ounces
Answer:
The total amount of all combined ingredients is 18 fluid ounces
After tripling the Quantity is
The total amount of all combined ingredients after tripling= 3 ×18 fluid ounces = 54 ounces.
Practice
Question 4.
3,560 ÷ 3 → __
Answer:
3,560 ÷ 3 → 1186 + 2 Remainder .
Explanation :
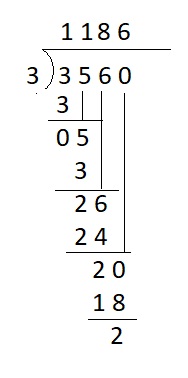
Question 5.
9,295 ÷ 5 → __
Answer:
9,295 ÷ 5 → 1,859
Explanation :
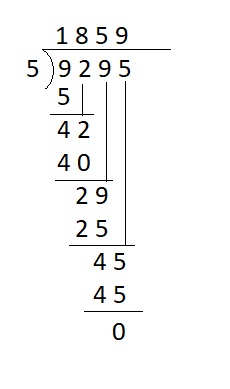
Question 6.
![]()
Answer:
![]() = 1174 + 2 Remainder .
= 1174 + 2 Remainder .
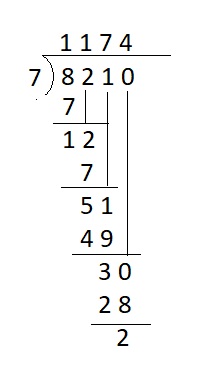
Question 7.
![]()
Answer:
![]() = 519
= 519
Explanation :
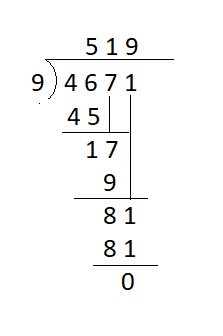
Everyday Math Grade 4 Home Link 8.11 Answer Key
Planning a Cookout
The Whispering Lakes Neighborhood Association is having a hamburger cookout. Each family can choose whether to order the hamburgers or bring their own. Use the information in the table to solve the number stories. Use drawings, tables, or equations to show what you did.
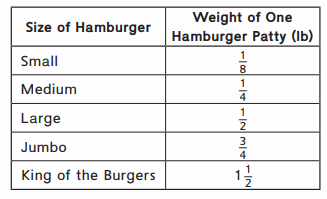
Question 1.
a. What is the combined weight of 1 of each size hamburger? __ pounds
Answer:
Weight of Small size Hamburger = \(\frac{1}{8}\)
Weight of Medium size Hamburger = \(\frac{1}{4}\)
Weight of Large size Hamburger = \(\frac{1}{2}\)
Weight of Jumbo size Hamburger = \(\frac{3}{4}\)
Weight of king of the burgers of one = 1\(\frac{1}{2}\) = \(\frac{3}{2}\) .
Total Weight of all burgers = \(\frac{1}{8}\) + \(\frac{1}{4}\) + \(\frac{1}{2}\) + \(\frac{3}{4}\) + \(\frac{3}{2}\) = \(\frac{1}{8}\) + \(\frac{4}{4}\) + \(\frac{4}{2}\) = \(\frac{1}{8}\) + \(\frac{8}{8}\) + \(\frac{16}{8}\) = \(\frac{25}{8}\) = 3\(\frac{1}{8}\) .
Therefore, Total Weight of all hamburgers = 3\(\frac{1}{8}\) pounds .
b. How many ounces is that? __ ounces
Answer:
50 ounces .
Explanation :
\(\frac{25}{8}\) pounds = ? ounces .
1 pound = 16 ounces .
Multiply the pounds value into 16 to get in ounces .
=> \(\frac{25}{8}\) × 16 = \(\frac{25}{1}\) × 2 = 50 ounces .
c. Mrs. Ward found 80- ounce packages of hamburger on sale. If she needs to make 2 of each size hamburger, how many packages of meat will she need to buy?
__ packages
Answer:
2 packages .
Explanation :
1 of each size hamburgers weights = 50 ounces .
2 of each size hamburgers weights = 2 × 50 ounces = 100 ounces .
total weight of 1 packages = 80 ounces.
80< 100 ounces.
Therefore, we require 2 packages of meat .
Question 2.
The Finch family ordered 2 small hamburgers, 1 medium hamburger, and 1 jumbo hamburger. How many pounds of hamburger meat does the neighborhood association need to buy for this family?
__ pounds
Answer:
Weight of Small size Hamburger = \(\frac{1}{8}\)
Weight of Medium size Hamburger = \(\frac{1}{4}\)
Weight of Jumbo size Hamburger = \(\frac{3}{4}\)
Total pounds of hamburger ordered = \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{4}\) + \(\frac{3}{4}\) = \(\frac{2}{8}\) + \(\frac{4}{4}\) = \(\frac{1}{4}\) + \(\frac{4}{4}\) = \(\frac{5}{4}\) = 1 \(\frac{1}{4}\) pounds .
Therefore, pounds of hamburger meat does the neighborhood association need to buy for this family = 1 \(\frac{1}{4}\) pounds
Practice
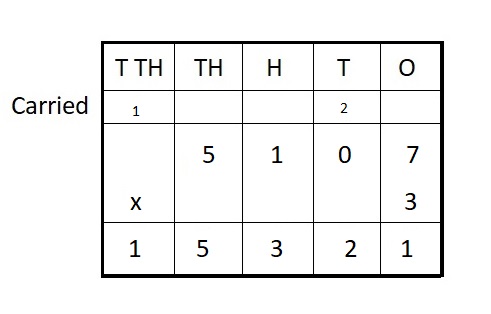
Question 3.
5,107 ∗ 3 = __
Answer :
5,107 ∗ 3 = 15,321
Explanation :
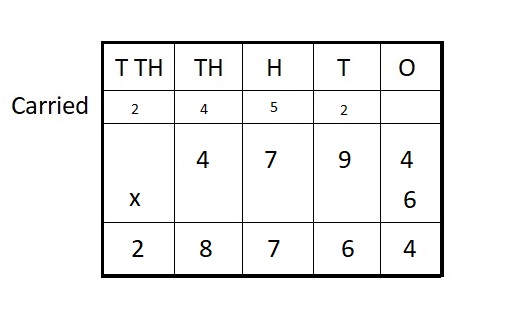
Question 4.
4,794 ∗ 6 = __
Answer:
4,794 ∗ 6 = 28,764
Explanation :
Question 5.
74 ∗ 29 = __
Answer:
74 ∗ 29 = 2,146
Explanation :
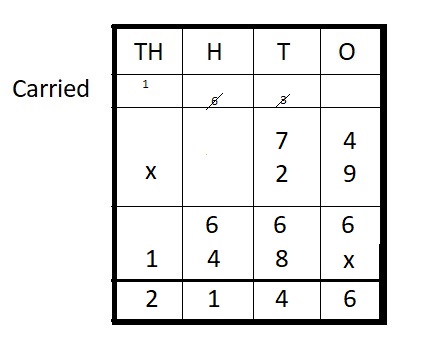
Step I: Arrange the numbers vertically.
Step II: Multiply 74 by 9 ones
74 × 9 = 666
Step III: Multiply 74 by 2 tens
74 × 20 = 1480
Step IV: Add
666 + 1480 = 2146
Question 6.
93 ∗ 48 = __
Answer:
93 ∗ 48 =4,464
Explanation :
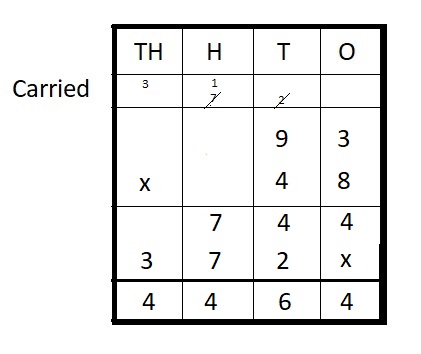
Step I: Arrange the numbers vertically.
Step II: Multiply 93 by 8 ones
93 × 8 = 744
Step III: Multiply 93 by 4 tens
93 × 40 = 3720
Step IV: Add
744 + 3720 = 4464
Everyday Math Grade 4 Home Link 8.12 Answer Key
Number-Tile Computations
Cut out the 0–9 number tiles at the bottom of the page. Use them to help you solve the problems. Each of the 20 tiles can only be used once.
Question 1.
Use odd-numbered tiles 1, 3, 5, 7, and 9 to make the largest sum.
Answer:
add 973 and 51 gives largest sum 1024 .
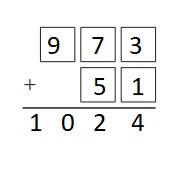
Question 2.
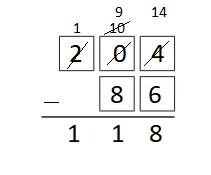
Use even-numbered tiles 0, 2, 4, 6, and 8 to make the smallest difference.
Answer:
Subtract 204 – 86 we get difference as 118
Question 3.
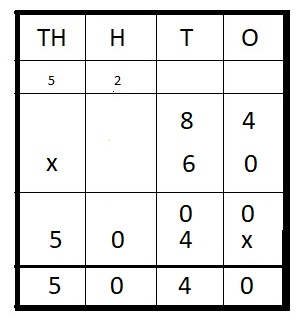
Use number tiles 0, 4, 6, and 8 to make the largest product.
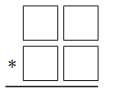
Answer:
Multiply 84 and 60 we get largest product = 5,040.
Question 4.
Use number tiles 1, 2, 5, and 7 to make the smallest whole-number quotient. The answer may have a remainder.

Answer:
125 divided by 7 = 17 + 6 Remainder .
Question 5.
Answer the following questions using only the unused tiles and any operation. Write number sentences to show your work.
a. What is the largest answer you can find?

Answer :
3 and 9 numbers are unused
To get largest number we need to multiply those number 9 × 3 = 27
b. What is the smallest answer you can find?

Answer :
3 and 9 numbers are unused
To get smallest number we need to divide those number 9 ÷ 3 = 3
Practice
Question 6.
4\(\frac{3}{5}\) + 3\(\frac{4}{5}\) = ____
Answer:
4\(\frac{3}{5}\) + 3\(\frac{4}{5}\) = \(\frac{23}{5}\) + \(\frac{19}{5}\) = \(\frac{42}{5}\) = 8\(\frac{2}{5}\)
Question 7.
1\(\frac{5}{8}\) + 3\(\frac{5}{8}\) = __
Answer:
1\(\frac{5}{8}\) + 3\(\frac{5}{8}\) = \(\frac{13}{8}\) + \(\frac{29}{8}\) = \(\frac{42}{8}\) = 5\(\frac{2}{8}\)
Question 8.
2\(\frac{9}{12}\) + 4\(\frac{5}{12}\) = __
Answer:
2\(\frac{9}{12}\) + 4\(\frac{5}{12}\) = \(\frac{33}{12}\) + \(\frac{53}{12}\) = \(\frac{86}{12}\) = \(\frac{43}{6}\) = 7\(\frac{1}{6}\)
Question 9.
5\(\frac{89}{100}\) + 5\(\frac{92}{100}\) = __
Answer:
5\(\frac{89}{100}\) + 5\(\frac{92}{100}\) = \(\frac{589}{100}\) + \(\frac{592}{100}\) = \(\frac{1181}{100}\) = 11\(\frac{81}{100}\)
Everyday Math Grade 4 Home Link 8.13 Answer Key
Many Names for Numbers
Write five names in each box below. Use as many different kinds of numbers (such as whole numbers, fractions, decimals) and different operations (+, -, ∗, ÷) as you can.
Question 1.

Answer:

Question 2.

Answer:

Make up your own name-collection boxes.
Question 3.

Answer:

Question 4.

Answer:

Practice
Question 5.
5\(\frac{1}{4}\) – 1\(\frac{3}{4}\) = __
Answer:
5\(\frac{1}{4}\) – 1\(\frac{3}{4}\) = \(\frac{21}{4}\) – \(\frac{7}{4}\) = \(\frac{14}{4}\) = \(\frac{7}{2}\) = 3\(\frac{1}{2}\)
Question 6.
4\(\frac{3}{10}\) – 2\(\frac{7}{10}\) = __
Answer:
4\(\frac{3}{10}\) – 2\(\frac{7}{10}\) = \(\frac{43}{10}\) – \(\frac{27}{10}\) = \(\frac{16}{10}\) = \(\frac{8}{5}\) = 1\(\frac{3}{5}\)
Question 7.
6\(\frac{7}{12}\) – 3\(\frac{11}{12}\) = __
Answer:
6\(\frac{7}{12}\) – 3\(\frac{11}{12}\) = \(\frac{79}{12}\) – \(\frac{47}{12}\) = \(\frac{32}{12}\) = \(\frac{8}{3}\) = 2\(\frac{2}{3}\) .
Question 8.
8\(\frac{1}{6}\) – 4\(\frac{5}{6}\) = __
Answer:
8\(\frac{1}{6}\) – 4\(\frac{5}{6}\) = \(\frac{49}{6}\) – \(\frac{29}{6}\) = \(\frac{20}{6}\) = \(\frac{10}{3}\) = 3\(\frac{1}{3}\) .