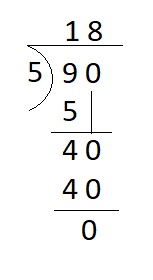Everyday Mathematics 4th Grade Answer Key Unit 6 Division; Angles

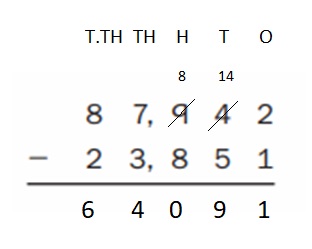
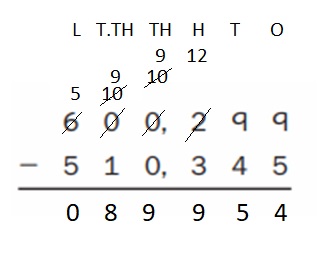
Everyday Math Grade 4 Home Link 6.1 Answer Key

Solving Extended Division Facts

Write a basic division fact and an extended division fact for each Fact Triangle.

Question 1.

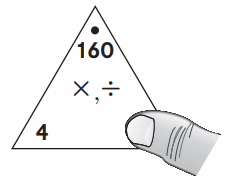
Basic fact: 16 ÷ 4 = ___
Extended fact: 160 ÷ 4 = ____
Answer :
Basic fact: 16 ÷ 4 = 4
Extended fact: 160 ÷ 4 = 40

Question 2.

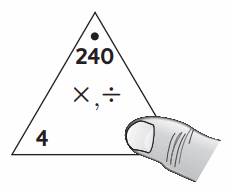
Basic fact: ___
Extended fact: ___
Answer :
Basic fact: 24 ÷ 4 = 6
Extended fact:  240 ÷ 4 = 60

Solve.

Question 3.
a. 25 ÷ 5 ____
b. 250 ÷ 5 = ___
c. 2,500 ÷ 5 = ___
d. 250 ÷ 50 = ___
Answer:
a. 25 ÷ 5 = 5
b. 250 ÷ 5 = 50
c. 2,500 ÷ 5 = 500
d. 250 ÷ 50 = 5

Question 4.
a. 36 ÷ 4 = ___
b. 360 ÷ 4 = ___
c. 3,600 ÷ 4 = ___
d. 360 ÷ 40 = ___
Answer:
a. 36 ÷ 4 = 9
b. 360 ÷ 4 = 90
c. 3,600 ÷ 4 = 900
d. 360 ÷ 40 = 9

Question 5.
a. 18 ÷ 9 = ___
b. 180 ÷ 9 = ___
c. 1,800 ÷ 9 = ___
d. 180 ÷ 90 = ___
Answer:
a. 18 ÷ 9 = 2
b. 180 ÷ 9 = 20
c. 1,800 ÷ 9 = 200
d. 180 ÷ 90 = 2

Question 6.
a. 42 / 7 = ___
b. 420 / 7 = __
c. 4,200 / 7 = __
d. 420 / 70 = ___
Answer:
a. 42 / 7 = 6
b. 420 / 7 = 60
c. 4,200 / 7 = 600
d. 420 / 70 = 6

Practice

Question 7.
456 ∗ 5 = ___
Answer:
456 ∗ 5 = 2,280
Explanation :

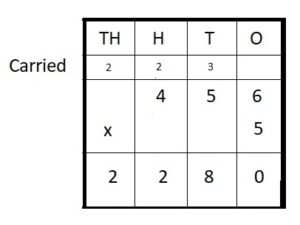
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 5.
6 × 5 = 30 = 3 ten + 0 ones
Write 0 in the ones column and carry 3 ten to tens place.
Step III: Multiply the digit at the tens place by 5.
5 × 5 = 25 tens
25 + 3 (carried) = 28 tens = 2 hundreds + 8 ten
Write 8 in ten place and carry 2 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 5.
4 hundred × 5 = 20 hundreds
20 hundreds + 2 hundreds (carried) = 2 thousands + 2 hundreds
Write 2 in hundreds place and carry 1 thousands to thousands place.

Question 8.
720 ∗ 8 = __
Answer:
720 ∗ 8 = 5,760
Explanation :

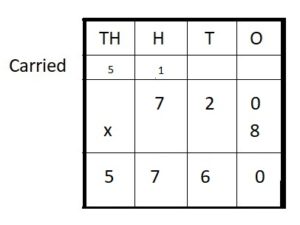
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 8.
0 × 8 = 0
Write 0 in the ones column
Step III: Multiply the digit at the tens place by 8.
2 × 8 = 16 tens
16 tens = 1 hundreds + 6 ten
Write 6 in ten place and carry 1 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 8.
7 hundred × 8 = 56 hundreds
56 hundreds + 1 hundreds (carried) = 5 thousands + 7 hundreds
Write 7 in hundreds place and carry 5 thousands to thousands place.

Question 9.
905 ∗ 7 = ___
Answer:
905 ∗ 7 = 6,335
Explanation :

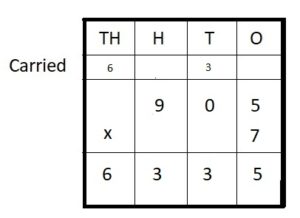
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 7.
5 × 7 = 35 = 3 ten + 5 ones
Write 5 in the ones column and carry 3 ten to tens place.
Step III: Multiply the digit at the tens place by 7.
0 × 7 = 0 tens
Write 0 in tens place
Step IV: Multiply the digit at hundreds place by 7.
9 hundred × 7 = 63 hundreds
63 hundreds = 6 thousands + 3 hundreds
Write 3 in hundreds place and carry 6 thousands to thousands place.

Everyday Math Grade 4 Home Link 6.2 Answer Key

Finding the Unknown Side Length

Solve.

Question 1.

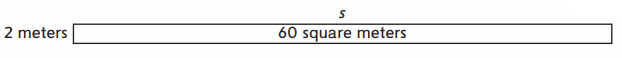
How long is the unknown side s? _____
Equation with unknown: ____
Answer: ___ meters
Area of the Rectangle = 60 square meters.
Width of the rectangle = 2 meters
Length of the Rectangle = s meters .
Area of the Rectangle = length × Width
60 = s × 2
s = 60 ÷ 2
s = 30 meters .

Question 2.

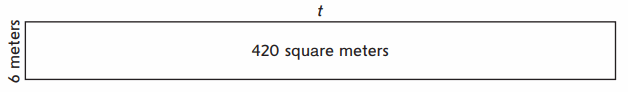
What is the length of the unknown side t?
Equation with unknown: _____
Answer: ___ meters
Answer:
Area of the Rectangle = 420 square meters.
Width of the rectangle = 6 meters
Length of the Rectangle = t meters .
Area of the Rectangle = length × Width
420 = t × 6
s = 420 ÷ 6
s = 70 meters .

Question 3.
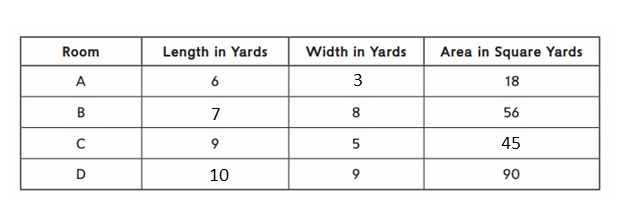
Fill in the unknown information about some rectangular rooms in a museum.

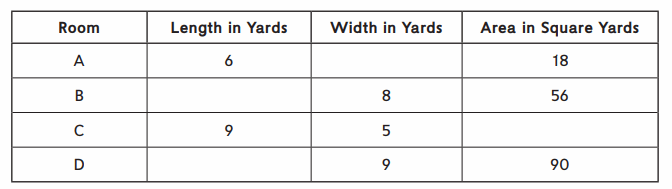
Answer:

Explanation :
Room A:
Area of the Room A = 18 square yards.
Width of the rectangle = w yards
Length of the Rectangle = 6 yards.
Area of the Rectangle = length × Width
18 = 6 × w
w = 18 ÷ 6
w = 3 yards.
Room B:
Area of the Rectangle = 56 square yards.
Width of the rectangle = 8 yards.
Length of the Rectangle = L yards.
Area of the Rectangle = length × Width
56 = L × 8
L = 56 ÷ 8
L = 7 yards.
Room C:
Width of the rectangle = 5 yards.
Length of the Rectangle = 9 yards.
Area of the Rectangle = length × Width = 9 × 5 = 45 square yards.
Room D :
Area of the Rectangle = 90 square yards.
Width of the rectangle = 9 yards.
Length of the Rectangle = L yards.
Area of the Rectangle = length × Width
90 = L × 9
L = 90 ÷ 9
L = 10 yards.

Question 4.
A store is rectangular in shape with an area of 2,700 square feet. It has a length of 90 feet. How wide is it?
Equation with unknown: ____
Answer: ___ feet
Answer:
Area of the Rectangular store = 2700 square feet.
Width of the rectangle = w feet
Length of the Rectangle = 90 feet
Area of the Rectangle = length × Width
2700 = 90 × w
w = 2700 ÷ 90
w = 30 feet.
Therefore, Width of the rectangle = w feet = 30 feet .

Practice

Question 5.
420 ÷ 7 = __
Answer:
420 ÷ 7 = 60
Explanation :

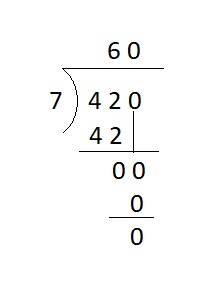
Question 6.
___ = 3,600 / 6
Answer:
600 = 3,600 / 6
Explanation :

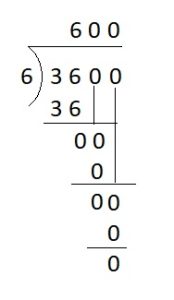
Question 7.
5,400 ÷ 90 = ___
Answer:
5,400 ÷ 90 = 60
Explanation :

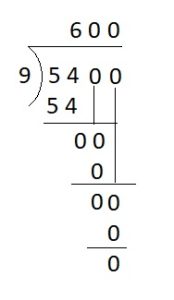
Everyday Math Grade 4 Home Link 6.3 Answer Key

Solving Division Number Stories

Fill in the lists of multiples to help you, if needed.

Question 1.
Rosario sells bicycle wheels in packages of 2. If a store orders 46 wheels, how many packages will she send?
20 [2s] = Number model with unknown: ____
21 [2s] = Answer: __ packages
22 [2s] = Number model with answer: _____
23 [2s] = _____
24 [2s] = _____
25 [2s] = _____
Answer:
Number of wheels in one package = 2 .
Number of wheels order = 46 wheels.
Numbers of packages required for 46 wheels = Total Wheels ÷ number of wheels in one package = 46 ÷ 2 = 23 packages
Therefore, Number of packages required for 46 wheels = 23 packages .
20 [2s] = 20 ×  2 = 40 wheels.
21 [2s] = 21 ×  2 = 42 wheels.
22 [2s] = 22 ×  2 = 44 wheels.
23 [2s] = 23 ×  2 = 46 wheels.
24 [2s] = 24 ×  2 = 48 wheels.
25 [2s] = 25 ×  2 = 50 wheels.

Question 2.
Doug is placing apples in bags for a picnic. He can fit 6 apples in a bag. If he has 92 apples, how many bags will he need?
10 [6s] = ___ Number model with unknown: ____
11 [6s] = __ Answer: __ bags
12 [6s] = ___ Number model with answer: ____
13 [6s] = _____
14 [6s] = ___
15 [6s] = _____
16 [6s] = ______
17 [6s] = _____
18 [6s] = ____
Answer :
Number apples in a bag = 6 apples
Total number of apples = 92 .
Number of bags required for 92 apples = Total apples ÷ Number of apples in one bag = 92 ÷ 6 = 15\(\frac{2}{6}\) Bags.
10 [6s] = 10 ×  6 = 60 apples
11 [6s] = 11 ×  6 = 66 apples
12 [6s] = 12 ×  6 = 72 apples
13 [6s] = 13 ×  6 = 78 apples
14 [6s] = 14 ×  6 = 84 apples
15 [6s] = 15 ×  6 = 90 apples
16 [6s] = 16 ×  6 = 96 apples
17 [6s] = 17 ×  6 = 102 apples
18 [6s] =18 ×  6 = 108 apples

Practice

Question 3.
82 ∗ 10 = ___
Answer:
82 ∗ 10 = 820 .
Explanation :
Any multiplied by 10 the product will be added with single 0 on the left of the number .

Question 4.
___ = 25 ∗ 30
Answer:
750 =  25 ∗ 30
Explanation :

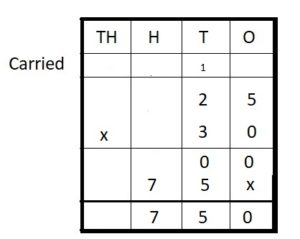
Step I: Arrange the numbers vertically.
Step II: Multiply 25 by 0 ones
25 × 0 = 00
Step III: Multiply 25 by 3 tens
25 × 30 = 750
Step IV: Add
0 + 750 = 750

Question 5.
333 ∗ 3 = ____
Answer:
333 ∗ 3 = 999
Explanation :

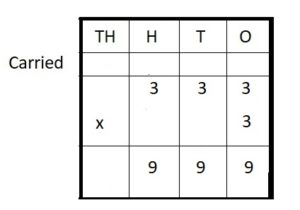
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 3.
3 × 3 = 9
Write 9 in the ones column
Step III: Multiply the digit at the tens place by 3.
3 × 3 = 9 tens
Write 9 in ten place
Step IV: Multiply the digit at hundreds place by 3.
3 hundred × 3 = 9 hundreds
Write 9 in hundreds place

Everyday Math Grade 4 Home Link 6.4 Answer Key

Partial-Quotients Division

Family Note In this lesson students are introduced to the partial-quotients method, in which a number is divided in a series of steps. The quotients for each step (called partial quotients) are added to give the final answer. For example, to divide 96 by 6, students use extended multiplication facts such as 6 ∗ 10 = 60 to find the partial quotient. Then with the remaining 36, they use an “easy”
multiplication fact, 6 ∗ 6, to finish solving the problem. These two partial quotients are added together, 10 + 6, to find the exact quotient of 16. So 96 ÷ 6 = 16.

Estimate. Write a number model with an unknown to represent the problem. Then solve using partial quotients.

Question 1.
Jordan has 3 Great Dane puppies. At 6 weeks old, their combined weight is 48 pounds. Assuming that they all weigh about the same amount, how much does each puppy weigh?
Estimate: ____
Number model with unknown: ____

Answer: ___ pound(s)
Number of Puppies = 3
Total Weight of puppies = 48 pounds.
Weight of 3 puppies is the same .
Weight of each puppy = total weight ÷ Total puppies = 48 ÷ 3 = (30 + 18 ) ÷ 3 = 10 + 6 = 16 pounds.
Therefore weight of each puppy = 16 pounds .
Estimate :
Number of Puppies = 3
Total Weight of puppies = 48 pounds. => 45 pounds
Weight of 3 puppies is the same .
Weight of each puppy = total weight ÷ Total puppies = 45 ÷ 3 = (30 + 15 ) ÷ 3 = 10 + 5 = 15 pounds.
Therefore weight of each puppy = 15 pounds . ( Estimation ) .

Question 2.
Four sisters love barrettes. They have a value pack that contains 92 barrettes. How many barrettes can each sister have if they share equally?
Estimate: ____
Number model with unknown ____
Answer: ___ barrette(s)
Number of sisters = 4
Total Number of Barrettes = 92
Number of Barrettes each sister gets = 92 ÷ 4 = 23 barrettes .
Estimate :
Number of sisters = 4
Total Number of Barrettes = 92 =>100
Number of Barrettes each sister gets = 100 ÷ 4 = (80 + 20 ) ÷ 4= 20 + 5 = 25 barrettes .

Practice

Name two equivalent fractions for each fraction give n.

Question 3.
\(\frac{1}{2}\) ____ ____
Answer:
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) .
Explanation :
Multiply both the numerator and denominator of a fraction by the same whole number. As long as you multiply both top and bottom of the fraction by the same number, you won’t change the value of the fraction, and you’ll create an equivalent fraction.

Question 4.
\(\frac{1}{3}\) ___ __
Answer:
\(\frac{1}{3}\) = \(\frac{2}{6}\) = \(\frac{3}{9}\)
Explanation :
Multiply both the numerator and denominator of a fraction by the same whole number. As long as you multiply both top and bottom of the fraction by the same number, you won’t change the value of the fraction, and you’ll create an equivalent fraction.

Question 5.
\(\frac{25}{10}\) __ ___
Answer:
\(\frac{25}{10}\) = \(\frac{50}{20}\) = \(\frac{75}{30}\)
Explanation :
Multiply both the numerator and denominator of a fraction by the same whole number. As long as you multiply both top and bottom of the fraction by the same number, you won’t change the value of the fraction, and you’ll create an equivalent fraction.

Question 6.
\(\frac{6}{8}\) __ ___
Answer:
\(\frac{6}{8}\) = \(\frac{12}{19}\) = \(\frac{18}{24}\)Explanation :
Multiply both the numerator and denominator of a fraction by the same whole number. As long as you multiply both top and bottom of the fraction by the same number, you won’t change the value of the fraction, and you’ll create an equivalent fraction.

Everyday Math Grade 4 Home Link 6.5 Answer Key

Assigning People to Buses

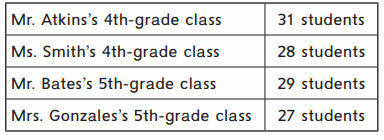
Mr. Atkins is organizing the 4th- and 5th-grade field trip to the science museum. He asked his students to help him figure out which students and teachers should go on each bus. The number of students in each class is shown in the table below:

Important information:

• 4 buses have been ordered.
• The maximum number of passengers is 30 per bus.
• Each bus must have 1 teacher.

Cary said he solved the problem this way:

Question 1.
What do the numbers in his sentence mean?
Answer:
Total Number of students = 31 + 28 + 29 + 27 = 115 .
Total Number of Buses = 4
Number of students in the bus = 28 .
remainder = 3 means 3 buses can have 1 more passenger divided equally .

Question 2.
Which students and teachers should go on each bus? Explain why.
Answer:
Total Number of students = 31 + 28 + 29 + 27 = 115 .
Total Number of Buses = 4
Number of students in the bus = 28 .
remainder = 3 means 3 buses can have 1 more passenger divided equally .
That means 3 buses have 29 passengers and 1 bus have 28 passengers.
Number of teachers = 4 that means each should have 1 teacher then.
3 buses will have 30 passengers and 1 bus will have 29 passengers .
Explanation :
Mr Atikin’s bus have 31 students that means when 1 teacher added total passengers will become 32 . that means he have 2 passengers extra . he puts that 2 passengers on Mrs.Gonzale’s bus .
In Gonzales’s bus number of students are 27 and and 1 teacher equal to 28 passengers then 2 passengers can fit in this bus .
In Smith’s bus number of students are 28 and and 1 teacher equal to 29 passengers
In Bate’s bus number of students are 29 and and 1 teacher equal to 30 passengers

Everyday Math Grade 4 Home Link 6.6 Answer Key

 

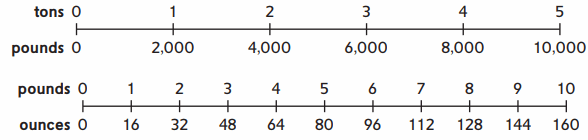
Use the measurement scales to help you solve the problems.

Question 1.

Answer:

Explanation :
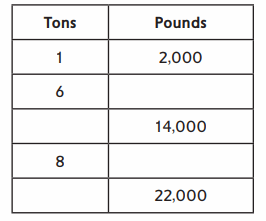
1 ton = 2,000 pounds
6 tons = 6 × 2,000 = 12,000 pounds .
7 tons = 7 × 2,000 = 14,000 pounds .
8 tons = 8 × 2,000 = 16,000 pounds .
11 tons = 11 × 2,000 = 22,000 pounds .

Question 2.

Answer:

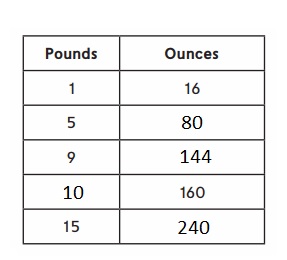
Explanation :
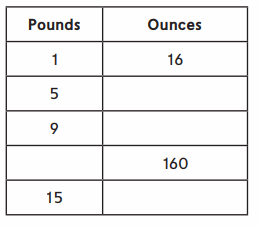
1 Pound = 16 ounces
5 Pounds = 5 × 16 = 80 ounces .
9 Pounds = 9 × 16 = 144 ounces .
10 Pounds = 10 × 16 = 160 ounces .
15 Pounds = 15 × 16 = 240 ounces .

Question 3.
The army chef is ordering food for the troops. She ordered 2 tons of rice, 1 ton of pasta, and 1 ton of flour. How many pounds of food did she order?
Answer: __ pound(s)
Answer:
Total Quantity ordered = 4 tons = 8,000 pounds .
Explanation :
Quantity of Rice = 2 tons
Quantity of  Pasta = 1 ton
Quantity of Flour = 1 ton
Total Quantity ordered = 2 + 1 + 1 = 4 tons.
1 ton = 2,000 pounds.
4 tons = 4 × 2,000 = 8,000 pounds .
Therefore, Total Quantity ordered = 4 tons = 8,000 pounds .

Question 4.
Potatoes come in 8-pound bags. How many ounces do 12 bags weigh?
Answer: ___ ounce(s)
Weight of 12 bags = 96 pounds = 1,536 ounces .
Explanation :
Weight of Potatoes of 1 bag = 8 pounds
Weight of 12 bags = 12 × 8 = 96 pounds .
1 pound = 16 ounces
96 pounds = 96 × 16 = ( 100 – 4 ) × 16 = 1600 – 64 = 1536 ounces .

Practice

Question 5.
\(\frac{4}{8}\) + \(\frac{3}{8}\) = ___
Answer:
\(\frac{4}{8}\) + \(\frac{3}{8}\) = \(\frac{7}{8}\)
Explanation :
\(\frac{4}{8}\) + \(\frac{3}{8}\) = \(\frac{7}{8}\)

Question 6.
__ = \(\frac{5}{8}\) – \(\frac{3}{8}\)
Answer:
\(\frac{5}{8}\) + \(\frac{3}{8}\) = 1
Explanation :
\(\frac{5}{8}\) + \(\frac{3}{8}\) = \(\frac{8}{8}\) = 1

Question 7.
__ = \(\frac{5}{10}\) + \(\frac{3}{100}\)
Answer:
\(\frac{53}{100}\)  = \(\frac{5}{10}\) + \(\frac{3}{100}\)
Explanation :
\(\frac{5}{10}\) + \(\frac{3}{100}\) = \(\frac{50}{100}\) + \(\frac{3}{100}\) = \(\frac{53}{100}\)

Question 8.
\(\frac{60}{100}\) + \(\frac{4}{10}\) = ___
Answer:
\(\frac{60}{100}\) + \(\frac{4}{10}\) = \(\frac{6}{10}\) + \(\frac{4}{10}\) = \(\frac{10}{10}\) = 1 .

Everyday Math Grade 4 Home Link 6.7 Answer Key

Partial Quotients

Estimate. Write a number model to represent the problem. Solve using partial quotients.

Question 1.
The carnival committee has 360 small prizes to distribute to 5 booths. How many prizes will each booth get?
Estimate: ____
Number model with unknown:
________
Answer: ___ prizes
How many prizes are left? __ prizes
Answer :
Number of booths = 5
Number of prizes  = 360
Number of prizes each booth get = total prizes ÷ number of booths = 360 ÷ 5 = ( 300 + 60 ) ÷ 5 = ( 300 ÷ 5 )+ ( 60 ÷ 5 ) = 60 + 12 = 72  prizes .
All prizes are divided equally to all 5 booths that is 72 prizes .
Estimate :
Number of booths = 5
Number of prizes  = 360 ==> 400
Number of prizes each booth get = total prizes ÷ number of booths = 400 ÷ 5 = ( 200 + 200 ) ÷ 5 = ( 200 ÷ 5 )+ ( 200 ÷ 5 ) = 40 + 40 = 80  prizes .

Question 2.
The mall needs a row of parking spaces. The length of the parking area is 2,711 feet. If each parking space is 9 feet wide, how many
spaces will there be?
Estimate: ___
Number model with unknown: ___

Answer: ___ spaces
How many feet are left over? ___ feet
Answer :
Length of the parking area = 2,711 feet
Width of parking area = 9 feet .
Number of spaces = 2,711 ÷ 9 = ( 2700 + 11 ) ÷ 9 = (2700 ÷ 9 ) + ( 11 ÷ 9 ) = 300 + 1 + 2 Remainder = 301 + 2 Remainder .
Estimate :
Length of the parking area = 2,711 feet ==> 2,700 feet
Width of parking area = 9 feet ==> 10 feet
Number of spaces = 2,700 ÷ 10 = ( 2000 + 700 ) ÷ 10 = (2000 ÷ 10 ) + ( 700 ÷ 10 ) = 200 + 70 = 270 spaces .

Solve using partial quotients. Show your work on the back of this page.

Question 3.
161 / 7 Estimate: ____ Answer: ____
Answer:
161 / 7 = 23 .
Estimate :
161 ==> 160
7 ==> 8
160 ÷ 8 = 20

Question 4.
576 / 4 Estimate: ___ Answer: ____
Answer:
576 / 4 = 144 .
Estimate :
576 ==> 600
4 ==> 4
600 ÷ 4 = 150

Practice

Put these decimals in order from least to greatest.

Question 5.
0.98, 0.34, 9.8, 0.08 ___, ___, ___, ___
Answer:
0.98, 0.34, 9.8, 0.08
Ascending order :
0.08 < 0.34 < 0.98 < 9.8
arranged from least to greatest .

Question 6.
0.11, 0.01, 0.10, 1.0 ___, __, __, __
Answer:
0.11, 0.01, 0.10, 1.0
Ascending order :
0.01 < 0.10 < 0.11 < 1.0
arranged from least to greatest .

Use <, >, or = to compare the decimals.

Question 7.
0.65 ___ 0.5
Answer:
0.65 > 0.5
Explanation :
When comparing decimals, start in the tenths place. The decimal with the biggest value there is greater. If they are the same, move to the hundredths place and compare these values. If the values are still the same keep moving to the right until you find one that is greater or until you find that they are equal.

Question 8.
37.9 ___ 37.96
Answer:
37.9 < 37.96
Explanation :
When comparing decimals, start in the tenths place. The decimal with the biggest value there is greater. If they are the same, move to the hundredths place and compare these values. If the values are still the same keep moving to the right until you find one that is greater or until you find that they are equal.

Everyday Math Grade 4 Home Link 6.8 Answer Key

Interpreting Remainders

Question 1.
Mrs. Patel brought a box of 124 strawberries to the party. She wants to divide the strawberries evenly among 8 people. How many
strawberries will each person get?
Number model with unknown:
Answer:
____ strawberries Number model with answer:
What did you do about the remainder? Circle the answer.
A. Ignored it
B. Reported it as a fraction
C. Rounded the answer up
Why? ________
Answer:
Total Number of Straw berries = 124 .
Number of people = 8 .
Number of straw berries each get =  124 ÷ 8 = (120 ÷ 8 ) + ( 4 ÷ 8 ) = 15 + \(\frac{1}{2}\) = 15\(\frac{1}{2}\).
124 ÷ 8 = 15 + 4 Remainder .
15 are divided equally for 8 people and 4 are left that means each person gets \(\frac{1}{2}\) strawberry .
Therefore each get 15\(\frac{1}{2}\) strawberries .
B . Reported it as fraction .
because 4 strawberries are cut into halves and distributed equally to 8 people .

Question 2.
Mr. Chew has a box of 250 pens. He asks Maurice to divide the pens into groups of 8. How manygroups can Maurice make?
Number model with unknown:
Answer:
_____ groups
Number model with answer:
What did you do about the remainder?
Circle the answer.
A. Ignored it
B. Reported it as a fraction
C. Rounded the answer up
Why? _____
Answer:
Total Number of pens = 250 .
Number of  pens for each group = 8
Number of groups  = 250 ÷ 8 = ( 240 + 10 ) ÷ 8 = ( 240 ÷ 8 ) + ( 10 ÷ 8 ) = 30 + 1 + 2 Remainder .
31 + 2 remainder.
that means groups are 31 and 2 are left .
A. Ignored it as 31 groups get 8 pens and 2 pens are left so, ignored .
2 cannot be given for a group as each contains 8 pens .

Practice

Order the fractions from smallest to largest.

Question 3.
\(\frac{3}{6}\), \(\frac{3}{3}\), \(\frac{3}{5}\), \(\frac{3}{8}\) __, __, __, __
Answer:
\(\frac{3}{6}\), \(\frac{3}{3}\), \(\frac{3}{5}\), \(\frac{3}{8}\)
lcm of 3,6 , 5 and 8 is 240
= \(\frac{120}{240}\), \(\frac{240}{240}\), \(\frac{144}{240}\), \(\frac{90}{240}\)
= \(\frac{90}{240}\) < \(\frac{120}{240}\) < \(\frac{144}{240}\) < \(\frac{240}{240}\)
\(\frac{3}{8}\) < \(\frac{3}{6}\) < \(\frac{3}{5}\) < \(\frac{3}{3}\)
Explanation :
You cannot compare the fractions directly because they have different denominators. You need to find a common denominator for the given fractions and then compare the numerator values . greater the numerator greater the fraction .

Question 4.
\(\frac{1}{4}\), \(\frac{1}{8}\), \(\frac{1}{2}\), \(\frac{1}{5}\), ___, ___, __, ___
Answer:
\(\frac{1}{4}\), \(\frac{1}{8}\), \(\frac{1}{2}\), \(\frac{1}{5}\)
lcm of 4, 8, 2 and 5 is 40 .
= \(\frac{10}{40}\), \(\frac{5}{40}\), \(\frac{20}{40}\), \(\frac{8}{40}\)
\(\frac{5}{40}\) < \(\frac{8}{40}\) < \(\frac{10}{40}\) < \(\frac{20}{40}\)
\(\frac{1}{8}\) < \(\frac{1}{5}\) < \(\frac{1}{4}\) < \(\frac{1}{2}\)
Explanation :
You cannot compare the fractions directly because they have different denominators. You need to find a common denominator for the given fractions and then compare the numerator values . greater the numerator greater the fraction .

Question 5.
\(\frac{2}{3}\), \(\frac{1}{2}\), \(\frac{6}{8}\), \(\frac{99}{100}\), __, ___, __, ___
Answer:
\(\frac{2}{3}\), \(\frac{1}{2}\), \(\frac{6}{8}\), \(\frac{99}{100}\)
lcm of 3, 2, 8, 100 = 600 .
= \(\frac{400}{600}\), \(\frac{300}{600}\), \(\frac{450}{600}\), \(\frac{594}{600}\)
\(\frac{300}{600}\) < \(\frac{400}{600}\) < \(\frac{450}{600}\) < \(\frac{594}{600}\)
\(\frac{1}{2}\) < \(\frac{2}{3}\) < \(\frac{6}{8}\) < \(\frac{99}{100}\)
Explanation :
You cannot compare the fractions directly because they have different denominators. You need to find a common denominator for the given fractions and then compare the numerator values . greater the numerator greater the fraction .

Question 6.
\(\frac{4}{5}\), \(\frac{81}{100}\), \(\frac{4}{6}\), \(\frac{2}{10}\) = __, __, __, __
Answer:
\(\frac{4}{5}\), \(\frac{81}{100}\), \(\frac{4}{6}\), \(\frac{2}{10}\)
\(\frac{4}{5}\), \(\frac{81}{100}\), \(\frac{2}{3}\), \(\frac{1}{5}\)
lcm of 5,100, 3 is 300
\(\frac{240}{300}\), \(\frac{243}{300}\), \(\frac{200}{300}\), \(\frac{60}{300}\)
\(\frac{60}{300}\)  < \(\frac{200}{300}\) < \(\frac{240}{300}\) < \(\frac{243}{300}\)
\(\frac{2}{10}\)  < \(\frac{4}{6}\) < \(\frac{4}{5}\) < \(\frac{81}{100}\)
Explanation :
You cannot compare the fractions directly because they have different denominators. You need to find a common denominator for the given fractions and then compare the numerator values . greater the numerator greater the fraction .

Everyday Math Grade 4 Home Link 6.9 Answer Key

Measuring Angles

Cut out the angle measurer and use a pencil to poke a hole through the center.
Label each angle acute, right, or obtuse.
Then use the angle measurer to measure each angle.

Question 1.

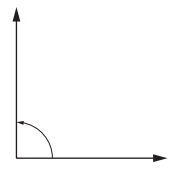
Type of angle: ___
Angle measure: ___
Answer:

Type of angle: Right Angle
Angle measure: 90  °
Explanation :
An angle of 90°, as in a corner of a square, or formed by dividing a circle into quarters.

Question 2.

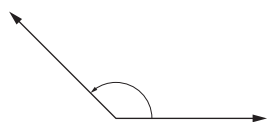
Type of angle: ___
Angle measure: ___
Answer:

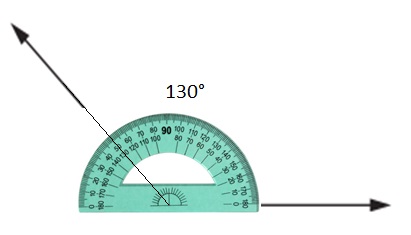
Type of angle: Obtuse Angle
Angle measure:
Explanation : 130°
An obtuse angle is a type of angle that is always larger than 90° but less than 180°. In other words, it lies between 90° and 180°

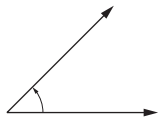
Question 3.

Type of angle: ___
Angle measure: ___
Answer:

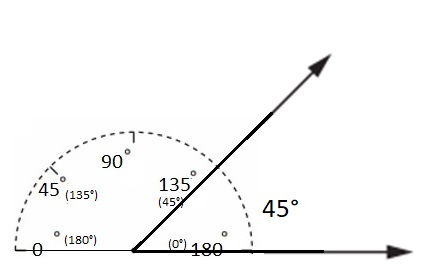
Type of angle: Acute Angle
Angle measure: 45°
Explanation :
An acute angle is an angle that measures less than 90 degrees .

Question 4.

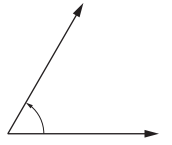
Type of angle: ___
Angle measure: ___
Answer:

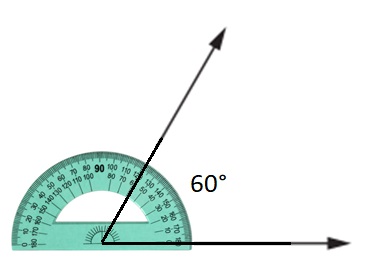
Type of angle: Acute Angle
Angle measure: 60°
Explanation :
An acute angle is an angle that measures less than 90 degrees .

Practice
Multiply.

Question 5.

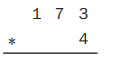
Answer:
173 × 4 = 692 .
Explanation :

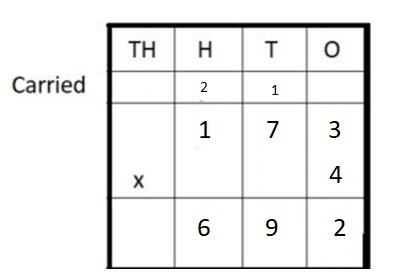
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 4.
3 × 4 = 12 = 1 ten + 2 ones
Write 2 in the ones column and carry 1 ten to tens place.
Step III: Multiply the digit at the tens place by 4.
7 × 4 = 28 tens
28 + 1 (carried) = 29 tens = 2 hundreds + 9 ten
Write 9 in ten place and carry 2 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 4.
1 hundred × 4 = 4 hundreds
4 hundreds + 2 hundreds (carried) = 6 hundreds
Write 6 in hundreds place

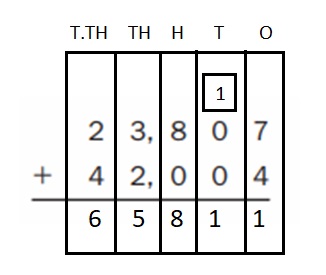
Question 6.

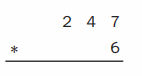
Answer:
247 × 6 = 1,482
Explanation :

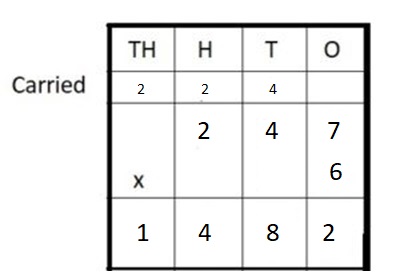
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 6.
7 × 6 = 42 = 4 ten + 2 ones
Write 2 in the ones column and carry 4 ten to tens place.
Step III: Multiply the digit at the tens place by 6.
4 × 6 = 24 tens
24 + 4 (carried) = 28 tens = 2 hundreds + 8 ten
Write 8 in ten place and carry 2 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 6.
2 hundred × 6 = 12 hundreds
12 hundreds + 2 hundreds (carried) = 1 thousands + 4 hundreds
Write 4 in hundreds place and carry 1 thousands to thousands place.

Question 7.

Answer:
34 × 20 = 680
Explanation :

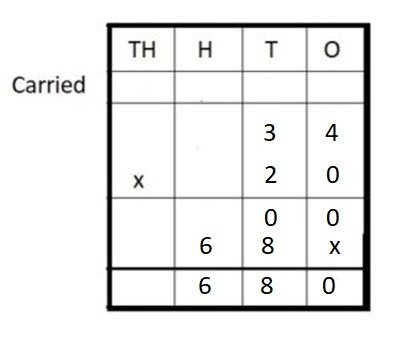
Step I: Arrange the numbers vertically.
Step II: Multiply 34 by 0 ones
34 × 0 = 00
Step III: Multiply 34 by 2 tens
34 × 20 = 680
Step IV: Add
00 + 680 = 680

Everyday Math Grade 4 Home Link 6.10 Answer Key

Measuring Angles with a Protractor

First estimate whether the angles measure more or less than 90°. Then use a half-circle protractor to measure them.

Question 1.

Answer:

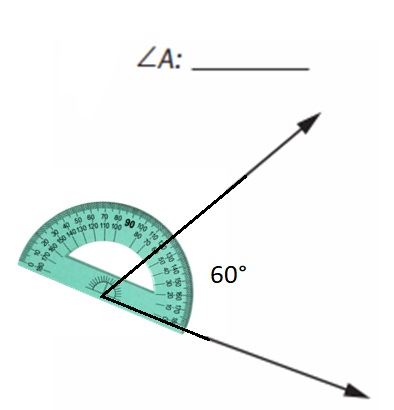
Question 2.

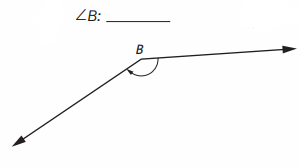
Answer:

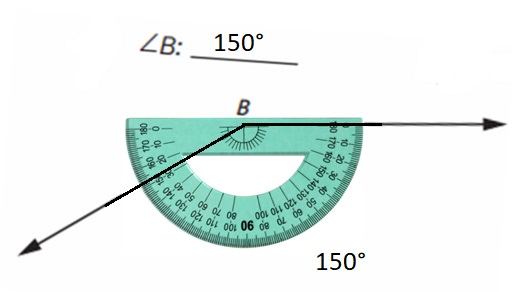
Question 3.

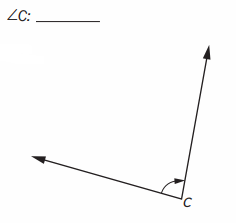
Answer:

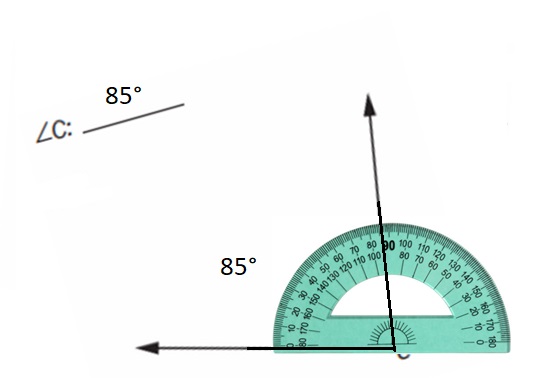
Question 4.
∠QRS: ___
Answer:

Explanation:
∠QRS is drawn at 30 ° using Protractor .

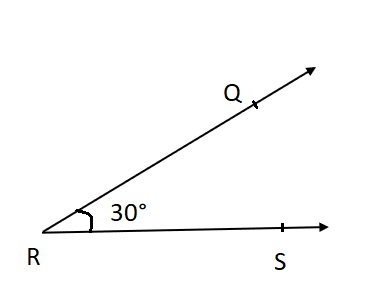
Question 5.
∠NOP: ___
Answer:

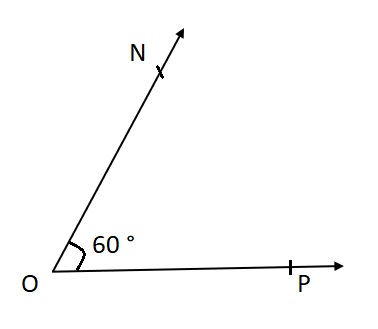
Explanation:
∠NOP is drawn at 60 ° using Protractor .

Question 6.
∠KLM: ___
Answer:

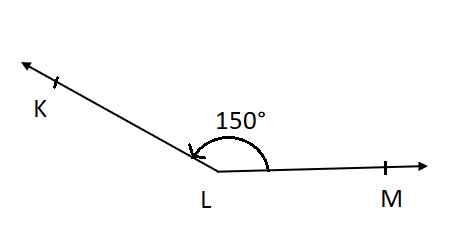
Explanation:
∠NOP is drawn at 150 ° using Protractor .

Practice

Question 7.

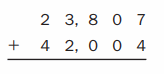
Answer:

Question 8.

Answer:

Question 9.

Answer:

Question 10.

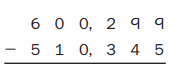
Answer:

Everyday Math Grade 4 Home Link 6.11 Answer Key

Finding Angle Measures

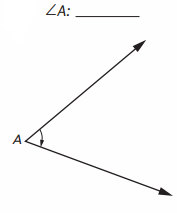
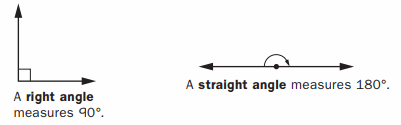
Find the unknown angle measures in Problems 1–6. Do not use a protractor.

Question 1.

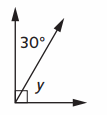
Equation with unknown: ___
Answer: ___
Angle formed in above image is right angle
Right Angle = 90  °
30  ° + y = 90  °
y = 90 ° – 30  °
y = 60  ° .

Question 2.

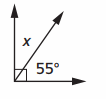
Equation with unknown: ___
Answer: ___
Angle formed in above image is right angle
Right Angle = 90  °
55 ° + x = 90  °
x = 90 ° – 55 °
x = 35 ° .

Question 3.

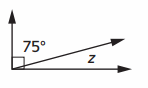
Equation with unknown: ___
Answer: ___
Angle formed in above image is right angle
Right Angle = 90  °
75 ° + z = 90  °
z = 90 ° – 75 °
z = 15 ° .

Question 4.

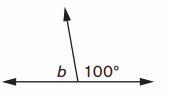
Equation with unknown: ___
Answer: ___
Angle formed in above image is straight angle
Straight Angle = 180  °
100 ° + b = 180  °
b = 180 ° –  100 °
b = 80° .

Question 5.

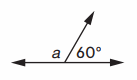
Equation with unknown: ___
Answer: ___
Angle formed in above image is straight angle
Straight Angle = 180  °
60 ° + a = 180  °
a = 180 ° –  60 °
a = 120° .

Question 6.

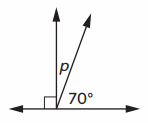
Equation with unknown: ___
Answer: ___
Angle formed in above image is right angle on a straight angle
Straight Angle = 180 °
Right angle = 90°
90 ° + p + 70° = 180  °
p + 160° = 180  °
p = 180 ° –  160 °
p = 20° .

Practice

Order the fractions from smallest to largest.

Question 7.
\(\frac{7}{10}\), \(\frac{7}{8}\), \(\frac{7}{12}\), \(\frac{7}{9}\) ___
Answer:
\(\frac{7}{10}\), \(\frac{7}{8}\), \(\frac{7}{12}\), \(\frac{7}{9}\)
lcm of 10,8, 12, and 9 = 360
\(\frac{252}{360}\), \(\frac{315}{360}\), \(\frac{210}{360}\), \(\frac{280}{360}\)
\(\frac{7}{12}\) < \(\frac{7}{10}\) < \(\frac{7}{9}\) < \(\frac{7}{8}\)
Explanation :
Fractions with the same numerators means that we’re talking about the same number of parts. So to compare fractions with the same numerator, all you have to do is compare the denominators. The fraction with the bigger denominator is smaller. or You cannot compare the fractions directly because they have different denominators. You need to find a common denominator for the given fractions and then compare the numerator values . greater the numerator greater the fraction .

Question 8.
\(\frac{5}{9}\), \(\frac{99}{100}\), \(\frac{1}{4}\), \(\frac{9}{10}\) ___
Answer:
\(\frac{5}{9}\), \(\frac{99}{100}\), \(\frac{1}{4}\), \(\frac{9}{10}\)
lcm of 9, 100, 4 and 10 = 900
\(\frac{500}{900}\), \(\frac{891}{900}\), \(\frac{225}{900}\), \(\frac{810}{10}\)
\(\frac{225}{900}\) < \(\frac{500}{900}\) < \(\frac{810}{10}\) < \(\frac{891}{900}\)
\(\frac{1}{4}\) < \(\frac{5}{9}\) < \(\frac{9}{10}\) < \(\frac{99}{100}\)
Explanation :
You cannot compare the fractions directly because they have different denominators. You need to find a common denominator for the given fractions and then compare the numerator values . greater the numerator greater the fraction .

Everyday Math Grade 4 Home Link 6.12 Answer Key

Solving Number Stories

Write a number model with an unknown to represent each problem. Then solve.

Question 1.
Martin had some leftover fruit from making fruit salad. He had \(\frac{3}{12}\) pound of strawberries and \(\frac{1}{12}\) pound of blueberries.
Which fruit weighed more? ___
Answer :
Quantity of Strawberries = \(\frac{3}{12}\) pound .
Quantity of blueberries = \(\frac{1}{12}\) pound .
\(\frac{3}{12}\) > \(\frac{1}{12}\)
that means strawberries weight more .
Explanation :
The Fractions whose denominator are same then compare the numerator, greater the numerator greater the fraction .

a. How many pounds of fruit did Martin have left?
Number model with unknown: ____
Answer: ___ pound
Answer:
Quantity of Strawberries = \(\frac{3}{12}\) pound .
Quantity of blueberries = \(\frac{1}{12}\) pound .
Total pounds of fruits = \(\frac{3}{12}\) + \(\frac{1}{12}\) = \(\frac{4}{12}\) = \(\frac{1}{3}\) pounds .

b. How much more did the strawberries weigh than the blueberries?
Number model with unknown: ____
Answer: ___ pound
Answer:
Quantity of Strawberries = \(\frac{3}{12}\) pound .
Quantity of blueberries = \(\frac{1}{12}\) pound .
\(\frac{3}{12}\) > \(\frac{1}{12}\)
Quantity of strawberries more than blueberries = \(\frac{3}{12}\) – \(\frac{1}{12}\) = \(\frac{2}{12}\) = \(\frac{1}{6}\) pounds .

Question 2.
Charlotte and Beth each made a vegetable salad to take to a reunion. Together the salads weighed 6 pounds. Charlotte’s salad weighed 3\(\frac{1}{2}\) pounds.
a. How much did Beth’s salad weigh?
Number model with unknown: ____
Answer: ___ pounds
Total Weight of salads = 6 pounds  .
Weight of Charlotte’s salad = 3\(\frac{1}{2}\) = \(\frac{7}{2}\) pounds.
Weight of Beth’s Salad = 6 – \(\frac{7}{2}\) = \(\frac{12}{2}\) – \(\frac{7}{2}\)  = \(\frac{5}{2}\) =2\(\frac{1}{2}\) pounds .

b. How much more did Charlotte’s salad weigh than Beth’s?
Number model with unknown: ____
Answer: ___ pound
Weight of Charlotte’s salad = 3\(\frac{1}{2}\) = \(\frac{7}{2}\) pounds.
Weight of Beth’s Salad = 2\(\frac{1}{2}\) = \(\frac{5}{2}\) pounds .
Weight of Charlotte’s salad more than Beth’s salad = \(\frac{7}{2}\) – \(\frac{5}{2}\) = \(\frac{2}{2}\) = 1 pound .

Question 3.
Andy’s potato salad weighed 1\(\frac{3}{8}\) pounds more than Mardi’s. Mardi’s potato salad
weighed 4\(\frac{2}{8}\) pounds. How much did Andy’s potato salad weigh?
Number model with unknown: ___
Answer: __ pounds
Weight of Mardi’s potato salad = 4\(\frac{2}{8}\) = \(\frac{34}{8}\) pounds.
Weight of Andy potato salad = 1\(\frac{3}{8}\) + 4\(\frac{2}{8}\) = \(\frac{11}{8}\) + \(\frac{34}{8}\) = \(\frac{45}{8}\) pounds .
Therefore, Weight of Andy potato salad = \(\frac{45}{8}\) = 5\(\frac{5}{8}\)  pounds .

Practice

Question 4.
826 ∗ 5 = ___
Answer:
826 ∗ 5 = 4,130
Explanation :

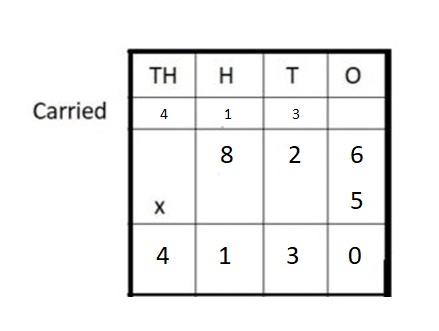
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 5.
6 × 5 = 30 = 3 ten + 0 ones
Write 0 in the ones column and carry 3 ten to tens place.
Step III: Multiply the digit at the tens place by 5.
2 × 5 = 10 tens
10 + 3 (carried) = 13 tens = 1 hundreds + 3 ten
Write 3 in ten place and carry 1 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 5.
8 hundred × 5 = 40 hundreds
40 hundreds + 4 hundreds (carried) = 4 thousands + 4 hundreds
Write 4 in hundreds place and carry 4 thousands to thousands place.

Question 5.
48 ∗ 50 = ___
Answer:
48 ∗ 50 = 2440
Explanation :

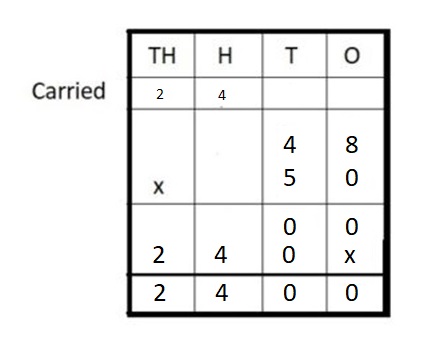
Step I: Arrange the numbers vertically.
Step II: Multiply 48 by 0 ones
48 × 0 = 00
Step III: Multiply 48 by 5 tens
48 × 50 = 2400
Step IV: Add
00 + 2400 = 2400

Everyday Math Grade 4 Home Link 6.13 Answer Key

Multiplying a Fraction by a Whole Number

Solve. Use drawings, words, and equations to represent the problems.

Question 1.
5 vans were needed for a camp field trip. There were 9 children per van.
How many children went on the field trip? __ children
Drawing:
Words: __ groups of __
Addition equation: ___
Multiplication equation: ___
Answer :

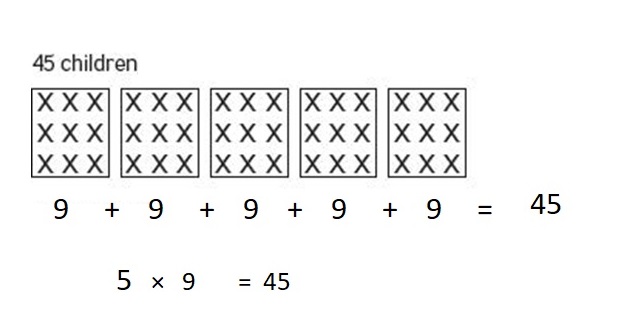
Explanation :
Number of Vans = 5
Number of children per van = 9
Number of children went for trip = Number of vans × Number of children per van = 5 × 9 = 45 children’s .
or
Number of children went for trip = adding number of children per van that is 9 for 5 times as there are 5 vans = 9 + 9 + 9 + 9 + 9  = 45 children’s .

Question 2.
Penny and her 2 friends each ate \(\frac{1}{6}\) of a cake. How much cake did they eat? __ of a cake
Drawing:
Words: __ groups of ___
Addition equation: ___
Multiplication equation: __
Answer:

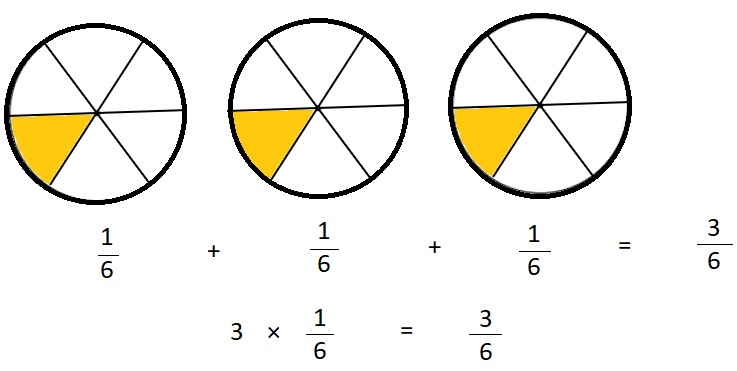
Number of people = 3
Fraction of cake ate by each person = \(\frac{1}{6}\)
Total Fraction of cake ate by them = adding \(\frac{1}{6}\) for 3 times . = \(\frac{1}{6}\)  + \(\frac{1}{6}\)  + \(\frac{1}{6}\)  = \(\frac{3}{6}\) = \(\frac{1}{2}\) of a cake
or
Total Fraction of cake ate by them = Number of people × Fraction of cake ate by each person = 3 × \(\frac{1}{6}\) = 1 × \(\frac{1}{2}\) =  \(\frac{1}{2}\) of a cake .

Question 3.
Christopher wants to give his 4 friends \(\frac{3}{5}\) of a veggie pizza each.
How much veggie pizza will he need? __ veggie pizzas
Drawing:
Words: __ groups of __
Addition equation: ___
Multiplication equation: ___
Answer :

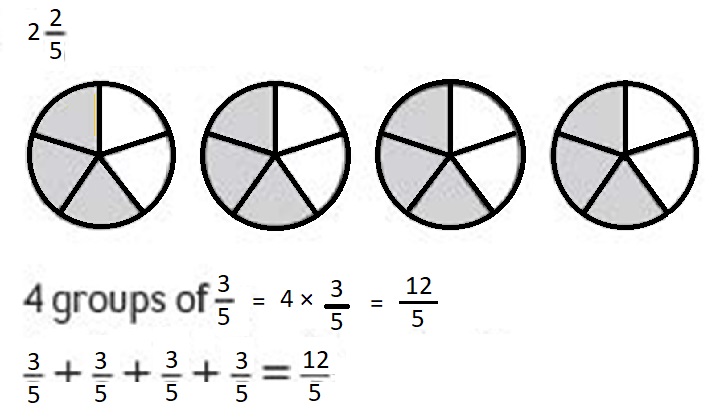
Number of friends = 4
Fraction of pizza each friend get = \(\frac{3}{5}\) each
Total fraction of pizza 4 friends get = \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\)+ \(\frac{3}{5}\) = \(\frac{12}{5}\) = 2\(\frac{2}{5}\) .
or
Total fraction of pizza 4 friends get = Number of friends  × Fraction of pizza each friend get  = 4 × \(\frac{3}{5}\) = \(\frac{12}{5}\) = 2 \(\frac{2}{5}\) .

Practice

Question 4.
84 / 6 = ___
Answer:
84 / 6 = 24
Explanation :

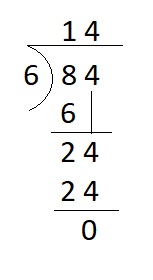
Question 5.
76 ÷ 4 = __
Answer:
76 ÷ 4 = 19
Explanation :

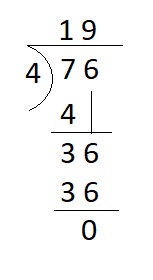
Question 6.
__ = 90 ÷ 5
Answer:
18 = 90 ÷ 5
Explanation :