Everyday Mathematics 4th Grade Answer Key Unit 5 Fraction and Mixed-Number Computation; Measurement
Everyday Math Grade 4 Home Link 5.1 Answer Key
Decomposing Fractions
Family Note In class today your child learned to decompose fractions into smaller parts.
For example, \(\frac{5}{6}\) can be decomposed into \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) , \(\frac{2}{6}\) + \(\frac{3}{6}\), \(\frac{1}{6}\) + \(\frac{4}{6}\), and so on.
Question 1.

Answer:
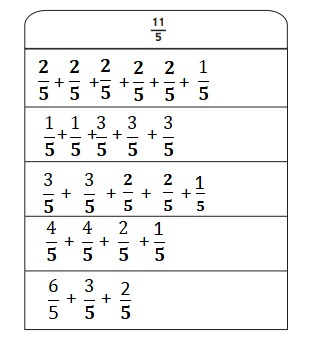
Explanation :
\(\frac{11}{5}\) is decomposed into different smaller fractions and combined as shown in the above figure .
Question 2.

Answer :
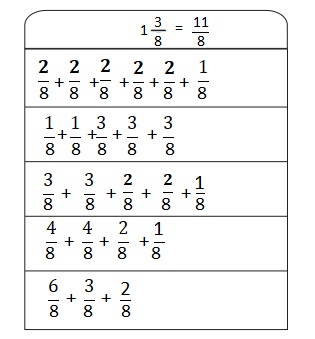
Explanation :
\(\frac{11}{8}\) is decomposed into different smaller fractions and combined as shown in the above figure .
3. Decompose \(\frac{8}{12}\) in more than one way into a sum of fractions with the same denominator.
Record each decomposition with an equation and justify it by shading the circle.
a. Equation: ___
Answer :
Equation : \(\frac{4}{12}\) + \(\frac{4}{12}\) = \(\frac{8}{12}\)
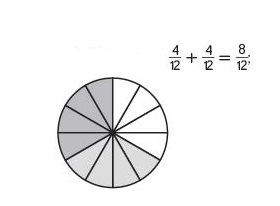
Explanation :
Given Circle is divided into 12 parts . Each part is a fraction of \(\frac{1}{12}\) so, to form \(\frac{8}{12}\) it is decomposed into \(\frac{4}{12}\) + \(\frac{4}{12}\) where, 2 – 4 parts are coloured in different colors as shown in above figure .
b. Equation: ___
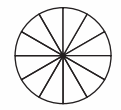
Answer :
Equation : \(\frac{2}{12}\) + \(\frac{2}{12}\) + \(\frac{2}{12}\) + \(\frac{2}{12}\) = \(\frac{8}{12}\)
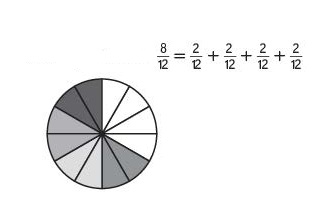
Explanation :
Given Circle is divided into 12 parts . Each part is a fraction of \(\frac{1}{12}\) so, to form \(\frac{8}{12}\) it is decomposed into \(\frac{2}{12}\) + \(\frac{2}{12}\) + \(\frac{2}{12}\) + \(\frac{2}{12}\) where, 4 – 2 parts are coloured in different colors as shown in above figure .
Practice
Question 4.
9 ∗ 785 = ___
Answer:
9 ∗ 785 = 7065
Explanation :
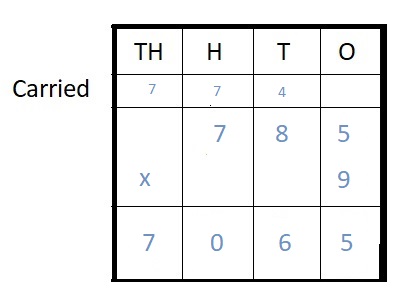
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 9.
5 × 9 = 45 = 4 ten + 5 ones
Write 5 in the ones column and carry 4 ten to tens place.
Step III: Multiply the digit at the tens place by 9.
8 × 9 = 72 tens
72 + 4 (carried) = 76 tens = 7 hundreds + 6 ten
Write 6 in ten place and carry 7 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 9
7 hundred × 9 = 63 hundreds
63 hundreds + 7 hundreds (carried) = 80 hundreds =8 thousands + 0 hundreds
Write 0 in hundreds place and carry 8 thousands to the thousands place .
Question 5.
461 ∗ 7 = ___
Answer:
461 ∗ 7 = 3227
Explanation :
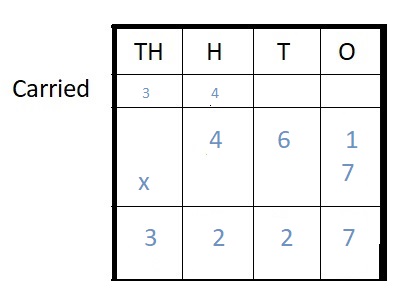
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 7.
1 × 7 = 7
Write 7 in the ones column .
Step III: Multiply the digit at the tens place by 7.
6 × 7 = 42 tens
42 tens = 4 hundreds + 2 ten
Write 2 in ten place and carry 4 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 7
4 hundred × 7 = 28 hundreds
28 hundreds + 4 hundreds (carried) = 32 hundreds = 3 thousands + 2 hundreds
Write 2 in hundreds place and carry 3 thousands to the thousands place .
Question 6.
644 ∗ 4 = ___
Answer:
644 ∗ 4 = 2576
Explanation :
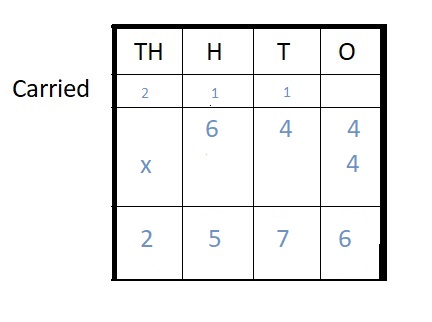
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 4.
4 × 4 = 16 = 1 ten + 6 ones
Write 6 in the ones column and carry 1 ten to tens place.
Step III: Multiply the digit at the tens place by 4.
4 × 4 = 16 tens
16 + 1 (carried) = 17 tens = 1 hundreds + 7 ten
Write 7 in ten place and carry 1 hundreds to hundreds place.
Step IV: Multiply the digit at hundreds place by 4
6 hundred × 4 = 24 hundreds
24 hundreds + 1 hundreds (carried) = 25 hundreds =2 thousands + 5 hundreds
Write 5 in hundreds place and carry 2 thousands to the thousands place .
Question 7.
___ = 39 ∗ 50
Answer:
1950 = 39 ∗ 50
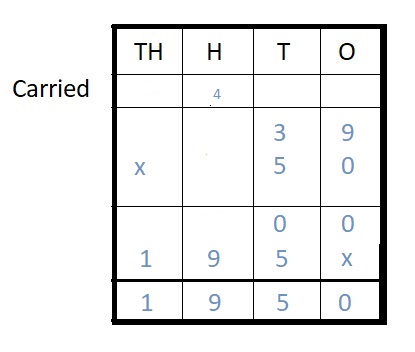
Explanation :
Step I: Arrange the numbers vertically.
Step II: Multiply 39 by 0 ones
39 × 0 = 00
Step III: Multiply 39 by 5 tens
39 × 50 = 1950
Step IV: Add
00 + 1950 = 1950
Everyday Math Grade 4 Home Link 5.2 Answer Key
What Is the Whole?
For Problems 1-3, use your Geometry Template or sketch the shapes.
Question 1.
Suppose is  is \(\frac{1}{4}\). Draw each of the following:
is \(\frac{1}{4}\). Draw each of the following:
Answer :
Explanation :
Each  is \(\frac{1}{4}\) so,
is \(\frac{1}{4}\) so,
To represent 1, 4  are drawn .
are drawn .
To represent 1 \(\frac{1}{2}\), 6  are drawn .
are drawn .
To represent 2, 8  are drawn .
are drawn .
Question 2.
Suppose 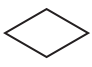 is \(\frac{2}{3}\). Draw each of the following:
is \(\frac{2}{3}\). Draw each of the following:
a. \(\frac{1}{3}\)
b. 1
c. \(\frac{4}{3}\)
d. 2
Answer:
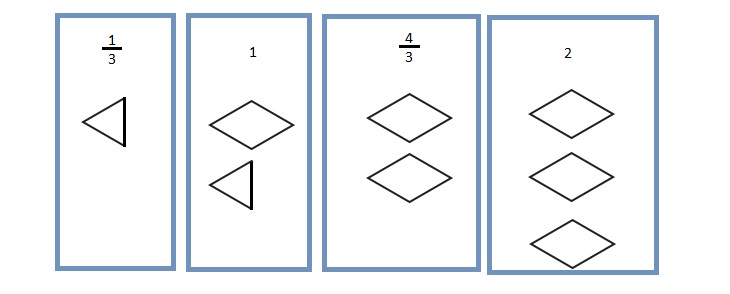
Suppose  is \(\frac{2}{3}\) then half of
is \(\frac{2}{3}\) then half of  is \(\frac{1}{3}\) .
is \(\frac{1}{3}\) .
Explanation :
Each  is \(\frac{2}{3}\) so,
is \(\frac{2}{3}\) so,
a. To represent \(\frac{1}{3}\), half of  is drawn .
is drawn .
b. To represent 1, 1 and half  are drawn .
are drawn .
c. To represent \(\frac{4}{3}\), 2  are drawn .
are drawn .
d. To represent 2, 3  are drawn .
are drawn .
Question 3.
Suppose 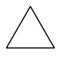 is \(\frac{1}{3}\). Draw each of the following:
is \(\frac{1}{3}\). Draw each of the following:
a. \(\frac{3}{3}\)
b. 2
c. \(\frac{5}{3}\)
d. 1\(\frac{1}{3}\)
Answer:
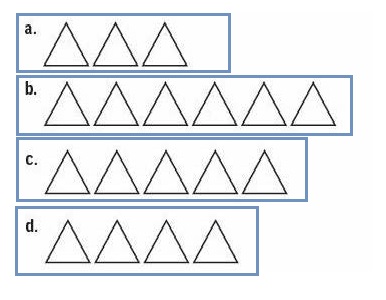
Explanation :
Each  is \(\frac{1}{3}\) so,
is \(\frac{1}{3}\) so,
a. To represent \(\frac{3}{3}\), 3  are drawn .
are drawn .
b. To represent 2, 6  are drawn .
are drawn .
c. To represent \(\frac{5}{3}\), 5  are drawn .
are drawn .
d. To represent 1 \(\frac{1}{3}\) , 4  are drawn .
are drawn .
Practice
Question 4.
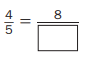
Answer:
\(\frac{4}{5}\) = \(\frac{8}{10}\).
Explanation :
\(\frac{4}{5}\) = \(\frac{4 × 2}{5 × 2}\) = \(\frac{8}{10}\)
Multiply numerator and denominator by 2 .
Question 5.
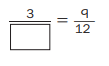
Answer:
\(\frac{3}{4}\) = \(\frac{9}{12}\).
Explanation :
\(\frac{9}{12}\) = \(\frac{9 ÷ 3}{12 ÷ 3}\) = \(\frac{3}{4}\)
Divide numerator and denominator by 3 .
Question 6.
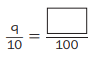
Answer:
\(\frac{9}{10}\) = \(\frac{90}{100}\).
Explanation :
\(\frac{9}{10}\) = \(\frac{9 × 10}{10 × 10}\) = \(\frac{90}{100}\)
Multiply numerator and denominator by 10 .
Everyday Math Grade 4 Home Link 5.3 Answer Key
Adding Fractions
Solve the number stories. Use a different strategy for each one.
Question 1.
The park department wants to have new trees planted. They agreed that \(\frac{1}{10}\) of the trees will be oak, \(\frac{3}{10}\) will be pine, and \(\frac{2}{10}\) will be willow. They are undecided about the rest. What fraction of the trees will be oak, willow, or pine?
a. Fill in the whole box.

Answer:

b. Number model with unknown:
Answer:
Number of oak trees = \(\frac{1}{10}\)
Number of oak trees = \(\frac{3}{10}\)
Number of oak trees = \(\frac{2}{10}\)
Total Trees = \(\frac{1}{10}\) + \(\frac{3}{10}\) + \(\frac{2}{10}\) = \(\frac{6}{10}\)
c. One way to solve a fraction addition problem:
Answer:
fraction is represented as \(\frac{6}{10}\) that means total is 10
d. Answer (with unit): ______
Answer:
Number of oak trees = \(\frac{1}{10}\)
Number of oak trees = \(\frac{3}{10}\)
Number of oak trees = \(\frac{2}{10}\)
Total Trees = \(\frac{1}{10}\) + \(\frac{3}{10}\) + \(\frac{2}{10}\) = \(\frac{6}{10}\) oak, willow, or pine trees .
Question 2.
The Patels have a DVD collection. Three-eighths of the DVDs are animated. Two-eighths of them are mysteries. One-eighth are comedies. The rest are about travel. What fraction of the DVDs are not about travel?
a. Fill in the whole box.

Answer:

b. Number model with unknown:
Answer:
Total Fraction = \(\frac{8}{8}\)
Fraction of DVDs are animated = \(\frac{3}{8}\)
Fraction of DVDs are mysteries = \(\frac{2}{8}\)
Fraction of DVDs are comedies = \(\frac{1}{8}\)
Fraction of DVDs that are not about travel = \(\frac{3}{8}\) + \(\frac{2}{8}\) – \(\frac{1}{8}\) = \(\frac{8}{8}\) – \(\frac{6}{8}\) = \(\frac{2}{8}\) = \(\frac{1}{4}\) DVD’S .
c. A different way to solve a fraction addition problem:
Answer:
Explanation :
The Denominator of the Fraction represent the total as Eight .
d. Answer (with unit):
Answer:
Total Fraction = \(\frac{8}{8}\)
Fraction of DVDs are animated = \(\frac{3}{8}\)
Fraction of DVDs are mysteries = \(\frac{2}{8}\)
Fraction of DVDs are comedies = \(\frac{1}{8}\)
Fraction of DVDs that are not about travel = \(\frac{3}{8}\) + \(\frac{2}{8}\) + \(\frac{1}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\) DVD’SAdd.
Question 3.
\(\frac{2}{5}\) + \(\frac{1}{5}\) = ___
Answer:
\(\frac{2}{5}\) + \(\frac{1}{5}\) = \(\frac{3}{5}\)
Question 4.
\(\frac{1}{2}\) + \(\frac{3}{2}\) = ___
Answer:
\(\frac{1}{2}\) + \(\frac{3}{2}\) = \(\frac{4}{2}\) = 2
Question 5.
\(\frac{5}{6}\) + \(\frac{5}{6}\) = ___
Answer:
\(\frac{5}{6}\) + \(\frac{5}{6}\) = \(\frac{10}{6}\) = \(\frac{5}{3}\) = 1\(\frac{2}{3}\)
Question 6.
\(\frac{1}{3}\) + \(\frac{2}{3}\) + \(\frac{1}{3}\) = ___
Answer:
\(\frac{1}{3}\) + \(\frac{2}{3}\) + \(\frac{1}{3}\) = \(\frac{4}{3}\) = 1\(\frac{1}{3}\)
Practice
Represent the fractions as decimals.
Question 7.
\(\frac{4}{10}\) = ___
Answer:
\(\frac{4}{10}\) = 0.4
Explanation :
Since the denominator 10 has a single zero, we shift the decimal point in 4.0 one place to the left and get . 4 or 0.4 as the answer
Question 8.
\(\frac{40}{100}\) = ___
Answer:
\(\frac{40}{100}\) = 0.04
Explanation :
Since the denominator 100 has two zero’s, we shift the decimal point in 40.0 two place to the left and get . 04 or 0.04 as the answer
Question 9.
\(\frac{6}{10}\) = __
Answer:
\(\frac{6}{10}\) = 0.6
Explanation :
Since the denominator 10 has a single zero, we shift the decimal point in 6.0 one place to the left and get .6 or 0.6 as the answer
Question 10.
\(\frac{6}{100}\) = ___
\(\frac{60}{100}\) = 0.06
Explanation :
Since the denominator 100 has two zero’s, we shift the decimal point in 60.0 two place to the left and get . 06 or 0.06 as the answer
Everyday Math Grade 4 Home Link 5.4 Answer Key
Mixed-Number Addition
Solve the number stories. Use a different strategy for each one.
Question 1.
The art class had a box filled with balls of yarn. The students used 6\(\frac{2}{3}\) balls for a project. There are now 2\(\frac{2}{3}\) balls left in the box. How many balls of yarn did the art class start with?
a. Fill in the whole box.

Answer:

b. Number model with unknown:
Answer:
Number of yarn balls used for project = 6\(\frac{2}{3}\) = \(\frac{20}{3}\) .
Number of yarn balls left = 2\(\frac{2}{3}\) = \(\frac{8}{3}\) .
Total Number of yarn balls = \(\frac{20}{3}\) + \(\frac{8}{3}\) = \(\frac{28}{3}\) = 9\(\frac{1}{3}\) .
c. One way to solve a mixed-number addition problem:
Answer:
I decomposed the mixed numbers so, First combine the wholes and then fractions
6\(\frac{2}{3}\) + 2\(\frac{2}{3}\) = 6 + \(\frac{2}{3}\) + 2 + \(\frac{2}{3}\) = 8 + \(\frac{4}{3}\) = 9 + \(\frac{1}{3}\) = 9\(\frac{1}{3}\) .
d. Answer (with unit): ______
Answer:
Number of yarn balls used for project = 6\(\frac{2}{3}\) = \(\frac{20}{3}\) .
Number of yarn balls left = 2\(\frac{2}{3}\) = \(\frac{8}{3}\) .
Total Number of yarn balls = \(\frac{20}{3}\) + \(\frac{8}{3}\) = \(\frac{28}{3}\) = 9\(\frac{1}{3}\) .
Therefore, Total Number of yarn balls = 9\(\frac{1}{3}\) balls .
Question 2.
Mrs. Meyers is growing vines along the sides of her house. On the west side the vines are 2\(\frac{4}{10}\) meters tall. On the east side the vines are 5\(\frac{8}{10}\) meters taller than the ones on the west side. How tall are the vines on the east side?
a. Fill in the whole box.

Answer:

b. Number model with unknown:
Answer:
Fraction of growing vines taller on west side = 2\(\frac{4}{10}\) tall
Fraction of growing vines taller on east side = 5\(\frac{8}{10}\) meters taller than the ones on the west side. = 5\(\frac{8}{10}\) + 2\(\frac{4}{10}\) = 5 + \(\frac{8}{10}\) + 2 + \(\frac{4}{10}\) = 7 + \(\frac{12}{10}\) = 8 + \(\frac{2}{10}\) = 8\(\frac{2}{10}\) = 8\(\frac{1}{5}\) meters .
Therefore, Fraction of growing vines taller on east side = 8\(\frac{2}{10}\) = 8\(\frac{1}{5}\) meters .
c. A different way to solve a mixed-number addition problem:
Answer:
I decomposed the mixed numbers so, First combine the wholes and then fractions
5\(\frac{8}{10}\) + 2\(\frac{4}{10}\) = 5 + \(\frac{8}{10}\) + 2 + \(\frac{4}{10}\) = 7 + \(\frac{12}{10}\) = 8 + \(\frac{2}{10}\) = 8\(\frac{2}{10}\) = 8\(\frac{1}{5}\) meters .
d. Answer (with unit):
Answer:
Fraction of growing vines taller on west side = 2\(\frac{4}{10}\) tall
Fraction of growing vines taller on east side = 5\(\frac{8}{10}\) meters taller than the ones on the west side. = 5\(\frac{8}{10}\) + 2\(\frac{4}{10}\) = 5 + \(\frac{8}{10}\) + 2 + \(\frac{4}{10}\) = 7 + \(\frac{12}{10}\) = 8 + \(\frac{2}{10}\) = 8\(\frac{2}{10}\) = 8\(\frac{1}{5}\) meters .
Therefore, Fraction of growing vines taller on east side = 8\(\frac{2}{10}\) = 8\(\frac{1}{5}\) meters .
Add. Show your work.
Question 3.
5\(\frac{2}{6}\) + 3\(\frac{1}{6}\) = ___
Answer:
5\(\frac{2}{6}\) + 3\(\frac{1}{6}\) = \(\frac{32}{6}\) + \(\frac{19}{6}\) = \(\frac{51}{6}\) = \(\frac{17}{2}\) = 8 \(\frac{1}{2}\) .
Question 4.
1\(\frac{5}{8}\) + 2\(\frac{3}{8}\) = ___
Answer:
1\(\frac{5}{8}\) + 2\(\frac{3}{8}\) = \(\frac{13}{8}\) + \(\frac{19}{8}\) = \(\frac{32}{8}\) = 4 .
Question 5.
3\(\frac{3}{4}\) + 2\(\frac{3}{4}\) = ___
Answer:
3\(\frac{3}{4}\) + 2\(\frac{3}{4}\) = \(\frac{15}{4}\) + \(\frac{11}{4}\) = \(\frac{26}{4}\) = \(\frac{13}{2}\) = 6\(\frac{1}{2}\) .
Question 6.
3\(\frac{2}{5}\) + 1\(\frac{4}{5}\) + 2\(\frac{3}{5}\) = ___
Answer:
3\(\frac{2}{5}\) + 1\(\frac{4}{5}\) + 2\(\frac{3}{5}\) = \(\frac{17}{5}\) + \(\frac{9}{5}\) + \(\frac{13}{5}\) = \(\frac{39}{5}\) =7\(\frac{4}{5}\)
Practice
Question 7.
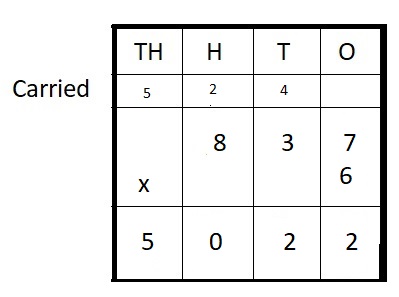
837 ∗ 6 = ___
Answer:
837 ∗ 6 = 5,022
Explanation :
Question 8.
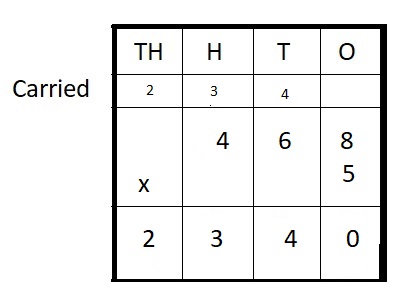
__ = 468 ∗ 5
Answer:
2,340 = = 468 ∗ 5
Explanation :
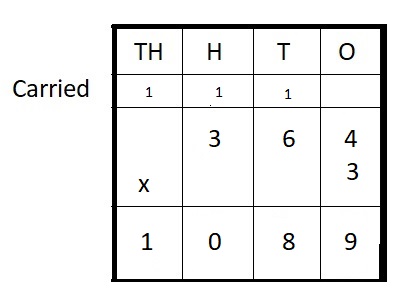
Question 9.
__ = 364 ∗ 3
Answer:
1,089 = = 364 ∗ 3
Explanation :
Question 10.
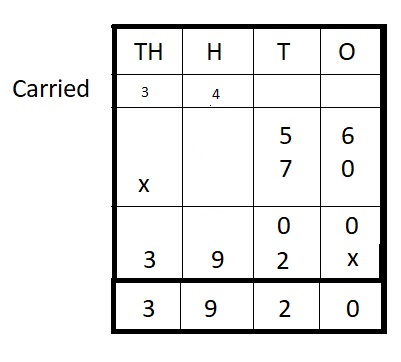
56 ∗ 70 = __
Answer:
56 ∗ 70 = 3,920
Explanation :
Everyday Math Grade 4 Home Link 5.5 Answer Key
Adding Tenths and Hundredths
Use what you know about equivalent fractions to add. Write an equation to show your work.
Question 1.
2 tenths + 15 hundredths
Equation (in words): _______
Answer:
Equation (in words):
2 tenths + 15 hundredths = 20 hundredths + 15 hundredths = 35 hundredths
Question 2.
\(\frac{68}{100}\) + \(\frac{3}{10}\)
Equation: ______
Answer:
Equation: \(\frac{68}{100}\) + \(\frac{3}{10}\) = \(\frac{68}{100}\) + \(\frac{30}{100}\) = \(\frac{98}{100}\) .
Question 3.
\(\frac{1}{10}\) + \(\frac{50}{100}\)
Equation: ______
Answer:
Equation: \(\frac{1}{10}\) + \(\frac{50}{100}\) = \(\frac{1}{10}\) + \(\frac{5}{10}\) = \(\frac{6}{10}\)
Question 4.
\(\frac{4}{10}\) + \(\frac{60}{100}\) + \(\frac{3}{10}\) + \(\frac{81}{100}\)
Equation: ______
Answer:
Equation: \(\frac{4}{10}\) + \(\frac{60}{100}\) + \(\frac{3}{10}\) + \(\frac{81}{100}\) = \(\frac{40}{100}\) + \(\frac{60}{100}\) + \(\frac{30}{100}\) + \(\frac{81}{100}\) = \(\frac{211}{100}\) = 2\(\frac{11}{100}\) .
Question 5.
1\(\frac{3}{10}\) + 5\(\frac{64}{100}\)
Equation: ____
Answer:
Equation: 1\(\frac{3}{10}\) + 5\(\frac{64}{100}\) = \(\frac{13}{10}\) + \(\frac{564}{100}\) = \(\frac{130}{100}\) + \(\frac{564}{100}\) = \(\frac{694}{100}\) = 6\(\frac{94}{100}\) .
Question 6.
3\(\frac{22}{100}\) + 2\(\frac{8}{10}\)
Equation: ______
Answer:
Equation: 3\(\frac{22}{100}\) + 2\(\frac{8}{10}\) = \(\frac{322}{100}\) + \(\frac{18}{10}\) = \(\frac{322}{100}\) + \(\frac{180}{100}\) = \(\frac{502}{100}\) = 5 \(\frac{2}{100}\)
Question 7.
\(\frac{15}{10}\) + \(\frac{78}{100}\)
Equation: ______
Answer:
Equation: \(\frac{15}{10}\) + \(\frac{78}{100}\) = \(\frac{150}{100}\) + \(\frac{78}{100}\) = \(\frac{228}{100}\) = 2\(\frac{28}{100}\)
Question 8.
Nicholas shaded \(\frac{40}{100}\) of his hundreds grid. Victor shaded \(\frac{5}{10}\) of his grid.
Who shaded more? ____
How much did they shade in all? ____ of a grid
Answer:
Fraction of grid shaded by Nicholas = \(\frac{40}{100}\) = \(\frac{4}{10}\) = 0.4
Fraction of grid shaded by Victor = \(\frac{5}{10}\) = 0.5
0.5 > 0.4 that means Victor shaded more than Nicholas .
Total fraction of grid shaded by both =\(\frac{4}{10}\) + \(\frac{5}{10}\) = \(\frac{9}{10}\) of a grid .
Practice +
Write three equivalent fractions.
Question 9.
\(\frac{1}{2}\) = ___
Answer:
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\)
Explanation :
Equivalent fractions are the fractions that have different numerator and denominator but are equal to the same value .
Question 10.
\(\frac{1}{3}\) = __
Answer:
\(\frac{1}{3}\) = \(\frac{2}{6}\) = \(\frac{3}{9}\) = \(\frac{4}{12}\)
Explanation :
Equivalent fractions are the fractions that have different numerator and denominator but are equal to the same value .
Question 11.
\(\frac{1}{4}\) = __
Answer:
\(\frac{1}{4}\) = \(\frac{2}{8}\) = \(\frac{3}{12}\) = \(\frac{4}{12}\)
Explanation :
Equivalent fractions are the fractions that have different numerator and denominator but are equal to the same value .
Question 12.
\(\frac{1}{5}\) =
Answer:
\(\frac{1}{5}\) = \(\frac{2}{10}\) = \(\frac{3}{15}\) = \(\frac{4}{20}\)
Explanation :
Equivalent fractions are the fractions that have different numerator and denominator but are equal to the same value .
Everyday Math Grade 4 Home Link 5.6 Answer Key
Fraction Error Finder
Consider this problem:
A king owns land outside of his castle.
He has partitioned the land to give as gifts to his 5 sons.
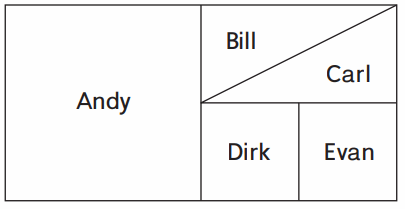
What fraction of the land did the king give to each of his sons?
Here is Zeke’s solution:
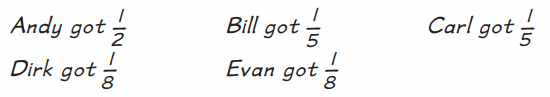
Question 1.
Identify Zeke’s two errors, correct them, and explain why your answer is correct.
Answer:
Bill and Carl also received \(\frac{1}{8}\) .
Explanation :
As per the above figure , Andy Got half of the whole = \(\frac{1}{2}\)
And other 4 sons received land from rest of the half .
Fraction of part Bill , Carl , Dirk and Evan received \(\frac{1}{4}\) part of \(\frac{1}{2}\) = \(\frac{1}{4}\) × \(\frac{1}{2}\) = \(\frac{1}{8}\) part .
Drik and Evan received in a Square area Where Bill and carl both land are in rectangle shape and diagonally intersected that means half of the rectangle area. so, all the land area is equally divided but in different shapes .
Question 2.
Write a fraction addition equation to represent the correct answers and show the sum of the pieces of land.
Answer:
Fraction of the Andy land = \(\frac{1}{2}\)
Fraction of the Bill land = \(\frac{1}{8}\)
Fraction of the Carl land = \(\frac{1}{8}\)
Fraction of the Drik land = \(\frac{1}{8}\)
Fraction of the Evan land = \(\frac{1}{8}\)
Total Land = \(\frac{1}{2}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) .
Practice
Use U.S. traditional addition and subtraction.
Question 3.
8,936 + 6,796 = ___
Answer:
8,936 + 6,796 = 15,732
Explanation :
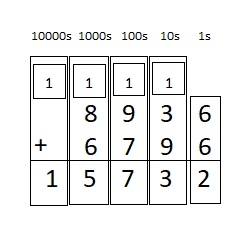
Step 1
Add the 1s: 6 + 6 = 12.
12 ones = 1 ten and 2 ones
Write 2 in the 1s place below the line.
Write 1 above the digits in the 10s place.
Step 2
Add the 10s: 3 + 9 + 1 = 13
13 tens = 1 hundred + 3 tens
Write 3 in the 10s place below the line.
Write 1 above the digits in the 100s place.
Step 3
Add the 100s: 9 + 7 + 1 = 17
17 hundreds = 1 thousand + 7 hundred
Write 7 in the 100s place below the line.
Write 1 above the digits in the 1000s place.
Step 4
Add the 1000s: 8 + 6 + 1 = 15
15 thousands= 1 ten thousand + 7 thousand
Write 7 in the 1000s place below the line.
Write 1 above the digits in the 10000s place.
No values to add in the ten thousand’s place so write 1 below the line in 10000s place .
Question 4.
635 – 392 = ___
Answer:
635 – 392 = 243
Explanation :
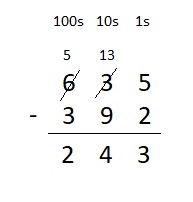
Step 1:
Start with the ones. Subtract the ones. 5 – 3 = 2 ones .
Step 2:
Go to the tens. Trade 1 hundred for 10 tens. Subtract the tens. 3 + 10 = 13 . 13 – 9 = 4 tens
Step 3:
Go to the hundreds. We don’t need to regroup, so just subtract 5 – 3 = 2 .
Question 5.
6,386 + 4,205 = ___
Answer:
6,386 + 4,205 = 10,591
Explanation :
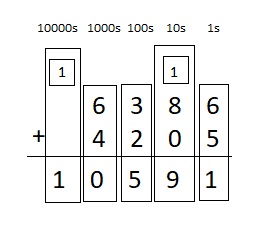
thousand
Step 1
Add the 1s: 6 + 5 = 11.
11 ones = 1 ten and 1 ones
Write 1 in the 1s place below the line.
Write 1 above the digits in the 10s place.
Step 2
Add the 10s: 8 + 0 + 1 = 9
Write 9 in the 10s place below the line.
Step 3
Add the 100s: 3 + 2 = 5
Write 5 in the 100s place below the line.
Step 4
Add the 1000s: 6 + 4 = 10.
10 thousands = 1 ten thousand and 1 thousand
Write 0 in the 1s place below the line.
Write 1 above the digits in the 10000s place.
No values to add in the ten thousand’s place so write 1 below the line in 10000s place .
Question 6.
900 – 463 =
Answer:
900 – 463 = 437
Explanation :
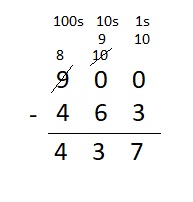
Step 1:
Start with the ones. Trade 1 ten for 10 ones. Subtract the ones. .
Step 2:
Go to the tens. Trade 1 hundred for 10 tens. Subtract the tens. 3 + 10 = 13 . 13 – 9 = 4 tens
Step 1:
Trade 1 from hundreds , we have
9 hundreds – 1 = 8 hundreds
0 tens + 10 tens = 10 tens .
Step 2 :
Trade 1 from tens , we have
10 tens – 1 = 9 tens
0 ones + 10 ones = 10 ones .
Step 3 :
Now subtract the values .we get differences as 437 .
Everyday Math Grade 4 Home Link 5.7 Answer Key
Subtracting Fractions
Solve the number stories. Use a different strategy for each one.
Question 1.
Elijah still had \(\frac{4}{5}\) of his allowance at the end of the month. Then he spent \(\frac{3}{5}\) of his original allowance on a movie ticket and popcorn. How much of Elijah’s allowance was left?
a. Fill in the whole box. 
b. Number model with unknown: _____
c . One way to solve a fraction subtraction problem:
d. Answer (with unit): ___
Answer:
a .

b.
Total Allowances = \(\frac{4}{5}\)
Allowances spent on Movie and pop corn = \(\frac{3}{5}\)
Allowances left = \(\frac{4}{5}\) – \(\frac{3}{5}\) = \(\frac{1}{5}\)
Therefore, allowances left = \(\frac{1}{5}\) of his allowances .
c.
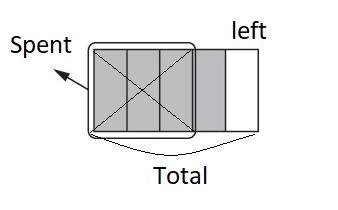
d.
Total Allowances = \(\frac{4}{5}\)
Allowances spent on Movie and pop corn = \(\frac{3}{5}\)
Allowances left = \(\frac{4}{5}\) – \(\frac{3}{5}\) = \(\frac{1}{5}\)
Therefore, allowances left = \(\frac{1}{5}\) of his allowances .
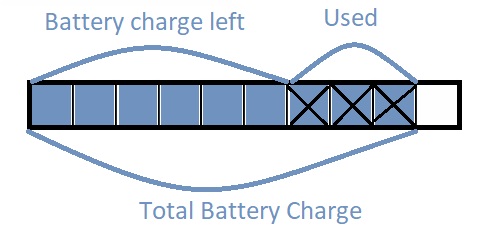
Question 2.
Kendra’s computer battery had \(\frac{9}{10}\) of a charge. After her sister Lydia borrowed the computer, the battery had \(\frac{3}{10}\) of a charge left. How much of the battery charge did Lydia use?
a. Fill in the whole box. 
b. Number model with unknown: ______
c. Another way to solve a fraction subtraction problem.
d. Answer (with unit): ______
Answer:
a.

b.
Total Battery charge = \(\frac{9}{10}\)
Charge left after lydia use = \(\frac{3}{10}\)
Charge used by lydia = \(\frac{9}{10}\) – \(\frac{3}{10}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\) charge .
c.
d.
Total Battery charge = \(\frac{9}{10}\)
Charge left after lydia use = \(\frac{3}{10}\)
Charge used by lydia = \(\frac{9}{10}\) – \(\frac{3}{10}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\) charge .
Therefore, Battery Charge used by lydia = \(\frac{6}{10}\) = \(\frac{3}{5}\) battery charge .
Subtract.
Question 3.
\(\frac{2}{2}\) – \(\frac{1}{2}\) = ___
Answer:
\(\frac{2}{2}\) – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Explanation :
\(\frac{2}{2}\) – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Question 4.
\(\frac{11}{6}\) – \(\frac{4}{6}\) = ___
Answer:
\(\frac{11}{6}\) – \(\frac{4}{6}\) = 1\(\frac{1}{6}\)
Explanation :
\(\frac{11}{6}\) – \(\frac{4}{6}\) = \(\frac{7}{6}\) = 1\(\frac{1}{6}\)
Question 5.
___ = 1 – \(\frac{1}{5}\)
Answer:
\(\frac{4}{5}\) = 1 – \(\frac{1}{5}\)
Explanation :
1 – \(\frac{1}{5}\) = \(\frac{5}{5}\) – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Practice
Question 6.
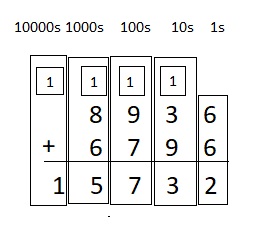
8,936 + 6,796 = ____
Answer:
8,936 + 6,796 = 15,732
Explanation :
Question 7.
____ = 4,635 – 2,392
Answer:
2,243 = 4,635 – 2,392
Explanation :

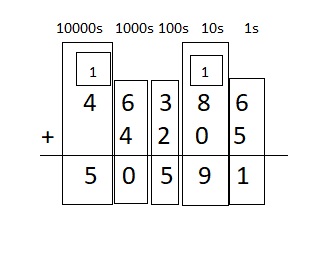
Question 8.
___ = 46,386 + 4,205
Answer:
50,591 = 46,386 + 4,205
Explanation :
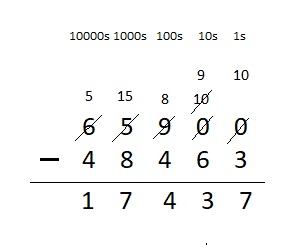
Question 9.
65,900 – 48,463 = ___
Answer:
65,900 – 48,463 = 17, 437 .
Explanation :
Everyday Math Grade 4 Home Link 5.8 Answer Key
Mixed-Number Subtraction
Solve the number stories. Use a different strategy for each one.
Question 1.
The chocolate chip cake recipe calls for 3\(\frac{1}{3}\) cups of milk. We only have 1\(\frac{2}{3}\) cups at home. How much more milk do we need?
a. Fill in the whole box.
b. Number model with unknown: ______
c. One way to solve a mixed-number subtraction problem:
d. Answer (with unit): ____
Answer:
a .
b.
Quantity of Milk Required for Chocolate cake = 3\(\frac{1}{3}\)
Quantity of milk at home = 1\(\frac{2}{3}\)
Quantity of Mor milk required = 3\(\frac{1}{3}\) – 1\(\frac{2}{3}\) = 3 + \(\frac{1}{3}\) – 1 – \(\frac{2}{3}\) = 1 + \(\frac{4}{3}\) – \(\frac{2}{3}\) = 1 + \(\frac{2}{3}\) = 1\(\frac{2}{3}\)
c.
First subtract the whole numbers and then subtract fractions .
\(\frac{1}{3}\) – 1\(\frac{2}{3}\) = 3 + \(\frac{1}{3}\) – 1 – \(\frac{2}{3}\) = 1 + \(\frac{4}{3}\) – \(\frac{2}{3}\) = 1 + \(\frac{2}{3}\) = 1\(\frac{2}{3}\)
d.
Quantity of milk required = = 1 + \(\frac{2}{3}\) = 1\(\frac{2}{3}\) cups of milk .
Question 2.
Lourdes is listening to an audio book that is 9 hours long. She has listened for 6\(\frac{1}{6}\) hours so far. How many hours of listening time are left?
a. Fill in the whole box.
b. Number model with unknown: ____
c. A different way to solve a mixed-number subtraction problem:
d. Answer (with unit): ______
Answer :
a.

b.
Time Required for listening to an audio book = 9 hours
Time spent in Reading = 6\(\frac{1}{6}\) hours = \(\frac{37}{6}\) hours
Time left in Reading = 9 – 6\(\frac{1}{6}\) = 9 – 6 – \(\frac{1}{6}\) = 3 – \(\frac{1}{6}\) = 2 – \(\frac{6}{6}\) – \(\frac{1}{6}\) = 2 – \(\frac{5}{6}\) = 2\(\frac{5}{6}\) .
Therefore, Time left in Reading = 2\(\frac{5}{6}\) hours .
c.
First subtract the whole numbers and then subtract fractions .
9 – 6\(\frac{1}{6}\) = 9 – 6 – \(\frac{1}{6}\) = 3 – \(\frac{1}{6}\) = 2 – \(\frac{6}{6}\) – \(\frac{1}{6}\) = 2 – \(\frac{5}{6}\) = 2\(\frac{5}{6}\) .
d.
Time left in Reading = 2\(\frac{5}{6}\) hours .
Subtract. Show your work.
Question 3.
4\(\frac{1}{2}\) – 3\(\frac{1}{2}\) =
Answer:
4\(\frac{1}{2}\) – 3\(\frac{1}{2}\) = 1
Explanation :
4\(\frac{1}{2}\) – 3\(\frac{1}{2}\) = \(\frac{9}{2}\) – \(\frac{7}{2}\) = \(\frac{2}{2}\) = 1
Question 4.
___ = 5\(\frac{8}{12}\) – 5\(\frac{3}{12}\)
Answer:
\(\frac{5}{12}\) = 5\(\frac{8}{12}\) – 5\(\frac{3}{12}\)
Explanation :
5\(\frac{8}{12}\) – 5\(\frac{3}{12}\) = \(\frac{68}{12}\) – \(\frac{63}{12}\) = \(\frac{5}{12}\)
Question 5.
4\(\frac{2}{5}\) – 1\(\frac{4}{5}\) = ___
Answer:
4\(\frac{2}{5}\) – 1\(\frac{4}{5}\) = 2\(\frac{3}{5}\)
Explanation :
4\(\frac{2}{5}\) – 1\(\frac{4}{5}\) = \(\frac{22}{5}\) – \(\frac{9}{5}\) = \(\frac{13}{5}\) = 2\(\frac{3}{5}\) .
Question 6.
__ = 9\(\frac{4}{10}\) – 3\(\frac{8}{10}\)
Answer:
5\(\frac{6}{10}\) = 9\(\frac{4}{10}\) – 3\(\frac{8}{10}\)
Explanation :
9\(\frac{4}{10}\) – 3\(\frac{8}{10}\) = \(\frac{94}{10}\) – \(\frac{38}{10}\) = \(\frac{56}{10}\) = 5\(\frac{6}{10}\) .
Practice
Question 7.
____ = 54 ∗ 10
Answer:
540 = 54 ∗ 10
Explanation :
Any number number multiplied with 10 having single 0 then add one 0 on the right of the number that is 540 .
Question 8.
63 ∗ 100 = ___
Answer:
63 ∗ 100 = 6300 .
Explanation :
Any number number multiplied with 100 having two 0’s then add two 0’s on the right of the number that is 6300 .
Question 9.
86 ∗ 94 = ______
Answer:
86 ∗ 94 = 8,084
Explanation :
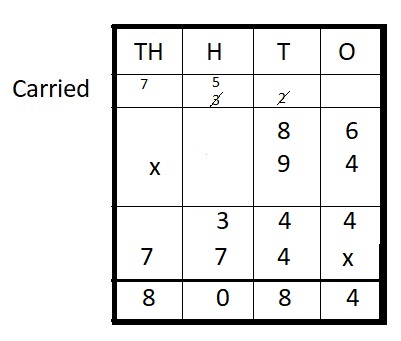
Step I: Arrange the numbers vertically.
Step II: Multiply 86 by 4 ones
86 × 4 = 344
Step III: Multiply 94 by 9 tens
94 × 90 = 7740
Step IV: Add
344 + 7740 = 8084
Question 10.
5,715 ∗ 6 = ___
Answer:
5,715 ∗ 6 = 34,290
Explanation :
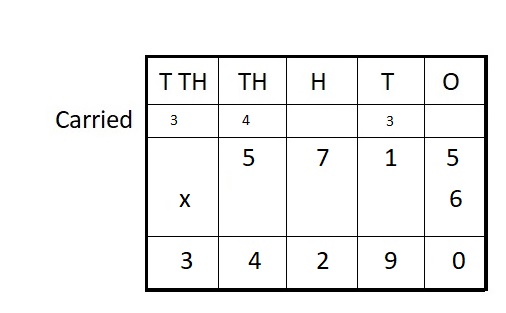 Step I: Arrange the numbers vertically.
Step I: Arrange the numbers vertically.
Step II: First multiply the digit at the ones place by 4.
5 × 6 = 30 = 3 ten + 0 ones
Write 0 in the ones column and carry 3 ten to tens place.
Step III: Multiply the digit at the tens place by 6.
1 × 6 = 6 tens + 3 ( carried ) = 9 tens
Write 9 in ten place
Step IV: Multiply the digit at hundreds place by 6
7 hundred × 6 = 42 hundreds
42 hundreds = 4 thousands + 2 hundreds
Write 2 in hundreds place carry 4 thousands to thousands place.
Step V: Multiply the digit at thousands place by 6.
5 thousands × 6 = 30 thousands
30 + 3 (carried) = 33 thousands = 3 ten thousands + 3 thousands
Write 3 in thousands place and carry 3 ten thousands to ten thousands place.
Everyday Math Grade 4 Home Link 5.9 Answer Key
Student Growth
Mrs. Welch surveyed her students about how much they had grown over the past year. This is the data she gathered.
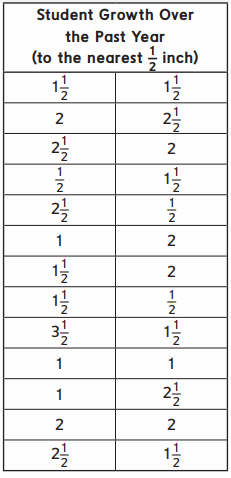
Question 1.
Plot the data set on the line plot.
Answer:
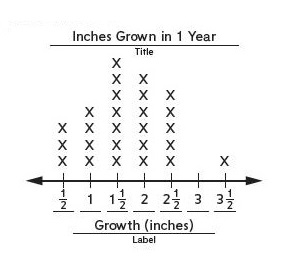
Explanation :
All the students grown height is marked in the graph .
Use the completed line plot to answer the questions.
Question 2.
What is the greatest number of inches a student grew in a year?
About ___ inch(es) The least? ____ About inch(es)
Answer:
3\(\frac{1}{2}\) = Greatest number of inches grown
\(\frac{1}{2}\) = least number of inches grown
Question 3.
What is the difference between the greatest and the least number of inches grown? Number model with unknown: ___ Answer: ____ inch(es)
Answer:
Greatest number of inches grown = 3\(\frac{1}{2}\)
Leastest number of inches grown = 3\(\frac{1}{2}\)
The difference between the greatest and the least number of inches grown =3\(\frac{1}{2}\) – \(\frac{1}{2}\) = 3 .
Practice
Circle the three equivalent fractions in each group.
Question 4.
\(\frac{1}{4}\), \(\frac{3}{6}\), \(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{12}\)
Answer :
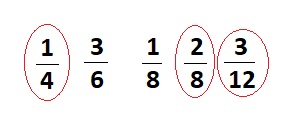
Explanation :
Equivalent fractions are \(\frac{1}{4}\) = \(\frac{2}{8}\) = \(\frac{3}{12}\) .
Question 5.
\(\frac{3}{4}\), \(\frac{4}{8}\), \(\frac{6}{8}\), \(\frac{5}{6}\), \(\frac{9}{12}\)
Answer:
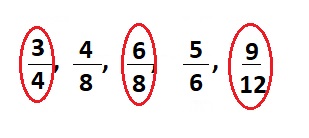
Explanation :
Equivalent fractions are \(\frac{3}{4}\) = \(\frac{6}{8}\) = \(\frac{9}{12}\)
Question 6.
\(\frac{2}{3}\), \(\frac{1}{5}\), \(\frac{4}{6}\), \(\frac{7}{12}\), \(\frac{8}{12}\)
Answer:
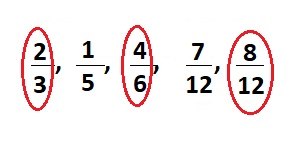
Explanation :
Equivalent fractions are \(\frac{2}{3}\), \(\frac{4}{6}\) and \(\frac{8}{12}\) .
Question 7.
\(\frac{1}{2}\), \(\frac{5}{10}\), \(\frac{4}{8}\), \(\frac{7}{12}\)
Answer:
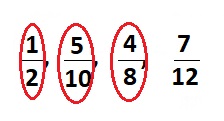
Explanation :
Equivalent fractions are \(\frac{1}{2}\), \(\frac{5}{10}\) and \(\frac{4}{8}\)
Everyday Math Grade 4 Home Link 5.10 Answer Key
Rotations
Family Note If your child needs help with the following problems, consider putting up signs in a room in your home to indicate the directions north, south, east, and west. Do the turns with your child. Please return this Home Link to school tomorrow.
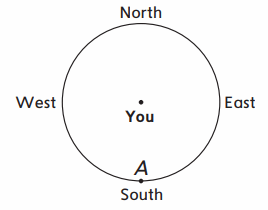
Make the turns described below. Show which way you face after each turn by:
- Drawing a dot on the circle.
- Labeling the dot with a letter.
Example: Face north.
Do a \(\frac{1}{2}\) turn counterclockwise.
On the circle, mark the direction you are facing with the letter A.
Question 1.
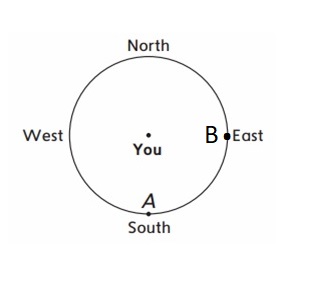
Face north. Do a \(\frac{1}{4}\) turn clockwise. Mark the direction you are facing with the letter B.
Answer:
Question 2.
Face north. Do a \(\frac{3}{4}\) turn clockwise. Mark the direction you are facing with the letter C.
Answer:
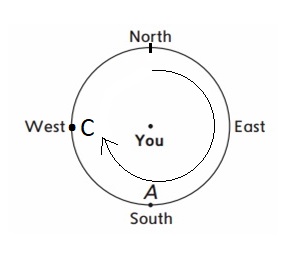
Question 3.
Face east. Do a \(\frac{1}{4}\) turn counterclockwise. Mark the direction you are facing with the letter D.
Answer:
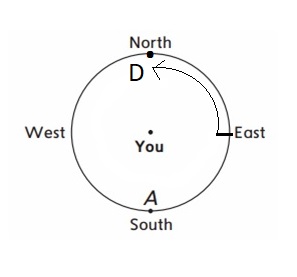
Question 4.
Face west. Make less than a \(\frac{1}{4}\) turn clockwise. Mark the direction you are facing with the letter E.
Answer:
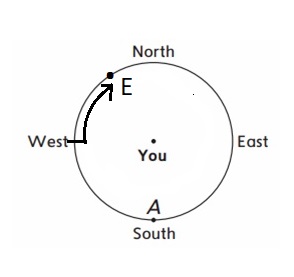
Question 5.
Face north. Make a clockwise turn that is more than a \(\frac{1}{2}\) turn but less than a \(\frac{3}{4}\) turn. Mark the direction you are facing with the letter E.
Answer:
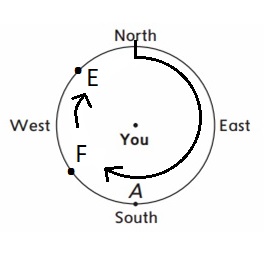
Explanation :
A point is marked between \(\frac{1}{2}\) and \(\frac{3}{4}\) in clockwise direction from North and Point E lies on this clock wise direction towards West .
Question 6.
Face north. Make a counter clock wise turn that is less than a \(\frac{1}{2}\) turn but more than a \(\frac{1}{4}\) turn. Mark the direction you are facing with the letter G.
Answer :
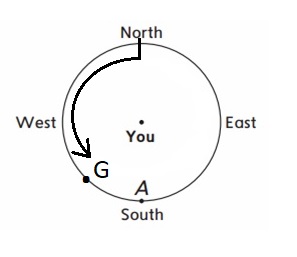
Explanation :
A point is marked between \(\frac{1}{2}\) and \(\frac{1}{4}\) in a counter clock wise direction from North Point G is lies in this direction towards south .
Practice
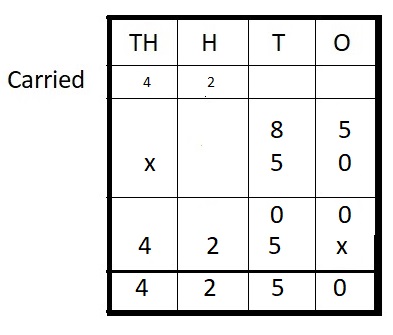
Question 7.
85 ∗ 50 = ___
Answer:
85 ∗ 50 = 4,250
Explanation :
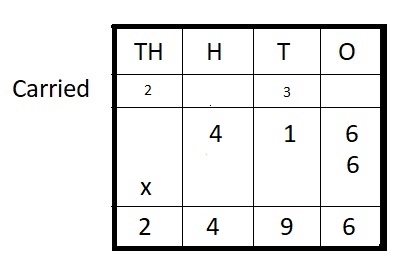
Question 8.
416 ∗ 6 = _____
Answer:
416 ∗ 6 = 2,496
Explanation :
Question 9.
___ = 597 ∗ 4
Answer:
2,376 = 597 ∗ 4
Explanation :
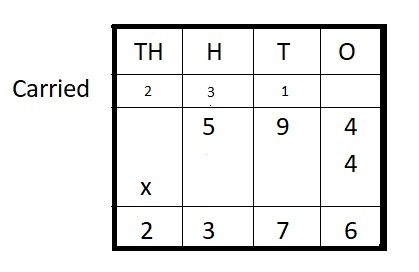
Question 10.
1,373 ∗ 7 = ___
Answer:
1,373 ∗ 7 = 9,611
Explanation :
Everyday Math Grade 4 Home Link 5.11 Answer Key
Estimating Angle Measures
Family Note Our class has been learning about turns, angles, and angle measures. A full turn can be represented by an angle of 360°, a\(\frac{1}{2}\) turn by an angle of 180°, a\(\frac{1}{4}\) turn by an angle of 90°, and so on. Help your child match the measures below with the angles pictured. (It is not necessary to measure the angles with a protractor.)
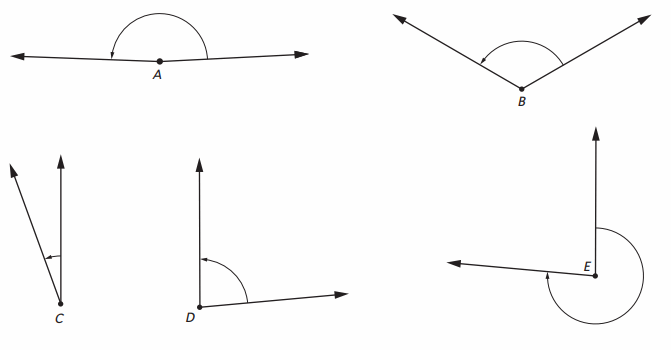
Name which angle has the given measure.
Question 1.
about 180° angle ____
Answer:
Angle A
Question 2.
about 90° angle ____
Answer:
Angle D
Question 3.
about 270° angle ____
Answer:
Angle E
Question 4.
between 0° and 90° angle ___
Answer:
Angle C
Question 5.
between 90° and 180° angle ____
Answer:
Angle A or Angle B

Practice
Question 6.
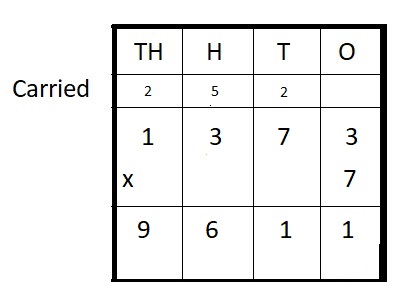
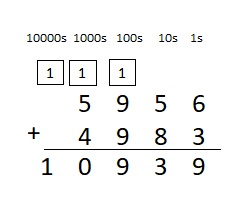
5,956 + 4,983 = ___
Answer:
5,956 + 4,983 = 10,939
Explanation :
Question 7.
60,351 + 86,037 = ___
Answer:
60,351 + 86,037 = 1,46,388
Explanation :
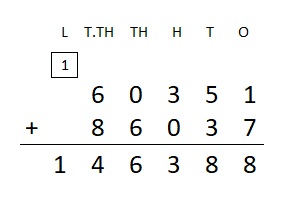
Question 8.
41,015 – 517 = ___
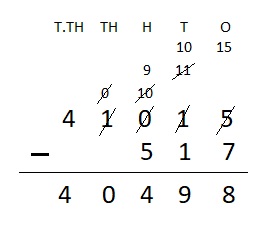
Answer:
41,015 – 517 = 40,498
Explanation :
Question 9.
23,730 – 10,769 = ____
Answer:
23,730 – 10,769 = 12,961
Explanation :
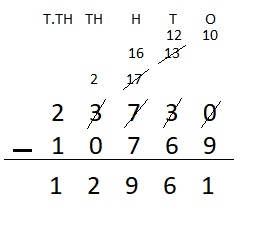
Everyday Math Grade 4 Home Link 5.12 Answer Key
Folding Shapes
Family Note Our class has been studying lines of symmetry—lines that divide figures into mirror images. Help your child look for symmetric shapes in books, newspapers, and magazines, and in objects around the house, such as windows, furniture, dishes, and so on.
Please bring your cutouts to school tomorrow.
Question 1.
Fold a sheet of paper in half. Cut off the folded corner, as shown. Before you unfold the cutoff piece, guess its shape.
a. Unfold the cutoff piece. What shape is it?
________
b. How many sides of the cutoff piece are the same length? sides
c. How many angles are the same size? angles
d. The fold is a line of symmetry. Does the cutoff piece have any other lines of symmetry?
Answer:
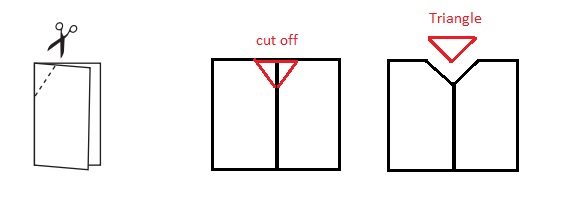
a. The shape of cutoff piece is triangle .
b. 2 sides of the cutoff piece are the same length.
c. 2 angles are the same size .
d. The fold is not a line of symmetry . The cutoff piece doesnot have any other lines of symmetry .
Question 2.
Fold another sheet of paper in half. Fold it in half again. Make a mark on both folded edges 2 inches from the folded corner. Cut off the folded corner. Before you unfold the cutoff piece, guess its shape.
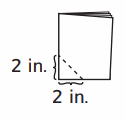
a. Unfold the cutoff piece. What shape is it? ___
b. Are there any other lines of symmetry besides the fold lines?
c. On the back of this paper, draw a picture of the cutoff shape. Draw all of its lines of symmetry.
Answer :
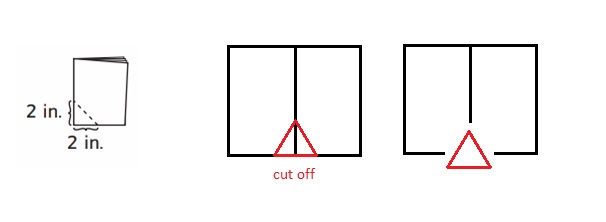
a. The shape of cutoff piece is triangle .
b. No
c. No, lines of symmentry .
Practice
Question 3.
81 ÷ __ = 9
Answer:
81 ÷ 9 = 9
Explanation :
As we know , 9 × 9 = 81
Question 4.
___ ÷ 9 = 6
Answer:
54 ÷ 9 = 6
Explanation :
As we know , 9 × 6 = 54
Question 5.
7 = 42 ÷ ___
Answer:
7 = 42 ÷ 6
Explanation :
As we know , 7 × 6 = 42
Question 6.
___ ÷ 9 = 8
Answer:
72 ÷ 9 = 8
Explanation :
As we know , 9 × 8 = 72
Question 7.
36 ÷ __ = 4
Answer:
36 ÷ 9 = 4
Explanation :
As we know , 9 × 4 = 36
Question 8.
8 = __ ÷ 6
Answer:
8 = 48 ÷ 6
Explanation :
As we know , 8 × 6 = 48
Everyday Math Grade 4 Home Link 5.13 Answer Key
Expressing Answers to Number Stories
Family Note Today students learned to express solutions to multistep number stories using correct units and single number models. Have your child explain the steps for solving each of the problems below, and then help him or her write these steps as a single number model, including a letter for the unknown quantity.
Solve. Record a long number model with a letter for the unknown quantity and write the answer with the correct unit.
Question 1.
Guillermo hires two painters to paint the walls of his living room. The painters each make $42 an hour for an 8-hour workday. If the work takes 3 days, how much will Guillermo pay the painters?
Number model with unknown: ___________
Estimate: __________
Answer (with unit): ________
Answer:
Number of Painters = 2
Number of Hours painted for 1 day = 8 hours
Number of hours painted for 3 days = 8 × 3 = 24 hours
Number of hours painted by 2 painters = 2 × 24 = 48 hours
Cost of one hour to paint = $42
Cost of 48 hours to paint = $42 × 48 = 2016 $
Estimation:
Number of hours painted by 2 painters = 2 × 24 = 48 hours ==>50 hours
Cost of one hour to paint = $42 ==>40
Cost of 48 hours to paint = $40 × 50 = 2000 $
Question 2.
Blaine is on vacation in New York City and wants to collect magnets of places he visits to give to all his friends. The Times Square magnets cost $2 each and come in sets of 4. The Statue of Liberty magnets cost $3 each and come in sets of 5.
If Blaine buys 12 sets of each type of magnet, how much will he pay?
Number model with unknown: _______
Estimate: ______
Answer (with unit): ______
Cost of Each Times Square Magnets = $2
Number in one set= 4
Cost of each set = $2 × 4 = $8
Cost of 12 sets of Times and Square Magnets = $8 × 12 = 96 $
Cost of Each Statue of Liberty Magnets = $3
Number in one set= 5
Cost of each set = $3 × 5 = $15
Cost of 12 sets of Statue of Liberty Magnets = $15 × 12 = 180 $
Total cost = 96 + 180 = 276 $
Estimation:
Cost of 12 sets of Times and Square Magnets = $8 × 12 = 96 $ ==>100$
Cost of 12 sets of Statue of Liberty Magnets = $15 × 12 = 180 $
Total cost = 100 + 180 = 280$
Practice
Question 3.
45 ÷ 5 = ___
Answer:
45 ÷ 5 = 9
Explanation :
As we know , 9 × 5 = 45
Question 4.
56 ÷ 8 = ___
Answer:
56 ÷ 8 = 7
Explanation :
As we know , 8 × 7 = 56
Question 5.
54 ÷ 9 = ___
Answer:
54 ÷ 9 = 6
Explanation :
As we know , 9 × 6 = 54
Question 6.
__ ÷ 9 = 4
Answer:
36 ÷ 9 = 4
Explanation :
As we know , 9 × 4 = 36
Question 7.
__ ÷ 6 = 6
Answer:
36 ÷ 6 = 6
Explanation :
As we know , 6 × 6 = 36
Question 8.
__ ÷ 8 = 3
Answer:
24 ÷ 8 = 3
Explanation :
As we know , 8 × 3 = 24