Everyday Math Grade 4 Answers Unit 3 Fractions and Decimals

Everyday Mathematics 4th Grade Answer Key Unit 3 Fractions and Decimals

Everyday Math Grade 4 Home Link 3.1 Answer Key

Sharing Equally

Use drawings to help you solve the problems. Solve each problem in more than one way. Show your work.

Question 1.
Four friends shared 5 pizzas equally. How much pizza did each friend get?
____ pizzas
One way:

Another way:
Answer:

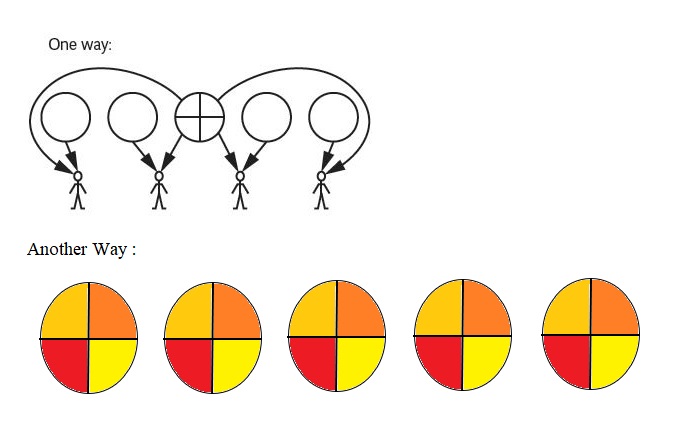
Explanation :
First Way :
Number of Pizzas = 5
Number of people = 4
Each Person take a pizza, number of pizzas taken = 4 pizzas
Number of pizzas left = 1
Fraction of pizza each person get = \(\frac{1}{4}\).
Fraction of pizza each person get = 1 + \(\frac{1}{4}\) = \(\frac{5}{4}\) .

Second Way :
Number of Pizzas = 5
Number of people = 4
Each pizza is divided into 4 parts .
Each person takes 1 pizza slice .
Fraction of each pizza slice = \(\frac{1}{4}\)
Total Fraction of 5 pizza slices = 5 × \(\frac{1}{4}\) = \(\frac{5}{4}\)
Therefore , Each person gets \(\frac{5}{4}\) fraction of pizza that means each person gets 1 slice from 5 pizzas .
it is represented in above figure with different colors .

Question 2.
Five kittens are sharing 6 cups of milk equally. How much milk does each kitten get?
____ cups of milk
One way:

Another way:
Answer:
One Way :
Number of Kittens = 5
Number of cups of milk = 6
Each kittens gets 1 cup that means 5 cups of milk is given to 5 kittens .
1 cup of milk is left which is shared by 5 kittens .
Fraction of milk given to each kitten in 1 cup = number of cups  ÷ number of kittens = 1 ÷ 5 =
Total cups of milk given each kitten = 1 + \(\frac{1}{5}\) = \(\frac{5}{5}\) + \(\frac{1}{5}\) = \(\frac{6}{5}\) cups .
Another Way :
Number of Kittens = 5
Number of cups of milk = 6
Each cup of milk is divided into 5 parts .
Each kitten is given \(\frac{1}{5}\)  cup of milk
As there are 6 cups Each kitten gets 6 × \(\frac{1}{5}\)  cup of milk = \(\frac{6}{5}\) cups of milk .
Therefore each kitten gets \(\frac{6}{5}\) cups of milk .

Practice

Question 3.
Name the next 4 multiples of 7. 7, ___, ___, ___, ___
Answer:
The next 4 multiples of 7 are :
7, 14, 21, 28 .

Question 4.
List all the factors of 18. ____
Answer:
All factors of 18 are : 1, 2, 3, 6, 9 , 18 .

Question 5.
List all the factors of 18 that are prime.
Answer:
All factors of 18 are : 1, 2, 3, 6, 9 , 18 .
All factors of 18 that are prime  : 1, 2, 3 .
Explanation :
A number that is divisible only by itself and 1 (e.g. 2, 3, 5, 7, 11).

Question 6.
List all the factor pairs of 40.
___ and ___; ___ and ; ___
___ and ___; ___ and ; ___
Answer:
The  pair factors of 40 are (1, 40), (2, 20), (4, 10), and (5, 8).

Everyday Math Grade 4 Home Link 3.2 Answer Key

Fraction Circles

Question 1.
Divide into 4 equal parts. Shade \(\frac{1}{4}\).

Answer:

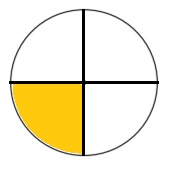
Explanation :
Circle is divided into 4 parts . Each part is a fraction of \(\frac{1}{4}\) and and 1 part is shaded .

Question 2.
Divide into 8 equal parts. Shade \(\frac{2}{8}\).

Answer:

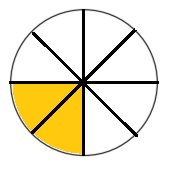
Explanation :
Circle is divided into 8 parts . Each part is a fraction of \(\frac{1}{8}\) and and 2 parts are shaded .

Question 3.
Divide into 12 equal parts. Shade \(\frac{3}{12}\).

Answer:

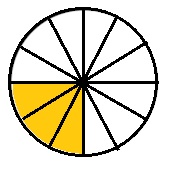
Explanation :
Circle is divided into 12 parts . Each part is a fraction of \(\frac{1}{12}\) and and 3 parts are shaded .

Question 4.
Create your own. Divide into equal parts and shade a portion. Record the amount you shaded.

Answer:

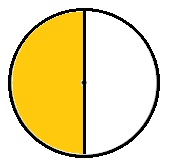
Explanation :
Circle is divided into 2 parts . Each part is a fraction of \(\frac{1}{2}\) and 1 part is shaded which is a fraction of \(\frac{1}{2}\)  .

Question 5.
What patterns do you notice in Problems 1 through 3?
Answer:
The pattern we notice in problem 1 through 3 is equivalent fraction .
\(\frac{1}{4}\) = \(\frac{2}{8}\) = \(\frac{3}{12}\) .

Practice

Question 6.
List the next 4 multiples of 5. 20, __, ___, ___, ___
Answer:
4 multiples of 5 are from 20 , 25, 30, 35, 40 .

Question 7.
List all the factors of 48. __________
Answer:
All Factors of 48 are : 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.

Question 8.
List the factors of 48 that are composite. __________
Answer:
All Factors of 48 are : 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.
composite numbers are :  4, 6, 8, 12, 16, 24 and 48.
Explanation :
A composite number is a natural number or a positive integer which has more than two factors. For example, 15 has factors 1, 3, 5 .

Everyday Math Grade 4 Home Link 3.3 Answer Key

Finding Equivalent Fractions

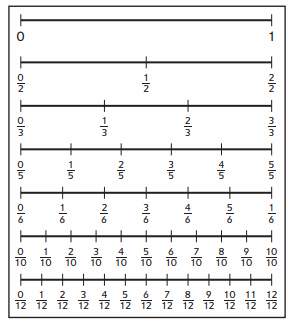
Use the number lines to help you answer the following questions

1 . Fill in the blank with = or ≠ .
a. \(\frac{2}{3}\) __ \(\frac{1}{3}\)
Answer:
\(\frac{2}{3}\) > \(\frac{1}{3}\)

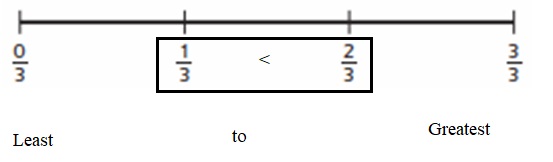
Explanation :
1. A fraction is larger if it’s farther from 0 on the number line.
2. A fraction is smaller if it’s closer to 0 on the number line.
\(\frac{2}{3}\) is farther from 0 so, it is greater number .
Therefore, \(\frac{2}{3}\) > \(\frac{1}{3}\) .

b. \(\frac{2}{6}\) ____ \(\frac{1}{3}\)
Answer:
\(\frac{2}{6}\) =  \(\frac{1}{3}\)

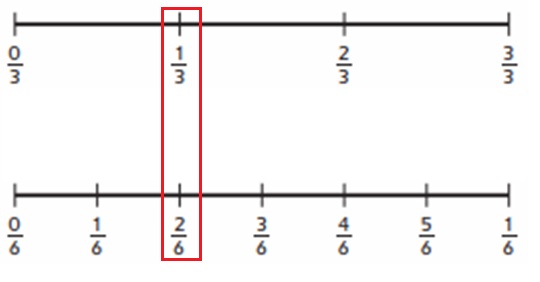
Explanation :
\(\frac{2}{6}\) = \(\frac{1}{3}\) as both locate at the same point as shown in above figure .

c. \(\frac{2}{6}\) __ \(\frac{2}{5}\)
Answer:
\(\frac{2}{5}\) > \(\frac{2}{6}\)

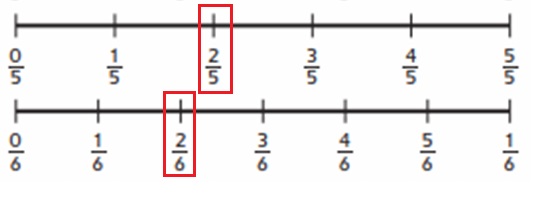
Explanation :
1. A fraction is larger if it’s farther from 0 on the number line.
2. A fraction is smaller if it’s closer to 0 on the number line.
\(\frac{2}{5}\) is farther from 0 than \(\frac{2}{6}\) so, it is a greater number
Therefore, \(\frac{2}{5}\) > \(\frac{2}{6}\) .

d. \(\frac{1}{5}\) ___ \(\frac{2}{10}\)
Answer:

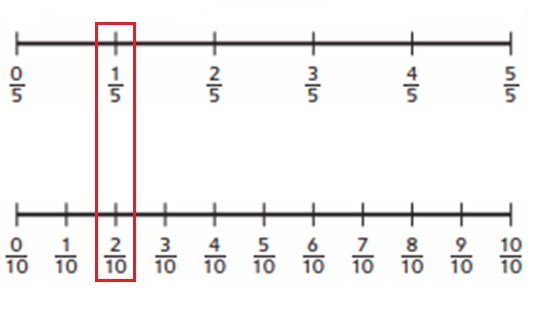
Explanation :
\(\frac{2}{6}\) = \(\frac{1}{3}\) as both locate at the same point as shown in above figure .

Question 2.
Fill in the missing numbers.
a.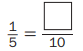
Answer:
\(\frac{1}{5}\) = \(\frac{2}{10}\)
Explanation :
The fraction \(\frac{1}{5}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 1 by 2, the result is 2. When you multiply the denominator 5 by 2, the result is 10.
\(\frac{1 \times 2}{5 \times 2}\) = \(\frac{2}{10}\)
This results in the number sentence \(\frac{1}{5}\) = \(\frac{2}{10}\).

b.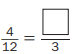
Answer:
\(\frac{4}{12}\) = \(\frac{1}{3}\)
Explanation :
The fraction \(\frac{4}{12}\) can be renamed as an infinite number of equivalent fractions.
When you divide the numerator 4 by 4, the result is 1. When you divide the denominator 12 by 4, the result is 3.
\(\frac{4  ÷ 4 }{12 ÷ 4 }\)= \(\frac{1}{3}\)
This results in the number sentence \(\frac{4}{12}\) = \(\frac{1}{3}\).

c.
Answer:
\(\frac{5}{10}\) = \(\frac{1}{2}\)
Explanation :
The fraction \(\frac{5}{10}\) can be renamed as an infinite number of equivalent fractions.
When you divide the numerator 5 by 5, the result is 1. When you divide the denominator 10 by 5, the result is 2.
\(\frac{5  ÷ 5 }{10 ÷ 5 }\)= \(\frac{1}{2}\)
This results in the number sentence \(\frac{5}{10}\) = \(\frac{1}{2}\).

d.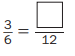
Answer:
\(\frac{3}{6}\) = \(\frac{6}{12}\)
Explanation :
The fraction \(\frac{3}{6}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 3 by 2, the result is 6. When you multiply the denominator 6 by 2, the result is 12.
\(\frac{3 \times 2}{6 \times 2}\) = \(\frac{6}{12}\)
This results in the number sentence \(\frac{3}{6}\) = \(\frac{6}{12}\).

e.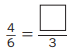
Answer:
\(\frac{4}{6}\) = \(\frac{2}{3}\)
Explanation :
The fraction \(\frac{4}{6}\) can be renamed as an infinite number of equivalent fractions.
When you divide the numerator 4 by 2, the result is 2. When you divide the denominator 6 by 2, the result is 3.
\(\frac{4  ÷ 2 }{6 ÷ 2 }\)= \(\frac{2}{3}\)
This results in the number sentence \(\frac{4}{6}\) = \(\frac{2}{3}\).

Question 3.
Circle the number sentences that are NOT true.
a. \(\frac{3}{12}\) = \(\frac{1}{4}\)
Answer:
Yes, it is true
\(\frac{3}{12}\) = \(\frac{1}{4}\)
Explanation :
The fraction \(\frac{3}{12}\) can be renamed as an infinite number of equivalent fractions.
When you divide the numerator 3 by 3, the result is 1. When you divide the denominator 12 by 3, the result is 4.
\(\frac{3  ÷ 3 }{12 ÷ 3 }\)= \(\frac{1}{4}\)
This results in the number sentence \(\frac{3}{12}\) = \(\frac{1}{4}\).

b. \(\frac{1}{2}\) = \(\frac{5}{10}\)
Answer:
Yes, it is true
\(\frac{1}{2}\) = \(\frac{5}{10}\)
Explanation :
The fraction \(\frac{1}{2}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 1 by 5, the result is 5. When you multiply the denominator 2 by 5, the result is 10.
\(\frac{1 \times 5}{2 \times 5}\) = \(\frac{5}{10}\)
This results in the number sentence \(\frac{1}{2}\) = \(\frac{5}{10}\).

c. \(\frac{2}{6}\) = \(\frac{2}{5}\)
Answer:
No it is not true \(\frac{2}{6}\) can’t be equal to  \(\frac{2}{5}\)

d. \(\frac{7}{10}\) = \(\frac{4}{6}\)
Answer:
No it is not true \(\frac{7}{10}\) can’t be equal to  \(\frac{4}{6}\)

e. \(\frac{9}{10}\) = \(\frac{11}{12}\)
Answer:
No it is not true \(\frac{9}{10}\) can’t be equal to  \(\frac{11}{12}\)

Practice

Solve using U.S. traditional addition or subtraction.

Question 4.
____ = 989 + 657
Answer:
1646 = 989 + 657

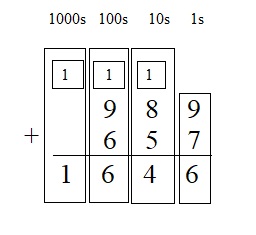
Explanation :

Step 1
Add the 1s: 9 + 7 = 16.
16 ones = 1 ten and 6 ones
Write 1 in the 6s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 8 + 5 + 1 = 14
14 tens = 1 hundred + 4 tens
Write 4 in the 10s place below the line.
Write 1 above the digits in the 100s place.

Step 3
Add the 100s: 9 + 6 + 1 = 16
16 hundreds = 1 thousand + 6 hundred
Write 6 in the 100s place below the line.
Write 1 above the digits in the 1000s place.
No values to add in the thousand’s place so write 1 below the line in 1000s place .

Question 5.
3,314 + 4,719 = ____
Answer:
3,314 + 4,719 = 8033

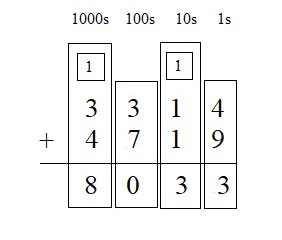
Explanation :

Step 1
Add the 1s: 4 + 9 = 13.
13 ones = 1 ten and 3 ones
Write 3 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 1 + 1 + 1 = 3
Write 3 in the 10s place below the line.

Step 3
Add the 100s: 3 + 7  = 10
10 hundreds = 1 thousand + 0 hundred
Write 0 in the 100s place below the line.
Write 1 above the digits in the 1000s place.

Step 4
Add the 1000s: 3 + 4 + 1 = 8
Write 8 in the 1000s place below the line.

Question 6.
5,887 – 3,598 = ___
Answer:
5,887 – 3,598 = 2289

Question 7.
____ = 2,004 – 1,716
Answer:
288= 2,004 – 1,716

Everyday Math Grade 4 Home Link 3.4 Answer Key

Finding Equivalent Fractions

Family Note Today students learned about an Equivalent Fractions Rule, which can be used to rename any fraction as an equivalent fraction. The rule for multiplication states that if the numerator and denominator are multiplied by the same nonzero number, the result is a fraction that is equivalent to the original fraction.
For example, the fraction \(\frac{1}{2}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 1 by 5, the result is 5. When you multiply the denominator 2 by 5, the result is 10.
\(\frac{1 \times 5}{2 \times 5}\) = \(\frac{5}{10}\)
This results in the number sentence \(\frac{1}{2}\) = \(\frac{5}{10}\). If you multiplied both the numerator and denominator in \(\frac{1}{2}\) by 3, the result would be \(\frac{3}{6}\), which is also equal to \(\frac{1}{2}\).

Fill in the boxes to complete the equivalent fractions.

Example: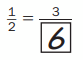

Question 1.

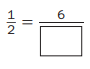
Answer:
\(\frac{1}{2}\) = \(\frac{6}{12}\)
Explanation :
The fraction \(\frac{1}{2}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 1 by 6, the result is 6. When you multiply the denominator 2 by 6, the result is 12.
\(\frac{1 \times 6}{2 \times 6}\) = \(\frac{6}{12}\)
This results in the number sentence \(\frac{1}{2}\) = \(\frac{6}{12}\).

Question 2.

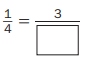
Answer:
\(\frac{1}{4}\) = \(\frac{3}{12}\)
Explanation :
The fraction \(\frac{1}{4}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 1 by 3, the result is 3. When you multiply the denominator 4 by 3, the result is 12.
\(\frac{1 \times 3}{4 \times 3}\) = \(\frac{3}{12}\)
This results in the number sentence \(\frac{1}{4}\) = \(\frac{3}{12}\).

Question 3.

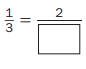
Answer:
\(\frac{1}{3}\) = \(\frac{2}{6}\)
Explanation :
The fraction \(\frac{1}{3}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 1 by 2, the result is 2. When you multiply the denominator 3 by 2, the result is 6.
\(\frac{1 \times 2}{3 \times 2}\) = \(\frac{2}{6}\)
This results in the number sentence \(\frac{1}{3}\) = \(\frac{2}{6}\).

Question 4.

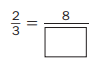
Answer:
\(\frac{2}{3}\) = \(\frac{8}{12}\)
Explanation :
The fraction \(\frac{2}{3}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 2 by 4, the result is 8. When you multiply the denominator 3 by 4, the result is 12.
\(\frac{2 \times 4}{3 \times 4}\) = \(\frac{8}{12}\)
This results in the number sentence \(\frac{2}{3}\) = \(\frac{8}{12}\).

Question 5.

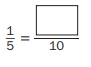
Answer:
\(\frac{1}{5}\) = \(\frac{2}{10}\)
Explanation :
The fraction \(\frac{1}{5}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 1 by 2, the result is 2. When you multiply the denominator 5 by 2, the result is 10.
\(\frac{1 \times 2}{5 \times 2}\) = \(\frac{2}{10}\)
This results in the number sentence \(\frac{1}{5}\) = \(\frac{2}{10}\).

Question 6.

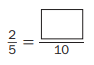
Answer:
\(\frac{2}{5}\) = \(\frac{4}{10}\)
Explanation :
The fraction \(\frac{2}{5}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 2 by 2, the result is 4. When you multiply the denominator 5 by 2, the result is 10.
\(\frac{2 \times 2}{5 \times 2}\) = \(\frac{4}{10}\)
This results in the number sentence \(\frac{2}{5}\) = \(\frac{4}{10}\).

Question 7.

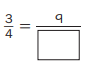
Answer:
\(\frac{3}{4}\) = \(\frac{9}{12}\)
Explanation :
The fraction \(\frac{3}{4}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 3 by 3, the result is 9. When you multiply the denominator 4 by 3, the result is 12.
\(\frac{3 \times 3}{4 \times 3}\) = \(\frac{9}{12}\)
This results in the number sentence \(\frac{3}{4}\) = \(\frac{9}{12}\).

Question 8.

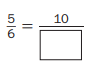
Answer:
\(\frac{5}{6}\) = \(\frac{10}{12}\)
Explanation :
The fraction \(\frac{5}{6}\) can be renamed as an infinite number of equivalent fractions.
When you multiply the numerator 5 by 2, the result is 10. When you multiply the denominator 6 by 2, the result is 12.
\(\frac{5 \times 2}{6 \times 2}\) = \(\frac{10}{12}\)
This results in the number sentence \(\frac{5}{6}\) = \(\frac{10}{12}\).

Question 9.

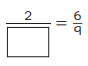
Answer:
\(\frac{6}{9}\) = \(\frac{2}{3}\)
Explanation :
The fraction \(\frac{6}{9}\) can be renamed as an infinite number of equivalent fractions.
When you divide the numerator 6 by 3, the result is 2. When you divide the denominator 9 by 3, the result is 3.
\(\frac{6  ÷ 3 }{9 ÷ 3 }\)= \(\frac{2}{3}\)
This results in the number sentence \(\frac{2}{3}\) = \(\frac{6}{9}\).

Question 10.

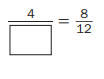
Answer:
\(\frac{4}{6}\) = \(\frac{8}{12}\)
Explanation :
The fraction \(\frac{8}{12}\) can be renamed as an infinite number of equivalent fractions.
When you divide the numerator 8 by 2, the result is 4. When you divide the denominator 12 by 2, the result is 6.
\(\frac{8  ÷ 2 }{12 ÷ 2 }\)= \(\frac{4}{6}\)
This results in the number sentence \(\frac{4}{6}\) = \(\frac{8}{12}\).

Question 11.
Name 3 equivalent fractions for \(\frac{1}{2}\). ___
Answer:
The fraction \(\frac{8}{12}\) can be renamed as an infinite number of equivalent fractions.
The 3 equivalent fractions for \(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) .

Practice

Question 12.
List all the factors of 56.
Answer:
Factors of 56: 1, 2, 4, 7, 8, 14, 28 and 56

Question 13.
Write the factor pairs for 30.
___ and ___, ____ and ___, ___ and, ___.
___ and ____
Answer:
The factor pairs for 30 are 2 and 15, 3 and 10, 5 and 6 , 1 and 30 .

Question 14.
Is 30 prime or composite? ____
Answer:
30 is a Composite .
Explanation :
A composite number is a number that can be divided evenly by more numbers than 1 and itself. It is the opposite of a prime number. The number 30 can be evenly divided by 1 2 3 5 6 10 15 and 30, with no remainder. Since 30 cannot be divided by just 1 and 30, it is a composite number.

Everyday Math Grade 4 Home Link 3.5 Answer Key

Sharing Veggie Pizza

Question 1.
Karen and her 3 friends want to share 3 small veggie pizzas equally. Karen tried to figure out how much pizza each of the 4 children would get. She drew this picture and wrote two answers.
a. Which of Karen’s answers is correct? ___
b. Draw on Karen’s diagram to make it clear how the pizza should be distributed among the 4 children.

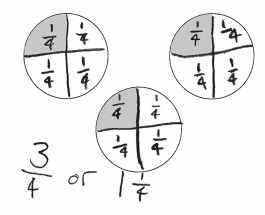
Answer:
a. \(\frac{3}{4}\) is the correct answer .
b.
Number of children = 4
Number of pizzas = 3
Each Pizza is divided into 4 parts. Each children get \(\frac{1}{4}\) part of pizza .
Fraction of pizza received by each children from 3 pizzas= 3 × \(\frac{1}{4}\) part of pizza . = \(\frac{3}{4}\)
Each children get respective number written on pizzas as shown in below diagram .

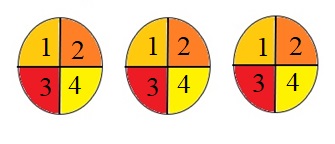
Question 2.
Erin and her 7 friends want to share 6 small veggie pizzas equally. How much pizza will each of the 8 children get ? ___
Answer:
Erin and here $7$ friends are sharing pizza
$\Rightarrow 8$ people are sharing pizza.
$6$ pizzas divided among $8$ people:
Fraction of pizza each children get = \(\frac{6 pizzas }{8 people}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\) .
That means 4 children share 3 pizzas .
Each Pizza is divided into 4 parts. Each children get \(\frac{1}{4}\) part of pizza .
Fraction of pizza received by each children from 3 pizzas= 3 × \(\frac{1}{4}\) part of pizza . = \(\frac{3}{4}\)
Each children get respective number written on pizzas as shown in below diagram .

Question 3.
Who will get more pizza, Karen or Erin? ____ Explain or show how you know.
Answer :
Both Karen and Erin gets same amount of Pizza that is \(\frac{3}{4}\) of the pizza .

Practice

Question 4.
List all the factors of 50. __________
Answer:
Factors of 50 : 1, 2, 5, 10 and 50 .

Question 5.
Is 50 prime or composite? __________
Answer:
50 is a composite number .
Explanation :
A composite number is a number that can be divided evenly by more numbers than 1 and itself. … The number 50 can be evenly divided by 1, 2, 5, 10, 25 and 50, with no remainder. Since 50 cannot be divided by just 1 and 50, it is a composite number

Question 6.
Write the factor pairs for 75.
___ and ___
___ and ___
___ and ___
Answer :
The factor pairs for 75 are
3 and 25.
5 and 15.
1 and 75 .

Everyday Math Grade 4 Home Link 3.6 Answer Key

Solving Fraction Comparison Number Stories

Solve the problems below.

Question 1.
Tenisha and Christa were each reading the same book. Tenisha said she was \(\frac{3}{4}\) of the way done with it, and Christa said she was \(\frac{6}{8}\) of the way finished. Who has read more, or have they read the same amount? Ho w do you know?
Answer:
Fraction of book read by Tenisha = \(\frac{3}{4}\)
Fraction of book read by christa = \(\frac{6}{8}\) = \(\frac{3}{4}\) .
\(\frac{3}{4}\) = \(\frac{6}{8}\)
Explanation :
The fraction \(\frac{6}{9}\) can be renamed as an infinite number of equivalent fractions.
When you divide the numerator 6 by 2, the result is 3. When you divide the denominator 8 by 2, the result is 4.
\(\frac{6  ÷ 2 }{8 ÷ 2 }\)= \(\frac{3}{4}\)
This results in the number sentence \(\frac{3}{4}\) = \(\frac{6}{8}\).

Question 2.
Heather and Jerry each bought an ice cream bar. Although the bars were the same size, they were different flavors. Heather ate \(\frac{5}{8}\) of her ice cream bar, and Jerry ate \(\frac{5}{10}\) of his.
Who ate more, or did they eat the same amount? ___
Write a number sentence to show this. ___
Answer :

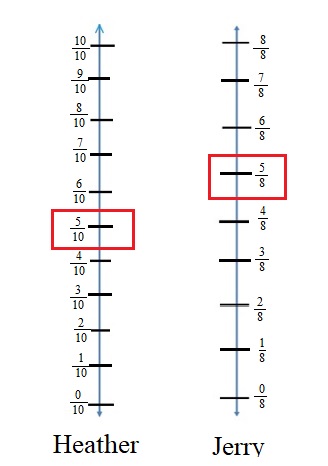
Explanation :
Fraction of ice cream ate by Heather = \(\frac{5}{8}\)
Fraction of ice cream ate by Jerry = \(\frac{5}{10}\)
Both the ice creams bar are represented in the above figure .
from the above figure we notice that \(\frac{5}{8}\) > \(\frac{5}{10}\) that means Jerry ate more ice cream bar than Heather .

Question 3.
Howard’s baseball team won \(\frac{7}{10}\) of its games. Jermaine’s team won \(\frac{2}{5}\) of its games. They both played the same number of games.
Whose team won more games, or did they win the same amount? ___
How do you know? __________
Answer:

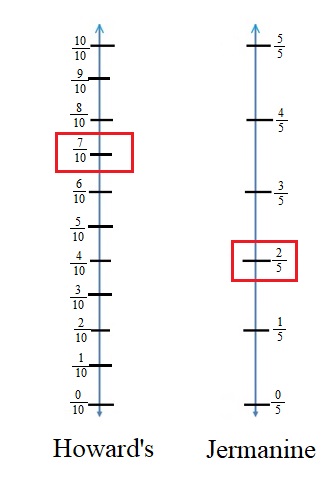
Fraction of games won by Howard’s = \(\frac{7}{10}\)
Fraction of games won by Jermaine’s = \(\frac{2}{5}\)
\(\frac{7}{10}\)  >\(\frac{2}{5}\)  that means Howard won more games than Jermaine as it shown in the above figure .

Question 4.
Write your own fraction number story. Ask someone at home to solve it.
Answer:
Cristine had 4/5 m of cloth. She used 3/4 of it to make handkerchiefs. How much cloth had she left?
Explanation :
Fraction of total cloth with Cristine = \(\frac{4}{5}\) m
Fraction of cloth used = \(\frac{3}{4}\) m
Fraction of cloth left = \(\frac{4}{5}\)  – \(\frac{3}{4}\) m = \(\frac{16}{20}\)  – \(\frac{15}{20}\) = \(\frac{1}{20}\) m .
Therefore, Fraction of cloth left = \(\frac{1}{20}\) m .

Practice

Write T for true or F for false.

Question 5.
1,286 + 2,286 = 3,752 ___
Answer:
1,286 + 2,286 = 3,752 is not true as
Explanation :
1,286 + 2,286 = 3,572

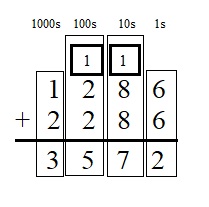
Question 6.
9,907 – 9,709 = 200 ___
Answer:
9,907 – 9,709 = 200 is not true as 9,907 – 9,709 = 198 .
Explanation :

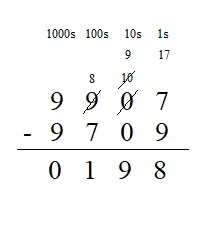
Question 7.
2,641 + 4,359 = 2,359 + 4,641 ___
Answer:
2,641 + 4,359 = 2,359 + 4,641 yes, it is true .
Explanation :

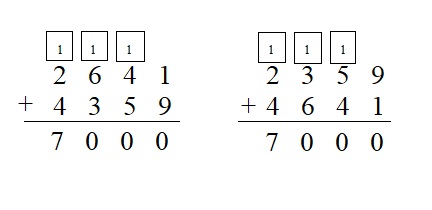
Question 8.
2,345 – 198 = 2,969 – 822 ____
Answer:
2,345 – 198 = 2,969 – 822 Yes, it is true .
Explanation :

Everyday Math Grade 4 Home Link 3.7 Answer Key

Comparing and Ordering Fractions

Write the fractions from smallest to largest, and then justify your conclusions by placing the numbers in the correct places on the number lines.

Question 1.

Answer:

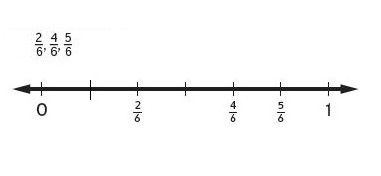
Explanation :
1. A fraction is larger if it’s farther from 0 on the number line.
2. A fraction is smaller if it’s closer to 0 on the number line.
\(\frac{5}{6}\) is farther from 0 so, it is greater number .
\(\frac{2}{6}\) is closer to 0 so, it is smaller number .
Therefore, \(\frac{2}{6}\) < \(\frac{4}{6}\)  < \(\frac{5}{6}\) .

Question 2.

Answer:

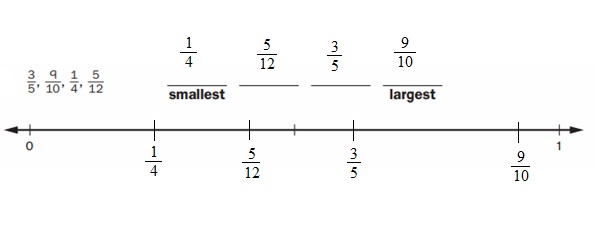
Explanation :
1. A fraction is larger if it’s farther from 0 on the number line.
2. A fraction is smaller if it’s closer to 0 on the number line.
\(\frac{9}{10}\) is farther from 0 so, it is greater number .
\(\frac{1}{4}\) is closer to 0 so, it is smaller number .
Therefore, \(\frac{1}{4}\) < \(\frac{5}{12}\)  < \(\frac{3}{5}\) < \(\frac{9}{10}\) .

Question 3.

Answer:

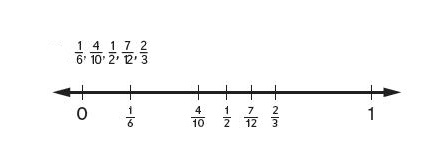
Explanation :
1. A fraction is larger if it’s farther from 0 on the number line.
2. A fraction is smaller if it’s closer to 0 on the number line.
\(\frac{2}{3}\) is farther from 0 so, it is greater number .
\(\frac{1}{6}\) is closer to 0 so, it is smaller number .
Therefore, \(\frac{1}{6}\) < \(\frac{4}{10}\)  < \(\frac{1}{2}\) < \(\frac{7}{12}\) < \(\frac{2}{3}\) .

Practice

Question 4.
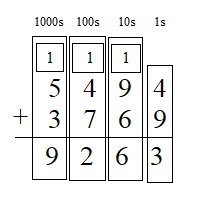
___ = 5,494 + 3,769
Answer:
9263 = 5,494 + 3,769
Explanation :

Question 5.
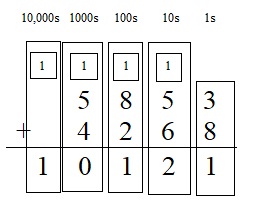
5,853 + 4,268 = ___
Answer:
5,853 + 4,268 = 10,121
Explanation :

Question 6.
__ = 8,210 – 6,654
Answer:
1556 = 8,210 – 6,654
Explanation :

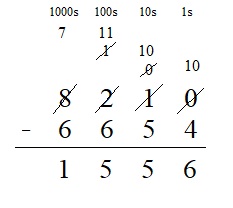
Question 7.
7,235 – 5,906 = ___
Answer:
7,235 – 5,906 = 1329
Explanation :

Everyday Math Grade 4 Home Link 3.8 Answer Key

Names for Fractions and Decimals

Question 1.
Fill in the blanks in the table below.

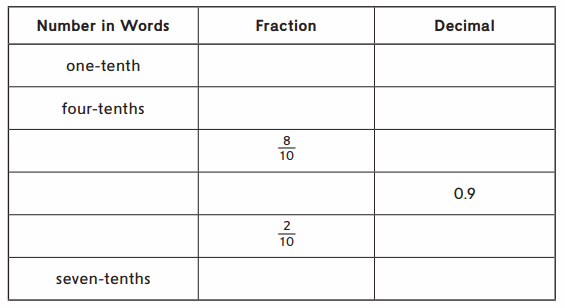
Answer:

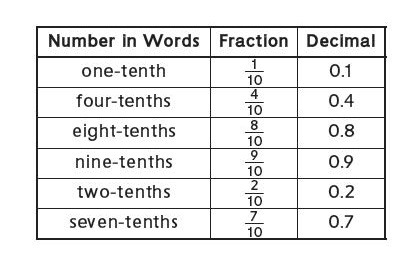
Question 2.
Name two ways you might see decimals used outside of school.

Answer:
The Two ways we see decimals used outside of school are Money and to represent Weight .

Question 3.
What decimal is represented by the tick mark labeled M?
Answer:

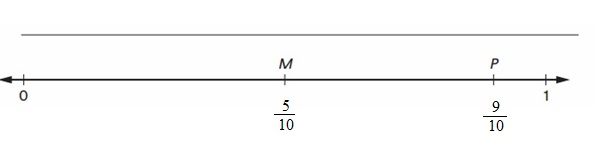
The M and P are marked as per given table which in the fractions of 10 .
The fraction of tick Mark labeled M =  \(\frac{5}{10}\)  = 0.5

Question 4.
What fraction is represented by the tick mark labeled M?
Answer:
The fraction of tick Mark labeled M =  \(\frac{5}{10}\)

Question 5.
What decimal is represented by the tick mark labeled P?
Answer:
The M and P are marked as per given table which in the fractions of 10 .
The fraction of tick Mark labeled P =  \(\frac{9}{10}\)  = 0.9

Question 6.
What fraction is represented by the tick mark labeled P?
Answer:
The fraction of tick Mark labeled P =  \(\frac{9}{10}\)

Practice

Question 7.
List all the factors of 100.
Answer:
The Factors of 100 : 1, 2, 4, 5, 10, 20, 25, 50, and 100

Question 8.
List the factors of 100 that are prime.
Answer:
The Factors of 100 : 1, 2, 4, 5, 10, 20, 25, 50, and 100
where 2 and 5 are the prime numbers.
Explanation :
Prime numbers are special numbers, greater than 1, that have exactly two factors, themselves and 1.

Question 9.
Write the factor pairs for 42.
___ and ___ ___and ___
___ and ___ ___and ___
Answer :
The factor pairs for 42 are
2 and 21.
3 and 14 .
6 and 7 .

Everyday Math Grade 4 Home Link 3.9 Answer Key

Representing Fractions and Decimals

If the grid is the whole, then what part of each grid is shaded?
Write a fraction and a decimal below each grid.

Question 1.

fraction: __________
decimal: __________
Answer:
Total Number of boxes = 100
Number of boxes shaded = 30 .
Fraction = Number of boxes shaded by Total Number of boxes in a grid .
fraction: \(\frac{30}{100}\)
decimal: 0.30
Explanation :
Division by 10, 100 ,1000, etc. Shift the decimal point to the left by as many digits as there are zeroes in the divisor.

Question 2.

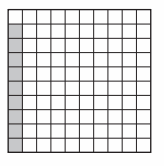
fraction: __________
decimal: __________
Answer:
Total Number of boxes = 100
Number of boxes shaded = 9 .
Fraction = Number of boxes shaded by Total Number of boxes in a grid .
fraction: \(\frac{9}{100}\)
decimal: 0.09
Explanation :
Division by 10, 100 ,1000, etc. Shift the decimal point to the left by as many digits as there are zeroes in the divisor.

Question 3.

fraction: __________
decimal: __________
Answer:
Total Number of boxes = 100
Number of boxes shaded = 65 .
Fraction = Number of boxes shaded by Total Number of boxes in a grid .
fraction: \(\frac{65}{100}\)
decimal: 0.65
Explanation :
Division by 10, 100 ,1000, etc. Shift the decimal point to the left by as many digits as there are zeroes in the divisor.

Question 4.
Color 0.8 of the grid.

Answer:

Explanation :
decimal: 0.8
Multiplying by 100 to numerator and denominator we get fraction as \(\frac{80}{100}\)
Total Number of boxes = 100
Number of boxes shaded = 80 .
Fraction = Number of boxes shaded by Total Number of boxes in a grid .
fraction: \(\frac{80}{100}\)

Question 5.
Color 0.04 of the grid.

Answer:

Explanation :
0.04
Multiplying by 100 to numerator and denominator we get fraction as \(\frac{80}{100}\)
Total Number of boxes = 100
Number of boxes shaded = 4 .
Fraction = Number of boxes shaded by Total Number of boxes in a grid .
fraction: \(\frac{4}{100}\)

Question 6.
Color 0.53 of the grid.

Answer:

Explanation :
decimal: 0.53
Multiplying by 100 to numerator and denominator we get fraction as \(\frac{80}{100}\)
Total Number of boxes = 100
Number of boxes shaded = 53 .
Fraction = Number of boxes shaded by Total Number of boxes in a grid .
fraction: \(\frac{53}{100}\)

Practice

Question 7.
The numbers 81, 27, and 45 are all multiples of 1, ___, and ___.
Answer:
The numbers 81, 27, and 45 are all multiples of 1, 3, and 9 .

Question 8.
List the first ten multiples of 6.
___, ___, ___, ___, ___, ___, ___, ___, ___, ___.
Answer :
The first ten multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 , 66 .

Everyday Math Grade 4 Home Link 3.10 Answer Key

Tenths and Hundredths

Family Note Your child continues to work with decimals. Encourage him or her to think about ways to write money amounts. This is called dollars-and-cents notation. For example, $0.07 (7 cents), $0.09 (9 cents), and so on.

Write the decimal numbers that represent the shaded part in each diagram .

Question 1.

__ hundredths
__ tenths __ hundredths
Answer:
Total Number of boxes = 100
Number of boxes shaded = 57 .
Fraction = Number of boxes shaded by Total Number of boxes in a grid .
fraction: \(\frac{57}{100}\)
decimal = 0.53 .
5 tenths 7 hundredths.
57 hundredths
Explanation :
To the right of the decimal point are the tenths and hundredths, where you put digits that represent numbers that are fractional parts of one, numbers that are more than zero and less than one

Question 2.

__ hundredths
__ tenths __ hundredths
Answer:
Total Number of boxes = 100
Number of boxes shaded = 70 .
Fraction = Number of boxes shaded by Total Number of boxes in a grid .
fraction: \(\frac{70}{100}\)
decimal = 0.70 .
7 tenths 0 hundredths.
0 hundredths
Explanation :
To the right of the decimal point are the tenths and hundredths, where you put digits that represent numbers that are fractional parts of one, numbers that are more than zero and less than one

Question 3.

__ hundredths
__ tenths __ hundredths
Answer:
Total Number of boxes = 100
Number of boxes shaded = 4 .
Fraction = Number of boxes shaded by Total Number of boxes in a grid .
fraction: \(\frac{4}{100}\)
decimal = 0.04 .
0 tenths 4 hundredths.
4 hundredths .
Explanation :
To the right of the decimal point are the tenths and hundredths, where you put digits that represent numbers that are fractional parts of one, numbers that are more than zero and less than one

Write the words as decimal numbers.

Question 4.
twenty-three hundredths ___
Answer:
twenty-three hundredths = 0.23
Explanation :
23 hundredths would be written as . 23 as a decimal. 23 hundredths is the same as the fraction 23/100, or 23 out of 100 parts.

Question 5.
eight and four-tenths
______
Answer:
eight and four-tenths = 8.4

Question 6.
thirty and twenty-hundredths
____
Answer:
thirty and twenty-hundredths = 30.20

Question 7.
five-hundredths
______
Answer :
five-hundredths = 0.05

Continue each pattern.

Question 8.
0.1, 0.2, 0.3, ____, ___, ___, ___, ____, ___
Answer:
0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9

Question 9.
0.01, 0.02, 0.03, ____, ___, ___, ___, ____, ___
Answer:
0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09

Practice

Question 10.
Round 7,604 to the nearest thousand. ______
Answer:
7,604 to the nearest thousand is 8000 .

Question 11.
Round 46,099 to the nearest thousand. ____
Answer:
46,099 to the nearest thousand is 46,000

Question 12.
Round 8,500,976 three ways: nearest thousand, hundred-thousand, and million.
_____ ____ ____
Answer:
8,500,976 three ways: nearest
thousand = 8,501,000
hundred-thousand = 8,500,000
million = 9,000,000

Everyday Math Grade 4 Home Link 3.11 Answer Key

Practice with Decimals

Fill in the missing numbers.

Question 1.

Answer:

Question 2.

Answer:

Follow these directions on the ruler below.

Question 3.
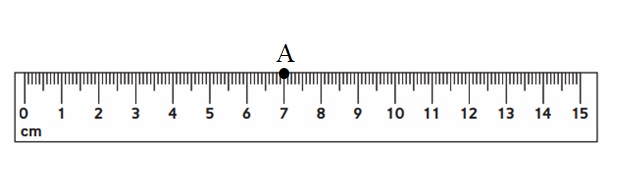
Make a dot at 7 cm and label it with the letter A.
Answer:

Question 4.
Make a dot at 90 mm and label it with the letter B.
Answer:

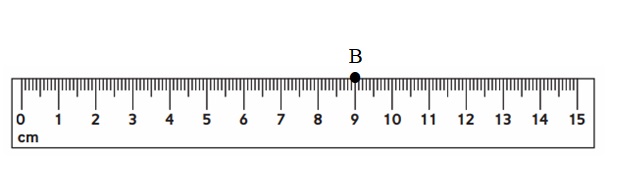
Explanation :
1cm = 10mm
9 cm = 90 mm

Question 5.
Make a dot at 0.13 m and label it with the letter C.
Answer:

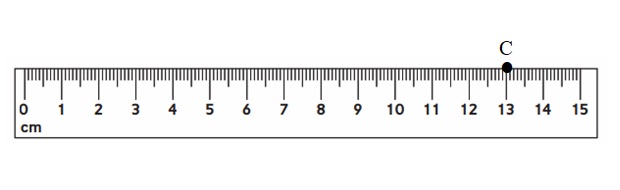
Explanation :
1m = 100 cm
0.13 m = 13 cm

Question 6.
Make a dot at 0.06 m and label it with the letter D.

Answer:

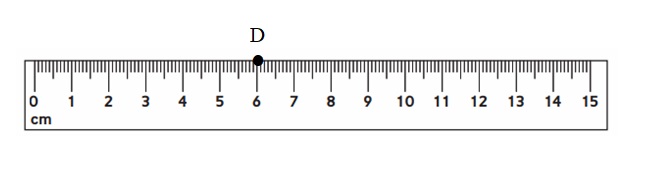
Explanation :
1m = 100 cm
0.06 m = 6 cm

Question 7.
Write <, >, or =.
a. 1.2 ___ 0.12
Answer:
1.2 > 0.12
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

b. 0.3 __ 0.38
Answer:
0.3 < 0.38
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

c. 0.80 __ 0.08
Answer:
0.80 >  0.08
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

Question 8.
Complete.

Answer :

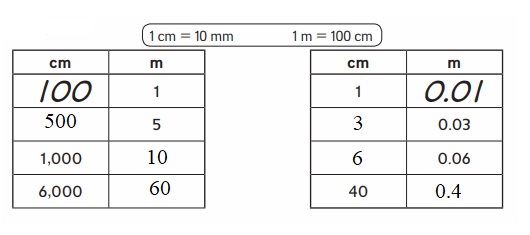
Practice

Question 9.
6,366 + 7,565 = ____
Answer:
6,366 + 7,565 = 13,931

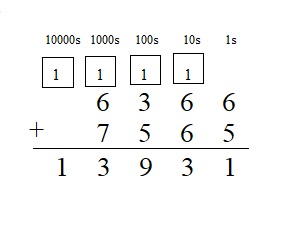
Question 10.
3,238 + 29,784 = ___
Answer:
3,238 + 29,784 = 33022

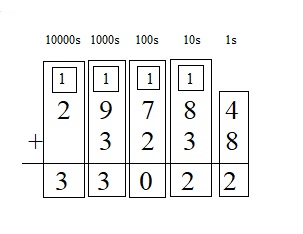
Question 11.
9,325 – 7,756 = ___
Answer:
9,325 – 7,756 = 1569
Explanation :

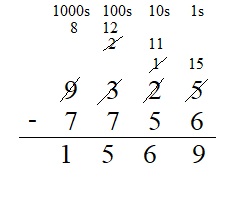
Question 12.
14,805 – 2,927 = ___
Answer:
14,805 – 2,927 = 11878

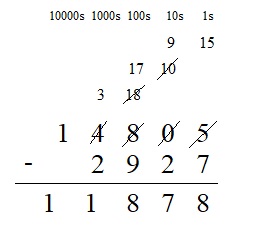
Everyday Math Grade 4 Home Link 3.12 Answer Key

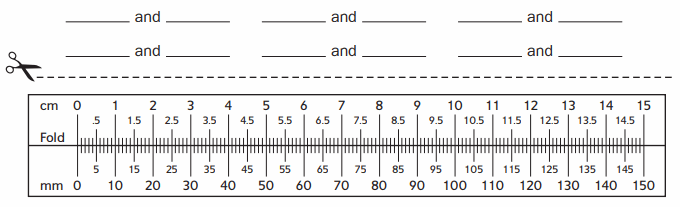
Measuring Centimeters and Millimeters

Question 1.
Find 6 objects in your home to measure. Use the ruler from the bottom of the page to measure them, first in centimeters and then in millimeters. Record your objects and their measurements.

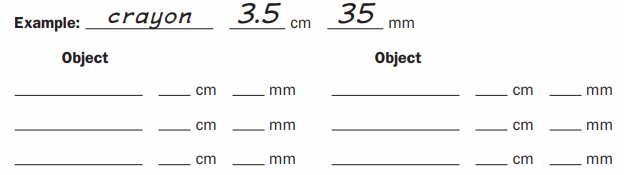
Answer :

Fill in the tables.

Question 2.

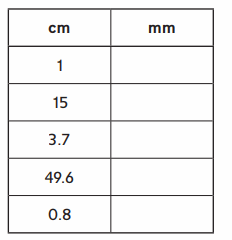
Answer:

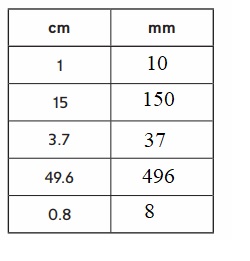
Explanation :
1 cm is 10 mm
multiply the given cm value with 10 to get the value in mm .
Respective given values are converted into mm and written in the above tabular column .

Question 3.

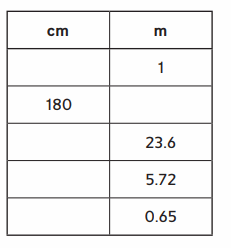
Answer:

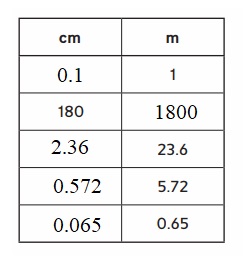
Explanation :
1 cm is 10 mm
multiply the given cm value with 10 to get the value in mm .
divide the given mm value with 10 to get the value in cm .
Respective given values are converted into mm and cm , written in the above tabular column .

Practice

Question 4.
List the factors for 63. ________
Answer:
The factors of 63 are 1, 3, 7, 9, 21 and 63

Question 5.
Write the factor pairs for 60.

Answer:
The factor pairs for 60 are
1 and 60
2 and 30
3 and 20
4 and 15
5 and 12
6 and 10

Everyday Math Grade 4 Home Link 3.13 Answer Key

Comparing Decimals

Family Note Ask your child to read the decimal numerals aloud. Encourage your child to use the following method:

1. Read the whole-number part.
2. Say and for the decimal point.
3. Read the digits after the decimal point as though they form their own number.
4. Say tenths or hundredths, depending on the placement of the right-hand digit. Encourage your child to exaggerate the -ths sound. For example, 2.37 is read as “two and thirty-seven hundredths.”

Write >, <, or =.

Question 1.
2.35 ___ 2.57
Answer:
2.35 < 2.57
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

Question 2.
1.08 __ 1.8
Answer:
1.08 < 1.8
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

Question 3.
0.64 __ 0.46
Answer:
0.64 > 0.46
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

Question 4.
0.90 ___ 0.9
Answer:
0.90 = 0.9
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

Question 5.
42.1 ___ 42.09
Answer:
42.1 > 42.09
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

Question 6.
7.09 __ 7.54
Answer:
7.09 < 7.54
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

Question 7.
0.4 __ 0.40
Answer:
0.4 = 0.40
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

Question 8.
0.26 __ 0.21
Answer:
0.26 > 0.21
Explanation :
when decimals are compared start with tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal.

Question 9.
The 9 in 4.59 stands for 9 ___ or ____.
Answer:
The 9 in 4.59 stands for 9 Hundredths or 0.09 .

Question 10.
The 3 in 3.62 stands for 3 ___ or ___.
Answer :
The 3 in 3.62 stands for 3  Ones or 3 .

Continue each number pattern.

Question 11.
6.56, 6.57, 6.58, ___, ___, ___
Answer:
6.56, 6.57, 6.58, 6.59, 6.60, 6.61
Explanation :
0.01 more

Question 12.
0.73, 0.83, 0.93, __, ___, ___
Answer :
0.73, 0.83, 0.93, 1.03, 1.13, 1.23
Explanation :
0.10 more

Write the number that is 0.1 more.

Question 13.
4.3 ___
Answer:
4.3 + 0.1 = 4.4

Question 14.
4.07 ___
Answer:
4.07 + 0.1 = 4.17

Write the number that is 0.1 less.

Question 15.
8.2 ___
Answer:
8.2 – 0.1 = 8.1

Question 16.
5.63 ___
Answer :
5.63 – 0.1 =5.53

Practice

Question 17.
43,589 + 12,641 = ____
Answer:
43,589 + 12,641 = 56230
Explanation :

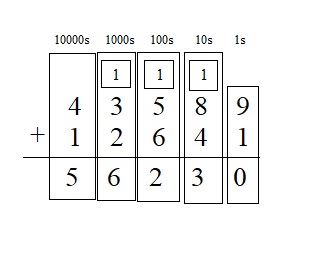
Question 18.
63,274 + 97,047 = ____
Answer:
63,274 + 97,047 = 1,60,321
Explanation :

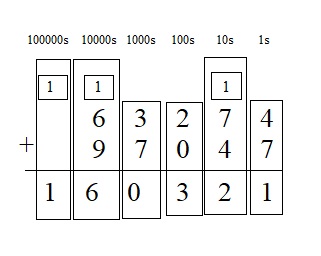
Question 19.
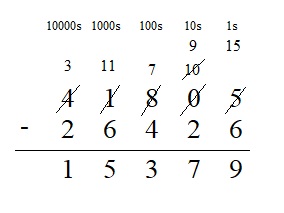
41,805 – 26,426 = ____
Answer:
41,805 – 26,426 = 15379
Explanation :

Question 20.
82,004 – 11,534 = ___
Answer:
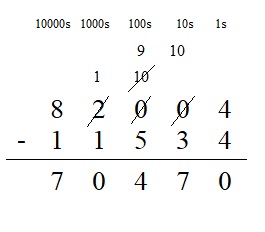
82,004 – 11,534 = 70,470
Explanation :