Everyday Math Grade 4 Answers Unit 1 Place Value; Multidigit Addition and Subtraction

Everyday Mathematics 4th Grade Answer Key Unit 1 Place Value; Multidigit Addition and Subtraction

Everyday Math Grade 4 Home Link 1.2 Answer Key

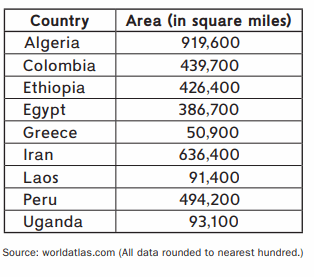
Country Sizes

This table shows the sizes of 10 countries measured in square miles.
Use a place-value tool to help you answer the questions.

Question 1.
Read the numbers to someone at home.
Answer:
The Area of Algeria country = 9,91,600 miles = Nine lakhs ninety one Thousand six hundred .
The Area of Colombia country = 4,39,700 miles = Four lakhs thirty nine thousand and seven hundred .
The Area of Ethiopia country = 4.26,400 miles = Four Lakhs Twenty six thousand and four hundred .
The Area of  Egypt country = 3,86,700 miles = Three Lakhs Eighty six thousand and Seven hundred .
The Area of  Greece country = 50,900 miles = Fifty thousand and Nine hundred .
The Area of Iran country = 6,36,400 miles = Six lakhs thirty six thousand and Four hundred .
The Area of Laos country = 91,400 miles = Ninety one thousand and four hundred .
The Area of Peru country = 4,94,200 miles = Four lakhs Ninety four thousand and two hundred .
The Area of  Uganda country = 93,100 miles = Ninety three thousand and one hundred .

Question 2.
Which is the largest country listed? ___
The smallest? ___
Answer:
The largest country listed is Algeria with Area = 9,91,600 miles = Nine lakhs ninety one Thousand six hundred miles .
The smallest country listed is Greece with Area = 50,900 miles = Fifty thousand and Nine hundred miles .

Question 3.
Compare the areas of Laos and Uganda.
a. Which country has the larger area? ___ How do you know ?
Answer:
The Area of Laos country = 91,400 miles = Ninety one thousand and four hundred .
The Area of  Uganda country = 93,100 miles = Ninety three thousand and one hundred .
93100 > 91400 .
Area of Laos is greater than Area of Uganda .

b. Write a comparison number sentence. ____
Answer:
Compare the areas of Iran and Egypt.
Which country has the larger area? ___ How do you know ?
The Area of Iran country = 6,36,400 miles = Six lakhs thirty six thousand and Four hundred .
The Area of  Egypt country = 3,86,700 miles = Three Lakhs Eighty six thousand and Seven hundred .
6,36,400 miles > 3,86,700 miles
Area of  Iran is greater than Area of Egypt .

Question 4.
Order the countries from largest area to smallest area.

Answer:

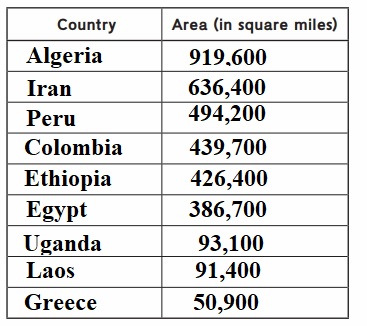
Explanation :
All the country are arranged in descending order that is from larger area to smaller area .

Practice

Question 5.
140 – 60 = ___
Answer:

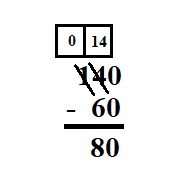
Explanation :
First subtract the ones place values 0 – 0 we get 0
Second subtract the ten place values 4 – 6 so, we cannot subtract 6 from 4 so we regroup take 1 from hundred place that means 10 tens.
so add 10 tens to 4 tens we get 14 tens in hundred place the value becomes 0 . now subtract 14 – 6 we get 8 .

Question 6.
__ = 57 – 39
Answer:

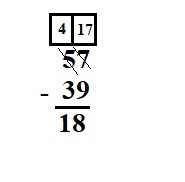
Explanation :
First subtract the ones place values 7 – 9 so, we cannot subtract 9 from 7 so we regroup and take 1 from tens place that means 10 ones.
so add 10 ones to 7 ones we get 17 ones, in tens place the value becomes 4 as we borrowed 1 . 17 – 9 we get 8
Second subtract the ten place values 4 – 3 we get 1 .
Therefore , 57 – 39 = 18 .

Question 7.
115 – 86 = ____
Answer:

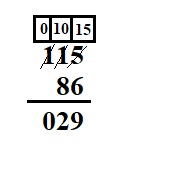
Explanation :
First Subtract ones place values subtract 6 from 5 we cannot subtract 6 from 5 we borrow 1 from tens place that means 10 ones are borrowed added to 5 ones = 15 ones – 6 ones = 9 ones .
then we have 0 ones so borrow 1 from hundred place we get 10 tens then subtract, 10 tens – 8 tens we get 2 tens .
in hundred place we have 0 hundreds .
so, the difference between 115 – 86 = 29 .

Everyday Math Grade 4 Home Link 1.3 Answer Key

Rounding

Question 1.
Round the seating capacities in the table below to the nearest thousand.

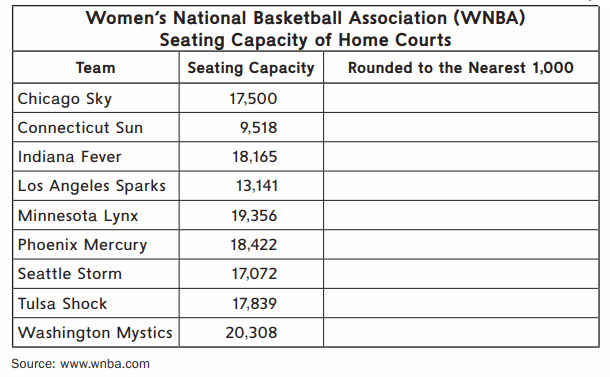
Source: www.wnba.com
Answer:

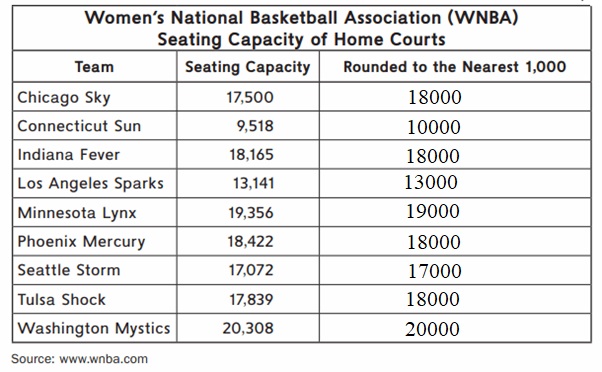
Explanation :
To round a number to the nearest 1000, look at the hundreds digit. If the hundreds digit is 5 or more, round up. If the hundreds digit is 4 or less, round down.

Question 2.
Look at your rounded numbers. Which teams’ arenas have about the same capacity?
Answer:
The Number of Teams which have same capacity 18000 are Chicago sky , Indiana fever , Phoenix Mercury and Tulsa Shock .

Question 3.
Round the population figures in the table below to the nearest hundred-thousand.

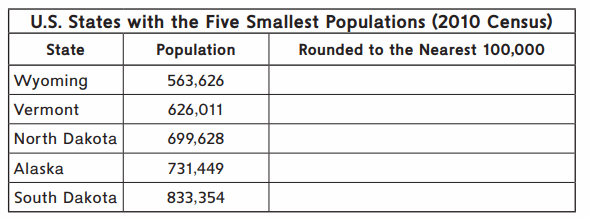
Answer:

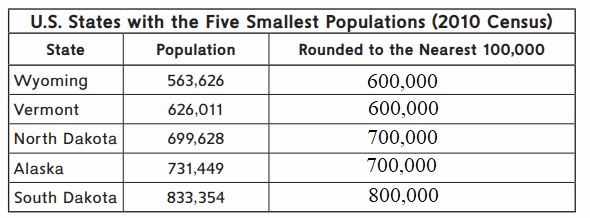
Explanation :
We compare the digit at the ten thousandth place with 5 to round off numbers to the nearest lakh. If the digit in the ten thousandth place is less than five, then we replace the digits in ten thousand, thousand, hundred, tens and ones places with zeros.

Practice

Question 4.
___ = 60 + 60
Answer:

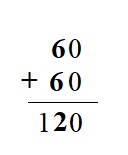
Explanation :
Step 1 : Add the values in the ones place . 0 + 0 = 0. is written in ones place .
Step 2 : Add the values in the tens place 6 + 6 give 12 sum . write 2 in the tens place and carry 1 in the hundreds place .
Step 3 : as there no values in the hundreds place write the carry in the hundred place directly .
Therefore , the sum of 60 and  60 is 120 .

Question 5.
__ = 54 + 59
Answer:

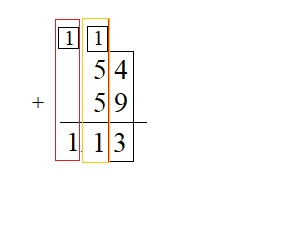
Explanation :
Step 1 : Add the values in the ones place . 4 + 9 = 13 . Write 3 in the ones place and carry forward 1 to the tens place .
Step 2 : Add the values in the tens place 5 + 5 + 1 as 1 is a carry forward give 11 sum . write 1 in the tens place and carry 1 in the hundreds place .
Step 3 : as there no values in the hundreds place write the carry in the hundred place directly .
Therefore the sum of 54 and 59 is 113 .

Question 6.
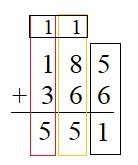
185 + 366 = __
Answer:

Explanation :
Step 1 : Add the values in the ones place . 5 + 6 = 11 . Write 1 in the ones place and carry forward 1 to the tens place .
Step 2 : Add the values in the tens place 8 + 6 + 1 as 1 is a carry forward give sum 15 . write 5 in the tens place and carry 1 in the hundreds place .
Step 3 : Add the values in the hundred place 1+ 3 + 1 = 5 , as 1 is the carry forward .
Therefore the sum of 185 and 366 is 551 .

Everyday Math Grade 4 Home Link 1.4 Answer Key

Professional Sports Attendance

The table below shows the attendance for various 2013–2014 professional sports teams. Use the table and a place-value tool to answer the questions.

Source: ESPN NHL Attendance report 2013–2014 and ESPN MLB Attendance report 2012
* Baseball attendance is for the Chicago Cubs and the New York Yankees.
* Hockey attendance is for the New York Rangers.

Question 1.
Which sport had the greater attendance? ____
Answer:
The Attendance of Base ball is greater than Hockey
Explanation :
The attendance of Base ball of different locations is in hundred thousands where as the attendance of hockey of different locations is in ten thousands . so base ball attendance is greater than hockey attendance .

Question 2.
Round the attendance at the hockey games

Answer:

Explanation :
The numbers we write here are 0, 100,000, 200,000, 300,000 and so on.  Check the ten thousand place if the number is 5 or greater then round up . if the ten thousand value is below 5 then we replace the digits in ten thousand, thousand, hundred, tens and ones places with zeros.

The rule for rounding to the nearest ten thousand is to look at the last four digits. If the last four digits are 5,000 or greater, then we round our ten thousands digit up, and if it is less than 5,000, then we keep our ten thousands digit the same and then we replace the digits in thousand, hundred, tens and ones places with zeros.

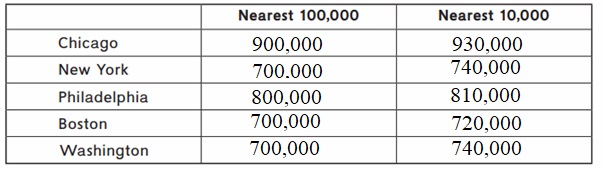
Question 3.
Round the attendance for each baseball team to the nearest million.
Chicago: ____ New York: ____
Philadelphia: ___ Boston: _____
Washington: ____
Answer:
the attendance for each baseball team to the nearest million 10,00,000
Chicago: 3,000,000
New York: 4,000,000
Philadelphia: 4,000,000
Boston: 3,000,000
Washington: 2,000,000
Explanation :If the digit in the hundred thousand’s place in a number is 0, 1, 2, 3 or 4 then round to the nearest multiple of one million which is smaller than the given number.
If the digit in the hundred thousand’s place in a number is 5, 6, 7, 8 or 9 then round to the nearest multiple of one million which is greater than the given number.
Thus, to round off numbers to the nearest one million, look at the digit in the hundred thousand place.

Question 4.
List the cities in order from greatest to least hockey attendance.
Answer:
The Attendance of cities from greatest to least hockey attendance are
Chicago > Philadelphia > Washington > New York > Boston .

Question 5.
Write a number sentence comparing the greatest and least baseball attendances. Use <, >, or =.
Answer:
Which city has more attendance in baseball game New York or Philadelphia ?
Attendance of baseball in New York = 3,542,406
Attendance of baseball in Philadelphia = 3,565,718
3,565,718 > 3,542,406
Attendance of baseball in Philadelphia  > Attendance of baseball in New York
Explanation :
(a) If two numbers have the same number of digits, we compare them on the basis of their extreme left digits. The number with the greater extreme left digit is greater.
(b) If the extreme left digits of two numbers are the same, we compare them on the basis of the next digits towards their right and so on.
Both numbers have same numbers of digits.
Let us compare the digits in the left most place, we find the both numbers have same digits in million and hundred thousands place. Next, we compare the digits at ten-thousands place. Here 6 > 4.
Therefore, 3,565,718 > 3,542,406 .

Practice

Question 6.
210 – 150 = ___
Answer:

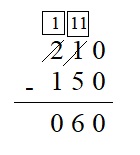
Explanation :
Step 1 : First subtract the ones place values 0 – 0 we get, 0
Step 2 : Subtract tens place values subtract 5 from 1 we cannot 5 from 1 so 1 hundred is borrowed from hundred place value  so 2 is reduced to 1 and 1 hundred is equal 10 tens so add 10 tens to 1 tens so, we have 11 tens – 5 tens gives 6 tens . 6 is written in the tens place .
Step 3 : 1 hundred is borrowed from 2 so 2 is reduced to 1 hundred 1 – 1 gives 0 . o is written in hundred place .
Therefore , 210 – 150 = 60 .

Question 7.
140 – 80 = ___
Answer:

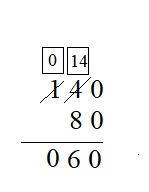
Explanation :
Step 1 : First subtract the ones place values 0 – 0 we get, 0
Step 2 : Subtract tens place values subtract 8 from 4 we cannot subtract 8 from 4 so 1 hundred is borrowed from hundred place value  so 1 is reduced to 0 and 1 hundred is equal 10 tens so add 10 tens to 4 tens so, we have 14 tens – 8 tens gives 6 tens . 6 is written in the tens place .
Step 3 : 1 hundred is borrowed from 1 so 1 is reduced to 0 hundred, 0 is written in hundred place .
Therefore , 140 – 80 = 60 .

Question 8.
93 – 58 = ___
Answer :

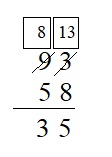
Explanation :
Step 1 : Subtract ones place values subtract 8 from 3 we cannot subtract 8 from 4 so 1 tens is borrowed from tens place value  so 9 is reduced to 8 tens and 1 tens is equal 10 ones so add 10 ones to 3 ones so, we have 13 ones – 8 tens gives 5 tens . 5 is written in the ones place .
Step 2 : 1 tens is borrowed from 9 so 9 is reduced to 8 tens, 8 – 5 is 3 tens, 3 is written in tens place .
Therefore , 93 – 58 = 35 .

Everyday Math Grade 6 Home Link 1.5 Answer Key

Using Estimation Strategies

Family Note Today students explored different ways of estimating: rounding (in which all numbers are rounded to a particular place value), front-end estimation (all digits to the right of the greatest place value become zeros), and using close-but-easier numbers (numbers are rounded to a number that is close in value and easy to work with). While all methods of estimation are equally valid, some may be more helpful than others for answering specific kinds of questions.

Read the number stories. Choose an appropriate estimation strategy.

Question 1.
On the walk home from school, Meg stopped at the library for 22 minutes and at her grandmother’s house for 38 minutes. She spent 17 minutes walking. She left at 3:00 and was supposed to be home by 4:00.
a. Did Meg make it home on time? How did you get your answer?
Answer:
Estimation :
No, Meg Did not reach in Time .
I rounded the times to tens place and added
22 –> 20
38 –> 40
17 –> 20
then added we get , 80 minutes that is 1 hour 20 minutes .
Explanation :
Time spent at Library by Meg = 22 minutes
Time spent at grandmother’s house by Meg = 38 minutes
Time spent in Walking = 17 minutes
Total time spent by Meg from home to school = 22 + 38 + 17 = 77 minutes = 1 hour 17 minutes.
The Time Meg started to home = 3 : 00
The Time Meg reached home = 3: 00 + 1:17 mins = 4 : 17 mins
The Time she supposed to be home is 4 :00
That means Meg did not reach home on time .
Therefore she is 17 mins late to reach Home .

b. Why did you choose your estimation strategy?
Answer:
All Numbers are closer to multiple of tens so , i just need to check that they are added up to less or more than 60 minutes .

Question 2.
You and two friends need to make 100 tacos for a party. You have made 31 tacos. Your friend Chris has made 24 tacos. Your friend Pat thinks he needs to make at least 60 tacos to have enough for the party.
a. Is Pat correct? __ How did you get your answer?
Answer:
No,
Explanation :
I used close- but -easier numbers
Number of Tacos needed for party = 100
Number of Tacos made by me = 31 –> rounded to –> 30
Number of tacos made by Chris = 24 –> rounded to –> 25
Total Tacos made by me and Chris = 30 + 25 = 55
Number of Tacos should be made by Pat = 100 – 55 = 45

b. Why did you choose your estimation strategy?
Answer:
I have chosen close- but -easier numbers because all the number given are friendly numbers easy in solving .

Practice

Question 3.
31 + 51 = ___
Answer:

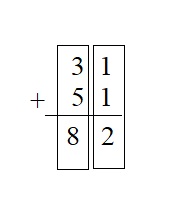
Explanation :
Step 1 : Add the values in the ones place . 1 + 1 = 2 . Write 2 in the ones place
Step 2 : Add the values in the tens place 3 + 5 = give sum 8 . write 8 in the tens place
Therefore the sum of 31 and 51 is 82 .

Question 4.
45 + 64 = ___
Answer:

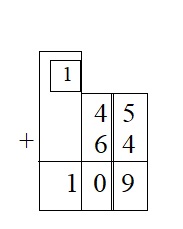
Explanation :
Step 1 : Add the values in the ones place . 5 + 4 = 9 . Write 9 in the ones place
Step 2 : Add the values in the tens place 4 + 6  gives sum 10 . write 0 in the tens place and carry 1 in the hundreds place .
Step 3 : Add the values in the hundred place as there are no values in hundred directly write the carry forward value 1 in the hundred place
Therefore the sum of 45 and 64 is 109 .

Question 5.
252 + 144 = ___
Answer:

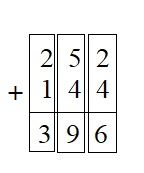
Explanation :
Step 1 : Add the values in the ones place . 2 + 4 = 6 . Write 6 in the ones place .
Step 2 : Add the values in the tens place 5 + 4 gives sum 9 . write 9 in the tens place .
Step 3 : Add the values in the hundred place 2+ 1= 3
Therefore the sum of 252 and 144 is 396 .

Everyday Math Grade 4 Home Link 1.6 Answer Key

Animal Number Stories

Estimate. Then solve each number story.

Question 1.
The zoo needs to move four animals in a truck that can carry only 700 pounds. A leopard can weigh up to 176 pounds. A warthog can weigh up to 250 pounds. A chimpanzee can weigh as much as 130 pounds. What is the maximum weight
that the fourth animal can be?
Estimate: About __ pounds
Answer: ___ pounds
Number model with answer: _______
Does your answer make sense? ___ How do you know?
Answer:
Estimate :
Weight of the Truck can carry = 700 pounds
Weight of the leopard = 176 pounds ==> 180
Weight of the Warthog = 250 pounds ==> 250
Weight of the Chimpanzee = 130 pounds . ==> 130
Maximum weight of the Fourth Animal can be = 700 – ( 180 + 250 + 130 ) = 700 – 560 = 140 pounds .
Answer :
Weight of the Truck can carry = 700 pounds
Weight of the leopard = 176 pounds
Weight of the Warthog = 250 pounds
Weight of the Chimpanzee = 130 pounds .
Maximum weight of the Fourth Animal can be = 700 – ( 176 + 250 + 130 ) = 700 – 556 = 144 pounds .
Yes , My Estimate was 140 pounds which is near to the answer 144 pounds.

Question 2.
The combined weight of a mountain lion, an orangutan, and a wolf can be as much as 491 pounds. If the wolf weighs 175 pounds and the orangutan weighs 180 pounds, how much do two mountain lions weigh?
Estimate: About ___ pounds
Answer: ___ pounds
Number model with answer: ____
Does your answer make sense? ___ How do you know?

Source: maximum animal weights from www.nationalgeographic.com
Estimate :
Total Weight of all Animals = 491 pounds ==> 490 pounds
Weight of Wolf = 175 pounds  ==> 175 pounds
Weight of Orangutan = 180 pounds  ==> 180 pounds
Weight of Mountain Lion =  total  – ( wolf + Orangutan ) weight  = 490 – ( 175 + 180 ) = 490 – 355 = 135
Weight of Two Mountain lions = 2 ( 135 ) = 270 pounds
Answer :
Total Weight of all Animals = 491 pounds
Weight of Wolf = 175 pounds
Weight of Orangutan = 180 pounds
Weight of Two Mountain Lions =  total  – ( wolf + Orangutan ) weight  = 491 – ( 175 + 180 ) = 491 – 355 = 136 pounds
Weight of Two Mountain lions = 2 ( 136 ) = 272 pounds
Yes , My Estimate was 270 pounds which is near to the answer 272 pounds

Practice

Question 3.
5 + 8 = ___
Answer:
5 + 8 = 13

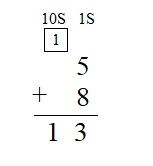
Explanation :
Step 1 : Add the values in the ones place . 5 + 8 = 13 . 3 is written in ones place  and 1 is carry forwarded to tens place .
Step 2 : as there no values in the tens place write the carry in the tens place directly .
Therefore , the sum of 5 and 8 is 13 .

Question 4.
9 + 6 = ___
Answer:

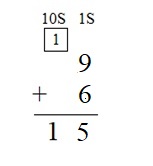
Explanation :
Step 1 : Add the values in the ones place . 9 + 6 = 15 . 5 is written in ones place  and 1 is carry forwarded to tens place .
Step 2 : as there no values in the tens place write the carry in the tens place directly .
Therefore , the sum of 9 and 6 is 15 .

Question 5.
70 + 50 = ___
Answer:

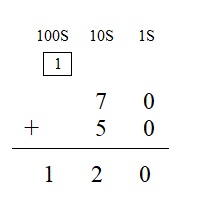
Explanation :
Step 1 : As there are no values in ones then write directly 0 in the ones place .
Step 2 : Add the values in the tens place 7 + 5  gives sum 12 . write 2 in the tens place and carry 1 to the hundreds place .
Step 3 : Add the values in the hundred place as there are no values in hundred place directly write the carry forward value 1 in the hundred place
Therefore the sum of 70 and 50 is 120 .

Question 6.
___ = 80 + 50
Answer:

Explanation :
Step 1 : As there are no values in ones then write directly 0 in the ones place .
Step 2 : Add the values in the tens place 8 + 5  gives sum 13 . write 3 in the tens place and carry 1 to the hundreds place .
Step 3 : Add the values in the hundred place as there are no values in hundred place directly write the carry forward value 1 in the hundred place
Therefore the sum of 80 and 50 is 130 .

Question 7.
67 + 94 = ___
Answer:

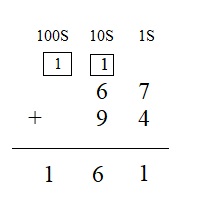
Explanation :
Step 1 : Add the values in the ones place . 7 + 4 = 11 . 1 is written in ones place  and 1 is carry forwarded to tens place .
Step 2 : Add the values in the tens place 6 + 9 + 1 gives sum 16, even carry forward is added . write 6 in the tens place and carry 1 to the hundreds place
Step 3 : Add the values in the hundred place as there are no values in hundred place directly write the carry forward value 1 in the hundred place
Therefore the sum of 67 and 94 is 161 .

Question 8.
___ = 425 + 275
Answer:

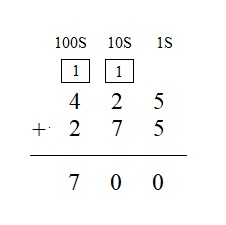
Explanation :
Step 1 : Add the values in the ones place . 5 + 5 = 10 . 0 is written in ones place  and 1 is carry forwarded to tens place .
Step 2 : Add the values in the tens place 2 + 7 + 1 gives sum 10, even carry forward is added . write 0 in the tens place and carry 1 to the hundreds place
Step 3 : Add the values in the hundred place 4 + 2+ 1 gives sum 7, even carry forward is added . 7 is written in the hundred place
Therefore the sum of 425 and 275 is 700 .

Everyday Math Grade 4 Home Link 1.7 Answer Key

U.S. Traditional Addition

Family Note In today’s lesson students were introduced to U.S. traditional addition. The steps are listed below

Step 1

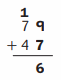
Add the 1s: 9 + 7 = 16.
16 ones = 1 ten and 6 ones + 4 7
Write 6 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2

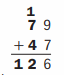
Add the 10s: 7 + 4 + 1 = 12. 7 9
12 tens = 1 hundred + 2 tens
Write 2 in the 10s place below the line.
Write 1 in the 100s place below the line.

Make an estimate. Write a number model to show what you did. Then solve using U.S. traditional addition. Compare your answer with your estimate to see if your answer makes sense.

Question 1.

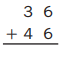
Estimate: ______
Answer:

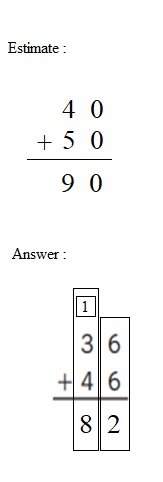
Step 1
Add the 1s: 6 + 6 = 12.
12 ones = 1 ten and 2 ones + 4 6
Write 2 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 3 + 4 + 1 = 8.
Write 8 in the 10s place below the line.

Question 2.

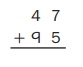
Estimate: ______
Answer:

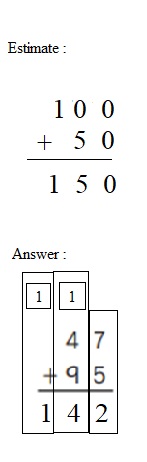
Explanation :
Step 1
Add the 1s: 7 + 5 = 12.
12 ones = 1 ten and 2 ones + 9 5
Write 2 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 4 + 9 + 1 = 14
14 tens = 1 hundred + 4 tens
Write 4 in the 10s place below the line.
Write 1 above the digits in the 100s place.
No values to add in the hundred so write 1 below the line in 100s place .

Question 3.
784 + 889 =
Estimate: ______
Answer:

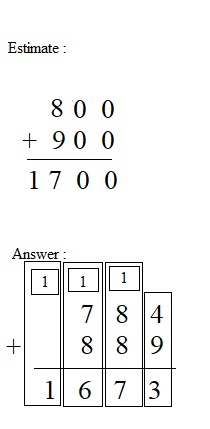
Explanation :
Step 1
Add the 1s: 4 + 9 = 13.
13 ones = 1 ten and 3 ones
Write 3 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 8 + 8 + 1 = 17
17 tens = 1 hundred + 7 tens
Write 7 in the 10s place below the line.
Write 1 above the digits in the 100s place.

Step 3
Add the 100s: 7 + 8 + 1 = 16
16 hundreds = 1 thousand + 6 hundred
Write 6 in the 100s place below the line.
Write 1 above the digits in the 1000s place.
No values to add in the thousand’s place so write 1 below the line in 1000s place .

Question 4.

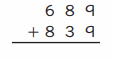
Estimate: ______
Answer:

Step 1
Add the 1s: 9 + 9 = 18.
18 ones = 1 ten and 8 ones
Write 8 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 8 + 3 + 1 = 12
12 tens = 1 hundred + 2 tens
Write 2 in the 10s place below the line.
Write 1 above the digits in the 100s place.

Step 3
Add the 100s: 6 + 8 + 1 = 15
15 hundreds = 1 thousand + 5 hundred
Write 5 in the 100s place below the line.
Write 1 above the digits in the 1000s place.
No values to add in the thousand’s place so write 1 below the line in 1000s place .

Question 5.
279 + 1,795 = ___
Estimate: ______
Answer:

Step 1
Add the 1s: 9 + 5 = 14.
14 ones = 1 ten and 4 ones
Write 4 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 7 + 9 + 1 = 17
17 tens = 1 hundred + 7 tens
Write 7 in the 10s place below the line.
Write 1 above the digits in the 100s place.

Step 3
Add the 100s: 2 + 7 + 1 = 10
10 hundreds = 1 thousand + 0 hundred
Write 0 in the 100s place below the line.
Write 1 above the digits in the 1000s place.

Step 4
Add the 1000s:  1 + 1 = 2
Write 2 in the 1000s place below the line.

Question 6.
3,746 + 6,255 = ___
Estimate: ______
Answer:

Step 1
Add the 1s: 6 + 5 = 11.
11 ones = 1 ten and 1 ones
Write 1 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 4 + 5 + 1 = 10
10 tens = 1 hundred + 0 tens
Write 0 in the 10s place below the line.
Write 1 above the digits in the 100s place.

Step 3
Add the 100s: 7 + 2 + 1 = 10
10 hundreds = 1 thousand + 0 hundred
Write 0 in the 100s place below the line.
Write 1 above the digits in the 1000s place.

Step 4
Add the 1000s: 3 + 6 + 1 = 10
10 thousands = 1 ten thousands + 0 thousands
Write 0 in the 1000s place below the line.
Write 1 above the digits in the 10000s place.
No values to add in the ten thousand’s place so write 1 below the line in 10000s place .

Practice

Question 7.
Round 2,787 to the nearest . . .
hundred ____ thousand ___
Answer:
2787
hundred = 2790
thousand = 2800
Explanation :
Rules for Rounding off to the Nearest 100:
Rule I: While rounding off to the nearest hundred, if the digit in the tens place is between 0 – 4 i.e. < 5, then the tens place is replaced by ‘0’.
Rule II: If the digit in the units place is equal to or >5, then the tens place is replaced by ‘0’ and the hundreds place is increased by 1.

Rules for Rounding off to the Nearest 1000:
Rule I: While rounding off to the nearest thousand, if the digit in the hundreds place is between 0 – 4 i.e., < 5, then the hundreds place is replaced by ‘0’.
Rule II: If the digit in the hundreds place is = to or > 5, then the hundreds place is replaced by ‘0’ and the thousands place is increased by 1.

Question 8.
Round 54,681 to the nearest . . .
thousand ___ ten-thousand ___
Answer:
54,681
thousand = 54,700
ten-thousand = 54,000
Explanation :
Rules for Rounding off to the Nearest 1000:
Rule I: While rounding off to the nearest thousand, if the digit in the hundreds place is between 0 – 4 i.e., < 5, then the hundreds place is replaced by ‘0’.
Rule II: If the digit in the hundreds place is = to or > 5, then the hundreds place is replaced by ‘0’ and the thousands place is increased by 1.

Rounding off to the nearest ten thousand (10,000):
If the digit in the thousand’s place in a number is 0, 1, 2, 3 or 4 then round to the nearest multiple of ten thousand which is smaller than the given number.
If the digit in the thousand’s place in a number is 5, 6, 7, 8 or 9 then round to the nearest multiple of ten thousand which is greater than the given number.
Thus, to round off numbers to the nearest ten thousand look at the digit in the one thousands place.

 

Everyday Math Grade 4 Home Link 1.8 Answer Key

Grouping by Multiples of 10

Alfie is ordering table tennis balls for the recreation center. A box holds 10 balls. A carton of table tennis balls holds 10 boxes.

Question 1.
How many table tennis balls are in one carton?
Answer:
Number of balls in one box = 10 balls .
Number of boxes in 1 carton = 10 boxes .
Total Number of Balls in one carton = (number of balls )  × ( number of boxes ) = 10  × 10 = 100 balls  .
Therefore, Total Number of  Balls in one carton = 100 balls .

Question 2.
Alfie ordered 7 cartons and 3 boxes of table tennis balls. How many balls did he order? ___
Show how you know your answer is correct.
Answer:
Number of balls in one box = 10 balls .
Number of boxes in 1 carton = 10 boxes .
Total Number of Balls in one carton = (number of balls )  × ( number of boxes ) = 10  × 10 = 100 balls  .
Number of Balls in 7 carton  = 7  × 100 = 700 balls  .
Number of balls in 3 boxes = 3  × 10 = 30 balls  .
Total Number of balls in 7 carton and 3 boxes = 700 + 30  = 730 balls .

Question 3.
Explain how the cartons and boxes for table tennis balls are like the digits for numbers in our base-10 number system.
Answer:
The Number of balls in the cartons represents the digit in 100 place and  The Number of balls in the boxes represents the digit in 10 place .

Practice

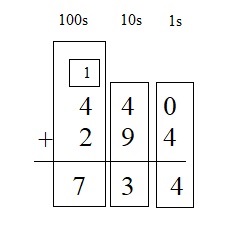
Question 4.
440 + 294 = ___
Answer:

Explanation :
Step 1
Add the 1s: 0 + 4 = 4.
Write 4 in the 1s place below the line.

Step 2
Add the 10s: 4 + 9 = 13
13 tens = 1 hundred + 3 tens
Write 3 in the 10s place below the line.
Write 1 above the digits in the 100s place.

Step 3
Add the 100s: 4 + 2 + 1 = 7
Write 7 in the 100s place below the line.
Therefore, sum of 440 and 294 = 734 .

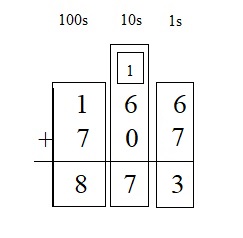
Question 5.
166 + 707 = ___
Answer:

Explanation :

Step 1
Add the 1s: 6 + 7 = 13.
13 ones = 1 ten and 3 ones
Write 3 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 6 + 0 + 1 = 7
Write 7 in the 10s place below the line.

Step 3
Add the 100s: 1 + 7 = 8
Write 8 in the 100s place below the line.
Therefore sum of 166 and 707 = 873 .

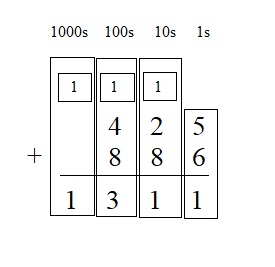
Question 6.
___ = 425 + 886
Answer:

Step 1
Add the 1s: 5 + 6 = 11.
11 ones = 1 ten and 1 ones
Write 1 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 2 + 8 + 1 = 11
11 tens = 1 hundred + 1 tens
Write 1 in the 10s place below the line.
Write 1 above the digits in the 100s place.

Step 3
Add the 100s: 4 + 8 + 1 = 13
13 hundreds = 1 thousand + 3 hundred
Write 3 in the 100s place below the line.
Write 1 above the digits in the 1000s place.
No values to add in the thousand’s place so write 1 below the line in 1000s place .

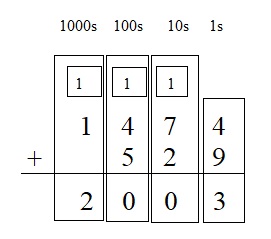
Question 7.
1,474 + 529 = ___
Answer:

Step 1
Add the 1s: 4 + 9 = 13.
13 ones = 1 ten and 3 ones
Write 3 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 7 + 2 + 1 = 10
10 tens = 1 hundred + 0 tens
Write 0 in the 10s place below the line.
Write 1 above the digits in the 100s place.

Step 3
Add the 100s: 4 + 5 + 1 = 10
10 hundreds = 1 thousand + 0 hundred
Write 0 in the 100s place below the line.
Write 1 above the digits in the 1000s place.
No values to add in the thousand’s place so write 1 below the line in 1000s place .

Everyday Math Grade 4 Home Link 1.9 Answer Key

U.S. Traditional Subtraction

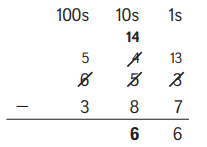
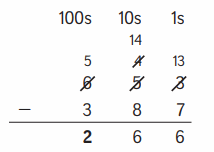
Family Note In today’s lesson students were introduced to U.S. traditional subtraction. The process is shown below for the problem 653 – 387.
Step 1:
Start with the ones. Trade 1 ten for 10 ones. Subtract the ones.

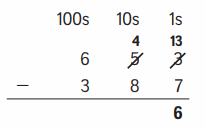
Step 2:
Go to the tens. Trade 1 hundred for 10 tens. Subtract the tens.

Step 3:
Go to the hundreds. We don’t need to regroup, so just subtract.

Make an estimate. Write a number model to show what you did. Then solve using U.S. traditional subtraction. Compare your answer with your estimate to see whether your answer makes sense.

Question 1.

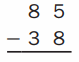
Estimate: _______
Answer:

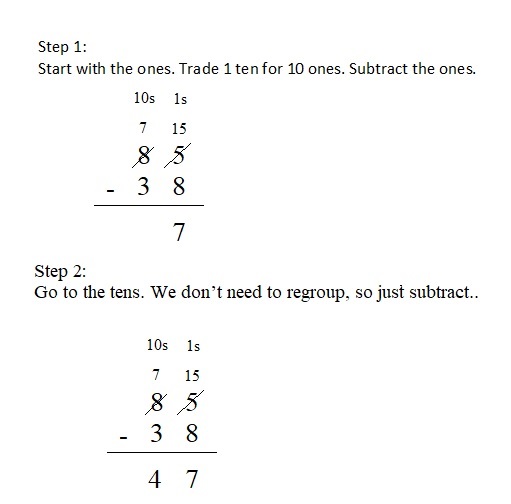
Estimate :
85 ==> 85
38 ==> 40
85 – 40 = 45
Step 1 :
Subtract ones 5 – 0 we get 5 write 5 in the ones places
subtract tens 8 – 4 = 4 write 4 in the tens place .
Therefore difference of 85 and 40 is 45 . which is close to the 47 .

Question 2.

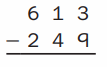
Estimate: _______
Answer:

Estimate :
613 ==> 650
249 ==> 250
650 – 250 = 400
Step 1 :
Subtract ones 0 – 0 we get 0 write 0 in the ones place
subtract tens 5 – 5 = 0 write 0 in the tens place .
subtract hundred 6 – 2 = 4 write 4 in the hundred place .
Therefore difference of 650 and 250 is 400 . which is close to the 364.

Question 3.
506 – 187 = ___
Estimate: _______
Answer:

Estimate :
506 ==> 510
187 ==> 200
500 – 200 = 310
Step 1 :
Subtract ones 0 – 0 we get 0 write 0 in the ones place
subtract tens 1 – 0 = 0 write 1 in the tens place .
subtract hundred 5 – 2 = 3 write 4 in the hundred place .
Therefore difference of 510 and 200 is 310 . which is close to the 319.

Question 4.
951 – 695 = ___
Estimate: _______
Answer:

Estimate :
915 ==> 920
695 ==> 700
920 – 700 = 220
Step 1 :
Subtract ones 0 – 0 we get 0 write 0 in the ones place
subtract tens 2 – 0 = 0 write 2 in the tens place .
subtract hundred 9 – 7 = 2 write 2 in the hundred place .
Therefore difference of 920 and 700 is 220 . which is close to the 256

Question 5.

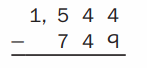
Estimate: _______
Answer:

Estimate :
1544 ==> 1550
749 ==> 750
1550 – 750 = 800
Step 1 :
Subtract ones 0 – 0 we get 0 write 0 in the ones place
subtract tens 5 – 5 = 0 write 0 in the tens place .
subtract hundred 5 – 7 we cannot subtract 7 from 5 we trade 1 from thousands for 10 hundreds we get 10 + 5 = 15 hundreds now subtract 15 – 7 = 8 hundreds  write 8 in the hundred place . subtract thousands 7 – 5 = 2 write 2 in the thousand place .
Therefore difference of 1550 and 750 is 800 . which is close to the 795 .

Question 6.
7,003 – 4,885 =
Estimate: _______
Answer:

Estimate :
7003 ==> 7000
4885 ==> 5000
7000 – 5000 = 2000
Step 1 :
Subtract ones 0 – 0 we get 0 write 0 in the ones place
subtract tens 0 – 0 = 0 write 0 in the tens place .
subtract hundred 0 – 0 = 0 write 0 in the hundred place .
subtract thousands 7 – 5 = 2 write 2 in the thousand place .
Therefore difference of 7000 and 5000 is 2000 . which is close to the 2118

Practice

Question 7.
740 + 294 = ____
Answer:

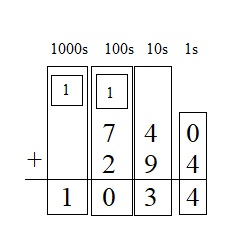
Explanation :

Step 1
Add the 1s: 0 + 4 = 4.
Write 1 in the 1s place below the line.

Step 2
Add the 10s: 4 + 9 = 13
13 tens = 1 hundred + 3 tens
Write 3 in the 10s place below the line.
Write 1 above the digits in the 100s place.

Step 3
Add the 100s: 7 + 2 + 1 = 10
10 hundreds = 1 thousand + 0 hundred
Write 0 in the 100s place below the line.
Write 1 above the digits in the 1000s place.
No values to add in the thousand’s place so write 1 below the line in 1000s place .

Question 8.
2,566 + 807 = ___
Answer:

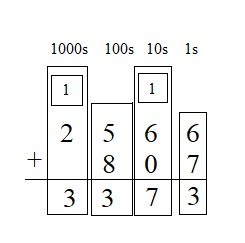
Explanation :

Step 1
Add the 1s: 6 + 7 = 13.
13 ones = 1 ten and 3 ones
Write 3 in the 1s place below the line.
Write 1 above the digits in the 10s place.

Step 2
Add the 10s: 6 + 0 + 1 = 7
Write 7 in the 10s place below the line.

Step 3
Add the 100s: 5 + 8 = 13
13 hundreds = 1 thousand + 3 hundred
Write 3 in the 100s place below the line.
Write 1 above the digits in the 1000s place.

Step 4
Add the 1000s: 2 + 1 = 3
Write 3 in the 1000s place below the line.

Everyday Math Grade 4 Home Link 1.10 Answer Key

Snake Lengths

Use the measurement scales to solve the problems.

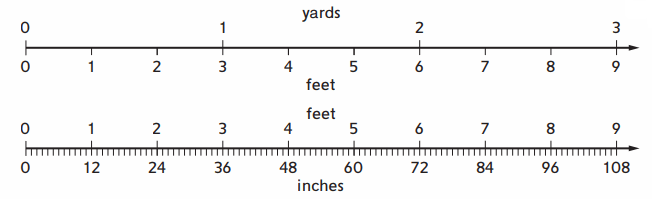
Question 1.

Answer:

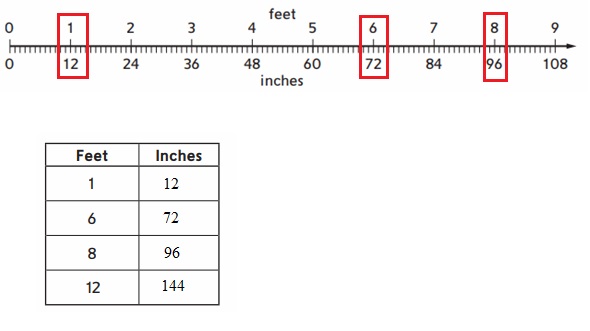
Explanation :
In the above figure the values of feet to inches is marked for respective given values .
As, we know
1 Feet = 12 inches
12 feet = ( 12 ) ( 12) inches = 144 inches .

Question 2.

Answer:

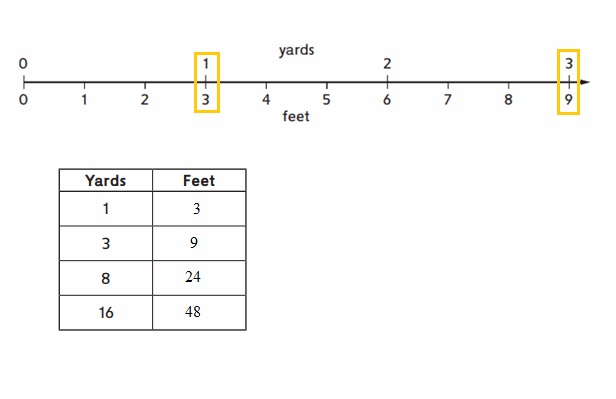
Explanation :
In the above figure the values of Yards to feet is marked for respective given values .
As, we know
1 yard = 3 feet
8 yard = ( 8 ) ( 3) feet = 24 feet .
16 yard = ( 16 ) ( 3) feet = 48 feet .

Question 3.
The king cobra can measure a little over 4 yards in length. The black mamba can reach a length of almost 5 yards. What is the combined length of the two snakes in feet?
Answer: ___ feet
Length of the Cobra = 4 yards
Length of the black mamba = 5 yards
Total length of two snakes = 4 + 5 yards = 9 yards .
1 yard = 3 feet
9 yards = ( 9 ) ( 3) feet = 27 feet .
Therefore, Total length of two snakes = 27 feet .

Question 4.
The Burmese python can be anywhere from 16 to 23 feet long. What is the difference in length in inches between the longest and shortest Burmese python?
Answer: __ inches
Length of Longest Burmese python = 23 feet
Length of shortest Burmese python = 16 feet
Difference between the longest and shortest Burmese python = 23 – 16 feet = 7 feet .
As, we know
1 Feet = 12 inches
7 feet = ( 7 ) ( 12) inches = 84 inches .
Therefore, Difference between the longest and shortest Burmese python = 84 inches .

Practice

Question 5.
Write 4,857 in words.
Answer:
4,857 = Four Thousand, Eight Hundred and Fifty seven .

Question 6.
Write 14,066 in words.
Answer:
14,066 = Fourteen Thousand and Sixty Six .

Everyday Math Grade 4 Home Link 1.11 Answer Key

Line Segments, Lines, and Rays

Question 1.
List at least 5 things in your home that remind you of line segments.
Answer:
Pencil ,  Scale , Table Side , Rod and String .
Explanation :
A line segment is defined as the portion of a line that has two end points.

Use a straightedge to complete Problems 2 and 3.

Question 2.
a. Draw and label line EF.
Answer:

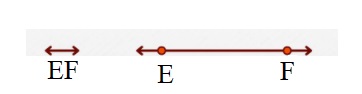
Explanation :
A line is defined by two points and is written as shown below with an arrowhead .

b. Draw and label line segment EF.
Answer:

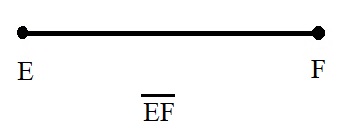
Explanation :
Line segments are represented by a single overbar with no arrowheads over the letters representing the two endpoints.
The line segment Represented as \(\overline{E F}\)

c. Explain how your drawings of line EF and line segment EF are different.
Answer:
Line :
A line is a Straight path of points that goes on without end in both directions .

Line Segment :
A Line segment is a part of a line that includes two end points and all the points between them , it is represented as \(\overline{E F}\) .

Question 3.
a. Draw and label ray SR.
Answer:

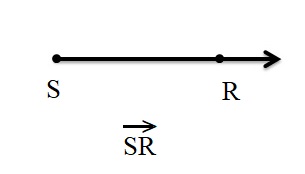
Explanation :
A ray is a part of line that as one end point and goes on without end in one direction . It is represented as \(\overrightarrow{S R}\)

b. Anita says ray SR can also be called ray RS. Do you agree? Explain.
Answer:
No, I disagree . because its endpoint is named first while labeling it .
Explanation :
Ray SR can not be called RS because rays only go in one direction is the ray were RS it would be going the opposite direction or ray SR.
In ray RS, these points are swapped. That is, the initial point is R while the terminal point is S. So, ray RS is oppositely oriented to SR. Hence, ray SR should not be called ray RS.

Question 4.

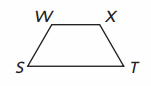
Name the parallel line segments.
Answer:
\(\overline{W X}\) ll \(\overline{S T}\)
Explanation :
Parallel lines are the lines that do not intersect or meet each other at any point in a plane. They are always parallel and are at equidistant from each other.

Practice

Question 5.

Answer:

Question 6.

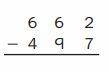
Answer:

Question 7.

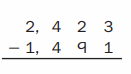
Answer:

Everyday Math Grade 4 Home Link 1.12 Answer Key

Angles and Quadrilaterals

Use a straightedge to draw the geometric figures.

Question 1.
Draw 2 examples of a rectangle.

Answer:

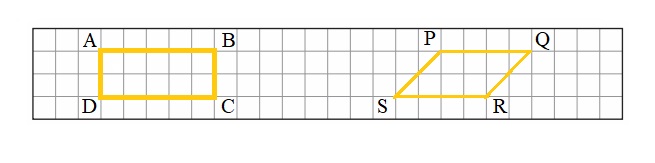
ABCD and PQRS are two rectangles .
Explanation :
A rectangle is a 2D shape in geometry, having 4 sides and 4 corners. Its two sides meet at right angles. Thus, a rectangle has 4 angles, each measuring 90 ̊. The opposite sides of a rectangle have the same lengths and are parallel.

Question 2.
Draw 2 examples of a right triangle.

Answer:

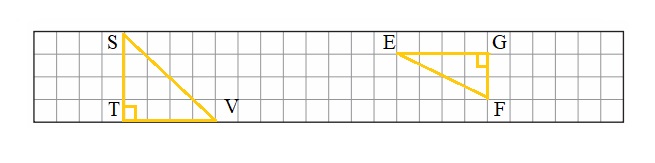
▷STV and ▷EGF are two right triangles .
Explanation :
Right Triangle. Right Triangle. A right triangle is a triangle with one right angle (one angle equal to 90°). The side opposite the right angle (the longest side) is called the hypotenuse. The remaining two sides (the sides that intersect to determine the right angle) are called the legs of the right triangle.

Question 3.
How are the shapes in Problems 1 and 2 similar? How are they different?
Answer:
Rectangle and Triangle have right angles and perpendicular lines .
Rectangle and Triangle have different number of sides , vertices and Right angles .

Question 4.
a. Draw right angle DEF.
b. What is the vertex of the angle? Point ___
c. What is another name for ∠DEF? ___
Answer:
a.

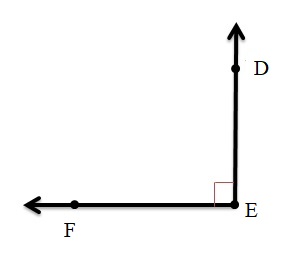
b. The Vertex of the angle is E.
c. The another name for ∠DEF is ∠FED

Question 5.
Draw an angle that is larger than a right angle. Label the vertex K.
Answer:

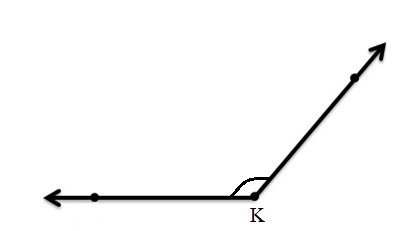
∠k is a obtuse angle .
Explanation :
An obtuse angle is a type of angle that is always larger than 90° but less than 180°. In other words, it lies between 90° and 180°.

Practice

Use U.S. traditional subtraction.

Question 6.
___ = 756 – 348
Answer:
408 = 756 – 348

Question 7.
700 – 450 = ___
Answer:
700 – 450 = 350 .

Question 8.
7,942 – 3,887 = __
Answer:
7,942 – 3,887 = 4055

Everyday Math Grade 4 Home Link 1.13 Answer Key

Finding the Perimeter

Family Note In class, students developed some rules, or formulas, for finding the perimeter
of a rectangle. Here are three possible formulas:
• Add the measures of the four sides: perimeter of a rectangle = length + length + width + width. This formula can be abbreviated as: p = l + l + w + w.
• Add the two given sides and double the s um: perimeter of a rectangle = 2 ∗ (length + width). This formula can be abbreviated as: p = 2 ∗ (l + w).
• Double the length, double the width, and then add: perimeter of a rectangle = (2 ∗ length) + (2 ∗ width). This formula can be abbreviated as: p = 2l + 2w.

In all of the formulas, the letter p stands for the perimeter of a rectangle, the letter l stands for the length of the rectangle, and the letter w stands for the width of the rectangle.

Find the perimeters of the rectangles below.

Question 1.

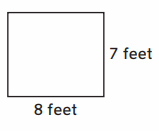
Perimeter: ___ feet
Answer :
Perimeter = 30 feets
Explanation :
Length of the Rectangle = 8 feet
Width of the Rectangle = 7 feet
perimeter of a rectangle = 2 ∗ (length + width) = 2 ∗ ( 8 + 7 ) = 2 ∗ (15) = 30 feets

Question 2.

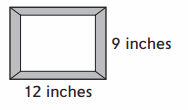
Perimeter: ___ inches
Answer :
Perimeter = 42 inches
Explanation :
Length of the Rectangle = 12 inches
Width of the Rectangle = 9 inches
perimeter of a rectangle = 2 ∗ (length + width) = 2 ∗ ( 12 + 9 ) = 2 ∗ (21) = 42 inches

Question 3.

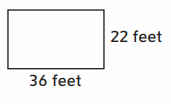
Perimeter: ___ feet
Answer :
Perimeter = 116 feet
Explanation :
Length of the Rectangle = 36 feet
Width of the Rectangle = 22 feet
perimeter of a rectangle = 2 ∗ (length + width) = 2 ∗ ( 36 + 22 ) = 2 ∗ (58) = 116 feet

Question 4.

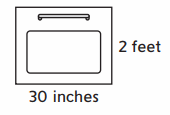
Perimeter: __ inches
Answer :
Perimeter = 108 inches
Explanation :
1 foot = 12 inches
Length of the Rectangle = 30 inches
Width of the Rectangle = 2 feet = 2 ∗ 12 = 24 inches
perimeter of a rectangle = 2 ∗ (length + width) = 2 ∗ ( 30 + 24 ) = 2 ∗ (54) = 108 inches

Question 5.
The perimeter of a garden is 42 feet. The length is 15 feet. What is the width?
Width: __ feet
Answer :
Explanation :
Perimeter of the Rectangle garden = 42 feet
Length of the Rectangle = 15 feet
Width of the Rectangle = x feet
perimeter of a rectangle = 42 = 2 ∗ (length + width) = 2 ∗ (15 + x )
42 = 30 + 2x
42 – 30 = 2x
2x = 12
x = 6 feet
Therefore Width of the Rectangle = 6 feet .