Everyday Mathematics 2nd Grade Answer Key Unit 9 Equal Shares and Whole Number Operations
Everyday Mathematics Grade 2 Home Link 9.1 Answers
Equal Shares
Family Note
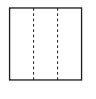
In this lesson your child divided shapes into 2, 3, or 4 equal parts and used words to first name 1 equal part and then to name all of the equal parts together. For example, the square at the right is divided into 3 equal parts.
Each of the parts can be named one-third, 1 -third, or 1 out of 3 equal parts. All of the parts together can be named three-thirds, 3-thirds, or 3 out of 3 equal parts. Although your child may have had experience with standard notation for fractions (\(\frac{1}{3}\), \(\frac{3}{3}\), and so on), the formal introduction of standard notation occurs in third grade.
Question 1.
Divide this square into 2 equal parts.

Circle names for 1 part.
one-half
1-half
2 out of 3 equal parts
1 out of 2 equal parts
Circle names for all of the parts.
1 out of 3 equal parts
2-halves
two-halves
2 out of 2 equal parts
Answer:
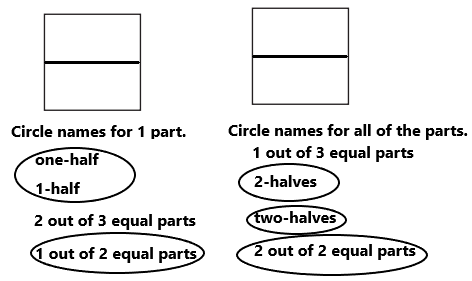
Explanation:
Square is a plane figure with four equal straight sides and four right angles. In the above image we can observe square is divided into two equal parts. Each of the part can be named as one-half, 1-half, 1 out of 2 equal parts. All of the parts can be named as 2 halves, two-halves, 2 out of 2 equal parts. Draw a circle for these names.
Question 2.
Divide this square into 4 equal parts.

Circle names for 1 part.
1 out of 4 equal parts
1- fourth
1 out of 3 equal parts
one- quarter
Circle names for all of the parts.
whole
four-fourths
one-quarter
4 out of 4 equal parts
Answer:
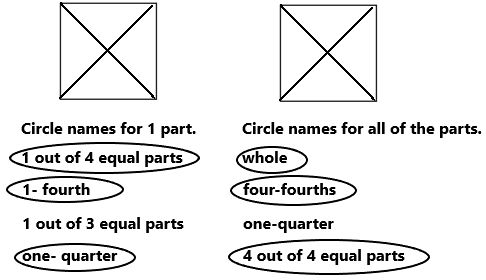
Explanation:
Square is a plane figure with four equal straight sides and four right angles. In the above image we can observe square is divided into four equal parts. Each of the part can be named as 1 out of 4 equal parts, 1- fourth, one-quarter. All of the parts can be named as whole, four-fourths, 4 out of 4 equal parts. Draw a circle for these names.
Everyday Ma
th Grade 2 Home Link 9.2 Answer Key
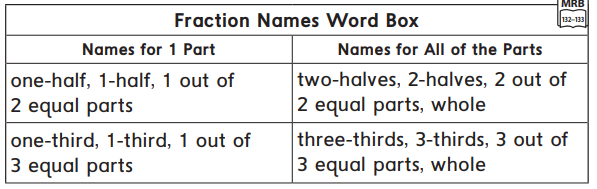
Fraction Names
Family Note
In today’s lesson your child used pattern blocks to divide shapes and then used fraction words to name the equal parts. As you work through the activity below, guide your child to use names from the Fraction Names Word Box. Discuss the names of the parts of each shape.
Question 1.
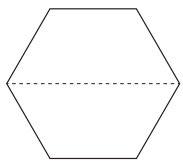
Write the name for 1 part.
______________
Write the name for all of the parts.
________________
Answer:
Explanation:
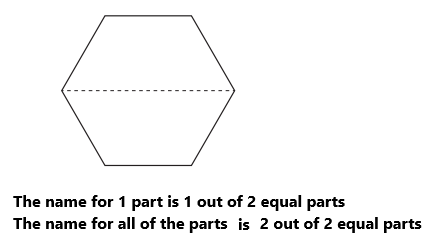
In geometry, a hexagon is a six-sided polygon or 6-gon. The total of the internal angles of any simple hexagon is 720°. In the above image hexagon is divided into two parts. Each of the part can be named as 1 out of 2 equal parts. All of the parts can be named as 2 out of 2 equal parts.
Question 2.
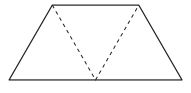
Write the name for 1 part.
______________
Write the name for all of the parts.
________________
Answer:
Explanation:
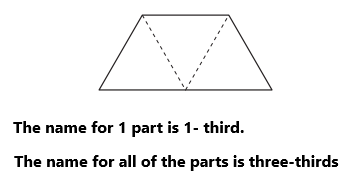
A quadrilateral is a polygon in Euclidean plane geometry with four edges (sides) and four vertices (corners). In the above image quadrilateral is divided into three parts. Each of the part can be named as 1- third. All of the parts can be named as three-thirds.
Everyday Mathematics Grade 2 Home Link 9.3 Answers
Naming Equal Shares
Family Note
In this lesson we continued making and naming equal shares of rectangles and circles. Your child showed and described how to share 3 muffins equally between 2 children, and 5 muffins equally among 4 children. By solving and discussing problems like these, your child will learn appropriate fraction vocabulary, such as 1 out of 2 equal shares, one-half, 1-third, one-quarter, 1-fourth, and one out of four equal shares. Practice making and naming fractional amounts will continue to the end of the year and will lead to a great deal of work with fractions in Third Grade Everyday Mathematics.
Question 1.
Divide the rectangle into 4 equal parts.

Answer:
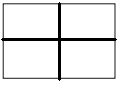
The rectangle into 4 equal parts.
Explanation:
A rectangle is a two-dimensional plane figure with four sides. A rectangle is a four-sided polygon in which the opposite sides are parallel and equal to each other. It is one of the types of quadrilaterals in which all four sides have right angles. It is a special type of parallelogram with equal angles. In the above image we can observe a rectangle with four equal parts.
How could you test that the parts are equal?
Answer:
We have to cut the rectangle out and fold it along the lines to see if the parts are the same size.
Explanation:
In the above problem image we can observe the rectangle with four equal parts. In order to know the parts are equal are not first we have to cut the rectangle out and fold it along the lines to see if the parts are the same size.
Question 3.
Use words to name one of the parts in at least two ways.
Answer:
1 – fourth; one- quarter.
Explanation:
We can name the parts in different ways. Here we can name the parts in two ways as 1-fourth; one- quarter.
Question 4.
Use words to name all of the parts together.
Answer:
Four out of four equal shares; 4-fourths.
Explanation:
All parts together we can name as four out of four equal shares, 4-fourths.
Practice
Question 5.
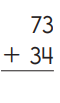
Answer:
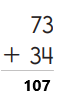
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe two numbers 73 and 34. First add three and four in one’s place right side then we got seven. Keep seven in one’s place and then add seven to three in ten’s place, left side then we got ten write 10 in ten’s place. By adding these two numbers 73 and 34 we got 107.
Question 6.
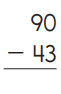
Answer:
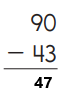
Explanation:
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. The result of a subtraction is called a difference. In the above image we can observe two numbers 90 and 43. In one’s place we can observe zero and three we can’t subtract three from zero so we have to take barrow from ten’s place. Barrow one ten from ten’s place then we got ten subtract three from ten then we got seven. Keep the seven in one’s place. Subtract four from eight in ten’s place then we got four. Keep the four in ten’s place. By subtracting these two numbers we got 47.
Question 7.
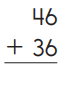
Answer:
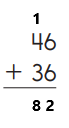
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe two numbers 46 and 36. First add six and six in one’s place right side then we got twelve. Keep two in one’s place and then add one to four in ten’s place, left side then we got five. Add five with three then we got eight write 8 in ten’s place. By adding these two numbers 46 and 36 we got 82.
Everyday Math Grade 2 Home Link 9.4 Answer Key
Measuring Lengths
Family Note
Today your child measured life-size pictures of objects to the nearest inch and half-inch. Because standard notation for fractions (\(\frac{1}{2}\), \(\frac{1}{3}\)) has not been introduced, we recorded half-inch measures with fraction words such as one-half or 1-half. Pick a few objects and take turns with your child measuring each one to the nearest inch and half-inch. Compare your measurements to ensure they are the same.
Cut out the 6-inch ruler below. Use it to measure these line segments to the nearest inch.
Question 1.
____________ About __________ inches
Answer:
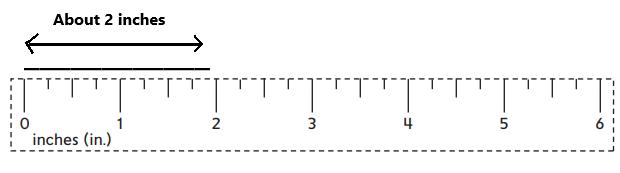
Explanation:
As we can see in the above image, the given line is having a length from zero to two on the scale which is having units as inches. So, the given line is about 2 inches in length.
Measure these line segments to the nearest half-inch.
Question 2.
___________________
About __________ inches
Answer:
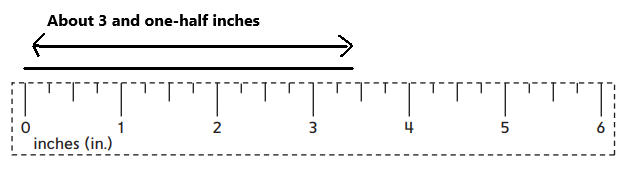
Explanation:
As we can see in the above image, the given line is having a length from zero to 3 and one-half on the scale which is having units as inches. So, the given line is about 3 and one-half inches in length.
Question 3.
____________ About __________ inches
Answer:
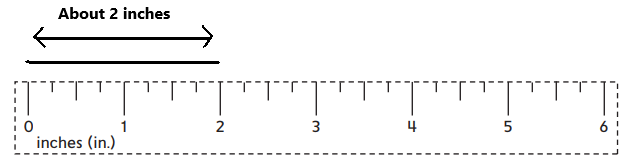
Explanation:
As we can see in the above image, the given line is having a length from zero to two on the scale which is having units as inches. So, the given line is about 2 inches in length.
Measure some objects at home to the nearest half-inch. List the objects and their measurements below.
Question 4.
____________________________
Answer:
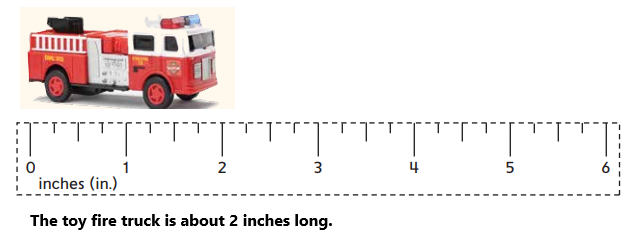
Explanation:
As we can see in the above image, the toy fire truck is having a length from zero to two on the scale which is having units as inches. So, the toy fire truck is about 2 inches in length.
Question 5.
____________________________
Answer:
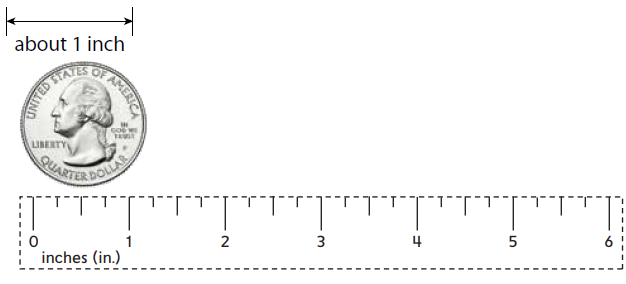
Explanation:
As we can see in the above image, the quarter dollar coin is having a length from zero to one on the scale which is having units as inches. So, the quarter dollar coin is about 1 inches in length.
Question 6.
____________________________
Answer:
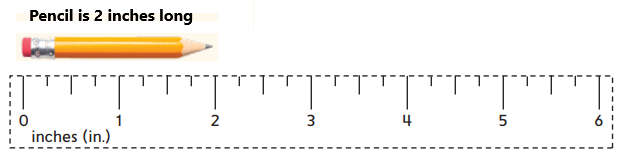
Explanation:
As we can see in the above image, the pencil is having a length from zero to two on the scale which is having units as inches. So, the pencil is about 2 inches in length.
Question 7.
____________________________
Answer:
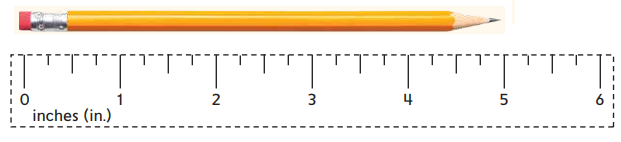
Explanation:
As we can see in the above image, the pencil is having a length from zero to five on the scale which is having units as inches. So, the pencil is about 5 inches in length.

Everyday Mathematics Grade 2 Home Link 9.5 Answers
Place Value
Family Note
In this lesson your child reviewed place value and how it is used to determine the value of digits in numbers. For example, the 5 in 503 is worth 5 hundreds, or 500, because it is in the hundreds place. The 5 in 258 is worth 5 tens, or 50, because it is in the tens place.
Your child also used place value to compare numbers. For example, to compare 571 and 528, your child might think, “Both numbers have 5 hundreds. But 571 has 7 tens and 528 has only 2 tens. So 571 is the larger number.”
In Problems 1–2, write the numbers shown by the base-10 blocks.
Question 1.

Answer:
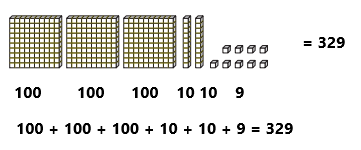
Explanation:
In the above image we can observe base-10 blocks. Now we have to find out the total number of base-10 blocks. First block contains 100 numbers second block contains 100 numbers and third block contains 100 numbers fourth and fifth block contains each 10 numbers and last block contains nine numbers. By adding the above numbers we got 329.
Question 2.

Answer:
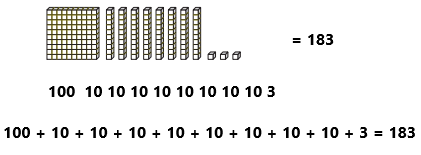
Explanation:
In the above image we can observe base-10 blocks. Now we have to find out the total number of base-10 blocks. First block contains 100 numbers. Next eight blocks contains10 numbers each and last block contains three numbers. By adding the above numbers we got 183.
Question 3.
Read the numbers in Problems 1–2 aloud to someone at home.
Answer:
Three hundred twenty-nine; one hundred eighty-three.
Explanation:
In the above problems 1–2 we got the answers as 329 and 183. 329 can be written as three hundred twenty nine and 183 can be written as one hundred eighty-three.
Question 4.
Write each number in expanded form. Then write < or > in the box to compare the two numbers.
491 = _________________
471 = _________________
491 ![]() 471
471
Answer:

Explanation:
The expanded form of 491 is 400 + 90 + 1.
The expanded form of 471 is 400 + 70 + 1.
Both numbers have 4 hundreds. But 491 has 9 tens and 471 has only 7 tens. So 491 is the larger number.
Write <, >, or =.
Question 5.
295 ![]() 298
298
Answer:

Explanation:
In the above image we can observe both numbers have 2 hundreds and 9 tens. But 295 has 5 ones and 298 has 8 tens. So 298 is the larger number.
Question 6.
387 ![]() 378
378
Answer:

Explanation:
In the above image we can observe both numbers have 3 hundreds. But 387 has 8 tens and 378 has only 7 tens. So 387 is the larger number.
Practice
Add or subtract.

Question 7.
93 + 65 = __________
Answer:
93 + 65 = 158
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 93 and 65. First add three and five in one’s place right side then we got eight. Keep eight in one’s place and then add nine and six in ten’s place, left side then we got fifteen write 15 in ten’s place. By adding these two numbers 93 and 65 we got 158.
Question 8.
80 – 54 = _______
Answer:
80 – 54 = 26
Explanation:
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. The result of a subtraction is called a difference. In the above expression we can observe two numbers 80 and 54. In one’s place we can observe zero and four we can’t subtract four from zero so we have to take barrow from ten’s place. Barrow one ten from ten’s place then we got ten subtract four from ten then we got six. Keep the six in one’s place. Subtract five from seven in ten’s place then we got two. Keep the two in ten’s place. By subtracting these two numbers we got 26.
Question 9.
76 + 26 = _______
Answer:
76 + 26 = 102
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 76 and 26. First add six and six in one’s place right side then we got twelve. Keep two in one’s place and then add one to seven in ten’s place, left side then we got eight. Add eight with two then we got ten write ten in ten’s place. By adding these two numbers 76 and 26 we got 102.
Everyday Math Grade 2 Home Link 9.6 Answer Key
Making Trades to Subtract
Family Note
In this lesson your child learned about subtracting multidigit numbers using base-10 blocks. Your
child also used ballpark estimates to check whether answers made sense. When using base-10 blocks
to subtract, children first check if they need to make any trades. All trades are made before any
subtraction is done. Trading first allows children to concentrate on one thing at a time.
Example: 62 – 36 = ?
- Make a ballpark estimate: 62 is close to 60, and 36 is close to 40, so one estimate is 60 – 40 = 20.
- Sketch 62 using base-10 shorth and:
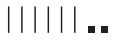
- Are there enough longs and cubes to remove 3 longs and 6 cubes (36)? No, so you need to trade.
- Trade 1 long for 10 cubes:
- Do es the sketch still show 62? Yes.
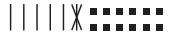
- Can we remove the blocks now to help subtract 36? Yes.
- Remove them.
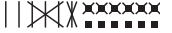
- Count the longs and cubes that are left. The answer is 26.
- Check to see whether the answer makes sense. The ballpark estimate of 20 is close to the answer of 26, so 26 is a reasonable answer.
Question 1.
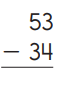
Ballpark estimate:
Sketch 53 using base-10 shorthand. Solve the problem. Show your work.
Answer:
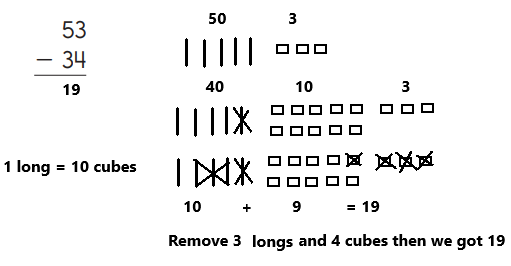
Explanation:
Make a ballpark estimate 53 is close to 50, and 34 is close to 30, so one estimate is 50 – 30 = 20.
Sketch 53 using base-10 shorthand as we can observe in the above image. There are 5 longs and 3 cubes ,1 long represents the value 10
While using base-10 blocks for subtraction, first check if there is need to make any trades because all trades are made before any
subtraction is done. Trading first allows to concentrate on one thing at a time.
There are no enough longs and cubes to remove 3 longs and 4 cubes (34) ,so we need to trade. Trade 1 long for 10 cubes. The sketch still showing 53 as we can can observe in the above image.
Remove the blocks to subtract 34. Cross out 3 longs and 4 cubes. Then count the longs and cubes that are left. 1 long and 9 cubes left. The answer is 19.
The ballpark estimate of 20 is close to the answer of 19, so 19 is a reasonable answer.
Question 2.
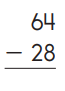
Ballpark estimate:
Sketch 64 using base-10 shorthand. Solve the problem. Show your work.
Answer:
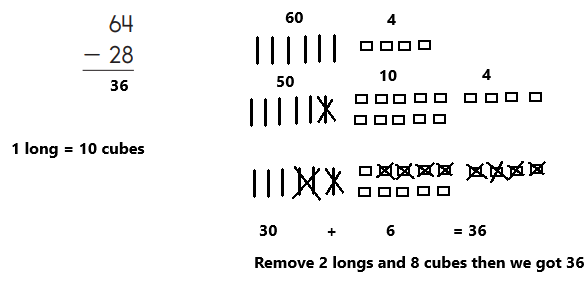
Explanation:
Make a ballpark estimate 64 is close to 60, and 28 is close to 30, so one estimate is 60 – 30 = 30.
Sketch 64 using base-10 shorthand as we can observe in the above image. There are 6 longs and 4 cubes ,1 long represents the value 10
While using base-10 blocks for subtraction, first check if there is need to make any trades because all trades are made before any
subtraction is done. Trading first allows to concentrate on one thing at a time.
There are no enough longs and cubes to remove 2 longs and 8 cubes (28) ,so we need to trade. Trade 1 long for 10 cubes. The sketch still showing 64 as we can can observe in the above image.
Remove the blocks to subtract 28. Cross out 2 longs and 8 cubes. Then count the longs and cubes that are left. 3 long and 6 cubes left. The answer is 36.
The ballpark estimate of 30 is close to the answer of 36, so 36 is a reasonable answer.
Explain to someone how you know your answers make sense.
Answer:
Everyday Mathematics Grade 2 Home Link 9.7 Answers
Expand-and Trade Subtraction
Family Note
In this lesson your child subtracted multidigit numbers using expand-and-trade subtraction. Instead of using base-10 blocks, your child used expanded form to think about making trades. Your child continued to use ballpark estimates to check whether answers made sense.
Example: 62 – 36 = ?
- Write a number sentence to show a ballpark estimate: 60 – 40 = 20.
Write each number in expanded form.
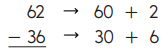
- Look at the 10s and 1s. Can you subtract without making trades? No; so trade 1 ten for 10 ones. Cross out 60 (6 tens) and replace it with 50 (5 tens). Cross out 2 (2 ones) an d replac e it wit h 12 (12 ones). Then subtract.
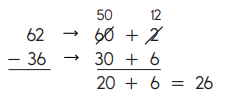
Add the tens and ones to find the total: 20 + 6 = 26. So 62 – 36 = 26. - Compare your answer to your estimate: 20 is close to 26, so 26 is a reasonable answer.
Use expand- and-trade subtraction to solve. Use a ballpark estimate to check your answer.
Question 1.
55 – 37 = ?
Ballpark estimate: ___________
55 – 37 = ____________
Answer:
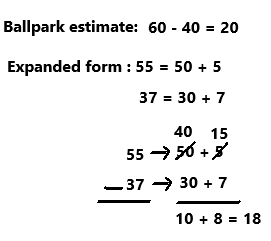
55 – 37 = 18
Compare answer to Ballpark estimate: 20 is close to 18, so 18 is a reasonable answer.
Explanation:
We have an expression 55- 37 for this expression we have to perform subtraction operation.
Consider 55 is close to 60 and 37 is close to 40
First take a number sentence to show a ballpark estimate 60 – 40 = 20.
Then write each number in expanded form 55 = 50 + 5
37 = 30 + 7
Look at the 10s and 1s. We can’t subtract without making trades. So trade 1 ten for 10 ones. Cross out 50 (5 tens) and replace it with 40 (4 tens). Cross out 5 (5 ones) and replace it with 15 (15 ones). Then perform subtraction operation as we can observe in the above answer.
Add the tens and ones to find the total 10 + 8 =18. So 55 – 37 = 18.
Compare answer to Ballpark estimate: 20 is close to 18, so 18 is a reasonable answer.
Question 2.
81 – 28 = ?
Ballpark estimate: ___________
81 – 28 = ____________
Answer:

Compare answer to Ballpark estimate: 50 is close to 53, so 53 is a reasonable answer.
Explanation:
We have an expression 81 – 28 for this expression we have to perform subtraction operation.
Consider 81 is close to 80 and 28 is close to 30
First take a number sentence to show a ballpark estimate 80 – 30 = 50.
Then write each number in expanded form 81 = 80 + 1
28 = 20 + 8
Look at the 10s and 1s. We can’t subtract without making trades. So trade 1 ten for 10 ones. Cross out 80 (8 tens) and replace it with 70 (7 tens). Cross out 1(1 one) and replace it with 11 (11 ones). Then perform subtraction operation as we can observe in the above answer.
Add the tens and ones to find the total 50 + 3 = 53. So 81 – 28 = 53.
Compare answer to Ballpark estimate: 50 is close to 53, so 53 is a reasonable answer.
Everyday Math Grade 2 Home Link 9.8 Answer Key
Coin Combinations
Family Note
In today’s lesson children practiced writing money amounts in cents notation and dollar-and-cents notation. In Problem 1, for example, your child might write the value of 10 pennies as 10¢ or $0.10. Your child also showed two different ways to pay for a single item. For example, your child might have shown 62¢ with 2 quarters, 1 dime, and 2 pennies or with 4 dimes, 4 nickels, and 2 pennies. For Problem 2, help your child find items costing less than 99¢ in newspaper or magazine ads and find different combinations of coins to pay for the items.
Question 1.
Pretend that you have 10 of each kind of coin. How much money would you have?
Fill in the blanks.
10 pennies = ____________
10 nickels = ____________
10 dimes = ____________
10 quarters = ____________
Answer:
10 pennies = 10¢ or $0.10
10 nickels = 50¢ or $0.50
10 dimes =100¢ or $1.00
10 quarters =250¢ or $2.50
Explanation:
As we know that 1 penny is equal to 1 cent or 1 dollar is equal to 100 penny, or 100 cent. Then 10 pennies = 10¢ or $0.10.
1 nickel is equal to 5¢ or 1$ is equal to 20 nickels. Then 10 nickels = 50¢ or $0.50.
1 dime is equal to 10¢ or 1 dime is equal to 0.1$. Then 10 dimes = 100¢ or $1.00.
1 quarter is equal to 25¢ or 1 quarter is equal to 0.25$. Then 10 quarters = 250¢ or $2.50.
Question 2.
Find two ads in a newspaper or magazine for items that cost less than 99¢ each.
- Ask for permission to cut out the ads.
- Cut them out and paste or tape them onto the back of this page.
- Draw coins to show two different ways to pay for each item with exact change.
(If you can’t find ads, draw pictures of items and prices on the back of this page. )
Answer:

Price is 50 cents

Price is 30 cents
Explanation:
First ad is having a burger which costs 50 cents or equivalent to 10 nickels. We can pay in either way.
Second ad is having nuts which costs 30 cents or equivalent to 6 nickels. We can pay in either way.
Everyday Mathematics Grade 2 Home Link 9.9 Answers
Estimating Total Cost
Family Note
In this lesson we worked on a problem in which your child pretended to be at a store and needed to estimate the total cost of selected items using mental math. When you are in a store together, choose two or three items and ask your child to try to estimate the total cost without using pencil and paper. Encourage the use of “close-but-easier” numbers for each item to make it easier to find the total cost using mental math.
For each problem, pretend you are at a store and do not have a calculator or pencil and paper.
Question 1.
You have $1. You want to buy a toy for 59¢ and an apple for 49¢. Do you have enough money? Tell why or why not.
Answer:
No. 59¢ is almost 60¢, and 49¢is almost 50¢. 60¢+ 50¢ is more than $1.
Explanation:
We have 1$ and we have to buy a toy for 59¢ and an apple for 49¢. We don’t have enough money because 59¢ is almost equal to 60¢ and 49¢ is almost equal to 50¢. ADD 60¢ and 50¢ is equal to 110¢, which is more than $1.
Question 2.
You have $50. You want to buy a radio for $32, headphones for $18, and a calculator for $6. Do you have enough money? Tell why or why not.
Answer:
No. 30 + 10 = 40 and 2 and 8 make another 10, so the total for the radio and headphones is $50. I couldn’t buy the calculator, too.
Explanation:
We have $50 and we have to buy a radio for $32 and headphones for $18 and a calculator for $6. We don’t have enough money because $30 and $10 make 40$ and 2 and 8 make another $10. So the total for the radio and headphones is $50. We can buy radio and headphones but we cant buy calculator with $50.
Practice
Add or subtract.
Question 3.
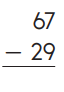
Answer:
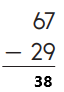
Explanation:
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. The result of a subtraction is called a difference. In the above image we can observe two numbers 67 and 29. In one’s place we can observe seven and nine we can’t subtract nine from seven so we have to take barrow from ten’s place. Barrow one ten from ten’s place then we got seventeen subtract nine from seventeen then we got eight. Keep the eight in one’s place. Subtract two from five in ten’s place then we got three. Keep the three in ten’s place. By subtracting these two numbers we got 38.
Question 4.
35 + 56 = __________
Answer:
35 + 56 = 91
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 35 and 56. First add five and six in one’s place right side then we got eleven. Keep one in one’s place and then add one to three in ten’s place, left side then we got four. Add four with five then we got nine write nine in ten’s place. By adding these two numbers 35 and 56 we got 91.
Question 5.
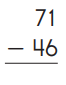
Answer:
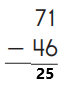
Explanation:
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. The result of a subtraction is called a difference. In the above image we can observe two numbers 71 and 46. In one’s place we can observe one and six we can’t subtract six from one so we have to take barrow from ten’s place. Barrow one ten from ten’s place then we got eleven subtract six from eleven then we got five. Keep the five in one’s place. Subtract four from six in ten’s place then we got two. Keep the two in ten’s place. By subtracting these two numbers we got 25.
Everyday Math Grade 2 Home Link 9.10 Answer Key
Two Equal Groups
Family Note
In this lesson your child solved problems involving 2 equal groups. In some of the problems, your child needed to find the total number of objects in 2 equal groups.
Example: There are 2 packages of water bottles. Each package has 6 bottles.
How many bottles are there in all?
Answer: 12 bottles
Your child can use doubles facts to help solve these problems. For the above problem, your child might think “What is the double of 6? The double of 6 is 12 because 6 + 6 = 12.”
In other problems, your child needed to share items equally into 2 groups.
Example: You have 10 dishes that you want to put in 2 equal piles.
How many dishes should you put in each pile?
Answer: 5 dishes
Your child can also use doubles facts to help solve these problems. For the above problem, your child might think “Which doubles fact has 10 as the sum? It’s 5 + 5 = 10, so there are 5 in each pile.”
Solve each problem and write a number model.
Question 1.
A space alien has 2 hands with 7 fingers on each hand. How many fingers does the space alien have in all?
_________ fingers
Addition number model: _____________
Answer:
Space alien has 14 fingers.
Addition number model : 7 + 7 = 14
Explanation:
A space alien has two hands with seven fingers on each hand. We have to find out the total number of fingers does space alien have in all. To solve the problem we have to use doubles facts. The double of seven is fourteen because 7 + 7 = 14. Space alien has 14 fingers.
Question 2.
You have 8 shells to give to 2 friends. You give the same number to each friend. How many shells does each get?
___________ shells
Addition number model: _____________
Answer:
Two friends got 4 shells each.
Addition number model: 4 + 4 = 8
Explanation:
We have eight shells to give to two friends. We have to give equal number of shells to each friend. To solve the problem we have to use doubles facts. The double fact eight as the sum. It’s 4 + 4 = 8. So there are 4 shells to each friend.
Practice
Add or subtract.
Question 3.
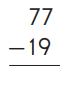
Answer:
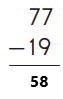
Explanation:
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. The result of a subtraction is called a difference. In the above image we can observe two numbers 77 and 19. In one’s place we can observe seven and nine we can’t subtract nine from from seven so we have to take barrow from ten’s place. Barrow one ten from ten’s place then we got seventeen subtract nine from seventeen then we got eight. Keep the eight in one’s place. Subtract one from six in ten’s place then we got five. Keep the five in ten’s place. By subtracting these two numbers we got 58.
Question 4.
47 + 83 = __________
Answer:
47 + 83 = 130
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 47 and 83. First add seven and three in one’s place right side then we got ten. Keep zero in one’s place and then add one to four in ten’s place, left side then we got five. Add five with eight then we got thirteen write 13 in ten’s place. By adding these two numbers 47 and 83 we got 130.
Question 5.
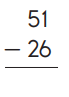
Answer:
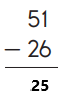
Explanation:
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. The result of a subtraction is called a difference. In the above image we can observe two numbers 51 and 26. In one’s place we can observe one and six we can’t subtract six from one so we have to take barrow from ten’s place. Barrow one ten from ten’s place then we got eleven subtract six from eleven then we got five. Keep the five in one’s place. Subtract two from four in ten’s place then we got two. Keep the two in ten’s place. By subtracting these two numbers we got 25.
Everyday Mathematics Grade 2 Home Link 9.11 Answers
5s and 10s
Family Note
In this lesson your child solved problems involving multiples of 10 and 5. A multiple of 5 is the answer to a multiplication problem involving 5 and any counting number. For example, 20 is a multiple of 5 because 5 × 4 = 20. The number 20 is also a multiple of 10 because 10 × 2 = 20.
The multiples of a number are also the skip counts of that number.
Multiples of 5: 5, 10, 15, 20, . . .
Multiples of 10: 10, 20, 30, 40, . . .
Dimes and nickels were used as a context for finding multiples of 5 and 10. Your child can solve the problems below by skip counting.
Question 1.
2 nickels = _________ cents 2 [5s] is _________ 2 × 5 = _________
6 nickels = _________ cents 6 [5s] is _________ 6 × 5 = _________
Answer:

Explanation:
From the question, we got to know that nickels were used as a context in multiples of 5.
So, 1 nickel represents a multiple of 5 which is in cents , it means 1nickel=1 x 5 cents =5 cents.
In the question, it was asked to calculate 2 nickels. So, 2nickels = 2 x 5 cents = 10 cents.
In the question, it was asked to calculate 6 nickels. So, 6nickels = 6 x 5 cents = 30 cents.
Question 2.
4 dimes = _________ cents 4 [10s] is _________ 4 × 10 = _________
7 dimes = _________ cents 7 [10s] is _________ 7 × 10 = _________
Answer:
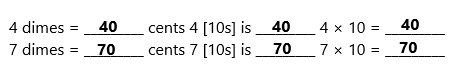
Explanation:
From the question, we got to know that dimes were used as a context in multiples of 10.
So, 1 dime represents a multiple of 10 which is in cents , it means 1dime=1 x 10 cents =10 cents.
In the question, it was asked to calculate 4 dimes. So, 4 dimes = 4 x 10 cents = 40 cents.
In the question, it was asked to calculate 7 dimes. So, 7 dimes = 7 x 10 cents = 70 cents.
Question 3.
8 dimes = _________ cents 8 [10s] is _________ 8 × 10 = _________
8 nickels = _________ cents 8 [5s] is _________ 8 × 5 = _________
Answer:

Explanation:
From the question, we got to know that nickels were used as a context in multiples of 5 and dimes were used as a context in multiples of 10.
So, 1 dime represents a multiple of 10 which is in cents , it means 1dime=1 x 10 cents =10 cents.
So, 1 nickel represents a multiple of 5 which is in cents , it means 1nickel=1 x 5 cents =5 cents.
In the question, it was asked to calculate 8 dimes. So, 8dimes = 8 x 10 cents = 80 cents.
In the question, it was asked to calculate 8 nickels. So, 8nickels = 8 x 5 cents = 40 cents.
Practice
Add or subtract.
Question 4.
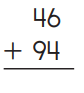
Answer:
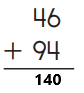
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe two numbers 46 and 94. First add six and four in one’s place right side then we got ten. Keep zero in one’s place and add one to four in ten’s place left side then we got five. Add five with nine then we got fourteen write 14 in ten’s place. By adding these two numbers 46 and 94 we got 140.
Question 5.
92 – 49 = ________
Answer:
92 – 49 = 43
Explanation:
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. The result of a subtraction is called a difference. In the above expression we can observe two numbers 92 and 49. In one’s place we can observe two and nine we can’t subtract nine from two so we have to take barrow from ten’s place. Barrow one ten from ten’s place then we got twelve subtract nine from twelve then we got three. Keep the three in one’s place. Subtract four from eight in ten’s place then we got four. Keep the four in ten’s place. By subtracting these two numbers we got 43.
Question 6.
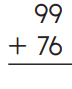
Answer:
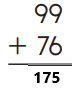
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe two numbers 99 and 76. First add nine and six in one’s place right side then we got fifteen. Keep five in one’s place and then add one to nine in ten’s place, left side then we got ten. Add ten with seven then we got seventeen write 17 in ten’s place. By adding these two numbers 99 and 76 we got 175.