Everyday Mathematics 2nd Grade Answer Key Unit 7 Whole Number Operations and Measurement and Data
Everyday Math Grade 2 Home Link 7.1 Answer Key
Missing Addends
Family Note
In this lesson your child used mental strategies to find differences between 2-digit numbers and larger multiples of 10. For example, your child found what number added to 44 equals 50. (The answer is 6.) In Problems 1–2 your child will find the difference between a number and the next larger multiple of 10. In Problem 3 your child will find different combinations of numbers that add to 70. If your child has difficulty with this problem, suggest first adding 1s to the first number in each combination to find the next-larger multiple of 10. For example, add 2 to 48 to make 50. Then add 20 (or two 10s) to 50 to make 70. Finally, add 2 + 20 to find the answer, 22. So 48 + 22 = 70.
Please return this Home Link to school tomorrow.
Question 1.
4 + __ = 10
10 = 3 + __
__ + 5 = 10
10 = __ + 1
8 + __ = 10
Answer:
4 + 6 = 10
10 = 3 + 7
5 + 5 = 10
10 = 9 + 1
8 + 2 = 10
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together.
ADD four with six then we got the sum ten.
ADD three with seven then we got the sum ten.
ADD five with five then we got the sum ten.
ADD one with nine then we got the sum ten.
ADD eight with two then we got the sum ten.
Question 2.
54 + __ = 60
90 = 83 + __
75 + __ = 80
40 = 31 + __
__ + 42 = 50
Answer:
54 + 6 = 60
90 = 83 + 7
75 + 5 = 80
40 = 31 + 9
8 + 42 = 50
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together.
ADD 54 with 6 then we got the sum 60.
ADD 83 with 7 then we got the sum 90.
ADD 75 with 5 then we got the sum 80.
ADD 31 with 9 then we got the sum 40.
ADD 42 with 8 then we got the sum 50.
Question 3.
Make 70s. Show someone at home how you did it.
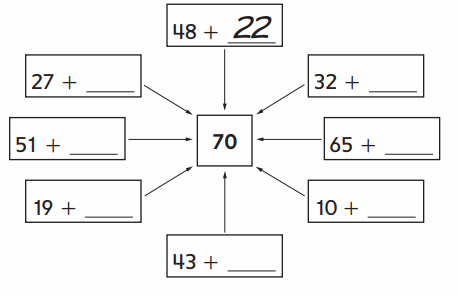
Answer:
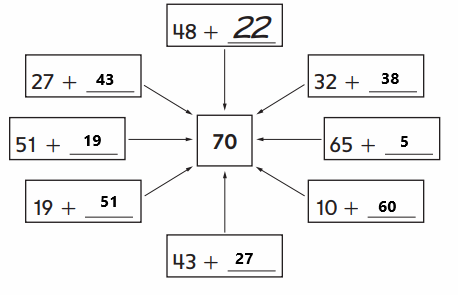
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. By adding 1s to the first number in each combination is used to find the next-larger multiple of 10.
Add 2 to 48 to make 50. Then add 20 (or two 10s) to 50 to make 70. Finally, add 2 + 20 to find the answer, 22. So 48 + 22 = 70.
Add 8 to 32 to make 40. Then add 30 (or three 10s) to 40 to make 70. Finally, add 8 + 30 to find the answer, 38. So 32 + 38 = 70.
Add 5 to 65 to make 70. So 65 +5 = 70.
Add 60 to 10 to make 70. So 10 + 60 = 70.
Add 7 to 43 to make 50. Then add 20 (or two 10s) to 50 to make 70. Finally, add 7 + 20 to find the answer, 27. So 43 + 27 = 70.
Add 1 to 19 to make 20. Then add 50 (or five 10s) to 20 to make 70. Finally, add 1 + 50 to find the answer, 51. So 19 + 51 = 70.
Add 9 to 51 to make 60. Then add 10 (or one 10) to 60 to make 70. Finally, add 9 + 10 to find the answer, 19. So 51 + 19 = 70.
Add 3 to 27 to make 30. Then add 40 (or four 10s) to 30 to make 70. Finally, add 3 + 40 to find the answer, 43. So 27 + 43 = 70.
Everyday Math Grade 2 Home Link 7.2 Answer Key
Adding Three or More Numbers
Family Note
Today your child added more than 2 addends. Changing the order of the addends can make it easier to find the sum. For example, when adding 17, 19, and 23, some people may first calculate 17 + 23, which equals 40, and then add 19 (40 + 19 = 59). For Problems 1–4, help your child look for easy combinations. Before working on Problems 5–10, you might go over the example with your child.
Please return this Home Link to school tomorrow.
For each problem:
- Think about an easy way to add the numbers.
- Write a number model to show the order in which you are adding the numbers.
- Find each sum. Tell someone at home why you added the numbers in that order.
Question 1.
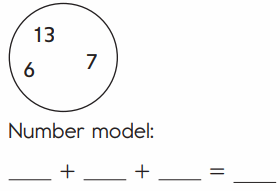
Answer:
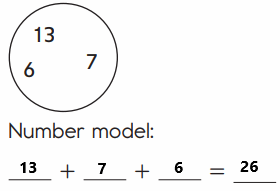
20 + 6 = 26
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. Here we are Changing the order of the addends to find the sum in easy way. We are adding the numbers in a order so we have to write the number model first. The number model for above image is 13 + 7 + 6= 26. First add thirteen and seven then we got twenty, then add twenty with six then we got 26.
Question 2.
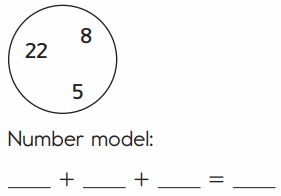
Answer:
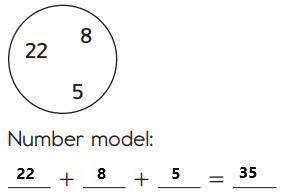
30 + 5 = 35
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. Here we are Changing the order of the addends to find the sum in easy way. We are adding the numbers in a order so we have to write the number model first. The number model for above image is 22 + 8 + 5= 35. First add 22 and 8 then we got 30, then add 30 with 5 then we got 35.
Question 3.
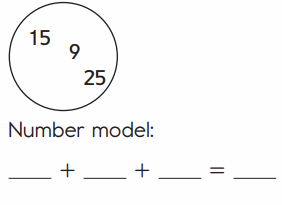
Answer:
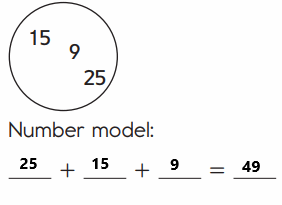
40 + 9 = 49
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. Here we are Changing the order of the addends to find the sum in easy way. We are adding the numbers in a order so we have to write the number model first. The number model for above image is 25 + 15 + 9= 49. First add 25 and 15 then we got 40, then add 40 with 9 then we got 49.
Question 4.
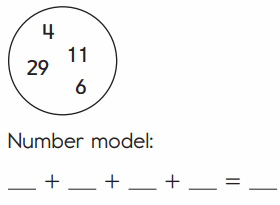
Answer:
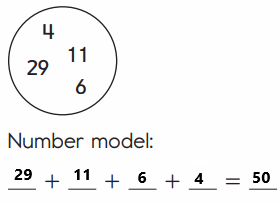
40 + 10 = 50
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. Here we are Changing the order of the addends to find the sum in easy way. We are adding the numbers in a order so we have to write the number model first. The number model for above image is 29 + 11 + 6 + 4 = 50. First add 29 and 11 then we got 40, then add 6 and 4 then we got 10. ADD 40 with 10 then we got 50.
Add. Use the partial-sums method.
Example:
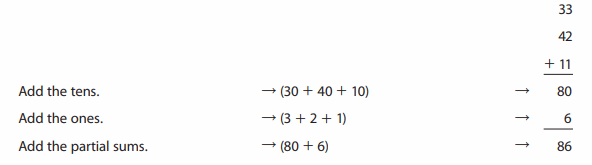
Practice
Question 5.
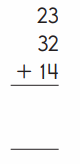
Answer:
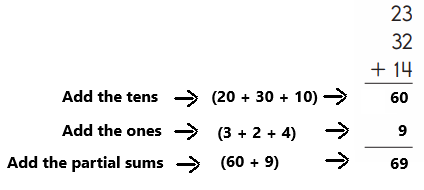
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe three numbers 23,32 and 14. First add the tens (20 + 30 + 10 ). Next add the ones (3 + 2 + 4 ). By adding the tens we got 60 and adding the ones we got 9. By adding the partial sums we got 69 (60 + 9).
Question 6.
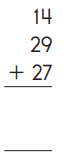
Answer:

Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe three numbers 14, 29 and 27. First add the tens (10 + 20 + 20 ). Next add the ones (4 + 9 + 7 ). By adding the tens we got 50 and adding the ones we got 20. By adding the partial sums we got 70 (50 + 20).
Question 7.
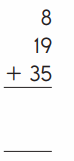
Answer:

Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe three numbers 8, 19 and 35. First add the tens (10+ 30 ). Next add the ones (8 + 9+ 5 ). By adding the tens we got 40 and adding the ones results 22. By adding the partial sums we got 62 (40 + 22).
Question 8.
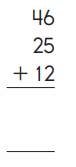
Answer:

Answer:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe three numbers 46, 25 and 12. First add the tens (40 + 20 + 10 ). Next add the ones (6 + 5 + 2 ). By adding the tens we got 70 and adding the ones results 13. By adding the partial sums we got 83 (70 + 13).
Question 9.
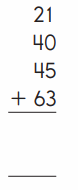
Answer:

Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe three numbers 21, 40, 45 and 14. First add the tens (20 + 40 + 40 + 60 ). Next add the ones (1 + 0 + 5 + 3 ). By adding the tens we got 160 and adding the ones results 9. By adding the partial sums we got 169 (160 + 9).
Question 10.
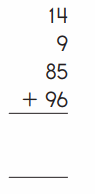
Answer:

Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe three numbers14, 9, 85, 96. First add the tens (10 + 80 + 90 ). Next add the ones (4 + 9 + 5 +6 ). By adding the tens we got 180 and adding the ones results 24. By adding the partial sums we got 204 (180 + 24).
Everyday Math Grade 2 Home Link 7.3 Answer Key
Who Scored More Points?
Family Note
In this lesson your child added three or more 1-digit and 2-digit numbers. As your child completes the problems below, encourage him or her to share the different ways in which the points can be added. Your child might add all the 10s first and then add all the 1s. For example, 20 + 5 + 4 + 6 = 20 + 15 = 35. Your child may also look for combinations of numbers that are easier to add. In Game 1, for example, first add 14 and 6 to get 20 and then add 15 to get 35.
Please return this Home Link to school tomorrow.
Do the following for each problem:
- Add the points for each team.
- Decide which team scored more points.
The team with more points wins the game.
• Circle your answer.
Question 1.
Game 1
Team A:
15 + 1 4 + 6 = __
Team B:
5 + 13 + 7 = __
Who won? A or B
Answer:

Team A scored more points. So Team A won the game.
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe two teams Team A and Team B.
Team A having 15, 14, 6 points. First add 14 with 6 then we got 20. ADD 15 with 20 then we got 35.
Team B having 5, 13, 7 points. First add 13 with 7 then we got 20. ADD 5 with 20 then we got 25.
Team A scored more points. So Team A won the game. Draw a circle for 35.
Question 2.
Game 2
Team A:
12 + 6 + 4 + 8 = ___
Team B:
5 + 10 + 19 + 1 = __
Who won? A or B
Answer:

Team B scored more points. So Team B won the game.
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe two teams Team A and Team B.
Team A having 12, 6, 4, 8 points. First add 12 with 8 then we got 20, next add 6 with 4 then we got 10. Add 20 with 10 then we got 30.
Team B having 5, 10, 19, 1 points. First add 19 with 1 then we got 20. ADD 10 with 20 then we got 30. ADD 5 with 30 then we got 35
Team B scored more points. So Team B won the game. Draw a circle for 35.
Question 3.
Game 3
Team A:
17 + 4 + 5 + 3 = __
Team B:
2 + 1 1 + 9 + 18 = __
Who won? A or B
Answer:
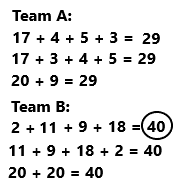
Team B scored more points. So Team B won the game.
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe two teams Team A and Team B.
Team A having 17, 4, 5, 3 points. First add 17 with 3 then we got 20, next add 4 with 5 then we got 9. Add 20 with 9 then we got 29.
Team B having 2, 11, 9, 18, 2 points. First add 11 with 9 then we got 20. ADD 18 with 2 then we got 20. ADD 20 with 20 then we got 40
Team B scored more points. So Team B won the game. Draw a circle for 40.
Question 4.
Game 4
Team A:
7 + 4 + 1 6 + 13 + 5 = ___
Team B:
22 + 9 + 8 + 3 + 1 7 = __
Who won? A or B
Answer:

Team B scored more points. So Team B won the game.
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above image we can observe two teams Team A and Team B.
Team A having 7, 4, 16, 13, 5 points. First add 7 with 13 then we got 20, next add 4 with 16 then we got 20. Add 20 with 20 and 5 then we got 45.
Team B having 22, 9, 8, 3, 17 points. First add 22 with 8 then we got 30. ADD 3 with 17 then we got 20. ADD 30 with 20 and 9 then we got 59
Team B scored more points. So Team B won the game. Draw a circle for 59.
Everyday Math Grade 2 Home Link 7.4 Answer Key
Using Measurement
Family Note
In class today your child measured distances with a yardstick. Talk with your child about measurements you use at your job, around the house, in sports, or in other activities. If you don’t have measuring tools to show your child, you might find pictures of measuring tools online or in a catalog, magazine, or book. Discuss with your child how these tools are used.
Please return this Home Link to school tomorrow.
Question 1.
Talk with people at home about how they use measurements at home, at their jobs, or in other activities.
Answer: The people at my home use measurements for a wide range of activities such as
- Measuring length of a cloth for tailoring
- Measuring level of fuel in tank for continuous running
- Measuring the amount of water used to cook food
- Measuring the length of wall for holding nails or to fix something on it.
Question 2.
Ask people at home to show you the tools they use for measuring. Write the names of some of these tools. Be ready to talk about your list in class.
___ ___
___ ___
___ ___
Answer:
Tailor Measuring Tool

Ruler
 Measuring jar:
Measuring jar:

Explanation:
In the above images we can observe three types of measuring tools. one is tailor measuring tape second one is ruler and third one is measuring jar.
Tailors measuring tape is made for cloth and are used to take measurements of the person for whom the clothing is being made. As such, these tape measures are used to measure around a person’s waist, chest, and hips.
A ruler is an instrument used to measure distances, degrees and determine straight lines. There are many different types of measuring rulers, available in different shapes, sizes and materials. These rulers are used in various occupations and fields of study, such as geometry, printing, technical drawing, building and engineering.
Plastic Measuring Jar 25ml. Measuring Jar is designed to give approximate measurement of ml, in general day to day cooking Preparations of Rice, Sugar, Chana. It Is one of the basic requirements of every kitchen to get the exact taste of every meal.
Question 3.
Look for measurements in pictures, in newspapers, or magazines. For example, an ad might tell the height of a bookcase or how much a container holds. Ask an adult if you may bring the pictures to school for our Measures
All Around Museum. Circle the measurements.
Answer:
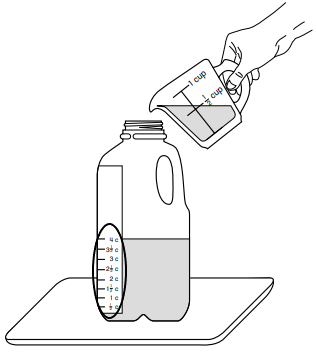
Explanation:
Attach a piece of tape from the bottom to the top of an empty half-gallon container. Fill a measuring cup with a half-cup of water.
Pour the water into the container. Do all of our pouring on a tray to catch the drips. Mark the tape to show how high the water is inside the container. Write 1/2 c next to the mark. Pour another half-cup of water into the container. Mark the tape and write 1 c next to the mark. Mark the tape 1 1/2 c to show 3 half-cups, 2 c for 4 half-cups, 4c for 8 half-cups. Fill the container. Pour the water back into the pitcher.
Practice
Solve.
Question 4.
93 + 1 = __
Answer:
93 + 1 = 94
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 93 and 1. First add three and one in one’s place right side then we got four. Keep four in one’s place and then add zero to nine in ten’s place, left side then we got nine write nine in ten’s place. By adding these two numbers 93 and 1 we got 94.
Question 5.
__ = 6 + 61
Answer:
67 = 6 + 61
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 6 and 61. First add six and one in one’s place right side then we got seven. Keep seven in one’s place and then add zero to six in ten’s place, left side then we got six write six in ten’s place. By adding these two numbers 6 and 61 we got 67.
Question 6.
__ = 26 + 8
Answer:
34 = 26 + 8
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 26 and 8. First add six and eight in one’s place right side then we got fourteen. Keep four in one’s place and then add one to two in ten’s place, left side then we got three write three in ten’s place. By adding these two numbers 26 and 8 we got 34.
Question 7.
5 + 49 = __
Answer:
5 + 49 = 54
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 5 and 49. First add five and nine in one’s place right side then we got fourteen. Keep four in one’s place and then add one to four in ten’s place, left side then we got five write five in ten’s place. By adding these two numbers 5 and 49 we got 54.
Everyday Math Grade 2 Home Link 7.5 Answer Key
Measuring Height
Family Note
In this lesson your child was introduced to a metric unit of length called the meter. One meter is equal to 100 centimeters. We compared metersticks to yardsticks and noticed that 1 meter is a little longer than 1 yard. Then we used tools such as rulers, yardsticks, metersticks, and tape measures to measure lengths. Your child may wonder why there are two standard units—yards and meters—that
are nearly the same size. You may want to explore this issue by searching online for information about the metric and U.S. customary systems of measurement.
If you don’t have tools to measure length with metric units at home, you and your child can cut
pieces of string or strips of paper to match the heights of a table and an adult. Your child can bring
the string or strips to school to measure.
Please return this Home Link to school tomorrow
Question 1.
Work with someone at home to measure the height of a table.
The table is about __ centimeters high.
The table is about __ meters high.
Answer:
The table is about 200 centimeters high.
The table is about 2 meters high.
Explanation:
Centimeter is a metric unit of length, equal to one hundredth of a meter. The table is measured with tape and the table is about 200 centimeters high. In meters the table is about 2 meters high.
Question 2.
Measure the height of an adult.
The adult is about __ centimeters tall.
The adult is about __ meters tall.
Answer:
The adult is about 150 centimeters tall.
The adult is about 1.5 meters tall.
Explanation:
Centimeter is a metric unit of length, equal to one hundredth of a meter. The table is measured with tape and the adult is about 150 centimeters tall. In meters the adult is about 1.5 meters tall.
Question 3.
Are there more centimeters or more meters in your measurements? __ Explain.
Answer:
More centimeters, centimeters are shorter, so it takes more of them to measure the same height.
Explanation:
Centimeter is a metric unit of length, equal to one hundredth of a meter. There are more centimeters in my measurements because centimeters are shorter, so it takes more of them to measure the same height.
Practice
Question 4.
18 + __ = 20
Answer:
18 + 2 = 20
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 18 and 2. First add eight and two in one’s place right side then we got ten. Keep zero in one’s place and then add one to one in ten’s place, left side then we got two write two in ten’s place. By adding these two numbers 18 and 2 we got 20.
Question 5.
__ + 3 = 53
Answer:
50 + 3 = 53
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 50 and 3. First add zero and three in one’s place right side then we got three. Keep three in one’s place and then add zero to five in ten’s place, left side then we got five write five in ten’s place. By adding these two numbers 50 and 3 we got 53.
Question 6.
__ = 86 + 7
Answer:
93 = 86 + 7
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 86 and 7. First add six and seven in one’s place right side then we got thirteen. Keep three in one’s place and then add one to eight in ten’s place, left side then we got nine write nine in ten’s place. By adding these two numbers 86 and 7 we got 93.
Question 7.
8 + 33 = __
Answer:
8 + 33 = 41
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 8 and 33. First add eight and three in one’s place right side then we got eleven. Keep one in one’s place and then add one to three in ten’s place, left side then we got four write four in ten’s place. By adding these two numbers 8 and 33 we got 41.
Everyday Math Grade 2 Home Link 7.6 Answer Key
Comparing Arm Spans
Family Note
In today’s lesson your child measured his or her standing jump and arm span in both centimeters and inches. Help your child compare his or her arm span to someone else’s arm span at home. Also help your child find objects around the house that are about the same length as his or her arm span.
Please return this Home Link to school tomorrow.
My arm span is about __ inches long.
Question 1.
Tell someone at home about how long your arm span is in inches.
Answer: I’ve measured and my arm span is about 36 inches.
Explanation:
An inch is an imperial unit of length, approximately equal to 2.54 centimeters. We can measure arm span in both centimeters and inches. I have measured and my arm span is about 36 inches.
Question 2.
Compare your arm span to the arm span of someone at home. Can you find someone who has a longer arm span than you do? Is there someone at home who has a shorter arm span?
_____ has a longer arm span than I have.
____ has a shorter arm span than I have.
Answer: My father has a longer arm span than I have.
My sister has a shorter arm span than I have.
Explanation:
An inch is an imperial unit of length, approximately equal to 2.54 centimeters. We can measure arm span in both centimeters and inches. I have measured my arm span, My father arm span and My sister arm span. My father has a longer arm span than I have.
My sister has a shorter arm span than I have.
Question 3.
List some objects that are about the same length as your arm span.
Answer: My wardrobe, our mini-fridge, our dining table, our cot have the same length as my arm span.
Explanation:
An inch is an imperial unit of length, approximately equal to 2.54 centimeters. We can measure arm span in both centimeters and inches. Some objects are about the same length of my arm span. My wardrobe, our mini-fridge, our dining table, our cot have the same length as my arm span.
Question 4.
Explain how you know the objects you listed in Problem 3 are about the same length as your arm span.
Answer: I’ve measured with tape and the length of all those objects are nearly of same length as y arm span. Also, when I check with my arm span, they almost match to my arm span length.
Explanation:
An inch is an imperial unit of length, approximately equal to 2.54 centimeters. We can measure arm span in both centimeters and inches. I’ve measured with tape and the length of all those objects are nearly of same length as my arm span. Also, when I check with my arm span, they almost match to my arm span length.
Practice
Solve.
Question 5.
57 + 3 = ___
Answer:
57 + 3 = 60
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 57 and 3. First add seven and three in one’s place right side then we got ten. Keep zero in one’s place and then add one to five in ten’s place, left side then we got six write six in ten’s place. By adding these two numbers 57 and 3 we got 60.
Question 6.
4 + 71 = __
Answer:
4 + 71 = 75
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 4 and 71. First add four and one in one’s place right side then we got five. Keep five in one’s place and then add zero to seven in ten’s place, left side then we got seven write seven in ten’s place. By adding these two numbers 4 and 71 we got 75.
Question 7.
__ = 34 + 9
Answer:
43 = 34 + 9
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 34 and 9. First add four and nine in one’s place right side then we got thirteen. Keep three in one’s place and then add one to three in ten’s place, left side then we got four write four in ten’s place. By adding these two numbers 34 and 9we got 43.
Question 8.
48 + __ = 56
Answer:
48 + 8 = 56
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 48 and 8. First add eight and eight in one’s place right side then we got sixteen. Keep six in one’s place and then add one to four in ten’s place, left side then we got five write five in ten’s place. By adding these two numbers 48 and 8 we got 56.
Everyday Math Grade 2 Home Link 7.7 Answer Key
Interpreting Data
Family Note
In this lesson your child examined classroom data on the length of classmates’ standing jumps. The class found the shortest jump length and the longest jump length and calculated the difference between the lengths. They also made a line plot based on the data.
Please return this Home Link to school tomorrow.
The track team collected these standing-jump data:
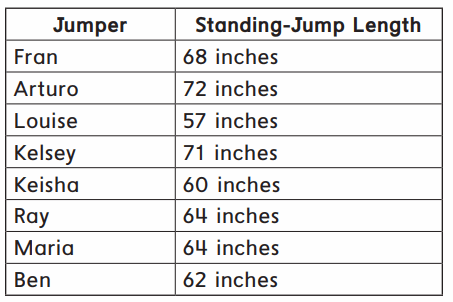
List the inches for each jump in order from shortest to longest.
___, ___, ___, ___, ___, ___, ___, ___
Answer:
The inches for each jump from shortest to longest is 57, 60, 62, 64, 64, 68, 71, 72.
Explanation:
In the above image we can observe jumper name and standing jump length. The data is in the form of inches. An inch is an imperial unit of length, approximately equal to 2.54 centimeters. The inches for each jump from shortest to longest is 57, 60, 62, 64, 64, 68, 71, 72.
Question 2.
What is the shortest jump length? ___ inches
Answer:
57 inches is the shortest jump length.
Explanation:
In the above image we can observe jumper name and standing jump length. The data is in the form of inches. An inch is an imperial unit of length, approximately equal to 2.54 centimeters. In the above table we can observe 57 inches is the shortest jump length by comparing with other standing jump lengths.
Question 3.
What is the longest jump length? __ inches
Answer:
72 inches is the longest jump length.
Explanation:
In the above image we can observe jumper name and standing jump length. The data is in the form of inches. An inch is an imperial unit of length, approximately equal to 2.54 centimeters. In the above table we can observe 72 inches is the longest jump length by comparing with other standing jump lengths.
Question 4.
What is the difference between the longest jump length and the shortest jump length? __ inches
Answer:
72 inches is the longest jump length.
57 inches is the shortest jump length.
The difference between the longest jump length and the shortest jump length is 15 inches.
72 – 57 = 15
Explanation:
In the above image we can observe jumper name and standing jump length. The data is in the form of inches. An inch is an imperial unit of length, approximately equal to 2.54 centimeters. In the above table we can observe 72 inches is the longest jump length and 57 inches is the shortest jump length by comparing with other standing jump lengths. Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. The result of a subtraction is called a difference. The difference between the longest jump length and the shortest jump length is 15 inches.
72 – 57 = 15
Practice
Question 5.
__ = 1 + 97
Answer:
98 = 1 + 97
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 1 and 97. First add one and seven in one’s place right side then we got eight. Keep eight in one’s place and then add zero to nine in ten’s place, left side then we got nine write nine in ten’s place. By adding these two numbers 1 and 97 we got 98.
Question 6.
23 + 6 = __
Answer:
23 + 6 = 29
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 23 and 6. First add three and six in one’s place right side then we got nine. Keep nine in one’s place and then add zero to two in ten’s place, left side then we got two write two in ten’s place. By adding these two numbers 23 and 6 we got 29.
Everyday Math Grade 2 Home Link 7.8 Answer Key
Interpreting Data
Family Note
Today your child represented class arm span data in a frequency table and on a line plot. Line plots like the one below help us organize and display data. Each X in this line plot represents one basketball player. Help your child use the data in the line plot to answer the questions.
Please return this Home Link to school tomorrow.
Ms. Ortiz is a basketball coach. She measured the height of each player on the team. Then she made this line plot.
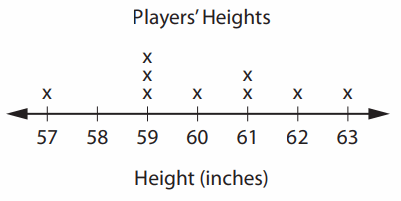
Question 1.
How many players are 61 inches tall? __ players
Answer:
Each X in this line plot represents one basketball player. 2 players are 61 inches tall.
Explanation:
Line plots like the one above help us organize and display data. Each X in this line plot represents one basketball player. The data height is in the form of inches. In the above image we can observe basket players and their height. In this line plot we can see 61 inches in that we can observe two X’s. So two players are 61 inches tall.
Question 2.
How many players are 58 inches tall? __ players
Answer:
Each X in this line plot represents one basketball player. 0 players are 58 inches tall.
Explanation:
Line plots like the one above help us organize and display data. Each X in this line plot represents one basketball player. The data height is in the form of inches. In the above image we can observe basket players and their height. In this line plot we can see 58 inches in that we can observe zero X’s. So zero players are 58 inches tall.
Question 3.
The shortest player is __ inches tall.
Answer:
The shortest player is 57 inches tall.
Explanation:
Line plots like the one above help us organize and display data. Each X in this line plot represents one basketball player. The data height is in the form of inches. In the above image we can observe basket players and their height. The shortest player is 57 inches tall.
Question 4.
The tallest player is __ inches tall.
Answer:
The tallest player is 63 inches tall.
Explanation:
Line plots like the one above help us organize and display data. Each X in this line plot represents one basketball player. The data height is in the form of inches. In the above image we can observe basket players and their height. The tallest player is 63 inches tall.
Question 5.
How many players did Ms. Ortiz measure? __ players
Answer:
Ms. Ortiz measured 9 players.
Explanation:
Line plots like the one above help us organize and display data. Each X in this line plot represents one basketball player. The data height is in the form of inches. In the above image we can observe basket players and their height. Ms. Ortiz measured nine players.
Question 6.
Which height occurs most often? __ inches
Answer:
The height occurs most often is 59 inches.
Explanation:
Line plots like the one above help us organize and display data. Each X in this line plot represents one basketball player. The data height is in the form of inches. In the above image we can observe basket players and their height. The height occurs most often is 59 inches.
Practice
Question 7.
33 + 6 = __
Answer:
33 + 6 = 39
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 33 and 6. First add three and six in one’s place right side then we got nine. Keep nine in one’s place and then add zero to three in ten’s place, left side then we got three write three in ten’s place. By adding these two numbers 33 and 6 we got 39.
Question 8.
__ = 65 + 2
Answer:
67 = 65 + 2
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 65 and 2. First add five and two in one’s place right side then we got seven. Keep seven in one’s place and then add zero to six in ten’s place, left side then we got six write six in ten’s place. By adding these two numbers 65 and 2 we got 67.
Question 9.
__ + 3 = 22
Answer:
19 + 3 = 22
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 19 and 3. First add nine and three in one’s place right side then we got twelve. Keep two in one’s place and then add one to one in ten’s place, left side then we got two write two in ten’s place. By adding these two numbers 19 and 3 we got 22.
Question 10.
9 + 52 = __
Answer:
9 + 52 = 61
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 9 and 52. First add nine and two in one’s place right side then we got eleven. Keep one in one’s place and then add one to five in ten’s place, left side then we got six write six in ten’s place. By adding these two numbers 9 and 52 we got 61.
Everyday Math Grade 2 Home Link 7.9 Answer Key
Vegetable Picture Graph
Family Note
Today your child drew a picture graph, which uses pictures or symbols to show data. The key on a picture graph tells what each picture is for. Have your child use the data table to draw the graph.
Please return this Home Link to school tomorrow.
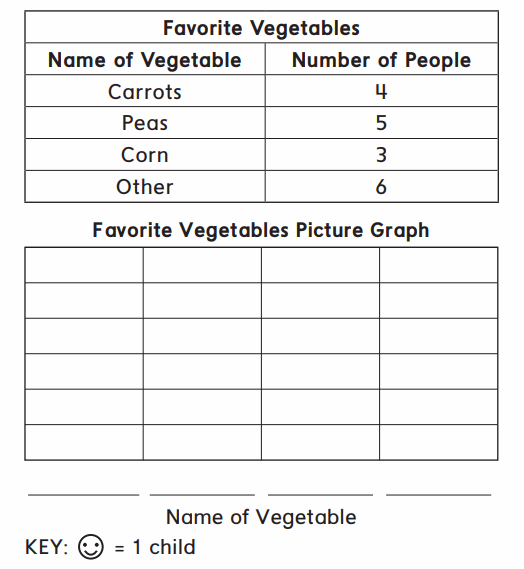
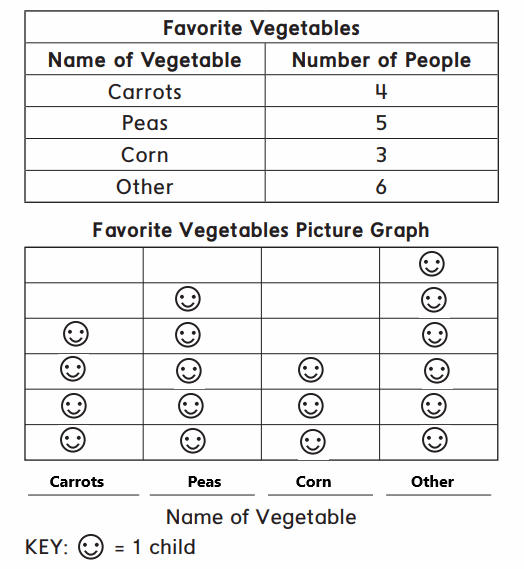
Answer:
Explanation:
In the above image we can observe favorite vegetables with name of vegetable and number of people. In favorite vegetables picture graph one smiley represents one child. Four people like Carrots and five people like peas, three people like corn and other vegetables like six people.
Practice
Question 1.
__ = 21 + 5
Answer:
26 = 21 + 5
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 21 and 5. First add one and five in one’s place right side then we got six. Keep six in one’s place and then add zero to two in ten’s place, left side then we got two write two in ten’s place. By adding these two numbers 21 and 5 we got 26.
Question 2.
63 + 4 = __
Answer:
63 + 4 = 67
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 63 and 4. First add three and four in one’s place right side then we got seven. Keep seven in one’s place and then add zero to six in ten’s place, left side then we got six write six in ten’s place. By adding these two numbers 63 and 4 we got 67.
Question 3.
__ + 88 = 90
Answer:
2 + 88 = 90
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 2 and 88. First add two and eight in one’s place right side then we got ten. Keep zero in one’s place and then add one to eight in ten’s place, left side then we got nine write nine in ten’s place. By adding these two numbers 2 and 88 we got 90.
Question 4.
7 + 35 = __
Answer:
7 + 35 = 42
Explanation:
An addition sentence is a mathematical expression that shows two or more values added together. In the above expression we can observe two numbers 7 and 35. First add seven and five in one’s place right side then we got twelve. Keep two in one’s place and then add one to three in ten’s place, left side then we got four write four in ten’s place. By adding these two numbers 7 and 35 we got 42.