Everyday Mathematics 2nd Grade Answer Key Unit 6 Whole Number Operations and Number Stories
Everyday Math Grade 2 Home Link 6.1 Answer Key
Making a Bar Graph
Family Note
Your child is exploring different ways to display data. One way to display data is in a bar graph. For the activity below, your child may have to ask a neighbor or call a relative to gather the needed pockets data.
Please return this Home Link to school tomorrow.
Question 1.
Pick four people. Count the number of pockets on the clothes that each person is wearing. Record your data in the table.
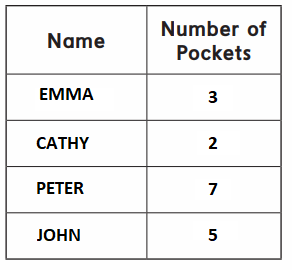
Answer:
Question 2.
Draw a bar graph for your data. First write each person’s name on a line under the graph. Then color the bar above each name to show the number of pockets that each person has.

Answer:
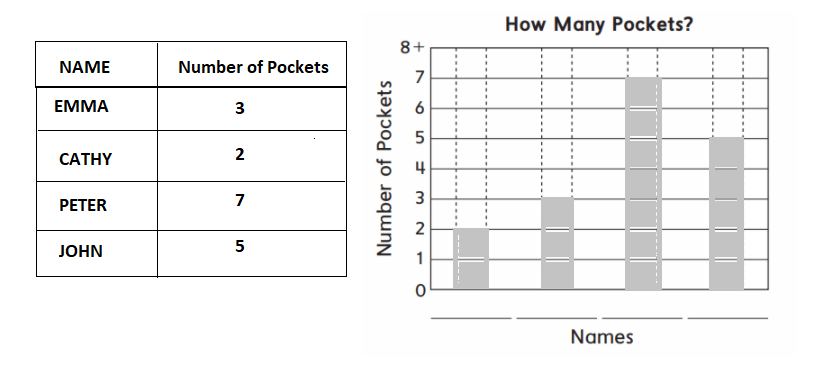
Explanation:
Emma has 3 pockets
Cathy has 2 pockets
Peter has 7 pockets
John has 5 pockets
Everyday Math Grade 2 Home Link 6.2 Answer Key
Comparison Number Stories
For each number story, follow these steps:
- Write the numbers you know in the comparison diagram. Use ? for the number you need to find.
- Write a number model. Use ? for the number you don’t know.
- Solve the problem and answer the question.
Question 1.
Rosa has $29. Omeida has $10. Who has more money? __ How much more?
Number model:
Rosa has $ __ more than Omeida.
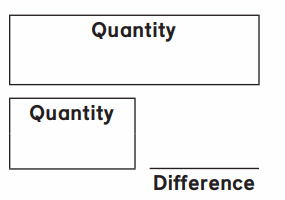
Answer:
Rosa has $19 more then Omeida

Explanation:
Roas has : $29
Omeida has : $10
Difference : $29 – $10 = $19
Rosa has $19 more then Omeida
Question 2.
Omar ran 15 miles. Omar ran 8 more miles than Anthony. How many miles did Anthony run?
Number model:
Anthony ran miles.
Answer:
Anthony ran 7miles
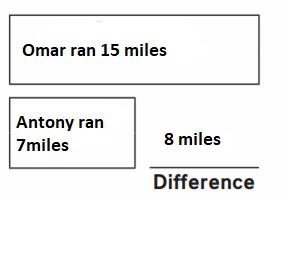
Explanation :
Omar ran 15 miles
Omar ran 8 more miles that means:
Anthony ran 15- 8 = 7miles
Everyday Math Grade 2 Home Link 6.3 Answer Key
Addition and Subtraction Number Stories
Family Note
In today’s lesson your child used diagrams to help solve addition and subtraction number stories. Diagrams help children organize the information from number stories, identify the missing information, and decide whether to add or subtract to solve the problem. Organizing information in a diagram also helps children write a number model using ? to represent what they don’t know.
Encourage your child to choose a diagram that best matches the way he or she sees the problem. There’s no right or wrong diagram for a problem. What matters is that it matches the child’s thinking.
Please return this Home Link to school tomorrow.
Do the following for each number story:
• Write a number model. Use ? to show what you need to find. To help, you may draw a
• Solve the problem and write the answer.
Question 1.
It snowed 16 inches in Chicago on Friday night. It snowed 7 inches on Saturday night. How much snow did Chicago receive in all?
Number model: __
Answer: __ inches
Answer:
Chicago receive 23 inches in all
Explanation :
No. of inches snowed on Friday night : 16 inches
No. of inches snowed on Saturday night : 7 inches
Total snow received by Chicago : 16 + 7 = 23 inches
Question 2.
Evelyn has 30 blocks. She used 24 blocks to build a tower.
How many blocks are not used for the tower?
Number model: __
Answer:
Evelyn has not use 6 blocks in building the tower.
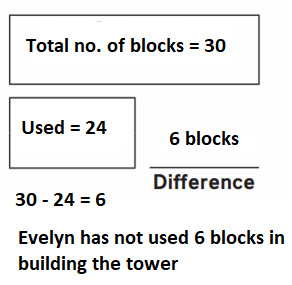
Explanation :
Total no. of blocks Evelyn has : 30
No. of blocks she used in building a tower : 24
No. of blocks not used in building the tower : Total no. of blocks – No. of blocks used in building the tower
: 30 – 24
: 6 blocks
Evelyn has not use 6 blocks in building the tower.
Everyday Math Grade 2 Home Link 6.4 Answer Key
Solving Problems
Family Note
In class today your child solved addition and subtraction number stories involving the heights and lengths of various animals. Some children used mental strategies to solve the stories. Others used tools such as base-10 blocks or open number lines. Others drew pictures or situation diagrams to help organize the information from the stories. Please do not teach your child a formal method, such as the addition method shown at the right. At this stage it is important for children to work with more concrete representations. Children will be introduced to a formal method for addition in Lessons 6-7 and 6-8.
Please return this Home Link to school tomorrow.
Solve the problems below. You may use base-10 shorthand, open number lines, or any other tool except a calculator to help. You may also draw pictures or diagrams.
Question 1.
How tall are the ostrich and polar bear together?
Together they are ___ feet tall.
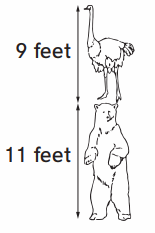
Answer:
20 feet
Explanation :
Height of the bear : 11 feet
Height of the ostrich : 9 feet
Height of ostrich and bear together = Height of the bear + Height of the ostrich
: = 11 + 9
: = 20 feet
Height of ostrich and bear together = 20 feet
Question 2.
How much longer is the giant squid than the crocodile?
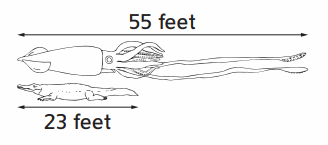
The giant squid is ___ feet longer than the crocodile.
Talk to someone about how you solved each problem.
Answer:
The giant squid is 32 feet longer than the crocodile.
Explanation :
Length of the squid : 55 feet
Length of the crocodile : 23 feet
If we subtract the length of the crocodile from the length of the giant squid we will get
55 – 23 = 32 feet
so,
The giant squid is 32 feet longer than the crocodile.
Everyday Math Grade 2 Home Link 6.5 Answer Key
Two-Step Number Stories
Family Note
In today’s lesson your child solved two-step number stories, which can be broken into two parts and then solved in two steps. For example: Jonathan had 6 tickets for rides at the fair. His mother gave him 9 more. Then he gave 5 tickets to his friend. How many tickets does he have now?
To break this story into two parts, ask: What do you know from the story? (Jonathan had 6 tickets.)
What happened first? (He received 9 more tickets.) What happened next? (He gave away 5 tickets.)
What do you need to find out? (The number of tickets Jonathan has now.)
The first step is to figure out how many tickets Jonathan had after receiving some from his mother. The second step is to figure out how many tickets he had after giving some to his friend. Children are encouraged to solve two-step number stories using a variety of tools: drawings, open number lines, number grids, manipulatives, and diagrams. They also learned to record either one or two number models for each number story—one for each part of the story or one number model to represent the whole story.
For example: Use one number model, such as 6 + 9 – 5 = ?, for both parts. Or, use two number models, such as 6 + 9 = ? and 15 – 5 = ?, one for the first part and one for the second part. Answer: Jonathan now has 10 tickets. Ask your child to explain the steps he or she takes to solve the problem below.
Discuss how his or her number model(s) relates to the number story.
Please return this Home Link to school tomorrow.
• Write a number model or number models. Use ? to show the number you need to find. To help, you may draw a
• Solve the problem and write the answer.
Question 1.
At the beach, 11 children were playing in the sand. Then 6 more children joined them. Then 8 decided to go swimming. How many children were still playing in the sand?
Number model(s): ___
Answer: __ children
Answer:
9 children were still playing in the sand
Explanation :
Children already playing in the sand : 11
Children joined them : 6
Total children playing in the sand : 11 + 6 = 17
Children decided to go swimming : 8
Children were still playing in the sand : Total children playing in the sand – Children decided to go swimming
: : 17 – 8 = 9
9 children were still playing in the sand
Everyday Math Grade 2 Home Link 6.6 Answer Key
Addition Strategies
For each problem:
- Make a ballpark estimate.
- Solve the problem using any strategy you choose. Use words or pictures to show your thinking.
- Check to make sure your answer makes sense.
Question 1.
34 + 59 = ?
Ballpark estimate:
30 + 60 = 90
Strategy:
Combining tens and ones
Answer:
34 + 59 = 93
Explanation :
34 + 59 = ?
Nearest number to 34 is 30 and nearest number to 59 is 60
So ballpark estimate is 30 + 60 = 90
By using the 10’s and ‘s strategy
N30 +4] + [50 + 9]
Now add the tens and ones
30 + 50 = 80
4 + 9 = 13
34 + 59 = 80 + 13 = 93
Question 2.
17 + 68 = ?
Ballpark estimate:
20 + 70 = 90
Strategy:
Open line strategy
Answer :
17 + 68 = 85
Explanation:
The nearest number to 17 is 20
The nearest number to 68 is 70
So the ballpark will be 20 + 70 = 90
By using open line strategy we can calculate 17 + 68
First we have to add 10 to 68
68 + 10 = 78
And then we have to add 7 to 78
78 + 7 = 85

So we get,
17 + 68 = 85
Choose one of the problems above. Explain your estimate to someone at home. Then explain how you checked to make sure your answer made sense.
Answer :
(As in Question 1)
Explanation :
34 + 59 = ?
Nearest number to 34 is 30 and nearest number to 59 is 60
So, I knew that the ballpark estimate is 30 + 60 = 90
By using the 10’s and ‘s strategy i know
[30 +4] + [50 + 9]
I have add the tens and ones
30 + 50 = 80
4 + 9 = 13
34 + 59 = 80 + 13 = 93
I checked my answer using the calculator as 34 + 59 = 93
So I know that my answer is correct
Practice
Complete each number sentence to show the expanded form.
Question 3.
__ = 200 + 40 + 6
Answer:
200 + 40 + 6 = 246
Explanation:
By adding the hundreds, tens and the unit digits we get :
200 + 40 = 240
240 + 6 = 246
So,
200 + 40 + 6 = 246
Question 4.
278 = __+ __ + __
Answer:
200 + 70 + 8 = 278
Explanation:
By splitting the hundreds, tens and the unit digits we get :
200 + 70 + 8 = 278
Question 5.
300 + 50 = __
Answer:
300 + 50 = 350
Explanation:
By adding the hundreds and tens digits we get :
300 + 50 = 350
So,
300 + 50 = 350
Question 6.
420 = __ + __
Answer:
420 = 400 + 20
Explanation:
By splitting the hundreds and tens digits we get :
420 = 400 + 20
Everyday Math Grade 2 Home Link 6.7 Answer Key
Adding with Base-10 Blocks
Family Note
Today children used base-10 blocks to help them add numbers. Three types of base-10 blocks were used: A cube represents 1. A long (a rod that is 10 cubes long) represents 10. A flat (a square that is 10 cubes long and 10 cubes wide) represents 100.
To solve 24 + 32 with base-10 blocks, children first represent each number with blocks or base-10 shorthand:
Then children combine the blocks according to type (longs with longs; cubes with cubes) and count each type of block: 5 longs show 5 tens, or 50; 6 cubes show 6 ones, or 6. The 50 and the 6 are called partial sums because they are parts of the final sum. Finally, children add the partial sums to find the total: 50 + 6 = 56.
Children also use base-10 blocks to add 3-digit numbers by adding the 100s, 10s, and 1s separately and then combining the partial sums to find the total.
Please return this Home Link to school tomorrow.
Use base-10 shorthand to show each number. Then write the partial sums and find the total sum.
Question 1.
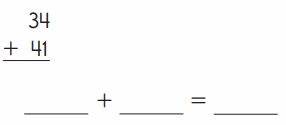
Answer :
34 + 41 = 75
Explanation :
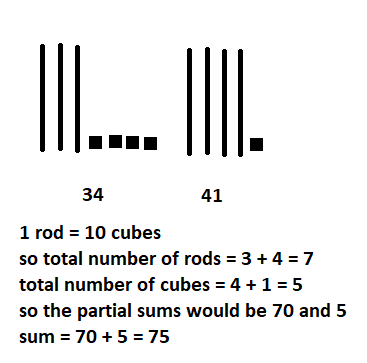
1 rod = 10 cubes
So total number of rods = 3 + 4 = 7
Total number of cubes = 4 + 1 = 5
Partial sums are 70 and 5
Sum = 70 + 5 = 75
Question 2.
Answer:
27 + 25 = 52
Explanation :
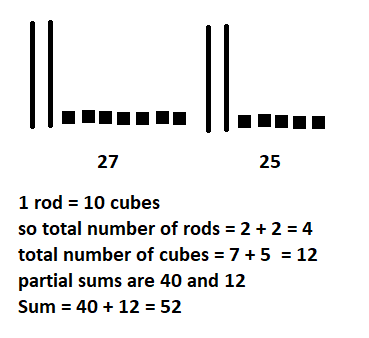
1 rod = 10 cubes
So total number of rods = 2 + 2 = 4
Total number of cubes = 7 + 5 = 12
Partial sums are 40 and 12
Sum = 40 + 12 = 52
Explain to someone at home how you use base-10 blocks to add.
Practice
Complete each number sentence to show the expanded form of a number.
Question 3.
__ = 500 + 30 + 2
Answer:
500 + 30 + 2 = 532
Explanation :
By adding the hundreds, tens and the unit digits we get :
500 + 30 = 530
530 + 2 = 532
So,
500 + 30 + 2 = 532
Question 4.
340 = __ + __
Answer:
340 = 300 + 40
Explanation :
By splitting the number we get the 2 partial sums
300 and 40
So
340 = 300 + 40
Question 5.
400 + 5 = __
Answer:
400 + 5 = 405
Explanation :
By adding the 2 partial sums we get :
400 + 5 = 405
Question 6.
609 = __ + __
Answer:
609 = 600 + 9
Explanation :
By splitting the number into its partial sums we get
609 = 600 + 9
Everyday Math Grade 2 Home Link 6.8 Answer Key
More Partial Sums
Family Note
In the previous lesson your child used base-10 blocks to help find partial sums. Today your child used expanded form. Expanded form shows numbers broken apart into a sum of place-value pieces, such as hundreds, tens, and ones. For example, the expanded form for 324 is 300 + 20 + 4.
To solve 324 + 255, your child can first write or think about each number in expanded form, then use the expanded form to help find the partial sums:
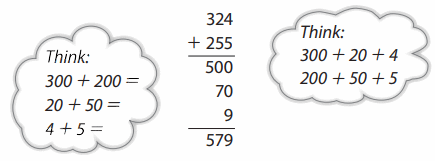
Encourage your child to use place-value language when working with this method. For example, when adding the 100s in this example, guide your child to say “300 + 200 = 500,” not “3 + 2 = 5.” Writing the expanded form can help children remember to use the correct language.
This method of finding partial sums and then combining the partial sums to find the total is called partial-sums addition. Partial-sums addition was introduced only recently, so allow plenty of time for practice before expecting your child to use it easily.
Please return this Home Link to school tomorrow.
Fill in the unit box. For each problem:
- Make a ballpark estimate. Solve the problem using partial-sums addition. Show your work.
- Use your ballpark estimate to check if your answer makes sense.
Question 1.
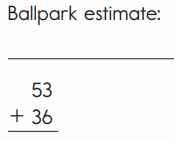
Answer:
Ballpark Estimate :
50 + 30 = 80
Answer : 53 + 36 = 89
Explanation :
According To Ballpark Estimate :
50 + 30 = 80
Add the tens digits:
50 + 30 = 80
Now add the units digits :
3 + 6 = 9
Now add them together
80 + 9 = 89
53 + 36 = 89
Question 2.
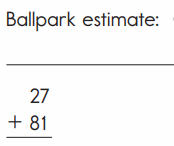
Answer:
According To Ballpark Estimate :
30 + 80 = 110
Answer :
27 + 81 = 108
Explanation :
Ballpark Estimate : 30 + 80 = 110
Add the 10s digits
20 + 80 = 100
7 + 1 = 8
100 + 8 = 108 so we get
27 + 81 = 108
Question 3.
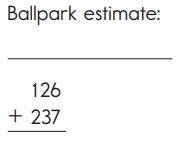
Answer:
Ballpark estimate :
Answer :
125 + 240 = 365
Explanation :
Ballpark estimate : 125 + 240 = 365
Now add the hundreds
100 + 200 = 300
Now add the tens
20 + 30 = 50
Now add the ones
6 + 7 = 13
Now add the hundreds, tens and ones
300 + 50 + 13 = 363
So we get,
126 + 237 = 363
Everyday Math Grade 2 Home Link 6.9 Answer Key
Subtraction Number Stories
Family Note
In today’s lesson, your child solved subtraction number stories using different tools and strategies based on place-value concepts and explained his or her thinking in drawings and words. Being able to solve problems in multiple ways and explain their strategies helps children become flexible problem solvers.
As your child solves these problems, ask him or her to explain the strategy.
Please return this Home Link to school tomorrow.
Question 1.
Sam is on a baseball team. This year he set a goal of scoring 36 runs for his team. So far Sam has scored 26 runs. How many more runs does Sam need to score in order to meet his goal?
__ runs
Answer:
10 runs
Explanation :
Total runs to be scored : 36
Runs Sam scored : 26
Runs need for Sam to reach is goal : 36 – 26 = 10 runs
10 runs need more to score to meet his goal
Question 2.
Sam helped his mother unload the dishwasher. As he was putting the silverware away, Sam counted 21 spoons and 13 forks. How many more spoons than forks did Sam unload?
__ spoons
Answer:
8 spoons
No. of spoons : 21 spoons
No. of forks : 13 forks
21 – 13 = 8
8 spoons more then forks
Practice
Question 3.
a. 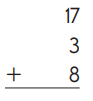
Answer:
28
Explanation :
17 + 3 + 8 = 28
b. 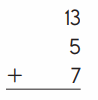
Answer:
25
Explanation :
13 + 5 + 7 = 25
c. 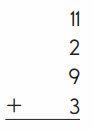
Answer:
25
Explanation :
11 + 2 + 9 + 3 = 25
d. 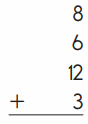
Answer:
29
Explanation :
8 + 6 + 12 + 3 = 29
Everyday Math Grade 2 Home Link 6.10 Answer Key
How Many?
Family Note
Your child has been working with arrays to develop readiness for multiplication. Arrays are rectangular arrangements of objects that have the same number of objects in each row. For example, a 3-by-5 array is shown at the right.
Your child found the total number of objects in each array and learned to write addition number models to represent arrays. One example of an addition number model for this array is 5 + 5 + 5 = 15. There are 15 Xs in all.
When your child writes an addition number model to show the number of objects in a 5-by-4 array, he or she is building understanding of the meaning of four 5s, or 4 × 5.
Please return this Home Link to school tomorrow.
Question 1.
Draw an array with 2 rows of Xs with 8 Xs in each row.
Write an addition number model for the array.
Answer:
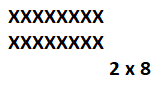
Number model :
8 + 8 = 16
Question 2.
Draw an array with 4 rows of Xs with 6 Xs in each row.
Write an addition number model for the array.
Answer:
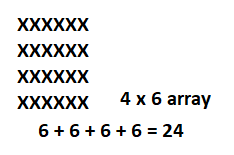
Number model :
6 + 6 + 6 + 6 = 24
Question 3.
Draw an array with 3 rows of Xs with 7 Xs in each row.
Write an addition number model for the array.
Answer:
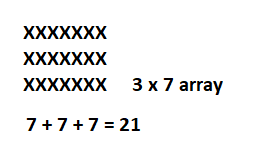
Number model :
7 + 7 + 7 = 21