Engage NY Eureka Math Precalculus Module 5 Lesson 2 Answer Key
Eureka Math Precalculus Module 5 Lesson 2 Exercise Answer Key
Example 1: Fundamental Counting Principle
A restaurant offers a fixed-price dinner menu for $30. The dinner consists of three courses, and the diner chooses one item for each course.
The menu is shown below:
First Course
Salad
Tomato Soup
French Onion Soup
Second Course
Burger
Grilled Shrimp
Mushroom Risotto
Ravioli
Third Course
Cheesecake
Ice Cream Sundae
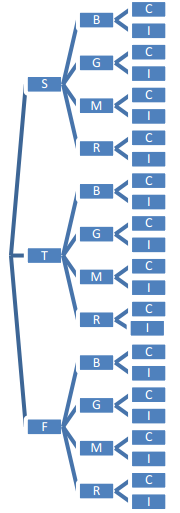
Exercises 1–4
Exercise 1.
Make a list of all of the different dinner fixed-price meals that are possible. How many different meals are possible?
Answer:
Note: The list below shows all the possibilities using abbreviations of the items.
They are listed in order: first course choice, second course choice, and third course choice. For example, SBC would represent salad, burger, and cheesecake.
There are 24 different dinner fixed-price meals possible.
SBC TBC FBC
SBI TBI FBI
SGC TGC FGC
SGI TGI FGI
SMC TMC FMC
SMI TMI FMI
SRC TRC FRC
SRI TRI FRI
Exercise 2.
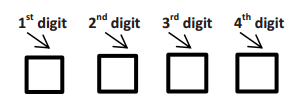
For many computer tablets, the owner can set a 4-digit pass code to lock the device.
a. How many digits could you choose from for the first number of the pass code?
Answer:
10
b. How many digits could you choose from for the second number of the pass code? Assume that the numbers can be repeated.
Answer:
10
c. How many different 4-digit pass codes are possible? Explain how you got your answer.
Answer:
10 ∙ 10 ∙ 10 ∙ 10 = 10000
There are 10 choices for the first digit, 10 choices for the second digit, 10 choices for the third digit, and 10 choices for the fourth digit. I used the fundamental counting principle and multiplied the number of choices for each digit together to get the number of possible pass codes.
d. How long (in hours) would it take someone to try every possible code if it takes three seconds to enter each possible code?
Answer:
It would take 30,000 seconds, which is 8 1/3 hr.
Exercise 3.
The store at your school wants to stock sweatshirts that come in four sizes (small, medium, large, xlarge) and in two colors (red and white). How many different types of sweatshirts will the store have to stock?
Answer:
4 ∙ 2 = 8
Exercise 4.
The call letters for all radio stations in the United States start with either a W (east of the Mississippi River) or a K (west of the Mississippi River) followed by three other letters that can be repeated. How many different call letters are possible?
Answer:
2 ∙ 26 ∙ 26 ∙ 26 = 35152
Example 2: Permutations
Suppose that the 4-digit pass code a computer tablet owner uses to lock the device cannot have any digits that repeat. For example, 1234 is a valid pass code. However, 1123 is not a valid pass code since the digit 1 is repeated.
An arrangement of four digits with no repeats is an example of a permutation. A permutation is an arrangement in a certain order (a sequence).
How many different 4-digit pass codes are possible if digits cannot be repeated?
Exercises 5–9
Exercise 5.
Suppose a password requires three distinct letters. Find the number of permutations for the three letters in the code if the letters may not be repeated.
Answer:
26P3 = 26 ∙ 25 ∙ 24 = 15600
Exercise 6.
The high school track has 8 lanes. In the 100-meter dash, there is a runner in each lane. Find the number of ways that 3 out of the 8 runners can finish first, second, and third.
8P3 = 8 ∙ 7 ∙ 6 = 336
Exercise 7.
There are 12 singers auditioning for the school musical. In how many ways can the director choose first a lead singer and then a stand-in for the lead singer?
Answer:
12P2 = 12 ∙ 11 = 132
Exercise 8.
A home security system has a pad with 9 digits (1 to 9). Find the number of possible 5-digit pass codes:
a. If digits can be repeated.
Answer:
9 ∙ 9 ∙ 9 ∙ 9 ∙ 9 = 59049
b. If digits cannot be repeated.
Answer:
9P5 = 9 ∙ 8 ∙ 7 ∙ 6 ∙ 5 = 15120
Exercise 9.
Based on the patterns observed in Exercises 5–8, describe a general formula that can be used to find the number of permutations of n things taken r at a time, or nPr.
Answer:
Based on the answers to the exercises, a permutation of n things taken r at a time can be found using the formula:
n ∙ (n-1) ∙ (n-2) ∙ … ∙ (n-r+1).
Exercises 10–15
Exercise 10.
If 9! is 362,880, find 10!.
Answer:
3,628,800
Exercise 11.
How many different ways can the 16 numbered pool balls be placed in a line on the pool table?
Answer:
16! or 16P16 ≈ 2 ∙ 1013
Exercise 12.
Ms. Smith keeps eight different cookbooks on a shelf in one of her kitchen cabinets. How many ways can the eight cookbooks be arranged on the shelf?
Answer:
8! or 8P8 = 40320
Exercise 13.
How many distinct 4-letter groupings can be made with the letters from the word champion if letters may not be repeated?
Answer:
8P4 = \(\frac{8 !}{(8-4) !}\) = 1680
Exercise 12.
There are 12 different rides at an amusement park. You buy five tickets that allow you to ride on five different rides. In how many different orders can you ride the five rides? How would your answer change if you could repeat a ride?
Answer:
Different order: 12P5 = \(\frac{12 !}{(12-5) !}\)! = 95040
Repeat rides: 125 = 248 832
Exercise 13.
In the summer Olympics, 12 divers advance to the finals of the 3-meter springboard diving event. How many different ways can the divers finish 1st, 2nd, or 3rd?
Answer:
12P3 = \(\frac{12 !}{(12-3) !}\) = 1320
Eureka Math Precalculus Module 5 Lesson 2 Problem Set Answer Key
Question 1.
For each of the following, show the substitution in the permutation formula, and find the answer.
a. 4P3
Answer:
\(\frac{4 !}{(4-4) !}\) = \(\frac{4 \cdot 3 \cdot 2 \cdot 1}{0 !}\) = 24
b. 10P2
Answer:
\(\frac{10 !}{(10-2) !}\) = \(\frac{10 !}{8 !}\) = 10 ∙ 9 = 90
c. 5P1
\(\frac{5 !}{(5-1) !}\) = \(\frac{5 !}{4 !}\) = 5
Question 2.
A serial number for a TV begins with three letters, is followed by six numbers, and ends in one letter. How many different serial numbers are possible? Assume the letters and numbers can be repeated.
Answer:
26 ∙ 26 ∙ 26 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 26 ≈ 4.6 ∙ 1011
Question 3.
In a particular area code, how many phone numbers (###-####) are possible? The first digit cannot be a zero, and assume digits can be repeated.
Answer:
9 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 = 9 000 000
Question 4.
There are four teams in the AFC East division of the National Football League: Bills, Jets, Dolphins, and Patriots. How many different ways can two of the teams finish first and second?
Answer:
4P<sub2 = 12
Question 5.
How many ways can 3 of 10 students come in first, second, and third place in a spelling contest if there are no ties?
Answer:
10P3 = 720
Question 6.
In how many ways can a president, a treasurer, and a secretary be chosen from among nine candidates if no person can hold more than one position?
Answer:
9P3 = 504
Question 7.
How many different ways can a class of 22 second graders line up to go to lunch?
Answer:
22! = 22P22 ≈ 1.1 ∙ 1021
Question 8.
Describe a situation that could be modeled by using 5P2.
Answer:
Answers will vary. Suppose that there are five members of a family living at home. The first one home has to take out the garbage, and the second one home has to walk the dog. 5P2 can be used to model the number of ways the family members can be assigned the different tasks.
Question 9.
To order books from an online site, the buyer must open an account. The buyer needs a username and a password.
a. If the username needs to be eight letters, how many different usernames are possible:
i. If the letters can be repeated?
Answer:
268 ≈ 2 ∙ 1011
ii. If the letters cannot be repeated?
Answer:
26P8 ≈ 6.3 ∙ 1010
b. If the password must be eight characters, which can be any of the 26 letters, 10 digits, and 12 special keyboard characters, how many passwords are possible:
i. If characters can be repeated?
Answer:
488 ≈ 2.8 ∙ 1013
ii. If characters cannot be repeated?
Answer:
48P 8 ≈ 1.5 ∙ 1013
c. How would your answers to part (b) change if the password is case-sensitive? (In other words, Password and password are considered different because the letter p is in uppercase and lowercase.)
Answer:
The answers would change because the number of letters that can be used will double to 52, which means the number of characters that can be used is now 74.
So, if characters can be repeated, the answer will be 728 ≈ 7.2 ∙ 1014.
If characters cannot be repeated, the answer will be 72P8 ≈ 4.8 ∙ 1014.
Question 10.
Create a scenario to explain why 3P3 = 3!.
Answer:
Suppose three friends are running in a race. 3P3 can be used to model the order in which the three friends finish in 1st, 2nd, and 3rd place. There are three choices for 1st place and two choices for 2nd place, which only leaves one choice for 3rd place. So, there are 3 ∙ 2 ∙ 1 ways for the friends to finish the race, which is the same as 3! or 6.
Question 11.
Explain why nPn = n! for all positive integers n.
Answer:
Using the permutation formula:
nPr = \(\frac{\boldsymbol{n} !}{(\boldsymbol{n}-\boldsymbol{r}) !}\)
In this case, r = n; therefore:
nPn = \(\frac{n !}{(n-n) !}\) = \(\frac{n !}{0 !}\) = \(\frac{n !}{1 !}\) = n!.
Eureka Math Precalculus Module 5 Lesson 2 Exit Ticket Answer Key
Question 1.
The combination for the lock shown below consists of three numbers.

a. If the numbers can be repeated, how many different combinations are there? Explain your answer.
Answer:
403 = 64000
Because numbers can be repeated, there are 40 choices for each of the three digits. Therefore, I applied the fundamental counting principle.
b. If the numbers cannot be repeated, how many different combinations are there? Explain your answer.
Answer:
40P3 = 59280
Since numbers cannot be repeated, this is an example of a permutation.
Question 2.
Jacqui is putting together sets of greeting cards for a school fundraiser. There are four different card options, two different colored envelopes, and four different sticker designs. A greeting card set consists of one type of card, one color for the envelopes, and one sticker design. How many different ways can Jacqui arrange the greeting card sets? Explain how you determined your answer.
Answer:
4 ∙ 2 ∙ 4 = 32
By using the fundamental counting principle, there are 32 ways to arrange the sets.