Eureka Math Precalculus Module 5 Lesson 17 Answer Key

Engage NY Eureka Math Precalculus Module 5 Lesson 17 Answer Key

Eureka Math Precalculus Module 5 Lesson 17 Exercise Answer Key

Exercises 1–5
Exercise 1.
What are the possible total amounts of money you could win if you scratch off two disks?
Answer:
If two $1.00 disks are uncovered, the total is $2.00. If one $1.00 disk and the $10.00 disk are uncovered, the total is $11.00.

Exercise 2.
If you pick two disks at random:
a. How likely is it that you win $2.00?
Answer:
P(win $2.00) = \(\frac{10}{15}\) = \(\frac{2}{3}\)

b. How likely is it that you win $11.00?
Answer:
P(win $11.00) = \(\frac{5}{15}\) = \(\frac{1}{3}\)
Following are two methods to determine the probabilities of getting $2.00 and $11.00.

Method 1:
List the possible pairs of scratched disks in a sample space, S, keeping in mind that two different disks need to be scratched, and the order of choosing them does not matter. For example, you could use the notation AB that indicates disk A and disk B were chosen, in either order.
S = {AB, AC, AD, AE, AF, BC, BD, BE, BF, CD, CE, CF, DE, DF, EF}
There are 15 different ways of choosing two disks without replacement and without regard to order from the six possible disks.
Identify the winning amount for each choice under the outcome in S. Suppose that disks A–E hide $1.00, and disk F hides $10.00.

Since each of the outcomes in S is equally likely, the probability of winning $2.00 is the number of ways of winning $2.00, namely, 10, out of the total number of possible outcomes, 15. P(win $2.00) = \(\frac{10}{15}\) = \(\frac{2}{3}\). Similarly, P(win $11.00) = \(\frac{5}{15}\) = \(\frac{1}{3}\).

Method 2:
Previous lessons studied permutations and combinations. Recall that counting when sampling was done without replacement and without regard to order involved combinations.
The number of ways of choosing two disks without replacement and without regard to order is
₆C₂ = \(\frac{6(5)}{2}\) = 15. _nC_k denotes the number of combinations of n items taken k at a time without replacement and without regard to order.)
To win $2.00, two disks need to be chosen from the five $1.00 disks. The number of ways of doing that is
₅C₂ = \(\frac{5(4)}{2}\) = 10.
So, the probability of winning $2.00 is 10/15 = \(\frac{2}{3}\).
To win $11.00, one disk needs to be chosen from the five $1.00 disks, and the $10.00 disk needs to be chosen. The number of ways of doing that is (₅C₁)(₁C₁) = 5(1) = 5. So, the probability of winning $11.00 is \(\frac{5}{15}\) = \(\frac{1}{3}\).

Exer’ 3.
Based on Exercise 2, how much should you expect to win on average per game if you played this game a large number of times?
Answer:
(2)(\(\frac{2}{3}\)) + (11)(\(\frac{1}{3}\)) = 5.00 The expected winning amount per play is $5.00.

Exercise 4.
To play the game, you must purchase a game card. The price of the card is set so that the game is fair. What do you think is meant by a fair game in the context of playing this instant lottery game?
Answer:
Responses from students concerning what they think is meant by a fair game will no doubt vary. For example, the cost to play the game should be equal to the expected winnings.

Exercise 5.
How much should you be willing to pay for a game card if the game is to be a fair one? Explain.
Answer:
Responses will vary. In the context of this instant lottery game, the game is fair if the player is willing to pay $5.00 (the expected winning per play) to purchase each game card.

Exercise 6.
Do you think you should take your mom’s original payment of $10.00 or play the “bag” game? In other words, is this game a fair alternative to getting paid $10.00? Use a probability distribution to help answer this question.
Answer:
Suppose that disks (bags) A, B, C hide $2.00 each, disks D and E hide $5.00 each, and disk F hides $20.00.

You could win $4.00, $7.00, $10.00, $22.00, or $25.00.
Since each of the outcomes in S is equally likely, the probability of winning $4.00 is the number of ways of winning $4.00, namely, 3, out of the total number of possible outcomes, 15. P (win $4.00) = \(\frac{3}{15}\). Similarly, P(win $7.00) is equal to the number of ways of winning $7.00 divided by the total number of possible outcomes, namely, P(win $7.00) = \(\frac{6}{15}\).

The probability distribution for the winning amount per play is as follows:

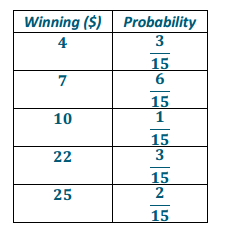
The expected winning amount per play is as follows:
($4)(\(\frac{3}{15}\)) + ($7)(\(\frac{6}{15}\)) + ($10)(\(\frac{1}{15}\)) + ($22)(\(\frac{3}{15}\)) + ($25)(\(\frac{2}{15}\)) = $12.00.
The game is in your favor as its expected winning is $12.00 compared to $10.00, but answers will vary. The key is that students recognize that the expected payment for the game is greater than $10.00 but that on any individual play, they could get less than $10.00. In fact, the probability of getting less than $10.00 is greater than the probability of getting $10.00 or more.

Exercise 7.
Alter the contents of the bag in Example 2 to create a game that would be a fair alternative to getting paid $10.00. You must keep six bills in the bag, but you can choose to include bill – sized pieces of paper that are marked as $0.00 to represent a $0.00 bill.
Answer:
Answers will vary. The easiest answer is to replace all six bills with $5.00 bills. But other combinations are possible, such as three $0.00 bills and three $10.00 bills. If students come up with other possibilities, make sure they support their answers with an expected value calculation.

Exercises 8–9
Exercise 8.
Is it worth purchasing the additional year warranty? Why or why not?
Answer:
(0.05)(180) + (0.15)(65) = 18.75
The expected cost of repairs in the second year is $18.75. So, based on expected value, $24.95 is too high.

Exercise 9.
If the cost of the additional year warranty is too high, what would be a fair price to charge?
Answer:
A fair price for the waranty would be $18.75.

Exercises 10–11
Exercise 10.
The math club is trying to decide what to charge to play the game and what the winning payoff should be per play to make it a fair game. Give an example.
Answer:
Answers will vary. If the game is to be fair, the expected amount of money taken in should equal the expected amount of payoff. Let x cents be the amount to play the game and y be the amount won by the player. The math club receives x cents whether or not the player wins. The math club loses y cents if the player wins. So, for the game to be fair, x – y(\(\frac{12}{25}\)) must be 0. Any x and y that satisfy 25x – 12y = 0 are viable. One example is for the math club to charge 12 cents to play each game with a payoff of 25 cents.

Exercise 11.
What should the math club charge per play to make $0.25 on average for each game played? Justify your answer.
Answer:
Answers will vary. For the math club to clear 25 cents on average per game, the expected amount they receive minus the expected amount they pay out needs to equal 25 (i.e., x – y(\(\frac{12}{25}\)) = 25, or 25x – 12y = 625 where x and y are in cents). For example, if the math club charges 100 cents to play, then the player would receive 156.25 cents if she wins, and the club would expect to clear 25 cents per game in the long run.

Eureka Math Precalculus Module 5 Lesson 17 Problem Set Answer Key

Question 1.
A game is played by drawing a single card from a regular deck of playing cards. If you get a black card, you win nothing. If you get a diamond, you win $5.00. If you get a heart, you win $10.00. How much would you be willing to pay if the game is to be fair? Explain.
Answer:
The following represents a probability distribution:

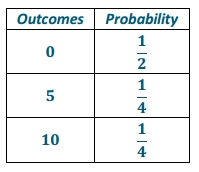
Expected winnings: 0(\(\frac{1}{2}\)) + 5(\(\frac{1}{4}\)) + 10(\(\frac{1}{4}\)) = 3.75. For the game to be fair, the fee should be $3.75.

Question 2.
Suppose that for the game described in Problem 1, you win a bonus for drawing the queen of hearts. How would that change the amount you are willing to pay for the game? Explain.
Answer:
The fee to play the game should increase, as the expected winnings will increase. For example, if a bonus of $10.00 is earned for drawing the queen of hearts, the probability distribution will be

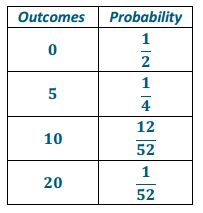
Expected winnings: 0(\(\frac{1}{2}\)) + 5(\(\frac{1}{4}\)) + 10(\(\frac{12}{52}\)) + 20(\(\frac{1}{52}\)) ≈ 3.94. For the game to be fair, the fee should be no more than $3.94, which is an increase from $3.75.

Question 3.
You are trying to decide between playing two different carnival games and want to only play games that are fair.
One game involves throwing a dart at a balloon. It costs $10.00 to play, and if you break the balloon with one throw, you win $75.00. If you do not break the balloon, you win nothing. You estimate that you have about a 15% chance of breaking the balloon.

The other game is a ring toss. For $5.00 you get to toss three rings and try to get them around the neck of a bottle. If you get one ring around a bottle, you win $3.00. For two rings around the bottle, you win $15.00. For three rings, you win $75.00. If no rings land around the neck of the bottle, you win nothing. You estimate that you have about a 15% chance of tossing a ring and it landing around the neck of the bottle. Each toss of the ring is independent.
Which game will you play? Explain.
Answer:
The following are probability distributions for each of the games:

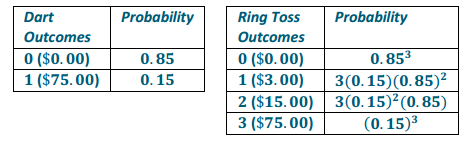
0(0.85) + 75(0.15) = 11.25
The expected winnings for the dart game are $11.25. The dart game is fair because the cost to play is less than the expected winnings.
0∙(0.85)³ + 3∙3(0.15) (0.85)² + 15∙3(0.15)² (0.85) + 75∙(0.15)³ ≈ 2.09
The expected winnings for the ring toss game are approximately $2.09. For the ring toss outcomes of 1 and 2, there is a multiplier of 3 because there are three different ways to get 1 and 2 rings on a bottle in 3 tosses. The ring toss game is not fair because the cost to play is more than the expected winnings.
I would play the dart game.

Question 4.
Invent a fair game that involves three fair number cubes. State how the game is played and how the game is won. Explain how you know the game is fair.
Answer:
Answers will vary. One example is given here.
The key is to determine probabilities correctly. Rolling three fair number cubes results in (6)(6)(6) or 216 possible ordered triples. Two events of interest could be “all same” (i.e., 111, 222, 333, 444, 555, or 666). The probability of “all same” is \(\frac{6}{216}\). Another event could be “all different.” The number of ways of getting “all different” digits is the permutation (6)(5)(4) = 120. Getting any other outcome would have probability 1 – (\(\frac{6}{216}\)) – (\(\frac{120}{216}\)) = \(\frac{90}{216}\).
Consider this game. Roll three fair number cubes. If the result is “all same digit, ” then you win $20.00. If the result is “all different digits, ” you win $1.00. Otherwise, you win $0.00. It costs $1.11 to play.
($20)(\(\frac{6}{216}\)) + ($1)(\(\frac{120}{216}\)) + ($0)(\(\frac{90}{216}\)) ≈ $1.11
The game is approximately fair since the expected winnings per play are approximately $1.11.

Question 5.
Invent a game that is not fair that involves three fair number cubes. State how the game is played and how the game is won. Explain how you know the game is not fair.
Answer:
Answers will vary. One example is given here.
From Problem 4, any fee to play that is not $1.11 results in a game that is not fair. If the fee to play is lower than $1.11, then the game is in the player’s favor. If the fee to play is higher than $1.11, then the game is in the favor of whoever is sponsoring the game.

Eureka Math Precalculus Module 5 Lesson 17 Exit Ticket Answer Key

Question 1.
A game is played with only the four kings and four jacks from a regular deck of playing cards. There are three “one – eyed” cards: the king of diamonds, the jack of hearts, and the jack of spades. Two cards are chosen at random without replacement from the eight cards. Each one – eyed card is worth $2.00, and non – one – eyed cards are worth $0.00. In the following table, JdKs indicates that the two cards chosen were the jack of diamonds and the king of spades. Note that there are 28 pairings. The one – eyed cards are highlighted.

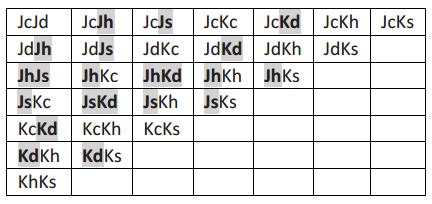
a. What are the possible amounts you could win in this game? Write them in the cells of the table next to the corresponding outcomes.
Answer:

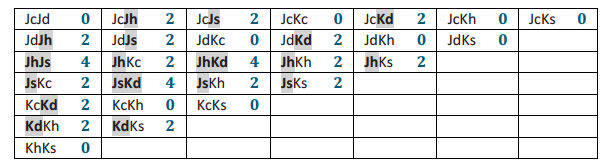
b. Find the the expected winnings per play.
Answer:
Ask students to verify their accumulated counts using combinations. There are 10 pairings where neither card is one – eyed (₅C₂ = 10), 15 pairings with one card one – eyed (₅C₁)(₃C₁) = 15), and 3 pairings in which both cards are one – eyed (₃C₃ = 1).
(0)(\(\frac{10}{28}\)) + (2)(\(\frac{15}{28}\)) + (4)(\(\frac{3}{28}\)) = \(\frac{42}{28}\), or $1.50
The expected winnings per play is $1.50.

c. How much should you be willing to pay per play of this game if it is to be a fair game?
Answer:
According to the expected value of part (b), a player should be willing to pay $1.50 to play the game in order for it to be a fair game.