Eureka Math Precalculus Module 4 Lesson 5 Answer Key

Engage NY Eureka Math Precalculus Module 4 Lesson 5 Answer Key

Eureka Math Precalculus Module 4 Lesson 5 Exercise Answer Key

Exercises 1–12
The circle shown to the right is a unit circle, and the length of \(\widehat{D A}\) is \(\frac{\pi}{3}\) radians.

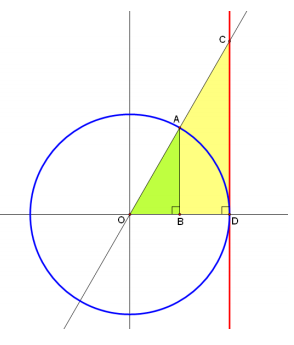
Exercise 1.
Which segment in the diagram has length sin⁡(\(\frac{\pi}{3}\))?
Answer:
The sine of \(\frac{\pi}{3}\) is the vertical component of point A, so \(\overline{A B}\) has length sin(\(\frac{\pi}{3}\)).

Exercise 2.
Which segment in the diagram has length cos⁡(\(\frac{\pi}{3}\))?
Answer:
The cosine of \(\frac{\pi}{3}\) is the horizontal component of point A, so \(\overline{O B}\) has length cos(\(\frac{\pi}{3}\)).

Exercise 3.
Which segment in the diagram has length tan⁡(\(\frac{\pi}{3}\))?
Answer:
Since △OAB is similar to △OCD, \(\frac{C D}{1}\) = \(\frac{A B}{O B}\) = \(\frac{\sin \left(\frac{\pi}{3}\right)}{\cos \left(\frac{\pi}{3}\right)}\). Thus, \(\overline{C D}\) has
length tan(\(\frac{\pi}{3}\)).

Exercise 4.
Which segment in the diagram has length sec⁡(\(\frac{\pi}{3}\))?
Answer:
Since △OAB is similar to △OCD, \(\frac{OD}{OB}\) = \(\frac{OC}{OA}\). Since OA = OD = 1, we have OC = \(\frac{1}{OB}\) = \(\frac{1}{\cos \left(\frac{\pi}{3}\right)}\). Thus, \(\overline{O C}\) has length sec(\(\frac{\pi}{3}\)).

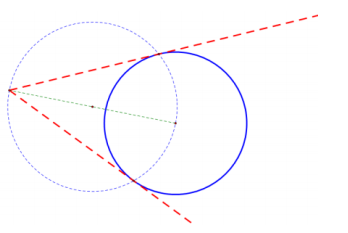
Exercise 5.
Use a compass to construct the tangent lines to the given circle that pass through the given point.

Answer:
Sample solution:

Exercise 6.
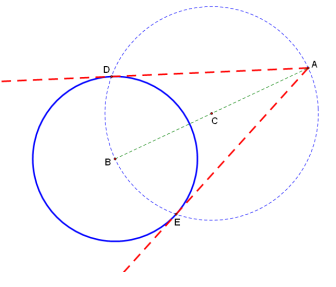
Analyze the construction shown below. Argue that the lines shown are tangent to the circle with center B.

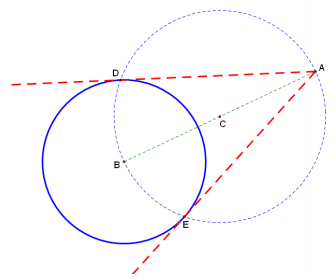
Answer:
Since point D is on circle C, we know that ∠BDA is a right angle. Since point D is on circle B and ∠BDA is a right angle, it follows that (AD) ⃡ is tangent to circle B. In the same way, we can show that \(\overleftrightarrow{A E}\) is tangent to circle B.

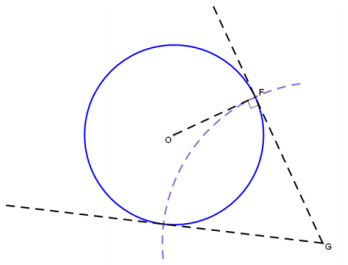
Exercise 7.
Use a compass to construct a line that is tangent to the circle below at point F. Then choose a point G on the tangent line, and construct another tangent to the circle through G.

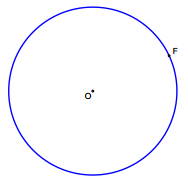
Answer:
Sample solution:

Exercise 8.
The circles shown below are unit circles, and the length of \(\widehat{D A}\) is \(\frac{\pi}{3}\) radians.

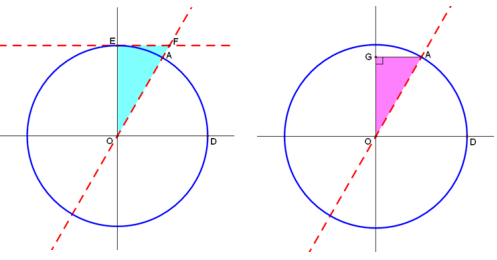
Which trigonometric function corresponds to the length of \(\overline{E F}\)?
Answer:
The length of \(\overline{E F}\) represents the cotangent of \(\frac{\pi}{3}\).

Exercise 9.
Which trigonometric function corresponds to the length of \(\overline{O F}\)?
Answer:
The length of \(\overline{O F}\) represents the cosecant of \(\frac{\pi}{3}\).

Exercise 10.
Which trigonometric identity gives the relationship between the lengths of the sides of △OEF?
Answer:
cot² (\(\frac{\pi}{3}\)) + 1² = csc² (\(\frac{\pi}{3}\))

Exercise 11.
Which trigonometric identities give the relationships between the corresponding sides of △OEF and △OGA?
Answer:
We have \(\frac{1}{\sin \left(\frac{\pi}{3}\right)}\) = \(\frac{\cot \left(\frac{\pi}{3}\right)}{\cos \left(\frac{\pi}{3}\right)}\) and \(\frac{1}{\sin \left(\frac{\pi}{3}\right)}\) = \(\frac{\csc \left(\frac{\pi}{3}\right)}{1}\).

Exercise 12.
What is the value of csc(\(\frac{\pi}{3}\))? What is the value of cot(\(\frac{\pi}{3}\))? Use the Pythagorean theorem to support your answers.
Answer:
Let x = EF. Then we have x² + 1² = (2x)² = 4x², which means 3x² = 1; therefore, x = \(\sqrt{\frac{1}{3}}\). So cot(\(\frac{\pi}{3}\)) = \(\sqrt{\frac{1}{3}}\)
and csc(\(\frac{\pi}{3}\)) = 2\(\sqrt{\frac{1}{3}}\).

Eureka Math Precalculus Module 4 Lesson 5 Problem Set Answer Key

Question 1.
Prove Thales’ theorem: If A, B, and P are points on a circle where (AB) ̅ is a diameter of the circle, then ∠APB is a right angle.
Answer:

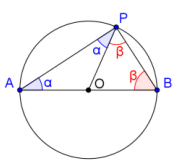
Since OA = OP = OB, △OPA and △OPB are isosceles triangles. Therefore, m∠OAP = m∠OPA, and m∠OPB = m∠OBP.
Let m∠OPA = α and m∠OPB = β. The sum of three internal angles of △APB equals 180°.
Therefore, α + (α + β) + β = 180°, so 2α + 2β = 180°, and α + β = 90°. Since m∠APB = α + β, we have m∠APB = 90°, so ∠APB is a right angle.

Question 2.
Prove the converse of Thales’ theorem: If \(\overline{A B}\) is a diameter of a circle and P is a point so that ∠APB is a right angle, then P lies on the circle for which \(\overline{A B}\) is a diameter.
Answer:

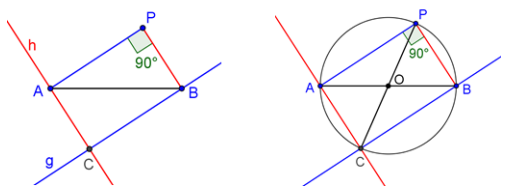
Construct the right triangle, △APB.
Construct the line h that is parallel to \(\overline{P B}\) through point A.
Construct the line g that is parallel to \(\overline{A P}\) through point B.
Let C be the intersection of lines h and g.
The quadrilateral ACBP forms a parallelogram by construction.
By the properties of parallelograms, the adjacent angles are supplementary. Since ∠APB is a right angle, it follows that angles ∠CAP, ∠BCA, and ∠PBC are also right angles. Therefore, the quadrilateral ACBP is a rectangle.

Let O be the intersection of the diagonals \(\overline{A B}\) and \(\overline{C P}\). Then, by the properties of parallelograms, point O is the midpoint of \(\overline{A B}\) and \(\overline{C P}\), so OA = OB = OC = OP. Therefore, O is the center of the circumscribing circle, and the hypotenuse of △APB, \(\overline{A B}\), is a diameter of the circle.

Question 3.
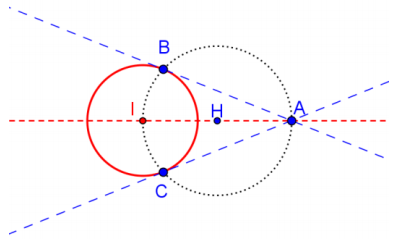
Construct the tangent lines from point P to the circle given below.

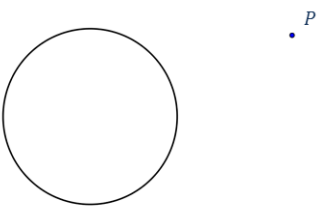
Answer:
Mark any three points A, B, and C on the circle, and construct perpendicular bisectors of \(\overline{A B}\) and \(\overline{B C}\).
Let O be the intersection of the two perpendicular bisectors.

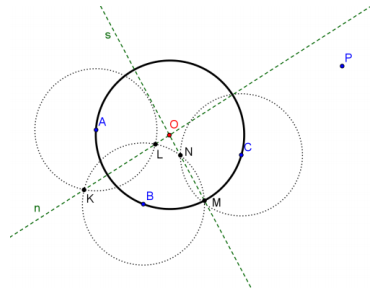
Construct the midpoint H of \(\overline{O P}\).

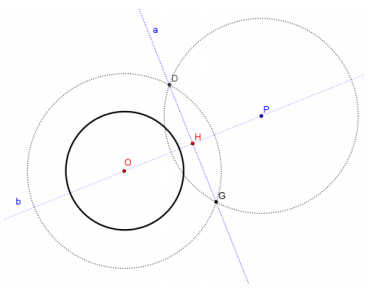
Construct a circle with center H and radius OH.
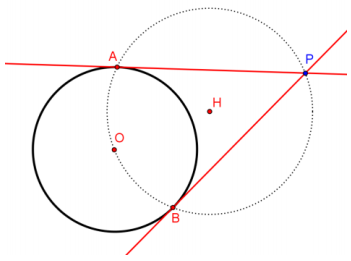
The circle centered at H will intersect the original circle O at points A and B.
Construct two tangent lines \(\overleftrightarrow{P A}\) and \(\overleftrightarrow{P B}\).

Question 4.
Prove that if segments from a point P are tangent to a circle at points A and B, then \(\overline{P A}\) ≅ \(\overline{P B}\).

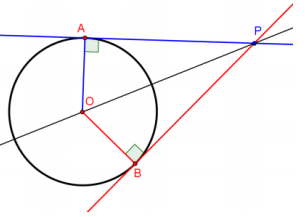
Answer:
Let P be a point outside of a circle with center O, and let A and B be points on the circle so that \(\overline{P A}\) and \(\overline{P B}\) are tangent to the circle. Then, OA = OB, OP = OP, and m∠OAP = m∠OBP = 90°, so △PAO≅ △PBO by the Hypotenuse Leg congruence criterion. Therefore, \(\overline{P A}\) ≅ \(\overline{P B}\) because corresponding parts of congruent triangles are congruent.

Question 5.
Given points A, B, and C so that AB = AC, construct a circle so that \(\overline{A B}\) is tangent to the circle at B and \(\overline{A C}\) is tangent to the circle at C.
Answer:

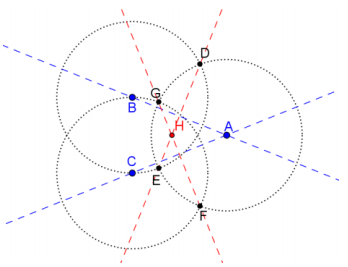
Construct a perpendicular bisector of \(\overline{A B}\).
Construct a perpendicular bisector of \(\overline{A C}\).
The perpendicular bisectors will intersect at point H.
Construct a line through points A and H.
Construct a circle with center H and radius \(\overline{H A}\).
The circle centered at H will intersect \(\overleftrightarrow{H A}\) at I.
Construct a circle centered at I with radius \(\overline{I B}\).

Eureka Math Precalculus Module 4 Lesson 5 Exit Ticket Answer Key

Question 1.
Use a compass and a straightedge to construct the tangent lines to the given circle that pass through the given point.

Answer:

Question 2.
Explain why your construction produces lines that are indeed tangent to the given circle.
Answer:
Since points D and E are on circle C, ∠BDA and ∠BEA are right angles. Thus, \(\overleftrightarrow{A D}\) and \(\overleftrightarrow{A E}\) are tangent to circle B.