Engage NY Eureka Math Precalculus Module 4 Lesson 2 Answer Key
Eureka Math Precalculus Module 4 Lesson 2 Exercise Answer Key
Opening Exercise
The graphs below depict four trigonometric functions. Identify which of the graphs are f(x) = sin(x), g(x) = cos(x), and h(x) = tan(x). Explain how you know.
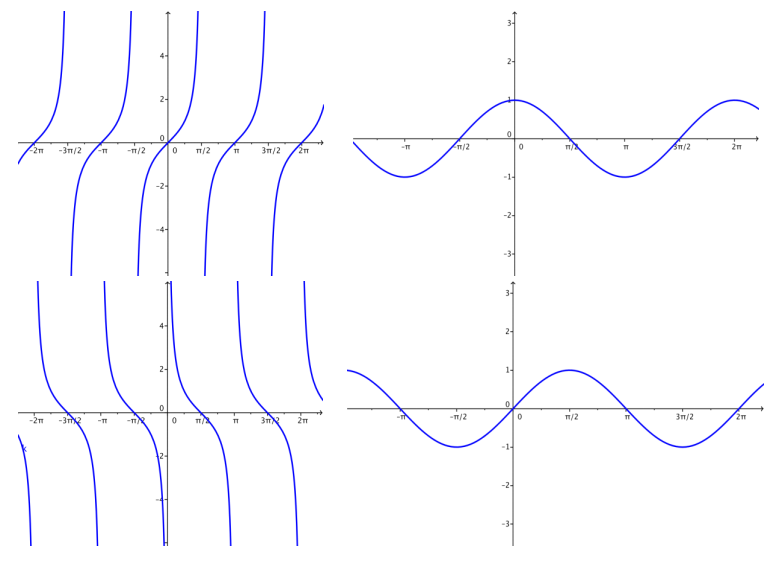
Answer:
The first graph is the graph of the tangent function h(x) = tan(x) because the range of the tangent function is all real numbers, and tan(0) = 0, which rules out the third graph as a possibility.
The second graph (upper right) is the graph of the cosine function g(x) = cos(x) because the range of the cosine function is [ – 1, 1], and cos(0) = 1, ruling out the fourth graph as a possibility.
The fourth graph (bottom right) is the graph of the sine function f(x) = sin(x) because the range of the sine function is [ – 1, 1], and sin(0) = 0.
The third graph (bottom left) is the graph of the cotangent function. (This could be an extension problem for advanced students.)
Exercises 1–4
Exercise 1.
Use the unit circle to evaluate these expressions:
a. sin(\(\frac{17\pi}{4}\))
Answer:
sin(\(\frac{17\pi}{4}\)) = sin(4π + \(\frac{\pi}{4}\)) = sin(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\)
b. cos(\(\frac{19\pi}{6}\))
Answer:
cos(\(\frac{19\pi}{6}\)) = cos(2π + \(\frac{7\pi}{6}\)) = cos(\(\frac{7\pi}{6}\)) = cos(π + \(\frac{\pi}{6}\)) = – cos(\(\frac{\pi}{6}\)) = – \(\frac{\sqrt{3}}{2}\)
c. tan(450π)
Answer:
tan(450π) = tan(450π + 0) = tan(0) = 0
Exercise 2.
Use the identity sin(π + θ) = – sin(θ) for all real – numbered values of θ to verify the identity
Answer:
sin(2π + θ) = sin(θ) for all real – numbered values of θ.
sin(2π + θ) = sin(π + (π + θ)) = – sin(π + θ) = – ( – sin(θ)) = sin(θ)
Exercise 3.
Use your understanding of the symmetry of the sine and cosine functions to evaluate these functions for the given values of θ.
a. sin( – \(\frac{\pi}{2}\))
Answer:
sin( – \(\frac{\pi}{2}\)) = – sin(\(\frac{\pi}{2}\)) = – 1
b. cos( – \(\frac{5\pi}{3}\))
Answer:
cos( – \(\frac{5\pi}{3}\)) = cos(\(\frac{5\pi}{3}\)) = cos(2π – \(\frac{\pi}{3}\)) = cos(\(\frac{\pi}{3}\)) = \(\frac{1}{2}\)
Exercise 4.
Use your understanding of the symmetry of the sine and cosine functions to determine the value of tan( – θ) for all real – numbered values of θ. Determine whether the tangent function is even, odd, or neither.
Answer:
tan(–θ) = \(\frac{\sin ( – \theta)}{\cos ( – \theta)}\) = \(\frac{ – \sin (\theta)}{\cos (\theta)}\) = \(\frac{\sin (\theta)}{\cos (\theta)}\) = – tan(θ)
The tangent function is odd.
Exploratory Challenge/Exercises 5–6
Exercise 5.
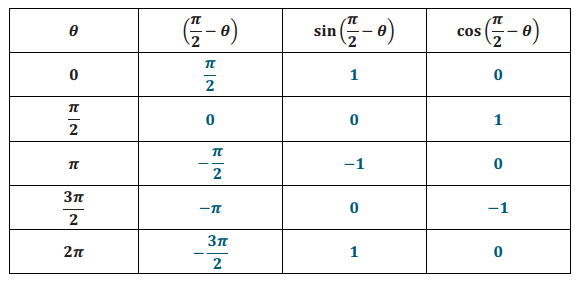
Use your unit circle model to complete the table. Then use the completed table to answer the questions that follow.
Answer:
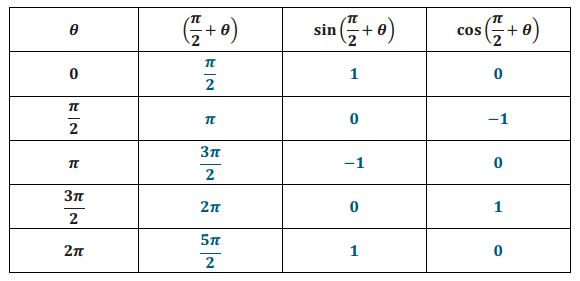
a. What does the value (\(\frac{\pi}{2}\) + θ) represent with respect to the rotation of the carousel?
Answer:
It is a rotation by θ radians counterclockwise from the starting point \(\frac{\pi}{2}\).
b. What pattern do you recognize in the values of sin(\(\frac{\pi}{2}\) + θ) as θ increases from 0 to 2π?
Answer:
Values of sin(\(\frac{\pi}{2}\) + θ) follow the same pattern as values of cos(θ).
c. What pattern do you recognize in the values of cos(\(\frac{\pi}{2}\) + θ) as θ increases from 0 to 2π?
Answer:
Values of cos(\(\frac{\pi}{2}\) + θ) follow the same pattern as values of – sin(θ).
d. Fill in the blanks to formalize these relationships:
sin(\(\frac{\pi}{2}\) + θ) =
cos(\(\frac{\pi}{2}\) + θ) =
Answer:
sin(\(\frac{\pi}{2}\) + θ) = cos(θ)
cos(\(\frac{\pi}{2}\) + θ) = – sin(θ)
Exercise 6.
Use your unit circle model to complete the table. Then use the completed table to answer the questions that follow.
Answer:
a. What does the value (\(\frac{\pi}{2}\) – θ) represent with respect to the rotation of a rider on the carousel?
Answer:
It is a rotation by θ radians clockwise from a point directly in front of the center of the carousel.
b. What pattern do you recognize in the values of sin(\(\frac{\pi}{2}\) – θ) as θ increases from 0 to 2π?
Answer:
Values of sin(\(\frac{\pi}{2}\) – θ) follow the same pattern as values of cos(θ).
c. What pattern do you recognize in the values of cos(\(\frac{\pi}{2}\) – θ) as θ increases from 0 to 2π?
Answer:
Values of cos(\(\frac{\pi}{2}\) – θ) follow the same pattern as values of sin(θ).
d. Fill in the blanks to formalize these relationships:
sin(\(\frac{\pi}{2}\) – θ) =
cos(\(\frac{\pi}{2}\) – θ) =
Answer:
sin(\(\frac{\pi}{2}\) – θ) = cos(θ)
cos(\(\frac{\pi}{2}\) – θ) = sin(θ)
Exercise 7
Use your understanding of the relationship between the sine and cosine functions to verify these statements.
a. cos(\(\frac{4\pi}{3}\)) = sin(\( – \frac{\pi}{6}\))
Answer:
cos(\(\frac{4\pi}{3}\)) = cos(\(\frac{\pi}{2}\) + \(\frac{5\pi}{6}\)) = – sin(\(\frac{5\pi}{6}\)) = – sin(π – \(\frac{5\pi}{6}\)) = – sin(\(\frac{\pi}{6}\)) = sin(\( – \frac{\pi}{6}\))
b. cos(\(\frac{5\pi}{4}\)) = sin(\(\frac{7\pi}{4}\))
Answer:
cos(\(\frac{5\pi}{4}\)) = cos(\(\frac{\pi}{2}\) + \(\frac{3\pi}{4}\)) = – sin(\(\frac{3\pi}{4}\)) = – ( – sin(π + \(\frac{3\pi}{4}\))) = sin(\(\frac{7\pi}{4}\))
Eureka Math Precalculus Module 4 Lesson 2 Problem Set Answer Key
Question 1.
Evaluate the following trigonometric expressions. Show how you used the unit circle to determine the solution.
a. sin(\(\frac{13\pi}{6}\))
Answer:
sin(\(\frac{13\pi}{6}\)) = sin(2π + \(\frac{\pi}{6}\)) = sin(\(\frac{\pi}{6}\)) = \(\frac{1}{2}\)
\(\frac{13\pi}{6}\) is a full rotation more than \(\frac{\pi}{6}\) meaning sin(\(\frac{13\pi}{6}\)) = sin(\(\frac{\pi}{6}\)) = \(\frac{1}{2}\).
b. cos( – \(\frac{5\pi}{3}\))
Answer:
cos( – \(\frac{5\pi}{3}\)) = cos( – (2π – \(\frac{\pi}{3}\))) = cos( – \(\frac{\pi}{3}\)) = cos(\(\frac{\pi}{3}\)) = \(\frac{1}{2}\)
– \(\frac{5\pi}{3}\) is a full rotation less than \(\frac{\pi}{3}\) meaning cos( – \(\frac{5\pi}{3}\)) = cos(\(\frac{\pi}{3}\)) = \(\frac{1}{2}\).
b. tan(\(\frac{25\pi}{4}\))
Answer:
tan(\(\frac{25\pi}{4}\)) = tan(6π + \(\frac{\pi}{4}\)) = tan(\(\frac{\pi}{4}\)) = 1
\(\frac{25\pi}{4}\) is three full rotations more than \(\frac{\pi}{4}\) meaning tan(\(\frac{25\pi}{4}\)) = tan(\(\frac{\pi}{4}\)) = 1.
c. sin( – \(\frac{3\pi}{4}\))
Answer:
sin( – \(\frac{3\pi}{4}\)) = – sin(3\(\frac{\pi}{4}\)) = – sin(π – \(\frac{\pi}{4}\)) = – sin(\(\frac{\pi}{4}\)) = – \(\frac{\sqrt{2}}{2}\)
– \(\frac{3\pi}{4}\) is the same rotation as π + \(\frac{\pi}{4}\) meaning sin( – \(\frac{3\pi}{4}\)) = – sin(\(\frac{\pi}{4}\)) = – \(\frac{\sqrt{2}}{2}\).
d. cos( – \(\frac{5\pi}{6}\))
Answer:
cos( – \(\frac{5\pi}{6}\)) = cos(\(\frac{5\pi}{6}\)) = cos(π – \(\frac{\pi}{6}\)) = – cos(\(\frac{\pi}{6}\)) = – \(\frac{\sqrt{3}}{2}\)
– \(\frac{5\pi}{6}\) is the same rotation as π + \(\frac{\pi}{6}\) meaning cos( – \(\frac{5\pi}{6}\)) = – cos(\(\frac{\pi}{6}\)) = – \(\frac{\sqrt{3}}{2}\).
e. sin(\(\frac{17\pi}{3}\)) sin(\(\frac{17\pi}{3}\)) = sin(4π + \(\frac{5\pi}{3}\)) = sin(\(\frac{5\pi}{3}\)) = sin(2π – \(\frac{\pi}{3}\)) = – sin(\(\frac{\pi}{3}\)) = – \(\frac{\sqrt{3}}{2}\)
\(\frac{17\pi}{3}\) is two full rotations more than \(\frac{5\pi}{3}\) meaning sin(\(\frac{17\pi}{3}\)) = sin(\(\frac{5\pi}{3}\)) = – \(\frac{\sqrt{3}}{2}\).
g. cos(\(\frac{25\pi}{4}\))
Answer:
cos(\(\frac{25\pi}{4}\)) = cos(6π + \(\frac{\pi}{4}\)) = cos(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\)
\(\frac{25\pi}{4}\) is three full rotations more than \(\frac{\pi}{4}\) meaning cos(\(\frac{25\pi}{4}\)) = cos(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\).
h. tan(\(\frac{29\pi}{6}\))
Answer:
tan(\(\frac{29\pi}{6}\)) = tan(4π + \(\frac{5\pi}{6}\)) = tan(\(\frac{5\pi}{6}\)) = tan(π – \(\frac{\pi}{6}\)) = – tan(\(\frac{\pi}{6}\)) = – \(\frac{1}{\sqrt{3}}\)
\(\frac{29\pi}{6}\) is two full rotations more than \(\frac{5\pi}{6}\) meaning tan(\(\frac{29\pi}{6}\)) = – tan(\(\frac{\pi}{6}\)) = – \(\frac{1}{\sqrt{3}}\) = – \(\frac{\sqrt{3}}{3}\).
i. sin( – \(\frac{31\pi}{6}\))
Answer:
sin( – \(\frac{31\pi}{6}\)) = – sin(\(\frac{31\pi}{6}\)) = – sin(4π + \(\frac{7\pi}{6}\)) = – sin(\(\frac{7\pi}{6}\)) = – sin(π + \(\frac{\pi}{6}\)) = – ( – sin(\(\frac{\pi}{6}\))) = \(\frac{1}{2}\)
– \(\frac{31\pi}{6}\) is the same as two full rotations in the clockwise direction plus \(\frac{7\pi}{6}\) more, which is the same rotation as 5\(\frac{\pi}{6}\) meaning sin( – \(\frac{31\pi}{6}\)) = sin(\(\frac{\pi}{6}\)) = \(\frac{1}{2}\).
j. cos( – \(\frac{32\pi}{6}\))
Answer:
cos( – \(\frac{32\pi}{6}\)) = cos(\(\frac{32\pi}{6}\)) = cos(4π + \(\frac{8\pi}{6}\)) = cos(\(\frac{4\pi}{3}\)) = cos(π + \(\frac{\pi}{3}\)) = – cos(\(\frac{\pi}{3}\)) = – \(\frac{1}{2}\)
– \(\frac{32\pi}{6}\) is the same as two full rotations in the clockwise direction plus \(\frac{8\pi}{6}\) or \(\frac{4\pi}{3}\) more, which is the same rotation as π + \(\frac{\pi}{3}\) meaning cos( – \(\frac{32\pi}{6}\)) = – cos(\(\frac{\pi}{3}\)) = – \(\frac{1}{2}\).
k. tan( – \(\frac{18\pi}{3}\))
Answer:
tan( – \(\frac{18\pi}{3}\)) = – tan(\(\frac{18\pi}{3}\)) = tan(6π) = tan(0) = 0
– \(\frac{18\pi}{3}\) is three full rotations in the clockwise direction meaning tan( – \(\frac{18\pi}{3}\)) = tan(0) = 0.
Question 2.
Given each value of β below, find a value of α with 0≤α≤2π so that cos(α) = cos(β) and α≠β.
a. β = \(\frac{3\pi}{4}\)
Answer:
\(\frac{5\pi}{4}\)
b. β = \(\frac{5\pi}{6}\)
Answer:
\(\frac{7\pi}{6}\)
c. β = \(\frac{11\pi}{12}\)
Answer:
\(\frac{13\pi}{12}\)
d. β = 2π
Answer:
0
e. β = \(\frac{7\pi}{5}\)
Answer:
\(\frac{3\pi}{5}\)
f. β = \(\frac{17\pi}{30}\)
Answer:
\(\frac{43\pi}{30}\)
g. β = \(\frac{8\pi}{11}\)
Answer:
\(\frac{14\pi}{11}\)
Question 3.
Given each value of β below, find two values of α with 0≤α≤2π so that cos(α) = sin(β).
a. β = \(\frac{\pi}{3}\)
Answer:
\(\frac{\pi}{6}\), \(\frac{11\pi}{6}\)
b. β = \(\frac{7\pi}{6}\)
Answer:
\(\frac{2\pi}{3}\), \(\frac{4\pi}{3}\)
c. β = \(\frac{3\pi}{4}\)
Answer:
\(\frac{\pi}{4}\), \(\frac{7\pi}{4}\)
d. β = \(\frac{\pi}{8}\)
Answer:
\(\frac{3\pi}{8}\), \(\frac{13\pi}{8}\)
Question 3.
Given each value of β below, find two values of α with 0≤α≤2π so that sin(α) = cos(β).
a. β = \(\frac{\pi}{3}\)
Answer:
\(\frac{\pi}{6}\), \(\frac{5\pi}{6}\)
b. β = \(\frac{5\pi}{6}\)
Answer:
\(\frac{4\pi}{3}\), \(\frac{5\pi}{3}\)
c. β = \(\frac{7\pi}{4}\)
Answer:
\(\frac{\pi}{4}\), \(\frac{3\pi}{4}\)
d. β = \(\frac{\pi}{12}\)
Answer:
\(\frac{5\pi}{12}\), \(\frac{7\pi}{12}\)
Question 5.
Jamal thinks that cos(α – \(\frac{\pi}{4}\)) = sin(α + \(\frac{\pi}{4}\)) for any value of α. Is he correct? Explain how you know.
Answer:
Jamal is correct. Let θ = α + \(\frac{\pi}{4}\). Then θ – \(\frac{\pi}{2}\) = α – \(\frac{\pi}{4}\). We know that cos(\(\frac{\pi}{2}\) – θ) = sin(θ) and that the cosine function is even, so we have cos(θ – \(\frac{\pi}{2}\)) = sin(θ). Then cos(α – \(\frac{\pi}{4}\)) = sin(α + \(\frac{\pi}{4}\)).
Question 6.
Shawna thinks that cos(α – \(\frac{\pi}{3}\)) = sin(α + \(\frac{\pi}{6}\)) for any value of α. Is she correct? Explain how you know.
Answer:
Shawna is correct. Let θ = α + \(\frac{\pi}{6}\). Then θ – \(\frac{\pi}{2}\) = α – \(\frac{\pi}{3}\). We know that cos(\(\frac{\pi}{2}\) – θ) = sin(θ) and that the cosine function is even, so we have cos(θ – \(\frac{\pi}{2}\)) = sin(θ). Then cos(α – \(\frac{\pi}{3}\)) = sin(α + \(\frac{\pi}{6}\)).
Question 7.
Rochelle looked at Jamal and Shawna’s results from Problems 5 and 6 and came up with the conjecture below. Is she correct? Explain how you know. Conjecture: cos(α – β) = sin(α + (\(\frac{\pi}{2}\) – β)).
Answer:
Rochelle is also correct. Because sin(θ + \(\frac{\pi}{2}\)) = cos(θ), we see that
sin(α + (\(\frac{\pi}{2}\) – β)) = sin((α – β) + \(\frac{\pi}{2}\)) = cos(α – β).
Question 8.
A frog is sitting on the edge of a playground carousel with radius 1 meter. The ray through the frog’s position and the center of the carousel makes an angle of measure θ with the horizontal, and his starting coordinates are approximately (0.81, 0.59). Find his new coordinates after the carousel rotates by each of the following amounts.
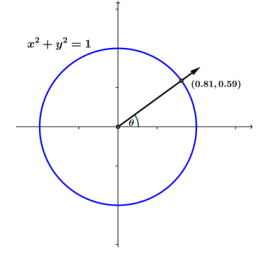
a. \(\frac{\pi}{2}\)
Answer:
cos(θ + \(\frac{\pi}{2}\)) = – sin(θ) = – 0.59
sin(θ + \(\frac{\pi}{2}\)) = cos(θ) = 0.81
New position: ( – 0.59, 0.81)
b. π
Answer:
cos(θ + π) = – cos(θ) = – 0.81
sin(θ + π) = – sin(θ) = – 0.59
New position: ( – 0.81, – 0.59)
c. 2π
Answer:
cos(θ + 2π) = cos(θ) = 0.81
sin(θ + 2π) = sin(θ) = 0.59
New position: (0.81, 0.59)
d. – \(\frac{\pi}{2}\)
Answer:
cos(θ – \(\frac{\pi}{2}\)) = sin(θ) = 0.59
sin(θ – \(\frac{\pi}{2}\)) = – cos(θ) = – 0.81
New position: (0.59, – 0.81)
e. – π
Answer:
cos(θ – π) = – cos(θ) = – 0.81
sin(θ – π) = – sin(θ) = – 0.59
New position: ( – 0.81, – 0.59)
f. \(\frac{\pi}{2}\) – θ
Answer:
cos(θ + (\(\frac{\pi}{2}\) – θ)) = cos(\(\frac{\pi}{2}\)) = 0
sin(θ + (\(\frac{\pi}{2}\) – θ)) = sin(\(\frac{\pi}{2}\)) = 1
New position: (0, 1)
g. π – 2θ
Answer:
cos(θ + (π – 2θ)) = cos(π – θ) = – cos(θ) = – 0.81
sin(θ + (π – 2θ)) = sin(π – θ) = – sin(θ) = 0.59
New position: ( – 0.81, 0.59)
h. – 2θ
Answer:
cos(θ – 2θ) = cos( – θ) = cos(θ) = 0.81
sin(θ – 2θ) = sin( – θ) = – sin(θ) = – 0.59
New position: (0.81, – 0.59)
Eureka Math Precalculus Module 4 Lesson 2 Exit Ticket Answer Key
Question 1.
From the unit circle given, explain why the cosine function is an even function with symmetry about the y – axis, and the sine function is an odd function with symmetry about the origin.
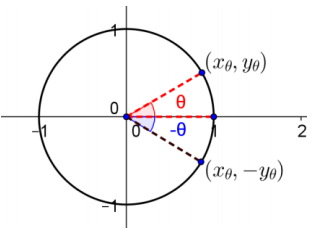
Answer:
Suppose we rotate the point (1, 0) by –θ radians, where θ ≥ 0. This gives the same x – coordinate as rotating by θ radians, so if θ ≥ 0, we have cos( – θ) = cos(θ). Likewise, if θ < 0 and we rotate the point (1, 0) by – θ radians, then the resulting point has the same x – coordinate as rotation of (1, 0) by θ radians. Thus, if θ < 0 then cos( – θ) = cos(θ). Since cos( – θ) = cos(θ) for all real numbers θ, the cosine function is even and is symmetric about the y – axis.
Suppose we rotate the point (1, 0) by –θ radians, where θ ≥ 0. This gives the opposite y – coordinate as rotating by θ radians, so if θ ≥ 0 we have sin( – θ) = – sin(θ). Likewise, if θ < 0 and we rotate the point (1, 0) by – θ radians, then the resulting point has the opposite y – coordinate as rotation of (1, 0) by θ radians. Thus, if θ < 0 then sin( – θ) = – sin(θ). Since sin( – θ) = – sin(θ) for all real numbers θ, the sine function is odd and is symmetric about the origin.
Question 2.
Use the unit circle to explain why cos(\(\frac{\pi}{2}\) – θ) = sin(θ) for θ as shown in the figure to the right.
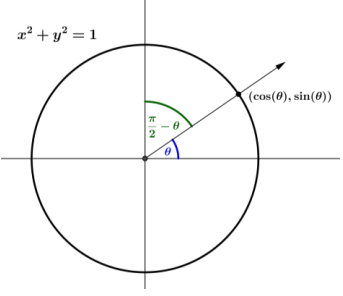
Answer:
The point where the terminal ray intersects the unit circle after rotation by θ has coordinates (cos(θ), sin(θ)). If we draw perpendicular lines from this point to the x – axis and y – axis, we create two triangles. The vertical legs of these triangles both have the same length. The triangle on the left shows that this length is cos(\(\frac{\pi}{2}\) – θ), while the triangle on the right shows that this length is sin(θ). Thus, sin(θ) = cos(\(\frac{\pi}{2}\) – θ)