Eureka Math Precalculus Module 3 Mid Module Assessment Answer Key

Engage NY Eureka Math Precalculus Module 3 Mid Module Assessment Answer Key

Eureka Math Precalculus Module 3 Mid Module Assessment Task Answer Key

Question 1.
a. Write (1 + i)⁷ – (1 – i)⁷ in the form a+bi for some real numbers a and b.
Answer:
The seventh row of Pascal’s triangle is 1 7 21 35 35 21 7 1. Thus:
(1 + i)⁷ = 1 + 7i + 21i² + 35i³ + 35i⁴ + 21i⁵ + 7i⁶ + i⁷
= 1 + 7i – 21 – 35i + 35 + 21i – 7 – i
and
(1 – i)⁷ = 1 – 7i + 21i² – 35i³ + 35i⁴ – 21i⁵ + 7i⁶ –i⁷
= 1 – 7i – 21 + 35i + 35 – 21i – 7 + i.
Their difference is
(1 + i)⁷ – (1 – i)⁷ = 14i – 70i + 42i – 2i = –16i.
This answer is in the form a + bi with a = 0 and b = –16.

b. Explain how Pascal’s triangle allows you to compute the coefficient of x² y² when (x – y)⁵ is expanded.
Answer:
The fifth row of Pascal’s triangle is 1 5 10 10 5 1 . Thus:
(x – y)⁵ = (x + (–y ))⁵
= x⁵ + 5 x⁴ (–y ) + 10 x³ (–y )² + 10 x² (–y )³ + 5x (–y )⁴ + (–y )⁵
= x⁵ – 5 x⁴ y + 10 x³ y² – 10 x² y³ + 5x y⁴ – y⁵
The coefficient of x² y³ is –10 .

Question 2.
Verify that the fundamental theorem of algebra holds for the fourth-degree polynomial p given by p(z) = z⁴ + 1 by finding four zeros of the polynomial and writing the polynomial as a product of four linear terms. Be sure to make use of the polynomial identity given below.
x⁴ – a⁴ = (x – a)(x + a)(x – ai)(x + ai)
Answer:
We have p (z ) = z⁴ – (–1) suggesting we need to find a number a so that a⁴ = –1 . This means a² = i or a² = –i . Since we need to find only one value for a that works, let’s select a² = i .
Now i has modulus 1 and argument \(\frac{\pi}{2}\) , so a complex number a with modulus 1 and argument \(\frac{\pi}{4}\) satisfies a² = i . So, a = cos ⁡(\(\frac{\pi}{4}\)) + i sin ⁡(\(\frac{\pi}{4}\)) = \(\frac{1+i}{\sqrt{2}}\).
(And we check: (\(\frac{1+i}{\sqrt{2}}\))² = \(\frac{1+2 i-1}{2}\) = i .)
So, p (z ) = z⁴ – (\(\frac{1+i}{\sqrt{2}}\))⁴ = (z – \(\frac{1+i}{\sqrt{2}}\))(z + \(\frac{1+i}{\sqrt{2}}\))(z – \(\frac{1-i}{\sqrt{2}}\))(z + \(\frac{1-i}{\sqrt{2}}\)) following the polynomial identity given. Thus, we see that p does indeed factor into four linear terms and has four roots: \(\frac{1+i}{\sqrt{2}}\), – \(\frac{1+i}{\sqrt{2}}\), \(\frac{1-i}{\sqrt{2}}\), and –\(\frac{1-i}{\sqrt{2}}\).

Question 3.
Consider the cubic polynomial p given p(z)= z³-8.
a. Find a real number root to the polynomial.
Answer:
z = 2 is a root.

b. Write p(z) as a product of three linear terms.
Answer:
We have z³ – 8 = (z – 2)( z² + 2z + 4) .
Now z² + 2z + 4 = 0 when z = \(\frac{-2 \pm \sqrt{4-1.6}}{2}\) = –1 ± \(\sqrt{3}\)i showing that z² + 2z + 4 factors as (z + 1 + \(\sqrt{3}\)i)(z + 1 – \(\sqrt{3}\)i) .
Thus:
p (z ) = (z – 2)(z + 1 + \(\sqrt{3}\)i)(z + 1 – \(\sqrt{3}\)i) .

Consider the degree-eight polynomial q given by q(z)=z⁸-2⁸.
c. What is the largest possible number of distinct roots the polynomial q could possess? Briefly explain your answer.
Answer:
By the fundamental theorem of algebra, a degree-eight polynomial has at most 8 distinct roots.

d. Find all the solutions to q(z)=0.
Answer:
We have
q (z )=z⁸ – 2⁸
=( z⁴ – 2⁴)( z⁴ + 2⁴)
=(z² – 2²)(z² + 2² )(z⁴ + 2⁴)
=(z – 2)(z + 2)(z – 2i )(z + 2i )(z² – 4i )(z² + 4i ).
We see the zeros:
z = 2,z = –2,z = 2i, and z = –2i .
Going further, we need to also solve z² – 4i = 0 and z² + 4i = 0 .

Now if (a + bi) = 4i , we have a² – b² = 0 (giving a = ±b ) and 2ab = 4 (i.e., ab = 2 ). If a = b , we get a² = 2 ; so, a = b = \(\sqrt{2}\)or a = b = – \(\sqrt{2}\). If a = –b we get a² = –2 , which has no solution. So we see
If z² – 4i = 0 , then z = \(\sqrt{2}\) + \(\sqrt{2}\)i or z = – \(\sqrt{2}\) – \(\sqrt{2}\)i .

The same work shows the following:
If z² + 4i = 0 , then z = \(\sqrt{2}\) – \(\sqrt{2}\)i or z = – \(\sqrt{2}\) + \(\sqrt{2}\)i .

We have thus identified the eight zeros of q .

Question 4.
a. A right circular cylinder of radius 5 cm and height 5 cm contains half a sphere of radius 5 cm as shown.

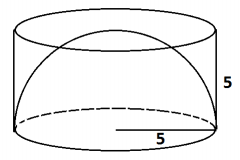
Use Cavalieri’s principle to explain why the volume inside this cylinder but outside the hemisphere is equivalent to the volume of a circular cone with base of radius 5 cm and height 5 cm.
Answer:
Look at a horizontal cross-section of the region inside the cylinder but outside the hemisphere. It is ring-shaped—the region between two circular discs.

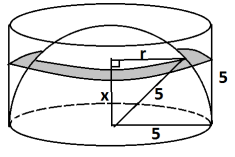
If the height of the cross-section in centimeters is x as shown (0 ≤ x ≤ 5), and the length r in centimeters is the distance from the vertical line of symmetry of the figure to the surface of the hemisphere as shown, then the area of the horizontal cross-section in square centimeters is π 5² – π r² , or π(25 – r²). By the Pythagorean theorem, (look at another radius of the sphere) this equals π x² , which is the area of a circle of radius x .
If we draw the solid figure whose horizontal cross-section at height x in centimeters for 0 ≤ x ≤ 5 is a circle of radius x , we get a circular cone of height 5 cm and base radius of 5 cm.

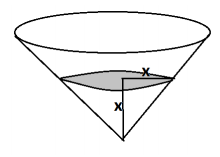
By Cavalieri’s principle, the volume of the region inside the cylinder but outside the hemisphere is equivalent to the volume of this circular cone.

b. Three congruent solid balls are packaged in a cardboard cylindrical tube. The cylindrical space inside the tube has dimensions such that the three balls fit snugly inside that tube as shown.

Each ball is composed of material with density 15 grams per cubic centimeter. The space around the balls inside the cylinder is filled with aerated foam with a density of 0.1 grams per cubic centimeter.

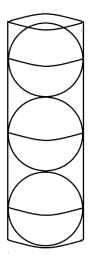
i. Ignoring the cardboard of the tube, what is the average density of the contents inside of the tube?
ii. If the contents inside the tube, the three balls and the foam, weigh 150 grams to one decimal place, what is the weight of one ball in grams?
Answer:
From part (a), since the volume of a cone is one-third the volume of a cylinder with the same base and same height, the space inside the cylinder and outside the hemisphere in that question is one-third the volume of the cylinder. This means that the volume of the hemisphere is double the volume of this space.

For three balls packed in a cylinder, we have six copies of the situation analyzed in part (a). Thus, the volume of foam inside the package and outside of the balls is one-half the total volume of the balls.

Let V_f denote the total volume of the foam and V_b the total volume of the balls. Then we have V_f = \(\frac{1}{2}\) V_b, or V_b = 2 V_f.

Let M_f be the total mass of the foam and M_b be the total mass of the balls. Density is mass per volume, so the densities in grams per cubic centimeter are as follows:
density of the foam: \(\frac{M_{f}}{V_{f}}\) = 0.1
density of the balls: \(\frac{M_{b}}{V_{b}}\) = 15 .

i) Density_average = \(\frac{M_{f}+M_{b}}{V_{f}+V_{b}}\)
= \(\frac{M_{f}+M_{b}}{3 V_{f}}\)
= \(\frac{1}{3}\) ∙ \(\frac{M_{f}}{V_{f}}\) + \(\frac{M_{b}}{3 V_{f}}\)
= \(\frac{1}{3}\) (0.1 ) + \(\frac{2}{3}\) ∙ \(\frac{M_{b}}{V_{b}}\)
= \(\frac{1}{3}\) (0.1 ) + \(\frac{2}{3}\) (15 )
= \(\frac{1}{30}\) + 10
≈ 10.033
The average density of the contents is approximately 10.033 grams/cubic centimeter.

ii) As the weight of the foam is negligible, we expect each ball to weigh approximately 50 grams. To get the exact weight, use
Total mass = total volume × average density.
(10 + \(\frac{1}{30}\)) × (V_f + V_b) = 150
(10 + \(\frac{1}{30}\)) × \(\frac{3}{2}\) V_b = 150
V_b = \(\) = \(\frac{3000}{301}\)
Since we have 3 balls, we must divide by 3: \(\frac{1}{3}\) × \(\frac{3000}{301}\) = \(\frac{1000}{301}\). The volume of one ball is \(\frac{1000}{301}\) cubic centimeters.
As the density of each ball is 15 grams per cubic centimeter: 15 × \(\frac{1000}{301}\) ≈ 49.8 .
The weight of one ball is approximately 49.8 grams.

Question 5.
a. Consider the two points F(-9,0) and G(9,0) in the coordinate plane. What is the equation of the ellipse given as the set of all points P in the coordinate plane satisfying FP+PG=30? Write the equation in the form \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\)=1 with a and b real numbers, and explain how you obtain your answer.
Answer:
Suppose the ellipse described crosses the positive x-axis at x = a and the positive y-axis at b . Let k be the distance between G and the positive x-intercept as shown.

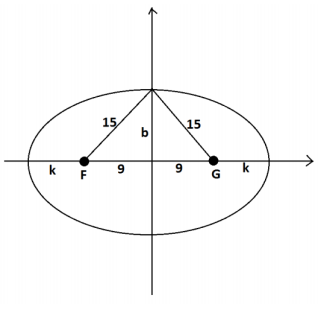
For the point P(0,b) on the ellipse, we have FP + PG = 30 . By symmetry, this means PG = 15 , and by the Pythagorean theorem, b = \(\sqrt{15^{2}-9^{2}}\) = 12 .

For the point Q(a,0) on the ellipse, we have GP + PF = 18 + 2k = 30 , giving
k = 6 and a = 9 + k = 15 . Thus, the equation of the ellipse is \(\frac{x^{2}}{15^{2}}+\frac{y^{2}}{1.2^{2}}\) = 1 .
OR
For any point P(x,y) on the ellipse:
FP = \(\sqrt{(x+9)^{2}+y^{2}}\)
PG = \(\sqrt{(x-9)^{2}+y^{2}}\)
and FP + PG = 30 reads
\(\sqrt{(x+9)^{2}+y^{2}}\) + \(\sqrt{(x-9)^{2}+y^{2}}\) = 30.
This can be rewritten as follows:
\(\sqrt{(x-9)^{2}+y^{2}}\) = 30 – \(\sqrt{(x+9)^{2}+y^{2}}\).

Squaring gives the following:
(x – 9 )² + y ² =900 + (x + 9 )² + y ² – \(60 \sqrt{(x+9)^{2}+y^{2}}\)
–18x=900 + 18x – \(60 \sqrt{(x+9)^{2}+y^{2}}\)
\(60 \sqrt{(x+9)^{2}+y^{2}}\) = 900 + 36x
\(10 \sqrt{(x+9)^{2}+y^{2}}\) = 150 + 6x.

Squaring one more time produces the following:
100 ((x + 9 )² + y ² )=22500 + 36 x ² + 1800x
100 x ² + 1800x + 8100 + 100 y ² =22500 + 36 x ² + 1800x
64 x ² + 100 y ² = 14400
\(\frac{x^{2}}{225}+\frac{y^{2}}{1.44}\) =1.

Thus, any point P(x,y) on the ellipse must be a solution to the equation
\(\frac{x^{2}}{15^{2}}+\frac{y^{2}}{12^{2}}\) = 1.

b. Consider again the two points F(-9,0) and G(9,0) in the coordinate plane. The equation of the hyperbola defined by |FP-PG|=k for some constant k is given by \(\frac{x^{2}}{25}-\frac{y^{2}}{56}\) = 1. What is the value of k?
Answer:
Consider the equation
\(\frac{x^{2}}{25}-\frac{y^{2}}{56}\) = 1.
Setting y = 0 shows that P(5,0) is a point on the hyperbola. Then FP = 4 and PG = 14 , so k = |FP – PG | = 10 .