Eureka Math Precalculus Module 3 Lesson 8 Answer Key

Engage NY Eureka Math Precalculus Module 3 Lesson 8 Answer Key

Eureka Math Precalculus Module 3 Lesson 8 Exercise Answer Key

Exercises
Exercise 1.
Let F(0, 5) and G(0, – 5) be the foci of a hyperbola. Let the points P(x,y) on the hyperbola satisfy either PF – PG = 6 or PG – PF = 6. Use the distance formula to derive an equation for this hyperbola, writing your answer in the form \(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1.
Answer:
PG – PF = 6
\(\sqrt{x^{2} + (y + 5)^{2}}\) – \(\sqrt{x^{2} + (y – 5)^{2}}\) = 6
\(\sqrt{x^{2} + (y + 5)^{2}}\) = 6 + \(\sqrt{x^{2} + (y – 5)^{2}}\)
x² + (y² + 10y + 25) = 36 + 12\(\sqrt{x^{2} + (y – 5)^{2}}\) + (x² + y² – 10y + 25)
20y – 36 = 12\(\sqrt{x^{2} + (y – 5)^{2}}\)
5y – 9 = 3\(\sqrt{x^{2} + (y – 5)^{2}}\)
25y² – 90y + 81 = 9(x² + y² – 10y + 25)
25y² – 90y + 81 = 9x² + 9y² – 90y + 225
16y² – 9x² = 144
\(\frac{y^{2}}{9}\) – \(\frac{x^{2}}{16}\) = 1

Exercise 2.
Where does the hyperbola described above intersect the y – axis?
Answer:
The curve intersects the y – axis at (0,3) and (0, – 3).

Exercise 3.
Find an equation for the line that acts as a boundary for the portion of the curve that lies in the first quadrant.
Answer:
For large values of x, \(\frac{y}{3}\)≈\(\frac{x}{4}\), so the line y = \(\frac{3}{4}\) x is the boundary for the curve in the first quadrant.

Exercise 4.
Sketch the graph of the hyperbola described above.
Answer:

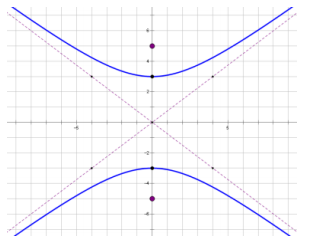
Eureka Math Precalculus Module 3 Lesson 8 Problem Set Answer Key

Question 1.
For each hyperbola described below: (1) Derive an equation of the form \(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1 or \(\frac{y^{2}}{b^{2}}\) – \(\frac{x^{2}}{a^{2}}\) = 1. (2) State any x – or y – intercepts. (3) Find the equations for the asymptotes of the hyperbola.
a. Let the foci be A( – 2,0) and B(2,0), and let P be a point for which either PA – PB = 2 or PB – PA = 2.
Answer:
i. x² – \(\frac{y^{2}}{3}\) = 1
ii. ( – 1,0), (1,0); no y – intercepts
iii. y≈\(\sqrt{3}\) x, so y = ±\(\sqrt{3}\) x

b. Let the foci be A( – 5,0) and B(5,0), and let P be a point for which either PA – PB = 5 or PB – PA = 5.
Answer:
i. \(\frac{x^{2}}{\frac{25}{4}}\) – \(\frac{y^{2}}{\frac{75}{4}}\) = 1
ii. ( – 2.5,0), (2.5,0); no y – intercepts
iii. y≈\(\frac{\sqrt{75}}{2}\)⋅\(\frac{2}{5}\) x = \(\sqrt{3}\) x, so y = ±\(\sqrt{3}\) x

c. Consider A(0, – 3) and B(0,3), and let P be a point for which either PA – PB = 2.5 or PB – PA = 2.5.
Answer:
i. \(\frac{y^{2}}{\frac{9}{4}}\) – \(\frac{x^{2}}{\frac{27}{4}}\) = 1
ii. (0,1.5), (0, – 1.5); no x – intercepts
iii. y≈\(\frac{3}{2}\)⋅\(\frac{2}{\sqrt{27}}\) x = \(\frac{1}{\sqrt{3}}\)x, so y = ±\(\frac{\sqrt{3}}{3}\)x

d. Consider A(0, – \(\sqrt{2}\)) and B(0,\(\sqrt{2}\)), and let P be a point for which either PA – PB = 2 or PB – PA = 2.
Answer:
i. y² – x² = 1
ii. (0,1), (0, – 1); no x – intercepts.
iii. y = ±x

Question 2.
Graph the hyperbolas in parts (a)–(d) in Problem 1.
Answer:
a.

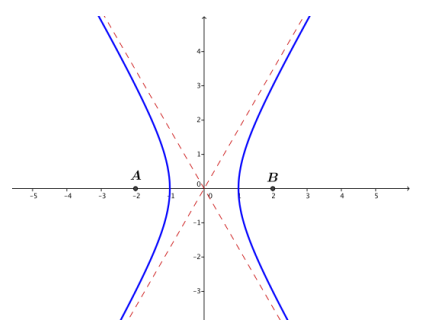
b.

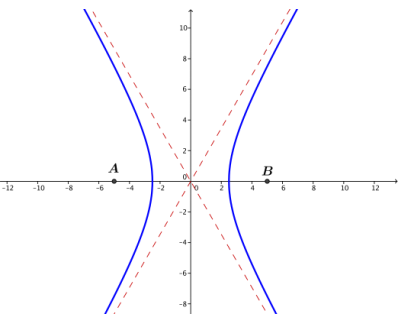
c.

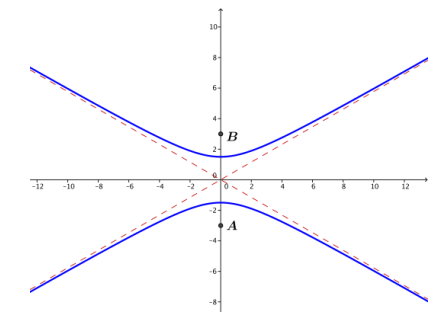
d.

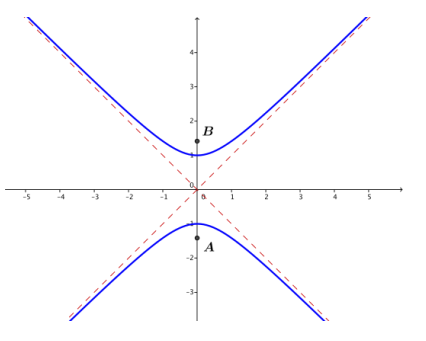
Question 3.
For each value of k specified in parts (a)–(e), plot the set of points in the plane that satisfy the equation
x² – y² = k.
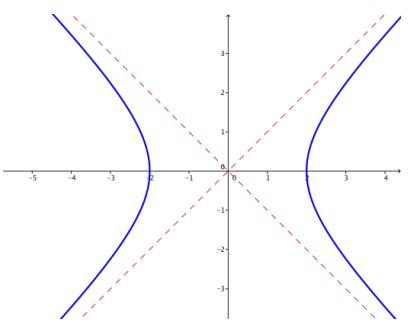
a. k = 4
Answer:

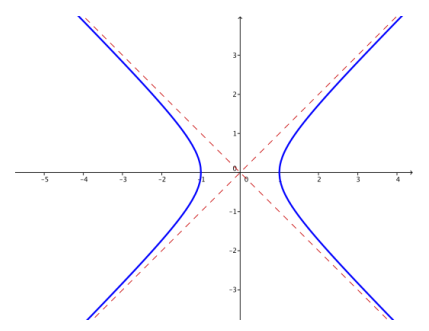
b. k = 1
Answer:

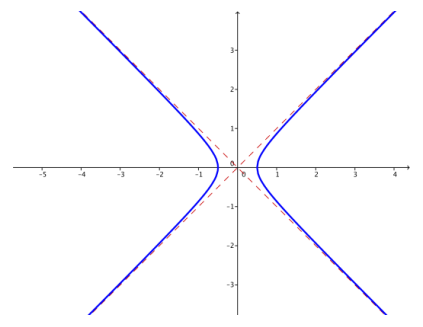
c. k = \(\frac{1}{4}\)
Answer:

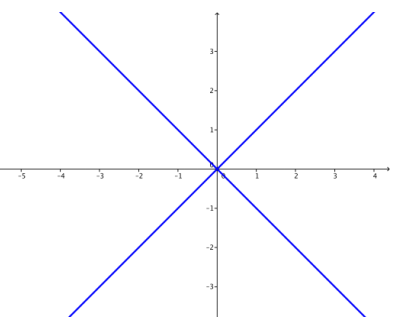
d. k = 0
Answer:

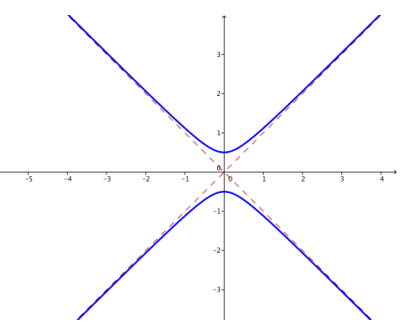
e. k = – \(\frac{1}{4}\)
Answer:

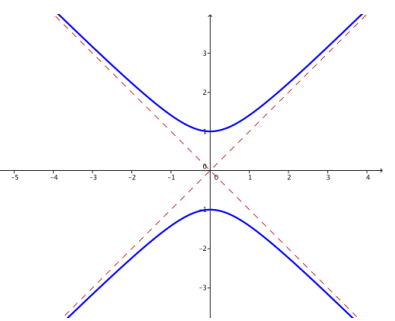
f. k = – 1
Answer:

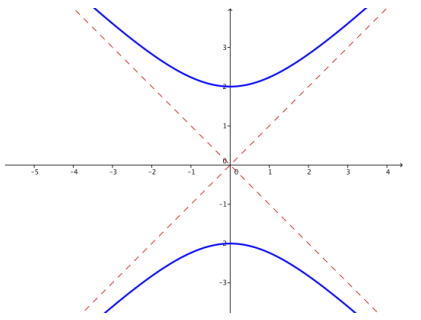
g. k = – 4
Answer:

h. Describe the hyperbolas x² – y² = k for different values of k. Consider both positive and negative values of k, and consider values of k close to zero and far from zero.
Answer:
If k is close to zero, then the hyperbola is very close to the asymptotes y = x and y = – x, appearing almost to have corners as the graph crosses the x – axis. If k is far from zero, the hyperbola gets farther from the asymptotes near the center. If k > 0, then the hyperbola crosses the x – axis, opening to the right and left, and if k<0, then the hyperbola crosses the y – axis, opening up and down.

i. Are there any values of k so that the equation x² – y² = k has no solution?
Answer:
No. The equation x² – y² = k always has solutions. The solution points lie on either two intersecting lines or on a hyperbola.

Question 4.
For each value of k specified in parts (a)–(e), plot the set of points in the plane that satisfy the equation
\(\frac{x^{2}}{k}\) – y² = 1.
a. k = – 1
Answer:
There is no solution to the equation \(\frac{x^{2}}{ – 1}\) – y² = 1, because there are no real numbers x and y so that x² + y² = – 1.

b. k = 1
Answer:

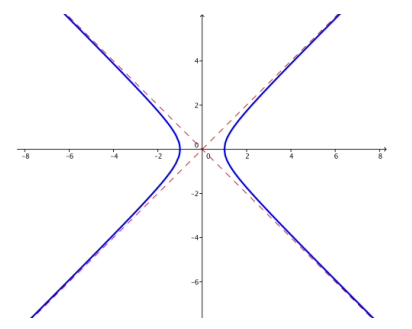
c. k = 2
Answer:

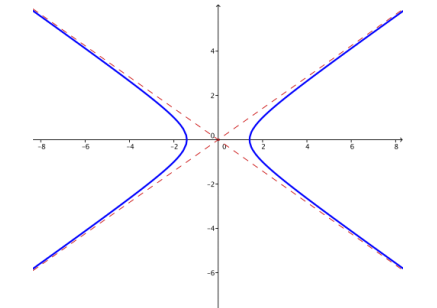
d. k = 4
Answer:

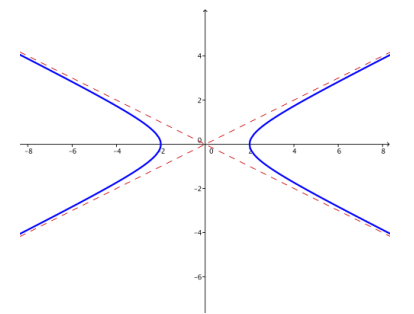
e. k = 10
Answer:

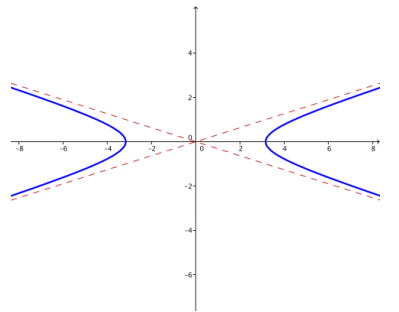
f. k = 25
Answer:

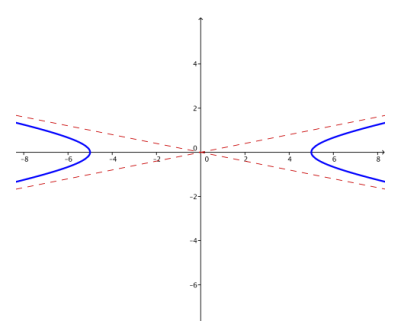
g. Describe what happens to the graph of \(\frac{x^{2}}{k}\) – y² = 1 as k → ∞.
Answer:
As k → ∞, it appears that the hyperbolas with equation \(\frac{x^{2}}{k}\) – y² = 1 get flatter; the x – intercepts get farther from the center at the origin, and the asymptotes get less steep.

Question 5.
For each value of k specified in parts (a)–(e), plot the set of points in the plane that satisfy the equation
x² – \(\frac{y^{2}}{k}\) = 1.
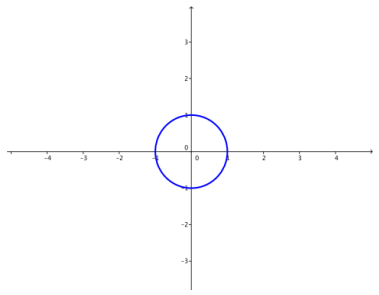
a. k = – 1
Answer:

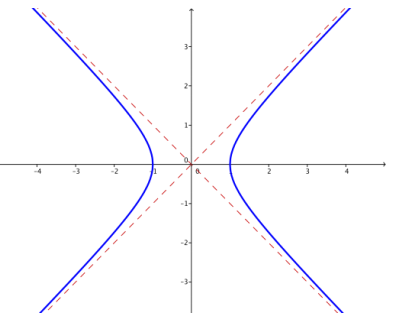
b. k = 1
Answer:

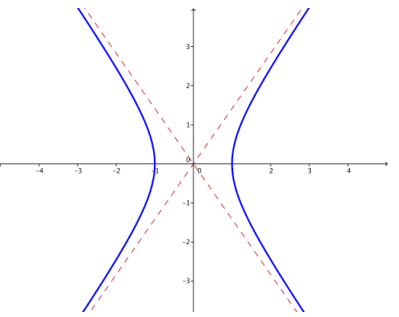
c. k = 2
Answer:

d. k = 4
Answer:

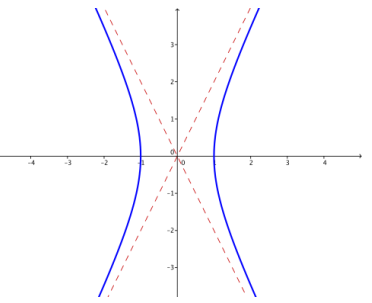
e. k = 10
Answer:

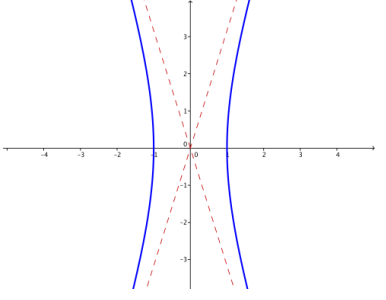
f. Describe what happens to the graph x² – \(\frac{y^{2}}{k}\) = 1 as k → ∞.
Answer:
As k → ∞, the hyperbola with equation x² – \(\frac{y^{2}}{k}\) = 1 is increasingly stretched vertically. The center and intercepts do not change, but the steepness of the asymptotes increases.

Question 6.
An equation of the form ax² + bx + cy² + dy + e = 0 where a and c have opposite signs might represent a hyperbola.
a. Apply the process of completing the square in both x and y to convert the equation
Answer:
9x² – 36x – 4y² – 8y – 4 = 0 to one of the standard forms for a hyperbola: \(\frac{(x – h)^{2}}{a^{2}}\) – \(\frac{(y – k)^{2}}{b^{2}}\) = 1 or \(\frac{(y – k)^{2}}{b^{2}}\) – \(\frac{(x – h)^{2}}{a^{2}}\) = 1.
9x² – 36x – 4y² – 8y = 4
9(x² – 4x) – 4(y² + 2y) = 4
9(x² – 4x + 4) – 4(y² + 2y + 1) = 4 + 36 – 4
9(x – 2)² – 4(y + 1)² = 36
\(\frac{(x – 2)^{2}}{4}\) – \(\frac{(y + 1)^{2}}{9}\) = 1

b. Find the center of this hyperbola.
Answer:
The center is (2, – 1).

c. Find the asymptotes of this hyperbola.
Answer:
\(\frac{x – 2}{2}\) = ±\(\frac{y + 1}{3}\)
y = \(\frac{3}{2}\) x – 4 or y = – \(\frac{3}{2}\) x + 2

d. Graph the hyperbola.
Answer:

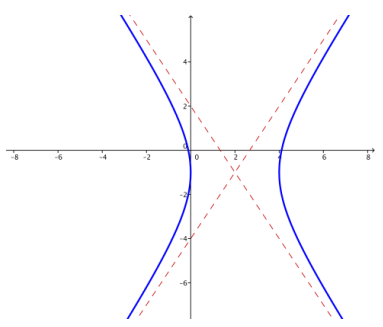
Question 7.
For each equation below, identify the graph as either an ellipse, a hyperbola, two lines, or a single point. If possible, write the equation in the standard form for either an ellipse or a hyperbola.
a. 4x² – 8x + 25y² – 100y + 4 = 0
Answer:
In standard form, this is the equation of an ellipse: \(\frac{(x – 1)^{2}}{25}\) + \(\frac{(y – 2)^{2}}{4}\) = 1.

b. 4x² – 16x – 9y² – 54y – 65 = 0
Answer:
When we try to put this equation in standard form, we find \(\frac{(x – 2)^{2}}{9}\) – \(\frac{(y + 3)^{2}}{4}\) = 0, which gives
(\(\frac{x – 2}{3}\) = ±\(\frac{y + 3}{2}\). These are the lines with equation y = \(\frac{1}{3}\) (2x – 13) and y = \(\frac{1}{3}\) ( – 2x – 5).

c. 4x² + 8x + y² + 2y + 5 = 0
Answer:
When we try to put this equation in standard form, we find (x + 1)² + \(\frac{(y + 1)^{2}}{4}\) = 0. The graph of this equation is the single point ( – 1, – 1).

d. – 49x² + 98x + 4y² – 245 = 0
Answer:
In standard form, this is the equation of a hyperbola: \(\frac{y^{2}}{49}\) – \(\frac{(x – 1)^{2}}{4}\) = 1.

e. What can you tell about a graph of an equation of the form ax² + bx + cy² + dy + e = 0 by looking at the coefficients?
Answer:
There are two categories; if the coefficients a and c have the same sign, then the graph is either an ellipse, a point, or an empty set. If the coefficients a and c have opposite signs, then the graph is a hyperbola or two intersecting lines. We cannot tell just by looking at the coefficients which of these sub – cases hold.

Eureka Math Precalculus Module 3 Lesson 8 Exit Ticket Answer Key

Question 1.
Let F( – 4,0) and B(4,0) be the foci of a hyperbola. Let the points P(x,y) on the hyperbola satisfy either PF – PG = 4 or PG – PF = 4. Derive an equation for this hyperbola, writing your answer in the form \(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1.
Answer:
PF = \(\sqrt{(x + 4)^{2} + y^{2}}\)
PB = \(\sqrt{(x – 4)^{2} + y^{2}}\)
\(\sqrt{(x + 4)^{2} + y^{2}}\) = 4 + \(\sqrt{(x – 4)^{2} + y^{2}}\)
(x + 4)² + y² = 16 + 8\(\sqrt{(x – 4)^{2} + y^{2}}\) + (x – 4)² + y²
x² + 8x + 16 + y² = 16 + 8\(\sqrt{(x – 4)^{2} + y^{2}}\) + x² – 8x + 16 + y²
16x – 16 = 8\(\sqrt{(x – 4)^{2} + y^{2}}\)
2x – 2 = \(\sqrt{(x – 4)^{2} + y^{2}}\)
4x² – 8x + 4 = (x – 4)² + y²
4x² – 8x + 4 = x² – 8x + 16 + y²
3x² – y² = 12
\(\frac{x^{2}}{4}\) – \(\frac{y^{2}}{12}\) = 1