Eureka Math Precalculus Module 3 Lesson 3 Answer Key

Engage NY Eureka Math Precalculus Module 3 Lesson 3 Answer Key

Eureka Math Precalculus Module 3 Lesson 3 Exploratory Challenge Answer Key

Exploratory Challenge
Consider the equation x³ = 1.
a. Use the graph of f(x) = x³ – 1 to explain why 1 is the only real number solution to the equation x³ = 1.

Answer:
From the graph, you can see that the point (1,0) is the x – intercept of the function. That means that 1 is a zero of the polynomial function and thus is a solution to the equation x³ – 1 = 0.

b. Find all of the complex solutions to the equation x³ = 1. Come up with as many methods as you can for finding the solutions to this equation.
Answer:
Method 1: Factoring Using a Polynomial Identity and Using the Quadratic Formula
Rewrite the equation in the form x³ – 1 = 0, and use the identity a³ – b³ = (a – b)(a² + ab + b²) to factor x³ – 1.
x³ – 1 = 0
(x – 1)(x² + x + 1) = 0
Then
x – 1 = 0 or x² + x + 1 = 0.
The solution to the equation x – 1 = 0 is 1. The quadratic formula gives the other solutions.
x = \(\frac{ – 1 \pm \sqrt{ – 3}}{2}\) = \(\frac{ – 1 \pm i \sqrt{3}}{2}\)
So, the solution set is
{1, – \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i, – \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i}.

Method 2: Using the Polar Form of a Complex Number
The solutions to the equation x³ = 1 are the cube roots of 1.
The number 1 has modulus 1 and argument 0 (or any rotation that terminates along the positive real axis such as 2π or 4π, etc.).
The modulus of the cube roots of 1 is \(\sqrt[3]{1}\) = 1. The arguments are solutions to
3θ = 0
3θ = 2π
3θ = 4π
3θ = 6π.
The solutions to these equations are 0, \(\frac{2\pi}{3}\), \(4\frac{\pi}{3}\), 2π, …. Since the rotations cycle back to the same locations in the complex plane after the first three, we only need to consider 0, \(\frac{2\pi}{3}\), and \(\frac{4\pi}{3}\).
The solutions to the equation x³ = 1 are
1(cos⁡(0) + i sin⁡(0) ) = 1
1(cos⁡(\(\frac{2\pi}{3}\)) + i sin⁡(\(\frac{2\pi}{3}\))) = – \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i
1(cos⁡(\(\frac{4\pi}{3}\)) + i sin⁡(\(\frac{4\pi}{3}\))) = – \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i.

Method 3: Using the Techniques of Lessons 1 and 2 from This Module
Let x = a + bi; then (a + bi)³ = 1 + 0i.
Expand (a + bi)³, and equate the real and imaginary parts with 1 and 0.
(a + bi)³ = (a + bi)(a² + 2abi – b²) = a³ + 3a² bi – 3ab² – b³ i
The real part of (a + bi)³ is a³ – 3ab², and the imaginary part is 3a³ b – b³. Thus, we need to solve the system
a³ – 3ab² = 1
3a² b – b³ = 0.
Rewriting the second equation gives us
b(3a² – b²) = 0.
If b = 0, then a³ = 1 and a = 1. So, a solution to the equation x³ = 1 is 1 + 0i = 1.
If 3a² – b² = 0, then b² = 3a², and by substitution,
a³ – 3a(3a² ) = 1
– 8a³ = 1
a³ = – \(\frac{1}{8}\) .
This equation has one real solution: – \(\frac{1}{2}\). If = – \(\frac{1}{2}\), then b² = 3 ( – \(\frac{1}{2}\))² = \(\frac{3}{4}\), so b = \(\frac{\sqrt{3}}{2}\) or = – \(\frac{\sqrt{3}}{2}\). The other two solutions to the equation x³ = 1 are – \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i and – \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i.

Eureka Math Precalculus Module 3 Lesson 3 Exercise Answer Key

Opening Exercise
Consider the equation xⁿ = 1 for positive integers n.
a. Must an equation of this form have a real solution? Explain your reasoning.
Answer:
The number 1 will always be a solution to xⁿ = 1 because 1ⁿ = 1 for any positive integer n.

b. Could an equation of this form have two real solutions? Explain your reasoning.
Answer:
When n is an even number, both 1 and – 1 are solutions. The number 1 is a solution because 1ⁿ = 1 for any positive integer. The number – 1 is a solution because ( – 1)ⁿ = ( – 1)^2k where k is a positive integer if n is even and
( – 1)^2k = (( – 1)²)^k = 1^k = 1.

c. How many complex solutions are there for an equation of this form? Explain how you know.
Answer:
We can rewrite the equation in the form xⁿ – 1 = 0. The solutions to this polynomial equation are the roots of the polynomial p(x) = xⁿ – 1. The fundamental theorem of algebra says that the polynomial
p(x) = xⁿ – 1 factors over the complex numbers into the product of n linear terms. Each term identifies a complex root of the polynomial. Thus, a polynomial equation of degree n has at most n solutions.

Exercises
Solutions to the equation xⁿ = 1 for positive integers n are called the nth roots of unity.
Exercise 1.
What are the square roots of unity in rectangular and polar form?
Answer:
The square roots of unity in rectangular form are the real numbers 1 and – 1.
In polar form, 1(cos⁡(0) + i sin⁡(0) ) and 1(cos⁡(π) + i sin⁡(π) ).

Exercise 2.
What are the fourth roots of unity in rectangular and polar form? Solve this problem by creating and solving a polynomial equation. Show work to support your answer.
Answer:
The fourth roots of unity in rectangular form are 1, – 1, i, – i.
x⁴ = 1
x⁴ – 1 = 0
(x² – 1)(x² + 1) = 0
The solutions to x² – 1 = 0 are 1 and – 1. The solutions to x² + 1 = 0 are i and – i.
In polar form, 1(cos⁡(0) + i sin⁡(0) ), 1(cos⁡(\(\frac{\pi}{2}\)) + i sin⁡(\(\frac{\pi}{2}\)) ), 1(cos⁡(π) + i sin⁡(π) ), 1(cos⁡(\(\frac{3\pi}{2}\)) + i sin⁡(\(\frac{3\pi}{2}\)) ).

Exercise 3.
Find the sixth roots of unity in rectangular form by creating and solving a polynomial equation. Show work to support your answer. Find the sixth roots of unity in polar form.
Answer:
x⁶ – 1 = 0
(x³ + 1)(x³ – 1) = 0
(x + 1)(x² – x + 1)(x – 1)(x² + x + 1) = 0
By inspection, 1 and – 1 are sixth roots. Using the quadratic formula to find the solutions to x² – x + 1 = 0 and x² + x + 1 = 0 gives the other four roots: \(\frac{1}{2}\) + \(\frac{i \sqrt{3}}{2}\), \(\frac{1}{2}\) – \(\frac{i \sqrt{3}}{2}\), – \(\frac{1}{2}\) + \(\frac{i \sqrt{3}}{2}\), and – \(\frac{1}{2}\) – \(\frac{i \sqrt{3}}{2}\).
In polar form, 1(cos⁡(0) + i sin⁡(0) ), 1(cos⁡(\(\frac{\pi}{3}\)) + i sin⁡(\(\frac{\pi}{3}\)) ), (cos⁡(\(\frac{2\pi}{3}\)) + i sin⁡(\(\frac{2\pi}{3}\)) ), 1(cos⁡(π) + i sin⁡(π) ), 1(cos⁡(\(\frac{4\pi}{3}\)) + i sin⁡(\(\frac{4\pi}{3}\)) ), 1(cos⁡(\(\frac{5\pi}{3}\)) + i sin⁡(\(\frac{5\pi}{3}\)) ).

Exercise 4.
Without using a formula, what would be the polar forms of the fifth roots of unity? Explain using the geometric effect of multiplication complex numbers.
Answer:
The modulus would be 1 because dividing 1 into the product of six equal numbers still means each number must be 1. The arguments would be fifths of 2π, so 0, \(\frac{\pi}{5}\), \(\frac{2\pi}{5}\), \(3\frac{\pi}{5}\), and \(\frac{4\pi}{5}\). The fifth roots of z, when multiplied together, must equal z¹ = z^{\(\frac{1}{5}\)}∙z^{\(\frac{1}{5}\)}∙z^{\(\frac{1}{5}\)}∙z^{\(\frac{1}{5}\)}∙z^{\(\frac{1}{5}\)} . That would be like starting with the real number 1 and rotating it by \(\frac{1}{5}\) of 2π and dilating it by a factor of 1 so that you ended up back at the real number 1 after 5 repeated multiplications.

Discussion
What is the modulus of each root of unity regardless of the value of n? Explain how you know.
Answer:
The modulus is always 1 because the n^{th/sup> root of 1 is equal to 1. The points are on the unit circle, and the radius is always 1.}

How could you describe the location of the roots of unity in the complex plane?
Answer:
They are points on a unit circle, evenly spaced every \(\frac{2\pi}{n}\) units starting from 1 along the positive real axis.

The diagram below shows the solutions to the equation x³ = 27. How do these numbers compare to the cube roots of unity (e.g., the solutions to x³ = 1)?

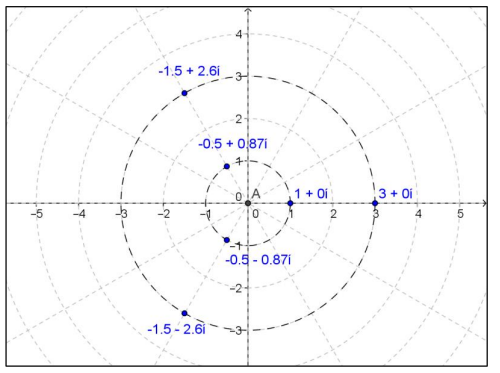
Answer:
They are points on a circle of radius 3 since the cube root of 27 is 3. Each one is a scalar multiple (by a factor of 3) of the cube roots of unity. Thus, they have the same arguments but a different modulus.

Eureka Math Precalculus Module 3 Lesson 3 Problem Set Answer Key

Question 1.
Graph the n^th roots of unity in the complex plane for the specified value of n.
a. n = 3
Answer:

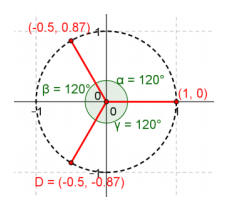
b. n = 4
Answer:

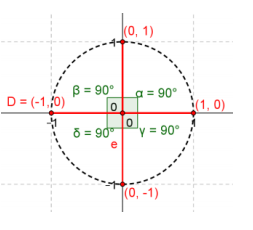
c. n = 5
Answer:

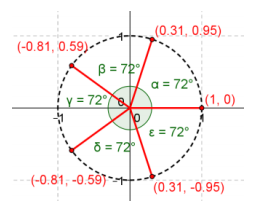
d. n = 6
Answer:

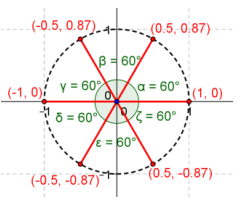
Question 2.
Find the cube roots of unity by using each method stated.
a. Solve the polynomial equation x³ = 1 algebraically.
Answer:
x³ – 1 = 0, (x – 1)(x² + x + 1) = 0, x = 1, x² + x + 1 = 0, x = \(\frac{ – 1 \pm \sqrt{1 – 4}}{2}\) = – \(\frac{1}{2}\)±\(\frac{\sqrt{3} i}{2}\)
The roots of unity are 1, – \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i, – \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i.

b. Use the polar form z³ = r(cos⁡(θ) + sin⁡(θ) ), and find the modulus and argument of z.
Answer:
z³ = 1, r³ = 1, r = 1
3θ = 0, 3θ = 2π, 3θ = 4π, …; therefore, θ = 0, \(\frac{2\pi}{3}\), \(\frac{4\pi}{3}\), 2π, …
z = \(\sqrt[3]{r}\)(cos⁡(θ) + i sin⁡(θ) )
z₁ = 1(cos⁡(0) + i sin⁡(0) ) = 1
z₂ = 1(cos⁡(\(\frac{2\pi}{3}\)) + i sin⁡(\(\frac{2\pi}{3}\)) ) = – \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i
z₃ = 1(cos⁡(\(\frac{4\pi}{3}\)) + i sin⁡(\(\frac{4\pi}{3}\)) ) = – \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i
The roots of unity are 1, – \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i, – \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i.

c. Solve (a + bi)³ = 1 by expanding (a + bi)³ and setting it equal to 1 + 0i.
Answer:
(a + bi)³ = 1, a³ + 3a² bi – 3ab² – b³ i = 1; therefore, a³ – 3ab² = 1 and 3a² b – b³ = 0.
For 3a² b – b³ = 0, b(3a² – b² ) = 0, we have either b = 0 or a² – b² = 0.
For b = 0, we substitute it in a³ – 3ab² = 1, a³ = 1, a = 1; therefore, we have 1 + 0i.
For 3a² – b² = 0, b² = 3a², we substitute it in a³ – 3ab² = 1, a³ – 9a³ = 1, a³ = – \(\frac{1}{8}\), a = – \(\frac{1}{2}\).
For = – \(\frac{1}{2}\), we substitute it in b² = 3a², and we get b = ±\(\frac{\sqrt{3}}{2}\). Therefore, we have \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i and \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i.
The roots of unity are 1, – \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i, – \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i.

Question 3.
Find the fourth roots of unity by using the method stated.
a. Solve the polynomial equation x⁴ = 1 algebraically.
Answer:
x⁴ – 1 = 0, (x² + 1)(x + 1)(x – 1) = 0, x = ±i, x = ±1
The roots of unity are 1, i, – 1, – i.

b. Use the polar form z⁴ = r(cos⁡(θ) + sin⁡(θ) ), and find the modulus and argument of z.
Answer:
z⁴ = 1, r⁴ = 1, r = 1
4θ = 0, 4θ = 2π, 4θ = 4π, 4θ = 6π, 4θ = 8π, …; therefore, θ = 0, \(\frac{\pi}{2}\), π, \(\frac{3\pi}{2}\), 2π, …
z = \(\sqrt[3]{r}\)(cos⁡(θ) + i sin⁡(θ) )
z₁ = 1(cos⁡(0) + i sin⁡(0) ) = 1
z₂ = 1(cos⁡(\(\frac{\pi}{2}\)) + i sin⁡(\(\frac{\pi}{2}\))) = i
z₃ = 1(cos⁡(π) + i sin⁡(π) ) = – 1
z₄ = 1(cos⁡(\(\frac{3\pi}{2}\)) + i sin⁡(\(\frac{3\pi}{2}\))) = – i
The roots of unity are 1, i, – 1, – i.

c. Solve (a + bi)⁴ = 1 by expanding (a + bi)⁴ and setting it equal to 1 + 0i.
Answer:
(a + bi)⁴ = 1, a⁴ + 4a³ bi – 6a² b² – 4ab³ i + b⁴ = 1.
Therefore, a⁴ – 6a² b² + b⁴ = 1 and 4a³ b – 4ab³ = 0.
For 4a³ b – 4ab³ = 0, 4ab(a² – b² ) = 0, we have either a = 0, b = 0, or a² – b² = 0.
For a = 0, we substitute it in a⁴ – 6a² b² + b⁴ = 1, b⁴ = 1, b = ±1; therefore, we have fourth roots of unity i and – i.
For b = 0, we substitute it in a⁴ – 6a² b² + b⁴ = 1, a⁴ = 1, a = ±1 for a. b∈R; therefore, we have fourth roots of unity 1 and – 1.
For a² – b² = 0, a² = b², we substitute it in a⁴ – 6a² b² + b⁴ = 1, b⁴ – 6b⁴ + b⁴ = 1, 4b⁴ = – 1; there is no solution for b for a. b∈R;
The roots of unity are 1, i, – 1, – i.

Question 4.
Find the fifth roots of unity by using the method stated.
Use the polar form z⁵ = r(cos⁡(θ) + sin⁡(θ) ), and find the modulus and argument of z.
Answer:
z⁵ = 1, r⁵ = 1, r = 1
5θ = 0, 5θ = 2π, 5θ = 4π, 5θ = 6π, 5θ = 8π, 5θ = 10π, …; therefore, θ = 0, \(\frac{2\pi}{5}\), \(\frac{4\pi}{5}\), \(\frac{6\pi}{5}\), \(\frac{8\pi}{5}\), 2π, …
z₁ = 1(cos⁡(0) + i sin⁡(0) ) = 1
z₂ = 1(cos(⁡\(\frac{2\pi}{5}\)) + i sin⁡(\(\frac{2\pi}{5}\)) ) = 0.309 + 0.951i
z₃ = 1(cos⁡(\(\frac{4\pi}{5}\)) + i sin⁡(\(\frac{4\pi}{5}\)) ) = – 0.809 + 0.588i
z₄ = 1(cos⁡(\(\frac{6\pi}{5}\)) + i sin⁡(\(\frac{6\pi}{5}\)) ) = – 0.809 – 0.588i
z₅ = 1(cos⁡(\(\frac{8\pi}{5}\)) + i sin⁡(\(\frac{8\pi}{5}\)) ) = 0.309 – 0.951i
The roots of unity are 1, 0.309 + 0.951i, – 0.809 + 0.588i, – 0.809 – 0.588i, 0.309 – 0.951i, 1.

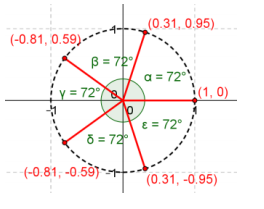
Question 5.
Find the sixth roots of unity by using the method stated.
a. Solve the polynomial equation x⁶ = 1 algebraically.
Answer:
x⁶ – 1 = 0, (x + 1)(x² – x + 1)(x – 1)(x² + x + 1) = 0, x = ±1, x = \(\frac{1}{2}\) ±\(\frac{\sqrt{3} i}{2}\), x = – \(\frac{1}{2}\) ±\(\frac{\sqrt{3} i}{2}\)
The roots of unity are 1, – 1, \(\frac{1}{2}\) + \(\frac{\sqrt{3} i}{2}\), \(\frac{1}{2}\) – \(\frac{\sqrt{3} i}{2}\), – \(\frac{1}{2}\) + \(\frac{\sqrt{3} i}{2}\), – \(\frac{1}{2}\) – \(\frac{\sqrt{3} i}{2}\).

b. Use the polar form z⁶ = r(cos⁡(θ) + sin⁡(θ) ), and find the modulus and argument of z.
Answer:
z⁶ = 1, r⁶ = 1, r = 1
6θ = 0, 6θ = 2π, 6θ = 4π, 6θ = 6π, 6θ = 8π, 6θ = 10π, 6θ = 12π, 6θ = 14π, …; therefore, θ = 0, \(\frac{\pi}{3}\), \(\frac{2}{3}\), π, \(\frac{4\pi}{3}\), \(\frac{5\pi}{3}\), 2π, \(\frac{7\pi}{3}\), …
z₁ = 1(cos⁡(0) + i sin⁡(0) ) = 1
z₂ = 1(cos⁡(\(\frac{\pi}{3}\)) + i sin⁡(\(\frac{\pi}{3}\)) ) = \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i
z₃ = 1(cos⁡(\(\frac{2\pi}{3}\)) + i sin⁡(\(\frac{2\pi}{3}\)) ) = – \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i
z₄ = 1(cos⁡(π) + i sin⁡(π) ) = – 1
z₅ = 1(cos⁡(\(\frac{4\pi}{3}\)) + i sin⁡(\(\frac{4\pi}{3}\)) ) = – \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i
z₆ = 1(cos⁡(\(\frac{5\pi}{3}\)) + i sin⁡(\(\frac{5\pi}{3}\)) ) = \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i
The roots of unity are 1, \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i, – \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i, – 1, – \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{2}\) i, \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) i.

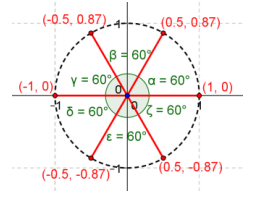
Question 6.
Consider the equation x^N = 1 where N is a positive whole number.
a. For which value of N does x^N = 1 have only one solution?
Answer:
N = 1

b. For which value of N does x^N = 1 have only ±1 as solutions?
Answer:
N = 2

c. For which value of N does x^N = 1 have only ±1 and ±i as solutions?
Answer:
N = 4

d. For which values of N does x^N = 1 have ±1 as solutions?
Answer:
Any even number N produces solutions ±1.

Question 7.
Find the equation that has the following solutions.
a.

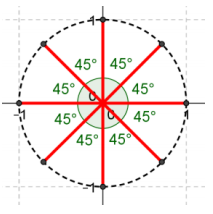
Answer:
x⁸ = 1

b.

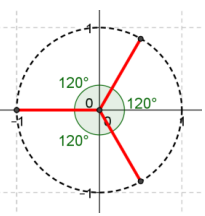
Answer:
x³ = – 1

c.

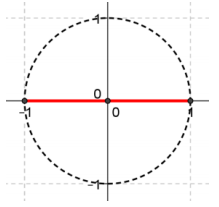
Answer:
x² = 1

Question 8.
Find the equation (a + bi)^N = c that has solutions shown in the graph below.

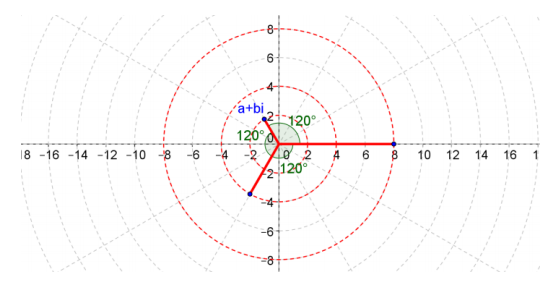
Answer:
( – 1 + \(\sqrt{3}\)i)³ = 8

Eureka Math Precalculus Module 3 Lesson 3 Exit Ticket Answer Key

Question 1.
What is a fourth root of unity? How many fourth roots of unity are there? Explain how you know.
Answer:
The fourth root of unity is a number that multiplied by itself 4 times is equal to 1. There are 4 fourth roots of unity. x⁴ = 1 results in solving the polynomial x⁴ – 1 = 0. The fundamental theorem of algebra guarantees four roots since that is the degree of the polynomial.

Question 2.
Find the polar form of the fourth roots of unity.
Answer:
For the fourth roots of unity, n = 4 and r = 1, so each root has modulus 1, and the arguments are 0, \(\frac{2\pi}{4}\), \(\frac{4\pi}{4}\), and \(\frac{6\pi}{4}\). We can rewrite the arguments as 0, \(\frac{\pi}{2}\), π, and \(\frac{3\pi}{2}\). Then, the fourth roots of unity are
x₁ = cos⁡(0) + i sin⁡(0) = 1
x₂ = cos⁡(\(\frac{\pi}{2}\)) + i sin⁡(\(\frac{\pi}{2}\)) = i
x₃ = cos⁡(π) + i sin⁡(π) = – 1
x₄ = cos⁡(\(\frac{3\pi}{2}\)) + i sin⁡(\(\frac{3\pi}{2}\)) = – i.

Question 3.
Write x⁴ – 1 as a product of linear factors, and explain how this expression supports your answers to Problems 1 and 2.
Answer:
Since there are four roots of unity, there should be four linear factors.
x⁴ – 1 = (x – 1)(x – i)(x + 1)(x + i)